基于坐标旋转的天线系统标校技术
2019-04-24耿大孝张振庄
耿大孝,张振庄
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
随着卫星通信的发展,卫星地球站的种类越来越多,不仅有固定站,还有车载、船载和机载站,配套的天线座架形式也多种多样,常见的如A-E,A-E-C,A-C-E,X-Y-Z等不同类型。为了实现卫通天线对目标的高精度指向跟踪,需要在惯导或其他测量设备提供的天线基础平面的姿态和位置信息引导下实现天线的大地指向的精确测量和控制,从而对不同座架型式的天线提出了系统标校的要求。
已有的天线系统标校主要应用于A-E两轴座架的大口径测控天线[1],标校采用基于球面三角几何推导得出的近似公式,无法推广应用在其他座架的天线系统标校中。而且该方法需要天线通过经纬仪、应答机等标校仪器对准几何关系精确确定的方位标、校准塔等标校设施,这些条件在很多应用场合是无法实现的,因此需要开发新的适用范围广的标校方法,实现不同座架形式的天线系统误差的标校。
1 坐标旋转法推导标校公式
天线主要的系统误差[1]有以下3种:
① 座架基础轴旋转平面相对于天线安装基础平面的不平行度,如A-E座架的方位转盘的大盘不水平度和不水平角;
② 座架各机械轴的机械零点和各机械轴的相对关系误差,如A-E座架的方位、俯仰零点和两轴的不正交度;
③ 座架的机械轴与天线电轴的不重合角,如A-E座架的方位、俯仰2个轴向的光电误差。
天线系统标校的核心思想是通过几何测量和数学计算得出天线相对于基准面的高精度指向角计算值作为真值来标校天线系统误差,因此标校公式的形式是以各系统误差作为系数、天线座架各轴实测角的计算值作为变量的多项式,多项式等于真值和实测角计算值的差值。
坐标旋转法[2]推导标校公式就是采用坐标旋转的方法推导出天线指向的标校公式,该方法是在已经确定天线的大地角和天线基准面的姿态角的前提下,应用欧拉旋转方法将天线坐标系的单位指向向量经大地坐标系旋转至天线基准面坐标系,确定标校的基准值,再将天线单位指向向量经各系统误差及座架各轴实测角旋转矩阵旋转至天线基准面坐标系,经近似计算后转化为各系统误差作为系数、天线座架各轴实测角的计算值作为变量的多项式,将从2个路径旋转后的在基准面坐标系下表征天线单位指向向量的三维坐标分别相等,即得出坐标旋转法推导出的3个天线系统标校公式。
1.1 坐标系
坐标旋转法推导天线系统标校公式所用的坐标系[3]分别说明如下:
① 天线坐标系(Oa—XaYaZa)
原点Oa在天线中心,OaYa轴与天线电轴重合,OaZa轴在天线平面内指向天线面的最高点,OaXa轴由右手定则确定。
② 地理(惯性)坐标系(Og—XgYgZg)
由于大地坐标系是移动载体惯性导航器件的测量基准平面,因此又称为惯性坐标系。
原点Og在天线所在地理位置,OgYg轴平行于大地平面指向正北,OgZg轴沿天线所在地点的铅垂线向上指向天顶,OgXg轴在大地平面内指向正东。
③ 基准面(甲板)坐标系(Oj—XjYjZj)
船载天线安装在船甲板平面,因此又称甲板坐标系。
原点Oj在天线所在基准平面位置,OjYj轴平行于基准平面指向首端(如船甲板的船艏),OjZj轴平行于基准面法线(如船甲板的船桅)向上,OjXj轴由右手定则确定。
由于坐标系之间没有相对位移,各坐标系的原点都是天线中心的空间位置,在后面的叙述中统一表示为‘O’,只需要旋转即可完成相互转换。
1.2 数学模型建立
现在通过坐标旋转方法推导船载A-E-C三轴座架卫星通信天线的系统标校计算公式,并以该型座架的系统标校结果来验证标校计算公式及方法的有效性。
天线对准目标后,天线电轴指向由天线中心指向目标卫星,不考虑连线的长度,用单位向量表示天线指向,在天线坐标系中表示为:

(1)
天线坐标先由天线坐标系(Oa—XaYaZa)旋转至大地坐标系(Og—XgYgZg),旋转角[4]依次为俯仰地理角Eg和方位地理角Ag,旋转过程如图1所示。

图1 天线坐标到地理坐标旋转示意图
由图可得,俯仰地理角旋转矩MEg为:
(2a)
方位地理角旋转矩阵MAg为:
(2b)
天线坐标系旋转至大地坐标系(Og—XgYgZg)后,再旋转至甲板坐标系(Oj—XjYjZj),旋转角依次为航向角k、纵倾角p、横摇角r,旋转示意如图2所示。

图2 惯导坐标到甲板坐标旋转示意图
由图可得,航向旋转矩阵Mk为:
(3a)
纵摇旋转矩阵Mp为:
(3b)
横摇旋转矩阵为:
(3c)
天线单位指向向量在天线坐标系中的坐标依次左乘各矩阵后得出其在甲板坐标系中坐标,该坐标作为系统标校的真值。
天线坐标系另一转换路径为经系统误差和A-E-C座架各轴角度的矩阵旋转至甲板坐标系。
A-E-C三轴座架由3个依次正交的旋转轴组成,从上到下分别为交叉轴、俯仰轴、方位轴,天线安装在交叉轴上。座架示意图如图3所示。
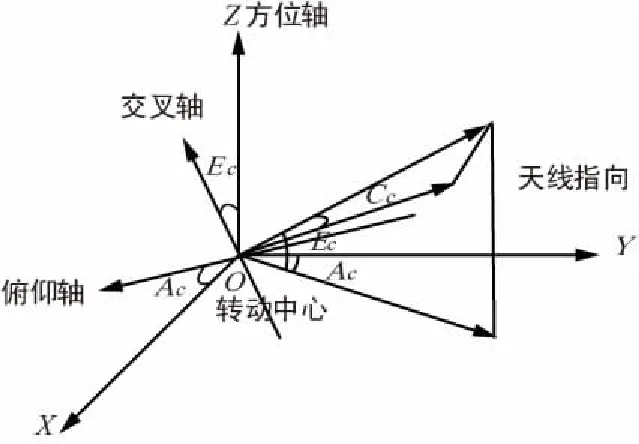
图3 A-E-C三轴座架示意图
交叉轴编码角Cc为天线指向矢量与俯仰转动平面的夹角,俯仰轴编码角Ec为天线指向矢量在俯仰转动平面的投影与方位转盘的夹角,方位轴编码角Ac为天线指向矢量在俯仰转动平面的投影在方位转盘的二次投影与甲板首尾线的夹角。该型座架天线的从上倒下排列的系统误差如表1所示。
表1 A-E-C座架天线系统误差表
由天线坐标系经天线座架至甲板坐标系分4步走,各步旋转进行分别说明。
第1步由天线坐标系(Oa—XaYaZa)旋转至过渡的交叉轴坐标系(O—XCcYCcZCc),旋转角依次为Ce,Cs,Cc,旋转示意如图4所示。
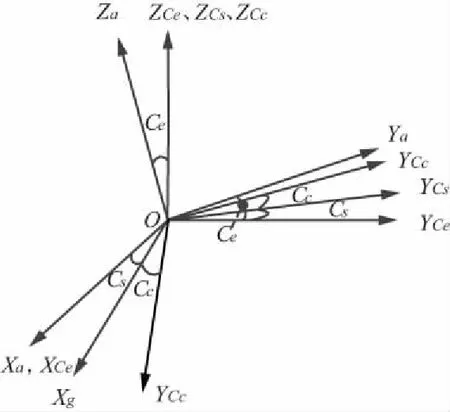
图4 天线坐标至交叉坐标旋转示意图
由图可知,俯仰轴机电误差Ce旋转矩阵MCe为:
(4a)
交叉轴机电误差Cs旋转矩阵MCs为:
(4b)
交叉轴实测转角Cc旋转矩阵MCc为:
(4c)
第2步由交叉轴坐标系(O—XCcYCcZCc)旋转至过渡的俯仰轴坐标系(O—XEcYEcZEc),旋转角依次为δn,E0,Ec,旋转示意如图5所示。
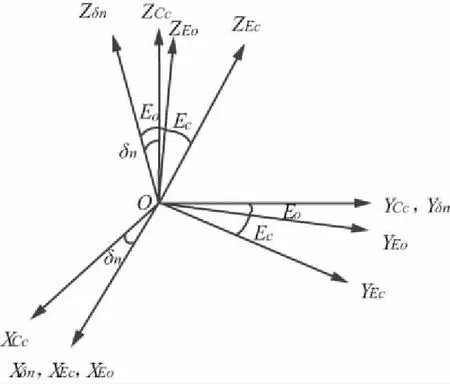
图5 交叉坐标至俯仰坐标旋转示意图
由图5可知,俯仰交叉不正交误差δn旋转矩阵Mδn为:
(5a)
俯仰零度误差E0旋转矩阵MEo为:
(5b)
俯仰轴实测转角Ec旋转矩阵MEc为:
(5c)
第3步由俯仰轴坐标系(O—XEcYEcZEc)旋转至过渡的方位轴坐标系(O—XAcYAcZAc),旋转角依次为δm,A0,Ac,旋转示意如图6所示。
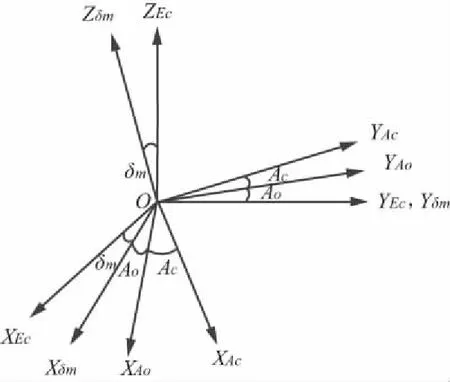
图6 俯仰坐标系至方位坐标系旋转示意图
由图6可知,方位轴俯仰轴不正交度δm旋转矩阵Mδm为:
(6a)
方位零度误差A0旋转矩阵MA0为:
(6b)
方位轴实测角Ac旋转矩阵MAc为:
(6c)
第4步由方位轴坐标系(O—XAcYAcZAc)旋转至甲板坐标系(O—XjYjZj),旋转角依次为δr,δp,旋转示意如图7所示。

图7 方位坐标系至甲板坐标系旋转示意图
由图7可知,方位转盘横倾误差δr旋转矩阵Mδr为:
(7a)
方位转盘纵倾误差δp旋转矩阵Mδp为:
(7b)
最终矩阵等式[5]为:
(8)
由于系统误差弧度的绝对值很小,因此矩阵等式运算可以进行以下近似处理:
① 系统误差的正弦值近似为系统误差的弧度值;
② 系统误差的余弦近似为1;
③ 系统误差的近似处理后的弧度值的乘积近似为0。
计算结果为天线单位指向向量在甲板坐标系的坐标等式,是以天线系统误差为系数的多项式,见式(9a),(9b),(9c)。
(9a)
(9b)
(9c)
采用最小二乘法[6-7],结合(9a),(9b),(9c)三个等式,标定出A-E-C座架天线的各项系统误差。
2 应用分析
2.1 仿真计算
采用matlab工具[8],编程仿真运算验证基于坐标旋转推导出的船载A-E-C座架天线的系统标校数学模型的正确性。
设定一组系统误差值,设置方位、俯仰及交叉轴实测角大范围等间隔同步变化,把系统误差和各轴实测角通过坐标转换方式得出的天线指向坐标作为真值,代入公式,采用最小二乘法标定出各系统误差项,标定结果如表2所示,指向修正误差比较结果如表3所示。

表2 天线系统标校仿真结果表 (′)

表3 仿真标校指向修正结果表 (′)
由表2和表3可见,该标校方法仿真标校出的系统误差对指向修正作用明显。
2.2 动态验证
通过船载1.5 m Ka频段A-E-C三轴天线摇摆台动态跟踪[9]试验来验证该方法的正确性。
试验内容及步骤如下:
① 先确定天线和目标卫星的经度、纬度和高度,并精确天线对星的精确地理指向;
② 天线安装在三轴摇摆台上,摇摆台同时安装有高精度惯导作为引导装置;
③ 天线采用单脉冲跟踪方式跟踪目标卫星,摇摆台各轴大范围长周期摇摆;
④ 以0.1 s间隔记录保存多个摇摆周期的天线座架各轴实测角和惯导测出的姿态角;
⑤ 换目标卫星重复步骤①~④。
编写matlab程序[10],引用各目标卫星跟踪数据记录文件标定天线系统误差,将修正前和修正后地理指向角按excel格式保存到同一个文件中,并形成与精确地理指向角的方位和俯仰差值数据[11]。修正前的方位和俯仰差散点图如图8所示,修正后如图9所示。

图8 修正前的误差图
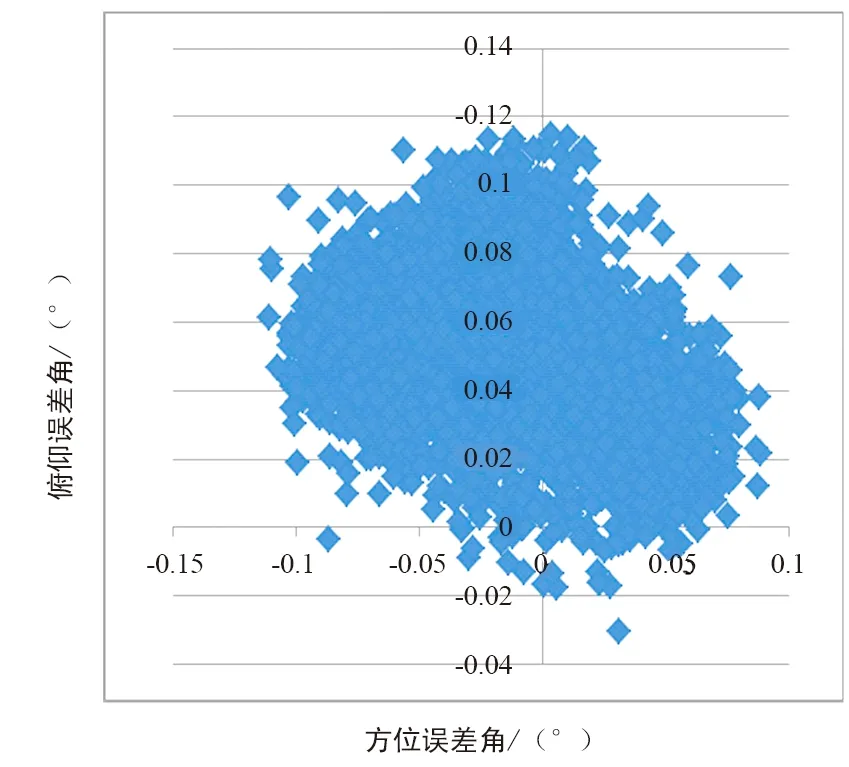
图9 修正后的误差图
比较图8和图9,采用系统误差修正后的指向角明显比未修正的指向更趋近于真实指向。
2.3 实际应用
某大型船载A-E-C座架卫通天线具有船载惯导引导的指向跟踪功能,由于在前期没有进行系统标校,天线的指向跟踪误差较大,即使在船摇较小的情况下也会出现卫星通信中断现象。
采用该方法标定出系统误差,并通过坐标转换实时修正天线指向后,即使船摇较大,天线的指向跟踪依然能够保证卫星通信的连续。
3 结束语
针对特定座架类型天线,通过坐标旋转推导出包含系统误差计算公式,作为该型座架天线的系统标校数学模型,适用于绝大多数天线。除了A-E-C座架天线,还对A-E,A-C-E等座架天线进行了公式推导、静态仿真和动态验证,证明该方法真实有效。
但由于标校计算公式是通过近似运算得出,因此要求待标定系统误差绝对值很小,这样可通过高效的标定方法获取尽可能大范围均匀变化的各轴测量角以及其对应的基准角,完成精确的天线系统标校。
