基于复合赋权TOPSIS的雷达工作模式识别
2019-04-23唐玉文何明浩程柏林
唐玉文,何明浩,韩 俊,程柏林
(空军预警学院,武汉 430019)
0 引 言
当前雷达的多功能趋势越来越明显,一部多功能雷达常常具备多种工作模式。不同的工作模式对应不同的战术任务,也就意味着不同的威胁等级。
对于自卫电子对抗方而言,一旦敌方雷达进入跟踪状态,就意味着面临巨大的威胁,雷达告警器必须做出及时准确的告警;另一方面,自动识别敌方雷达工作模式也是实现认知电子战的重要基础。在作战过程中,只有实时根据所需对抗雷达的威胁程度来进行干扰资源分配才能最大限度地发挥电子对抗系统的作战效能[1-2]。通过对敌方雷达工作模式的识别可以实现威胁等级判别和辅助干扰样式选择[3],这样可以有效防止干扰资源的浪费,提升干扰的针对性和有效性。因此,开展雷达工作模式识别具有重要意义。
当前,雷达工作模式识别主要依靠人工经验进行分析,这种做法对于事后情报整编具有一定价值。但是,对于雷达告警和威胁评估等需要实时给出分析结果以及面临海量数据时的应用场景,人工分析将难以应对。因此,亟需开展雷达工作模式识别算法研究。
本文将雷达工作模式识别问题转化为一类多属性决策问题。引入模糊集中的隶属度函数建立决策矩阵,然后综合采用主观赋权法中的AHP权值与客观赋权法中的熵权值得到各属性的复合权值,最后利用多属性决策中的逼近理想解的排序方法(Technique for Order Preference by Similarity to Ideal Solution, TOPSIS)进行工作模式识别。仿真结果验证了本文方法的有效性。
1 TOPSIS多属性决策方法
TOPSIS是Hwang等人于1981年提出的一种多属性决策方法,该方法构造了n维属性空间的正负理想点,通过求解各方案与正负理想点之间的欧式距离来对方案进行排序[4]。其具体计算步骤如下[5-6]:
设M={M1,M2,…,Mm}为某一多属性决策问题的备选方案集,X={X1,X2,…,Xn}为方案的属性集,对于任一方案Mi(i=1,2,…m)其属性值构成的向量为Xi=[xi1,xi2,…,xin]。
Step1:根据每个方案的属性值构建决策矩阵R如表1所示。

表1 决策矩阵
Step2:为消除不同指标之间量纲与量级的影响,对R进行规范化处理得到规范化决策矩阵Y=[yij]m×n,即
(1)

zij=wj·yij,i=1,…,m;j=1,…,n
(2)
(3)
(4)
式中:J+表示效益型属性集,即属性值越大方案越优;J-表示成本型属性集,即属性值越小方案越优。
(5)
Step6:计算各备选方案的综合评价指数
(6)
显然,式中Ci∈[0,1],其值大小代表了备选方案的相对优劣程度。Ci值越大说明备选方案离正理想点越近,离负理想点越远,方案越好,反之亦然。
2 复合赋权方法
对于多属性决策而言,权值的合理性直接影响决策的正确率。常用的赋权方法主要有两类:一类是基于人工经验设定权值的主观赋权法,典型的有层次分析法[7](Analytic Hierarchy Process, AHP)、专家打分法[8]等。这类赋权方法完全依赖于决策者的偏好和经验,准确性和一致性较差;另一类是基于指标参数数值分布情况确定权值的客观赋权方法,典型的有熵权法[9]、主成分分析法[10-11]等。这类赋权方法完全依赖数据本身,有时不能很好的体现识别对象的特点。因此,本文将主观赋权法中的层次分析法与客观赋权法中的熵权法相结合形成复合赋权方法以提高赋权的可靠性。
2.1 AHP权值计算
层次分析法是美国运筹学家T.L.Saaty于20世纪70年代提出的分析方法,它吸收和利用了行为科学的特点,对决策者的经验判断给予量化,是一种有效的主观赋权方法[12]。假设n个指标的AHP权值向量为WAHP=[w1,w2,…,wn],则求解AHP权值的具体做法是[13-14]:
Step1:由决策人对各指标的重要性进行两两比较,并把第i个指标对第j个指标的相对重要性记为aij。根据n个指标成对比较的结果得到比较矩阵
(7)
Setp2:将比较矩阵A中每行元素连乘并开n次方得到
(8)
Setp3:求解各个指标的权值
(9)
Setp4:对矩阵A中每列元素求和
(10)
Setp5:计算λmax的值
(11)


表2 一致性检验的指标
2.2 熵权值计算
熵权法是一种根据各项指标观测值所提供的信息量的大小来确定目标权重的方法[15]。它概念清晰、计算简单,因此本文选用熵权作为客观权值的来源。它的定义如下[16]:
定义1(指标的熵):在有m个备选方案,n个指标的决策问题中(以下简称(m,n)决策问题),第j个指标的熵值Hj定义为
(12)

定义2(指标的熵权):在(m,n)决策问题中,第j个指标的熵权值wj定义为
(13)
根据式(12)和(13)就可以计算得到指标的熵权向量WH=[w1,w2,…,wn]。
2.3 复合权值计算
由前述可知,不管是主观赋权法还是客观赋权法都存在一定的不足,因此很有可能出现所赋的权值与实际需求不相符的情况,这样就会导致整体识别率的大幅降低。为了提高赋权的可靠性,本文采用线性组合的方式将AHP权与熵权融合得到复合权值
W=(1-α)·WAHP+α·WH
(14)
式中:WAHP表示由AHP法得到的权值向量,WH为熵权法得到的权值向量,α为比例因子,用于调节主客观权值的比重。实际中,比例因子α需要根据数据信息的完整性和可信度以及对专家的信任程度,并结合具体识别对象来最终确定。
3 复合权值TOPSIS雷达工作模式识别算法
基于复合赋权TOPSIS的雷达工作模式识别算法,本质上是一种多属性决策方法,其前提和基础就是建立决策矩阵。对于工作模式识别而言,建立决策矩阵最直接的方法就是计算待识别脉冲串与雷达数据库中各备选雷达工作模式参数的匹配程度。因此,本文引入模糊集中的隶属度函数用于衡量待识别脉冲串与备选雷达工作模式参数的匹配程度。

Pk=[fk,τk,PRIk,MOPk]
(15)
根据已知雷达工作模式Mi的参数和待识别雷达脉冲串S的参数,就可以建立隶属度函数。但不同类型的参数需要使用不同的隶属度计算方法。以载频为例,当已知雷达工作模式Mi为载频固定时,第k个脉冲与工作模式Mi在载频上的隶属为
(16)
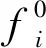
(17)
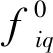
(18)


(19)
利用式(16)~(19)对脉冲串中的每个脉冲均进行隶属度计算后,再对所有脉冲在第j维参数上的隶属度求均值,就可以得到脉冲串S与第i个备选工作模式Mi在该维参数上的整体相似程度
(20)
式中:i=1,2,…,m;j=1,2,…,n。由此,通过隶属度函数的计算就可以得到一个m×n的隶属度矩阵,即决策矩阵
(21)
根据该决策矩阵,再利用复合赋权方法得到权值向量W,最后再由TOPSIS算法就可以实现对侦收雷达信号工作模式的识别。
4 仿真结果与分析
为检验基于复合权值TOPSIS雷达工作模式识别方法的有效性,本节通过一个计算实例和一个对比实验检验所提方法的识别效果。
4.1 算例分析
本文选用载频、脉宽、PRI和脉内调制样式作为识别参数,并以数字0,1,2,3分别表示单载频,线性调频,相位编码和频率编码的脉内调制样式。从雷达数据库中挑选一部相控阵机载火控雷达,且该雷达包含6种不同的空-空工作模式,各个工作模式的参数如表3所示。
假设当雷达工作于TWS模式时,我方截获一串雷达脉冲信号。此时,运用复合权值TOPSIS进行雷达工作模式识别。
Step1:根据(16)~(19)计算待识别脉冲串与各个工作模式的参数隶属度,且当隶属度极小时(小于0.001),直接将其赋值为0。由此得到决策矩阵为

(22)
Step2:根据(1)式对原始决策矩阵R进行规范化得到规范化决策矩阵

表3 某机载火控雷达空-空工作模式的参数范围

(23)
Step3:计算复合权值。首先计算AHP权。根据专家经验,通过两两对比的方法得到比较矩阵

(24)
再利用式(11)计算得到比较矩阵A对应的最大实特征根为λmax=4.0486,与表2中列出的临界特征值相比可知,小于4阶阵的临界特征值4.07,通过一致性检验,此时对应的AHP权值向量为
WAHP=[0.078 0.125 0.491 0.306]
(25)
再将规范化决策矩阵Y带入式(12)和(13)计算得到熵权为
WH=[0.037 0.230 0.284 0.449]
(26)
取比例因子α=0.5,根据式(14)计算得到复合权值为
W=[0.057 0.178 0.387 0.378]
Step4:利用复合权值对规范化决策矩阵加权,得到加权规范化决策矩阵

(28)
显然,隶属度属于效益型指标,那么由式(3)和(4)可知,相应的正、负理想解为
(29)
Step5:根据式(5)分别计算6个备选工作模式到正、负理想解的欧氏距离
(30)
Step6:通过式(6)计算得到6种工作模式的综合评价指数为
C=[0 0.472 0.510 0.998 0.042 0.468]
(31)
根据评价指数越大备选方案越优的排序准则,显然第四种工作模式——TWS模式的评价指数最大,因此识别为TWS模式。识别结果正确。这说明,基于复合权值的TOPSIS方法能够有效进行雷达工作模式识别。
4.2 算法比较
实际侦察环境中,由于噪声等原因,雷达信号参数的测量存在一定的随机误差。为检验算法在噪声条件下的鲁棒性,设置雷达参数(调制样式除外)的相对测量误差大小以1%为步长变化到10%。并定义相对测量误差ε为误差的均方差值σE与参数平均值μvar之比,即
(32)
仿真条件依旧采用表3中的参数,每种误差条件下均进行1000次蒙特卡罗仿真,每次仿真产生的雷达工作模式均从表3所列举的6种工作模式中随机选取。
为便于对比,本文同时选用性能较为优异的SVM算法进行了识别测试。设置SVM的核函数为径向基(RBF)核函数,惩罚系数为2,核函数参数为1,训练集和测试集均为1000个脉冲样本。得到识别结果如图1所示。

图1 识别正确率随测量误差的变化曲线
从图1可以看出,当参数测量不存在误差时,两种算法的识别率均为100%。但是,随着误差的逐渐增大,SVM算法的识别正确率迅速下降,且当误差超过5%时,SVM算法的识别率就已经下降到了85%以下,而本文方法在随着测量误差逐渐增大到10%的过程中,识别正确率始终保持在90%以上。这说明,在有测量误差的条件下,采用复合权值的TOPSIS识别方法比采用SVM稳定性更好,识别率更高。并且,该方法计算简单,且不需要事先使用大量样本训练分类器,因此可以大幅节省运算时间。
不仅如此,由于复合权值综合考虑了主观权值与客观权值,因此赋权可靠性比仅采用单一赋权法更高。即使其中有一种权值设置不当也不会造成识别率的急剧下降。如图2所示,为由于专家经验不足导致的AHP权值设置不当时的识别率。
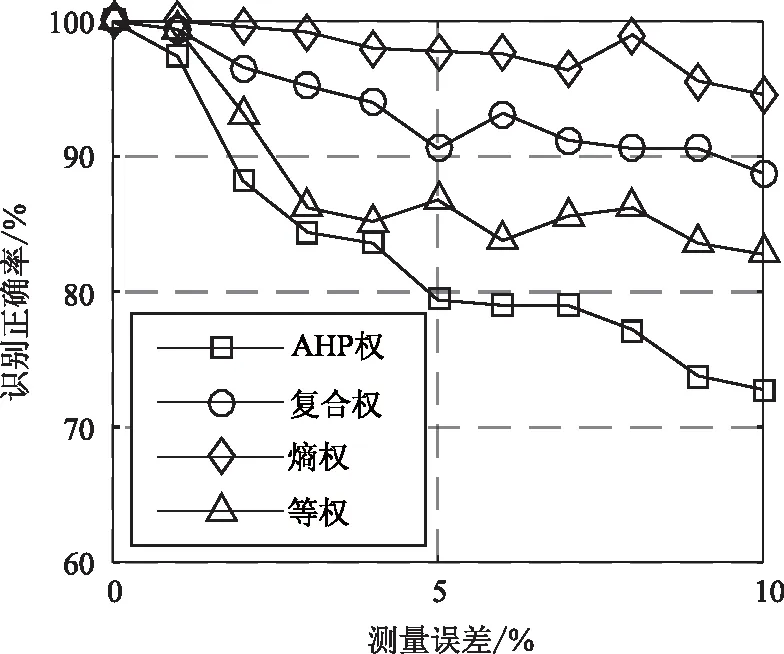
图2 AHP权赋值不当时的识别率

图3 熵权赋值不当时的识别率
从图中可以看出,此时如果仅使用AHP权,那么识别率会随着误差的增大而迅速下降,并且在相对误差为5%时识别率就已经跌落到80%以下。而基于复合权值的识别方法由于同时还融合了熵权,所以即使AHP权十分不合理,在相对测量误差达到9%的时候,其识别率依旧能保持在90%以上,并且识别率始终高于等权值法。类似的,当计算得出的熵权不合理时就会出现图3所示的情况。图中,采用熵权法的识别正确率随着误差增大下降迅速,并最终低于等权法。而采用复合权值法的识别率则相对稳定且始终较高。这说明,使用复合赋权方法可以有效增强TOPSIS算法权值计算的容错能力,提升识别算法的可靠性,防止因采用单一赋权法且赋权不当时,导致的识别率迅速下降的问题。另一方面,由于复合赋权是以牺牲一定的最高识别率为代价获取算法稳定度的,因此从图中也可以看出,该情况下复合赋权的识别率并不是最高的。但是,相比于赋权不当导致的识别率急剧下降,这种代价是可以接受的。
5 结 语
准确识别敌方雷达的工作模式对于威胁告警和电子对抗决策具有重要意义。本文将雷达工作模式识别问题转化为一类多属性决策问题,并引入决策理论中的TOPSIS方法进行识别。为雷达工作模式识别提供了一种新的研究思路。通过将熵权与AHP权融合提出了基于复合权值TOPSIS的雷达工作模式识别方法,提高了算法赋权的可靠性。仿真结果表明,该算法稳定性好,识别率较高,且在雷达参数测量存在误差的条件下优于SVM算法。可以为雷达告警器、电子情报(ELINT)侦察等多种应用场景提供参考。
