引入速率量测的高速机动目标跟踪多模型算法

石章松，刘 健，张渝缘

（海军工程大学电子工程学院，武汉 430033）

0 引言

现代海战中，水面舰艇面临的一个主要威胁就是反舰导弹。由于反舰导弹具有雷达反射截面积小、飞行速度快、突防能力强、爆炸威力大等特点，已被世界各国作为攻击水面舰艇的主要武器而积极进行发展和大量装备使用。目前，许多国家都在致力于研制新一代高速[3]（速度＞5 Ma）反舰导弹，对高速导弹的跟踪已逐渐成为热门话题。因此，如何提高对高速机动目标跟踪精度，是一个急需解决的问题。

由文献[4]知，引入参考加速度的跟踪算法对高速机动目标定位具有很高的精度，但当目标突然发生机动尤其是强机动时，其测量误差会大大增加，并且收敛速度较慢，达到稳定状态所需时间较长，有时甚至无法进行跟踪。

本文提出一种引入速率量测的三维自适应性圆周运动算法，当目标突然发生机动时，计算误差较小，收敛速度较快，到达稳定状态时间较短，但其对高速机动目标跟踪精度不高，误差较大。

因此，若将两种算法有效结合，既可以满足目标跟踪的精度需求，又可以满足算法对机动的及时反应需求。本文通过建立一种模型变换机制，将两种算法有效结合，从而满足高速机动目标快速精确跟踪需要，并通过仿真对比验证算法的有效性和可行性，为高速机动目标跟踪研究提供参考。

1 引入速率量测的VSMM算法

文中采用极坐标系下的量测模型和直角坐标系下的状态模型进行目标跟踪算法的研究。以跟踪器为原点建立空间坐标系，则目标在直角坐标系内的运动情况如图1所示：

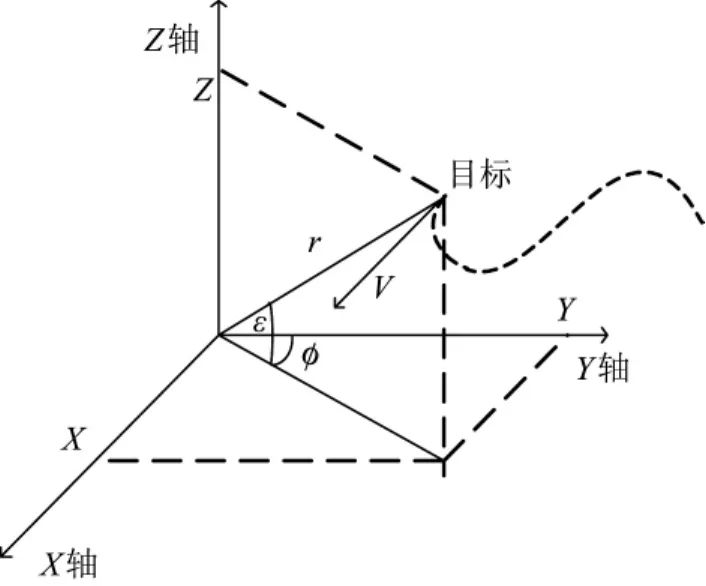
图1 目标运动模型

图中，r、φ、ε是跟踪器输出的斜距、方位角、俯仰角信息，其随机误差均方差分别为，是跟踪器输出的斜距、方位角、俯仰角的变化率信息，其随机误差均方差分别为，忽略系统误差。

则极坐标和直角坐标系的关系如下：

1.1 模型集合设计

通过对引入参考加速度的跟踪算法和三维自适应圆周运动算法进行比较，为了充分发挥两种算法的优点，在引入速率量测的情况下，设定两个模型集：

模型集1：引入参考加速度跟踪模型；CA跟踪模型[5]。

模型集2：三维自适应圆周运动模型。

通过引入合理的模型切换准则，可以将两种算法有效结合。

1.2 模型切换准则设计

本文采用平方检测法[6]，定义距离函数：

由新息序列的统计性质可知，D（k）服从自由度为m的x2分布。如果目标发生机动，新息d（k）将不再是均值为零的高斯白噪声过程，D（k）将会增大。因此，可以利用D（k）作为判别目标状态变化的依据。

1.3 VSMM算法流程

由于引入参考加速度的算法跟踪精度高，跟踪开始时通过模型集1对目标进行跟踪，当检测到机动发生时，即D（k）大于门限M1时，迅速切换到模型集2。因为模型集2此时计算误差小，稳定速度快。当模型集2到达稳定后，如果此时检测到D（k）小于门限M2，则可认为机动消除，由于在目标状态稳定条件下，模型集1跟踪精度高，此时将模型切换至模型1。具体流程如图2所示：

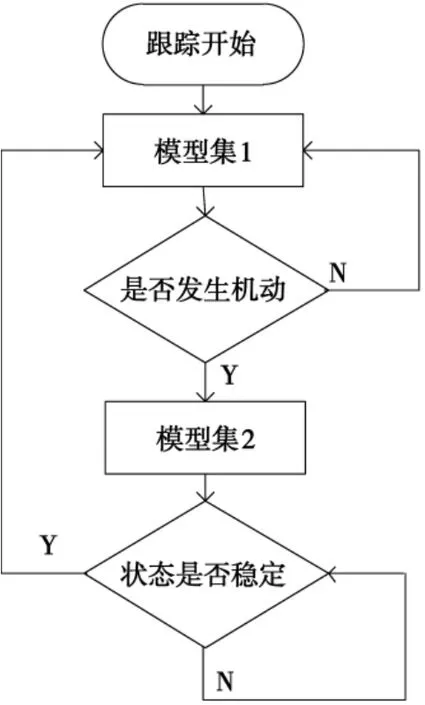
图2 VSMM算法流程

2 引入速率量测的模型设计

2.1 引入参考加速度的目标跟踪模型

考虑目标加速度服从以下四重一致混合分布[4]：

1）目标以参考加速度u（t）运动时概率为Pu；

2）无加速运动时概率为P0；

3）最大/小加速度amax/-amax运动时概率均为Pmax；

4）其他情况下相应加速度均匀分布在（amax，-amax）[7]。

加速度相应的均值和方差为：

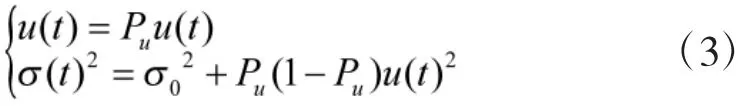
定义状态向量为：

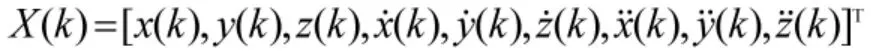
定义伪观测向量：

以X轴为例，假设参考加速度u（t）在相邻两个时刻间变化不剧烈，即：

则其状态方程：

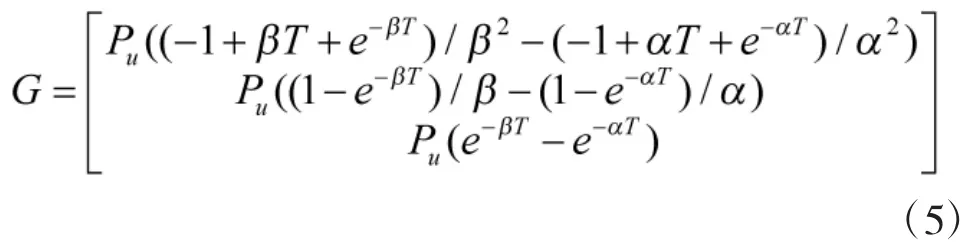
α为目标机动频率，β为参考加速度的变化强烈程度，β越小越强烈，通常，由于高速机动目标机动频率较小，取 α=1，β=1，对于 wk，其协方差矩阵为：

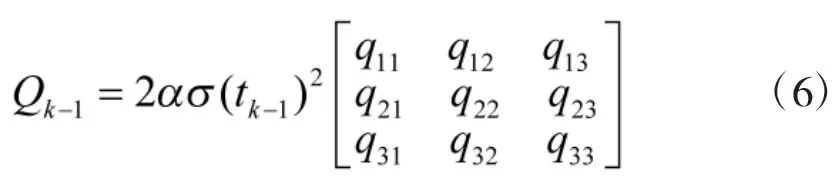
其中：

观测方程：

将跟踪器得到的球坐标系下的信息转换到直角坐标系下：

观测噪声V（k）是零均值、白色高斯过程噪声序列且相互独立，其协方差矩阵为：

其中系数矩阵A为：

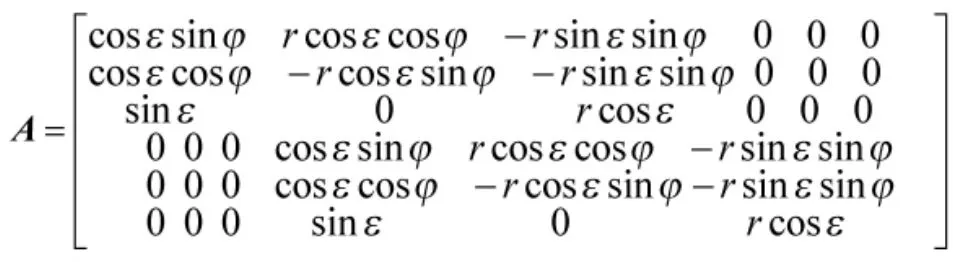
2.2 自适应三维圆周运动算法

由于引入速率量测，在角速率未知的情况下，将角速率作为状态方程的未知量带入计算，从而可以快速收敛求出角速率的近似值，因而满足机动发生时，角速率的自适应变换需要。

取卡尔曼非线性状态方程和线性观测方程中的各项为：

状态向量为：

其中，ω（1k），ω（2k）分别为目标方位角、高低角角速率。

伪观测向量为：

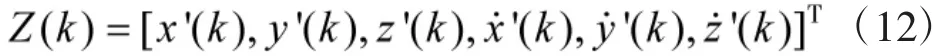
非线性状态方程为：

其中：

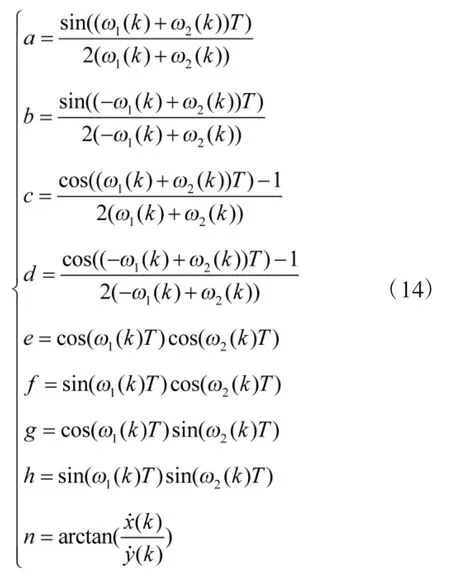
系统误差W（k）是零均值、白色高斯过程噪声序列，协方差为：

因为状态方程为非线性，因此，不再符合标准卡尔曼滤波的要求，考虑到无迹滤波相比于扩展卡尔曼滤波并没有近似非线性动态模型和量测模型，操作简单且精度较高[8-9]，这里选取无迹滤波的方法进行处理。

观测方程各项与上述引入参考加速度的算法相同。

3 仿真实现

为了验证文中所提算法的可行性和有效性，验证算法在高速机动目标和典型反舰导弹攻击航路态势[10]下跟踪精度相比于原来算法的效果，对算法进行蒙特卡洛仿真实现，并对滤波算法结果进行统计分析，从而比较各算法的跟踪性能。

3.1 高速机动目标情况

3.1.1 仿真参数设定

假设目标在水平面内运动，速度为2 000 m/s，作匀速直线运动，2 s后改为角速率为0.3 rad/s的匀速圆周运动，运动2 s后切换为角速度-0.2 rad/s的匀速圆周运动。跟踪器采样频率为100 Hz，跟踪时间共8 s；观测距离和观测距变率随机误差均方差10 m；观测方位角、高低角随机误差均方差5 mrad；观测方位角、高低角变化率随机误差均方差5 mrad/s，分别取 Pμ=0.5、P0=0.2、Pmax=0.1，加速度最大值 amax=10 m/s。

3.1.2 仿真结果

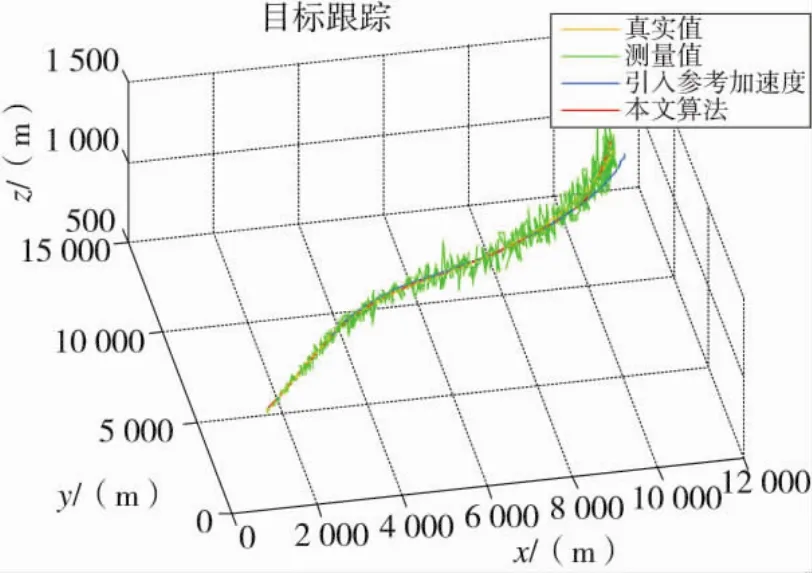
图3 目标运动轨迹及滤波效果模拟

具体各方向计算误差均方差对比如图4～图6所示。

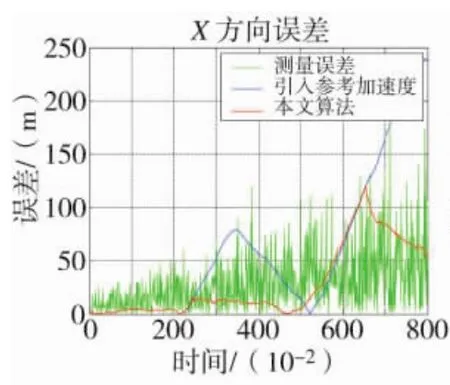
图4 X方向误差

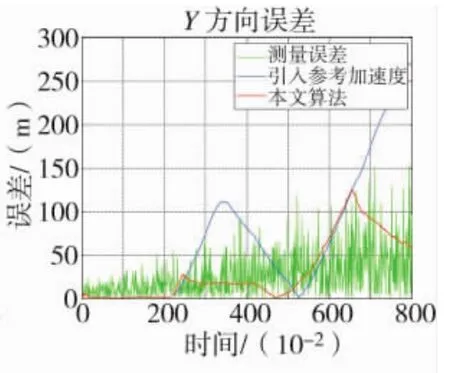
图5 Y方向误差

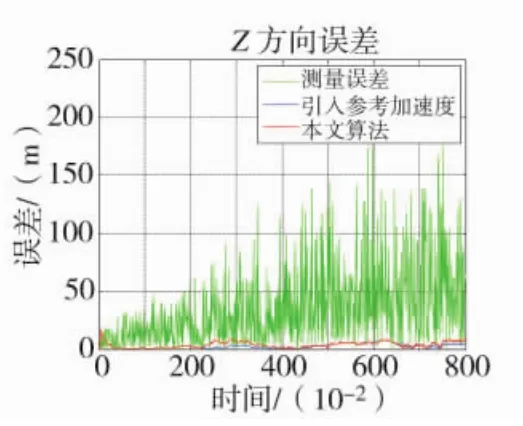
图6 Z方向误差

具体统计值如下页表1所示。

从图和表中可以看出，当目标发生机动时，引入参考加速度算法的误差会突然增大，收敛速度慢。而改进算法当目标发生机动时，其误差小，且收敛速度快，当目标状态稳定时，改进算法对目标跟踪精度高。

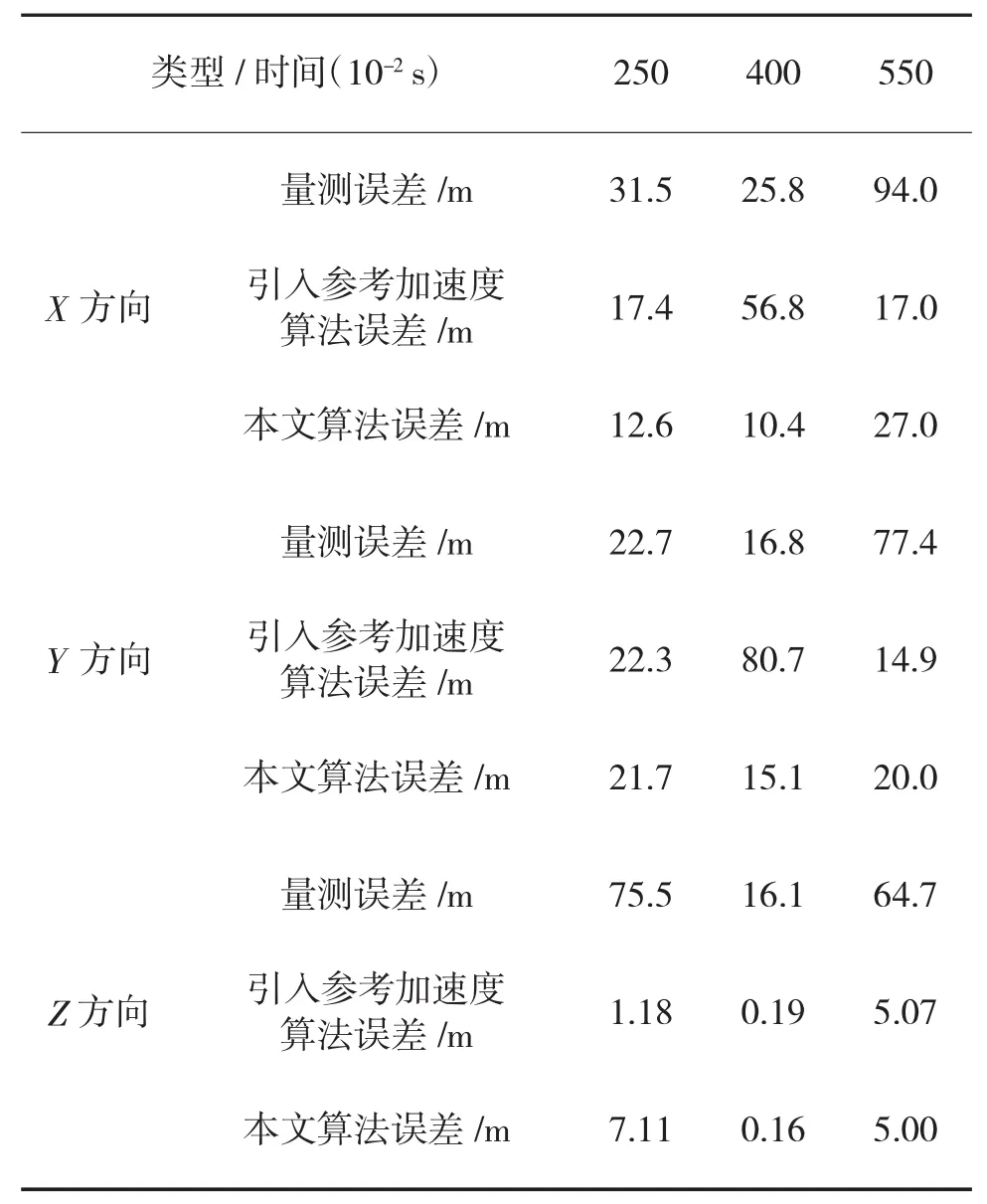
表1 误差比较

3.2 典型反舰导弹攻击航路情况

3.2.1 仿真参数设定

设目标在三维空间内进行机动，航路特征为典型高速反舰导弹攻击航路。目标前1 s作竖直面内的降高运动，降高至距水平7 m处，之后目标在水平面内作速度为2 000 m/s的匀速直线运动；当目标与舰艇水平距离15 000 m时，目标在水平面开始作比例引导运动，当距离舰艇水平距离3 000 m时，在竖直面开始作跃升俯冲运动。舰艇在高度为零的水平面作匀速直线运动。跟踪器采样频率100 Hz；跟踪时间22.6 s；观测距离和观测距变率随机误差均方差10 m；观测方位角、高低角随机误差均方差1 mrad；观测方位角、高低角变化率随机误差均方差1 mrad/s。分别取 Pμ=0.5、P0=0.2、Pmax=0.1，加速度最大值 amax=10 m/s[10-12]。

3.2.2 仿真结果

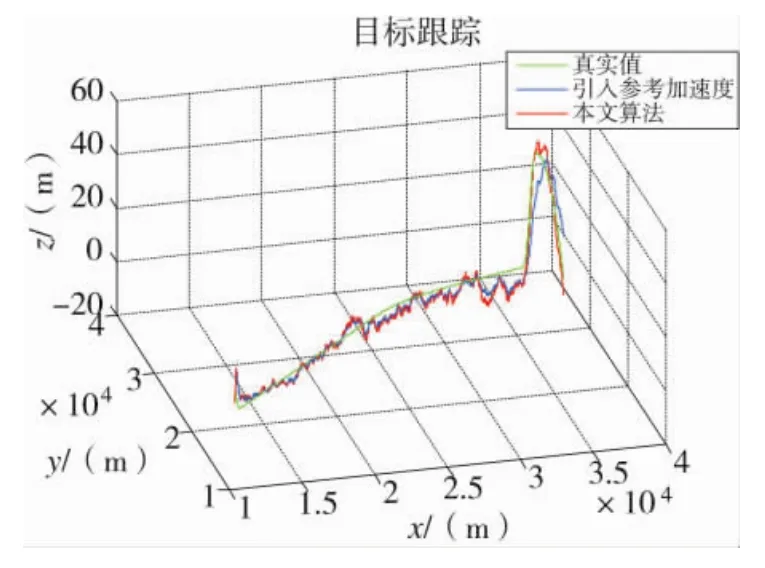
图7 目标运动轨迹及滤波效果模拟

具体各方向计算误差均方差对比如图8～图10所示。

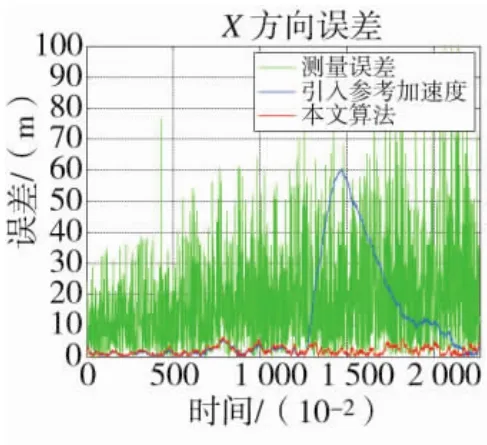
图8 X方向误差

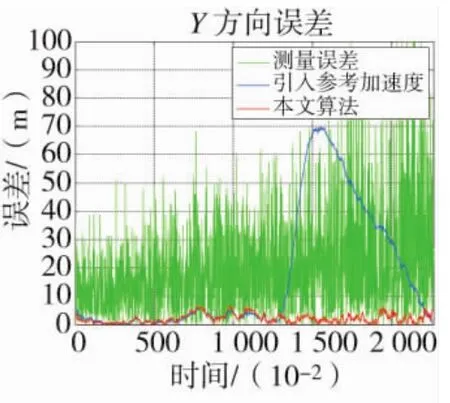
图9 Y方向误差

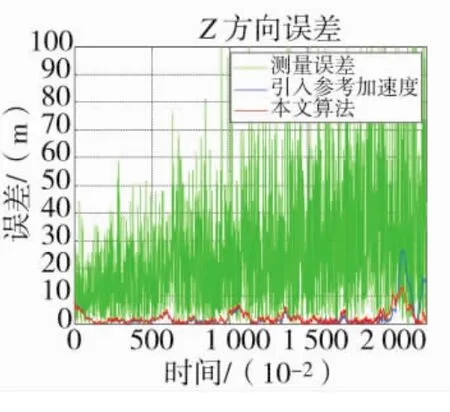
图10 Z方向误差

具体数值如表2所示。

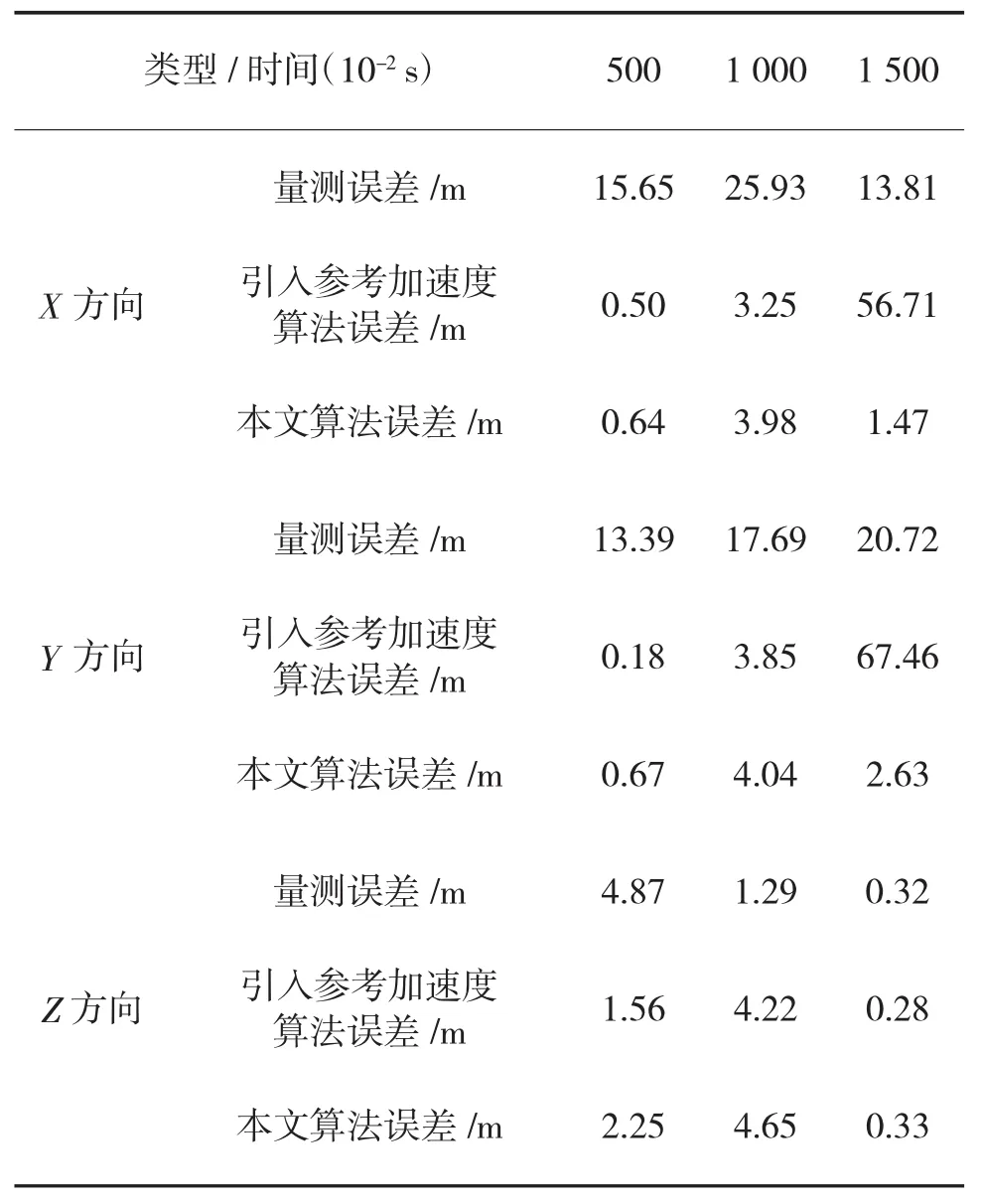
表2 误差比较

从图和表中可以看出在典型高速反舰导弹攻击航路下，改进算法在跟踪精度和机动状态改变反应速度上都有相比于引入参考加速度算法都有很大改进提高。

4 结论

文中针对高速机动目标跟踪问题，对引入参考加速度的算法进行分析，发现该算法对目标发生机动时跟踪精度低，收敛速度慢。为弥补这一缺陷，本文提出一种引入速率量测信息的三维自适应圆周运动跟踪算法，该算法对目标机动跟踪误差小，稳定速度快，并根据这一情况，建立一种新的目标运动模型切换准则，将两种算法有效结合，从而满足高速机动目标跟踪需要。经过仿真实验，验证了该算法对高速机动目标跟踪精度高、反应速度快，输出结果稳定，具有一定工程实践指导意义。