气流激励下柔性支承转子的瞬态响应

吴庭苇，王黎明，吴 雷，苏深坚

(核工业理化工程研究院，天津 300180)

高速转子一般都工作在高真空的环境中，并配备独立的抽空系统，因此高速转子具备良好的密封性能。在正常工作状态下，转子一般不会受到较大气流扰动的影响，但在特殊情况下会出现气流扰动的可能性，而且，很多外部扰动影响不会单独出现，而是多种扰动情况同时发生，例如冲击等强迫振动的出现伴随着气流扰动，这些复杂现象对转子系统的影响更为严重，甚至可能引起转子失稳等问题[1-3]。气流扰动对转子的稳定运转带来的影响非常明显，但迄今为止，气流作用下的柔性支承转子的动力学响应及稳定性问题方面缺乏系统的理论分析和试验验证[4-5]，因此有必要开展有针对性的研究。

本文针对气流作用下柔性支承转子的瞬态响应问题，建立转子模型，并在此基础上引入气流激励力，计算气流作用下柔性支承转子的瞬态响应，研究气流对转子的影响机理，并分析系统在气流作用下的运动规律。

1 气流作用下的柔性支承转子模型

分析气流进入转子的物理现象：1) 气体进入转子后，转子内充气量增大，压强升高，密封装置处内外压差升高，气体在向外逃逸的过程中形成气流激励力；2) 随着气体向外逃逸，转子内充气量逐渐减少，当充气量减少到一定水平时，气体不再逃逸，气流激励力消失。

通过对物理现象进行分析，认为气流会产生气流激励力作用于转子上。因此，建立柔性支承转子模型和气流激励力模型。

1.1 柔性支承转子模型

考虑到转子的工作状态，本文假设转子是刚体，且轴对称，不计弹性下支承质量，阻尼器仅能做平动，转子做横向微幅振动。

建立柔性支承转子模型，如图1所示。图1中，k1、k2、k3分别为上支承、下支承和阻尼装置刚度；c为阻尼装置阻尼系数；m为转子质量；mc为阻尼装置质量。

图1 柔性支承转子模型示意图Fig.1 Schematic of flexible supported rotor model

采用拉格朗日方法写出柔性支承转子系统的动能T、势能U和耗散函数D，代入拉格朗日方程，建立转子的运动微分方程：

(1)

式中：l为转子长度；ls为转子质心与转子下端距离；ω为转子角速度；Jt为赤道转动惯量；Jp为极转动惯量；r1、r2、r3分别为转子上端、下端和阻尼器的运动坐标；Q1、Q2、Q3分别为转子上端、下端和阻尼器所受的外力。

1.2 气流激励力

图2 密封装置示意图Fig.2 Schematic of sealing equipment

转子上端的密封装置与转子上壁之间存在间隙，当气流突破密封装置抽空能力上限时，气体可能从该间隙逃逸到转子和外壳的间隙中。为计算气体在逃逸过程中对柔性支承转子产生的作用力，引入Muszynska流体激励力模型[6-7]。Muszynska的研究表明，间隙中沿周向流动的流体对转子动力学特性有明显影响[8]。Muszynska在模型中假设流体具有周向平均流速τω，τ为周向平均流速比，如图2所示。该气体激励力模型将间隙中流动的气体视为参振元件，气体激励力将随该元件一起以τω旋转，对转子运动的影响具有惯性效应、阻尼效应和刚度效应，如图3所示[9-10]。

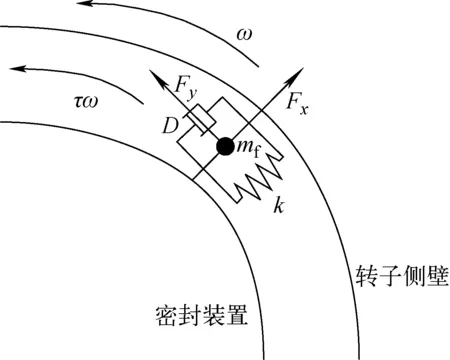
图3 气体激励下转子上端受力示意图Fig.3 Schematic of upper force for rotor under airflow excitation

在直角坐标系下，Muszynska流体激励力模型的表达式[11-13]如下：

(2)

式中：Δp为密封压降；T为流体通过密封装置时间；σ为摩擦损失梯度系数；z为进口损失系数；R为密封装置半径；λ为摩擦因子；l为密封装置长度；δ为径向密封间隙；v为流体轴向速度；ν为动力黏性系数；Rev为周向流动雷诺数；Rea为轴向流动雷诺数；n0、m0为经验系数，由实验和具体密封结构决定[14]。

本文根据密封装置的结构得到密封力所需的参数列于表1。表1中，n0、m0沿用高速旋转机械计算气流激励力的常用数值[15]，流体介质为空气，流体性质为可压缩理想气体。

表1 计算参数Table 1 Calculation parameter

2 气流激励下转子的瞬态响应计算及分析

2.1 转子的瞬态响应计算

图4 气流激励下转子上端轨迹Fig.4 Upper trace of rotor under airflow excitation

由于失效气流在管道内形成的压强远高于工作值，且进气时间较为短促，因此在计算中假设进气压强为脉冲形式。以进气压强p=1.01×105Pa、进气时间t=1 s为例，将气流激励力引入转子运动微分方程的右端，运用四阶龙格库塔方法对转子的瞬态响应进行数值计算，得到转子上端的振幅随时间变化曲线和轨迹图像，如图4～6所示。从图4、5可看出，在气流激励力的作用下，转子上端运动轨迹发生了明显变化，转子上端最大幅值增大至0.146 9 mm，约为稳定运动幅值的两倍。从图6可看出，气流激励力作用下，转子的涡动频率为14.3 Hz和605.1 Hz，该涡动频率为转子系统的一阶、二阶进动频率，该现象说明气流激励力导致转子做一阶和二阶涡动。

图5 气流激励下转子上端振幅Fig.5 Upper amplitude of rotor under airflow excitation

图6 气流激励下转子幅频曲线Fig.6 Amplitude-frequency curve of rotor under airflow excitation

根据上述结果可看出，气流在进气管道内形成的压强为1个大气压时，气流激励力会引起转子做涡动运动，对转子的动力学响应的影响很大。

2.2 进气时间对转子的影响

当气流在进气管道内形成的压强一定时，计算转子在不同进气时间下的瞬态响应。

根据转子的上端结构得知，转子上端与上校正器发生碰磨现象时会导致转子破坏，因此以转子上端与固定组件之间间隙的宽度——3 mm为转子上端的临界进动幅值，计算使转子达到临界进动幅值的进气时间，该时间即为临界进气时间。

假设外来扰动气流在进气管道内形成的压强为103、104、105、106、107Pa时，计算不同进气时间下，转子的瞬态动力学响应，结果如图7所示。

从图7a可看出，当进气管道内的压强为103Pa时，进气时间几乎对转子上端最大幅值无影响。说明当进气管道内的压强为103Pa时，进气流量较小，该强度的外来扰动气流不足以对转子的动力学响应产生影响。从图7b～e可看出，在同一强度的扰动气流作用下，进气时间越长，转子上端径向幅值越大，说明进气时间越长，气流激励力对转子瞬态响应产生的影响越大。计算得到的与进气管道内压强相对应的临界进气时间列于表2。

2.3 进气压强对转子的影响

当进气时间一定时，计算进气管道内压强对 转子瞬态响应的影响，并且计算使转子达到临界进动幅值的管道内压强，即可得到临界压强。图8为进气管道内压强与转子上端最大幅值的关系。从图8可看出，进气管道内压强为1.526 MPa时，转子的最大振幅为2.987 mm。若提高进气压强，振幅将超过固定组件与转子上端的间隙3 mm，转子上端会与上校正器发生碰撞。因此，当进气时间为1 s时，进气管道内的临界压强为1.526 MPa。

图7 进气时间与转子上端最大幅值的关系Fig.7 Relationship between intake time and upper maximum amplitude of rotor

表2 与进气管道压强相对应的临界进气时间Table 2 Critical intake timecorresponding to inlet pressure

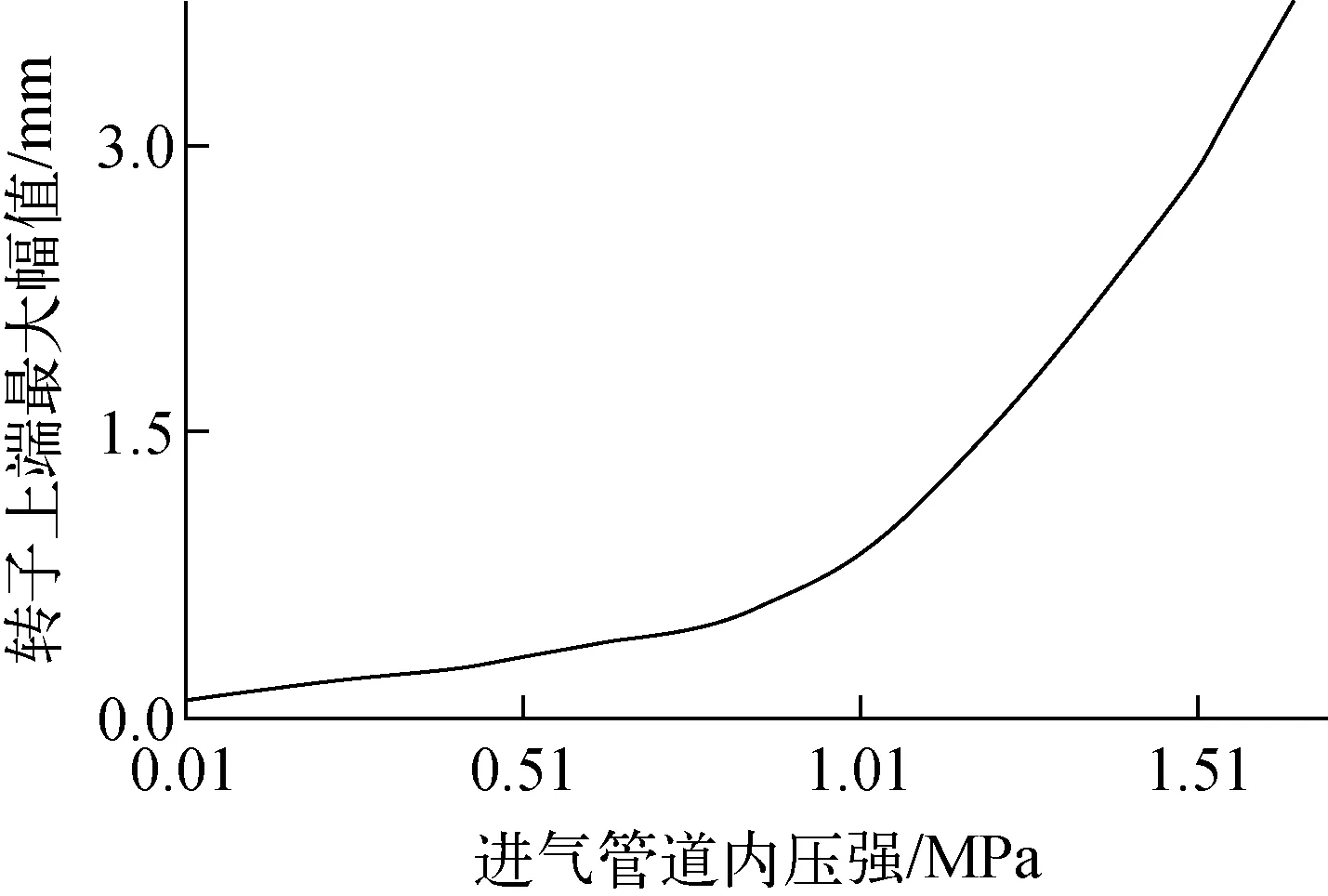
图8 进气管道内压强与转子上端最大幅值的关系Fig.8 Relationship between inlet pressure and upper maximum amplitude of rotor

3 试验验证

3.1 试验目的

在前期理论研究工作基础上，设计并开展转子受气流激励力影响试验。在进气管道放气条件下，测量转子上端涡动轨迹，研究气流激励力作用下转子的运动规律，验证理论模型的正确性。

主要测试内容列于表3。

表3 测试内容Table 3 Test content

3.2 测量结果及分析

试验中管道内的进气压强为1.01×105Pa，对转子进行进气时间不同的气流扰动试验，比较试验测得转子上端轨迹发现，进气时间越长，转子上端的最大涡动幅值越大，说明气流激励力随进气时间的延长而增大，试验现象与理论预测的趋势一致，试验中测得的转子上端涡动幅值数据列于表4。

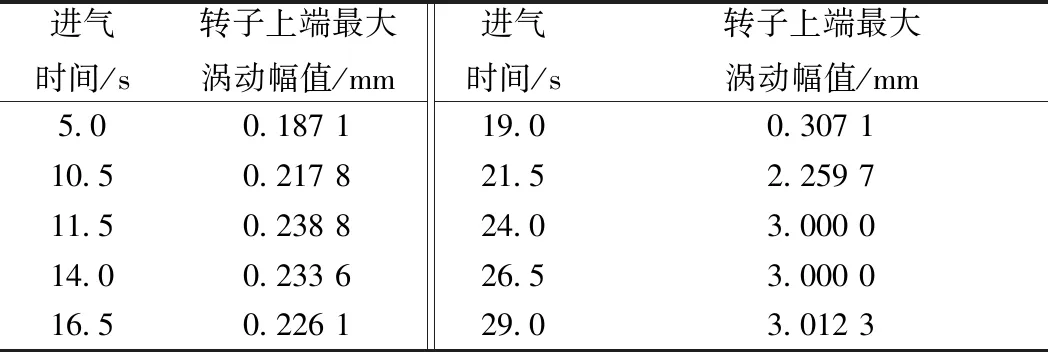
表4 不同进气时间下转子上端的最大涡动幅值Table 4 Maximum vortex upper amplitudeof rotor under different intake time

从表4可看出，当进气时间为24.0 s时，转子上端的涡动幅值达到了3 mm，此后转子上端涡动幅值不再随进气时间的延长而出现明显增长，基本稳定在3 mm左右。试验中测得的现象及转子上端涡动幅值的变化趋势说明，气流激励力随进气时间的延长而增大，当进气时间达到一定长度时会导致转子上端与固定组件相碰，影响转子的稳定运行，试验现象与2.2节中的理论计算结果的趋势一致。

图9 试验条件下转子幅频曲线Fig.9 Amplitude-frequency curve of rotorunder experiment condition

对转子的涡动运动进行幅频分析，即可得到气流激励力作用下转子的涡动频率，分析结果如图9所示。从图9可看出，转子在气流激励力的作用下做低频涡动，涡动频率为15 Hz，与转子系统的一阶进动频率相吻合。试验中的进气压强为1个大气压(1.01×105Pa)，试验现象与理论计算结果相符。

4 结论

本文通过理论分析和试验方法，对气流作用下柔性支承转子的瞬态响应进行了研究。通过引入Muszynska流体激励力模型，建立了柔性支承转子在气流激励下的计算模型；计算并分析了进气时间和进气压强对转子瞬态响应的影响规律，得到了临界进气时间和临界进气压强；设计并实施了转子受气流激励影响试验，试验中进气时间对转子动力学响应的影响规律和转子涡动现象与理论分析结果基本一致，验证了理论模型的适用性和理论分析的正确性。