级联水力学动态仿真模型研究及应用

闫 昊，李维杰

(中核新能核工业工程有限责任公司 核工程技术研究设计所，山西 太原 030012)

以往的级联研究和设计主要以静态分析为主[1-5]，缺少动态验证手段，仅靠静态分析无法解决研究和设计过程中遇到的与级联动态特性有关的问题，因此急需开展级联动态水力学研究。目前对于级联水力学的动态分析主要以小型实验级联为对象[6-10]，而工程实际级联系统在设备、结构及规模上均与实验级联存在差别，其流体特性的关注对工程实际级联系统的安全十分重要。

文献[11]建立了工程实际级联系统的动态水力学模型，针对阶梯型级联系统开发了系统仿真模型，并利用仿真系统模拟了级联的多种操作过程，仿真结果变化趋势合理，但缺少与实际数据的对比分析。文献[12]针对层架型级联系统中出现的分离单元内主机供料孔板堵塞的现象，利用模块化仿真模型搭建了动态仿真模拟系统，并开展了相应的动态测试，研究了堵塞率对分离级压强等状态参数的影响。

本文在文献[11-12]的基础上，针对层架型级联系统搭建系统动态仿真模型，结合实际运行数据对部分模块的动态仿真模型进行研究，并利用研究所得的系统仿真模型对级联动态调节过程开展相应的模拟研究。

1 级联仿真模型

1.1 分离级模型

本文所研究的基本仿真单元为分离级，每个分离级内含有若干个分离单元，由多个分离级经特定形式的组合连接可构成级联系统仿真模型，分离级仿真模型如图1所示。

根据组成分离级的各种主要部件(管道、主机、阀门、增压设备、压强调节器)的结构和工作原理分别建立各自的动力学模型[11,13-15]。

1.2 仿真模型建立

利用1.1节中各主要部件的动力学模型，根据级联系统的组成首先建立了如图1所示的分离级仿真模型，在此基础上进一步搭建了如图2所示的3层架系统仿真模型，级联分3层架运行，级联供料(f)从第1层架和第3层架供入，贫料(w)从第3层架取出，精料(p)从第1层架取出。本文的主要工作为：利用该系统仿真模型对部分动态过程进行仿真模拟，通过与实际运行数据对比分析，最终确定主机轻馏分流量方程及压强调节器动态调节方程的具体形式。

图1 分离级模型示意图Fig.1 Schematic diagram of separation stage model

图2 3层架级联示意图Fig.2 Schematic diagram of three-layer cascade

2 主机模型轻馏分流量方程的建立

对动态过程中部分分离单元的压强变化进行分析，进而确定主机轻馏分流量方程的具体形式。根据某工程实际运行数据中的动态过程，所设置的仿真模拟过程如下。

1) 第1层架K分离级第3分离单元关闭及打开过程：仿真时间为600 s，74 s时关闭分离单元供、精、贫阀门，437 s时打开分离单元供、精、贫阀门。

2) 第1层架K分离级第4分离单元关闭及打开过程：仿真时间为600 s，47 s时关闭分离单元供、精、贫阀门，306 s时打开分离单元供、精、贫阀门。

级联系统的第1层架K分离级第3分离单元内部存在异常，第4分离单元正常运行，它们可分别代表故障和正常分离单元。选择上述2组动态过程进行数据对比可检验主机模型在故障工况和正常工况下的准确性。

2.1 现有方程形式及仿真模拟结果

在以往的静态分析中给出了主机轻馏分流量方程的经验公式，其具体形式为：

Gp=G(Gf，pw)

(1)

其中：Gp为轻馏分流量；Gf为供料流量；pw为重馏分出口压强。

方程(1)是根据实验数据拟合得出的经验公式，其适用范围仅限于实验工况所覆盖的流量及压强区域。而根据所设置的动态过程，当分离单元关闭后本单元内精料端将存在不满足声速条件的情况，因此，参照孔板流量计算公式，对方程(1)进行如下改动：

Gp=G(Gf,pw)β(σ)

(2)

其中，β(σ)为与孔板后、孔板前压强比σ有关的分段函数。

将方程(2)加入系统仿真模型，进行上述2组动态过程模拟，在分离单元关闭及打开过程中本单元内的贫料压强变化如图3所示。图3中，Δp为运行压强与初始压强的差值；pR为单位压强。

从图3可看出，采用带有方程(2)形式的系统仿真模型进行模拟所得到的结果与实际运行数据相比，自分离点后压强变化速度过快，这使得分离单元内贫料压强稳定时间大幅提前，与实际情况存在差异。通过对精料孔板前、后压强进行计算分析，发现图中分离点处于孔板声速条件附近。

图4示出了2组动态过程模拟结果中分离单元精料流量的变化。从图4可看出，自分离点后精料流量下降速度明显加快，结合压强变化情况，判断当精料孔板处不满足声速条件后，采用方程(2)进行计算所得精料流量偏大，且变化速度过快。

图3 现有模型的模拟结果Fig.3 Simulation result of existing model

图4 分离单元关闭及打开过程中本单元内精料流量变化Fig.4 Change of light fraction flow in this section during dynamic process

2.2 流量方程形式确定及仿真模拟结果分析

通过上述分析可知，当主机精料端不满足声速条件后，采用现有流量方程形式计算得到的精料流量偏大，为解决上述问题，参考孔板流量计算的处理方法，对主机模型中的精料流量方程做出了如下修正：

Gp=γ(σ)G(Gf,pw)β(σ)

(3)

其中，γ(σ)=[β(σ)]a，a需根据不同的机型确定，针对本文仿真研究对象经不断试验得到a=1.5，由此得到的β(σ)和γ(σ)β(σ)的函数图像对比如图5所示。

利用带有方程(3)的系统仿真模型对上述2组动态过程再次进行模拟，所得结果如图6所示。

从图6与图3的对比可看出，采用带有方程(3)形式的系统仿真模型进行模拟，得到的计算结果与实际数据变化趋势相符，解决了当精料孔板处不满足声速条件后压强变化过快的情况。

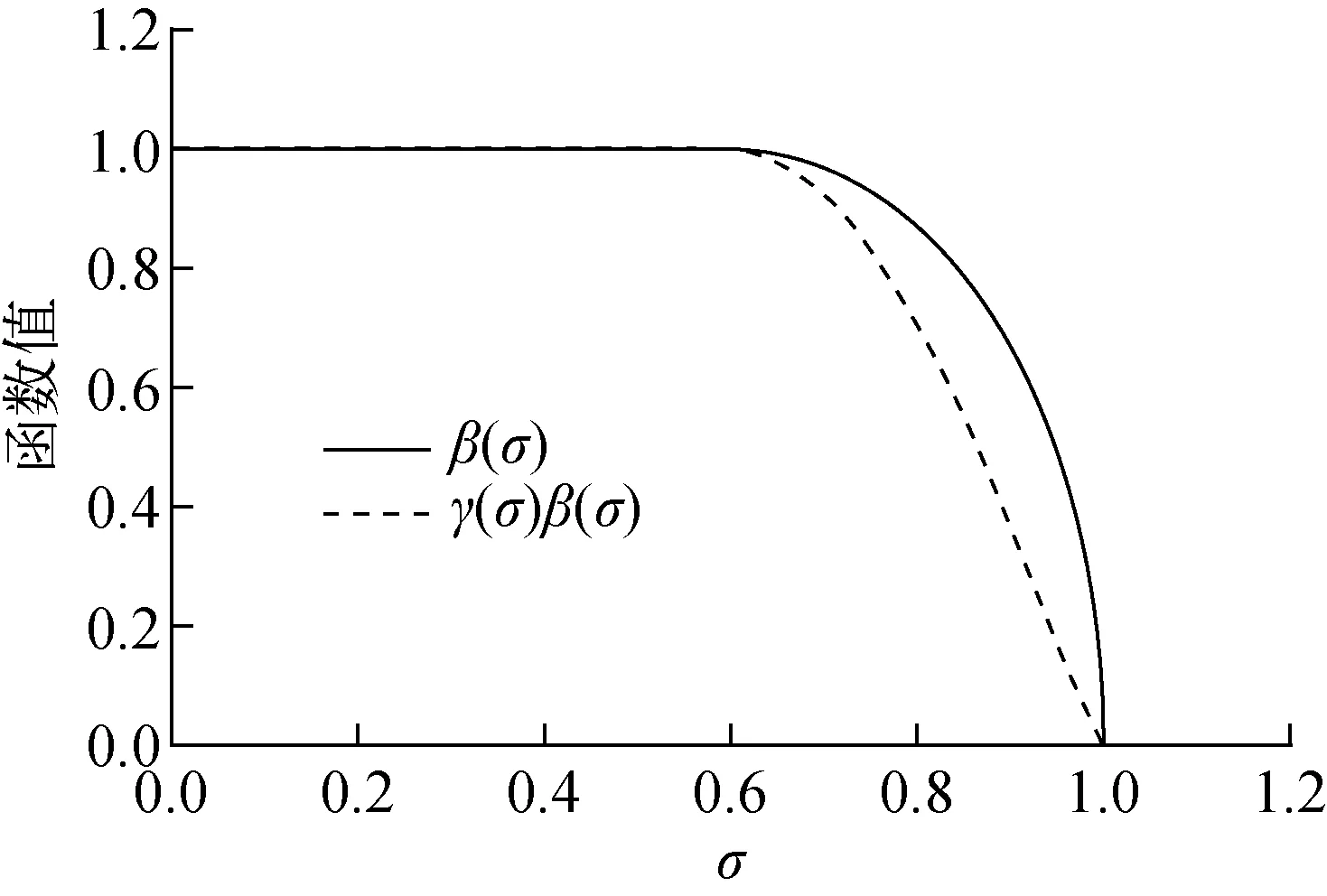
图5 β(σ)和γ(σ)β(σ)函数图像对比Fig.5 Comparison of function images for β(σ) and γ(σ)β(σ)

表1列出了采用方程(2)与方程(3)的主要仿真参数偏差对比，从表1可看出，采用带有方程(3)的系统仿真模型进行模拟，可使分离单元的压强平衡时间相对偏差小于10%，提高了仿真精度，因此可将方程(3)确定为主机轻馏分流量方程。

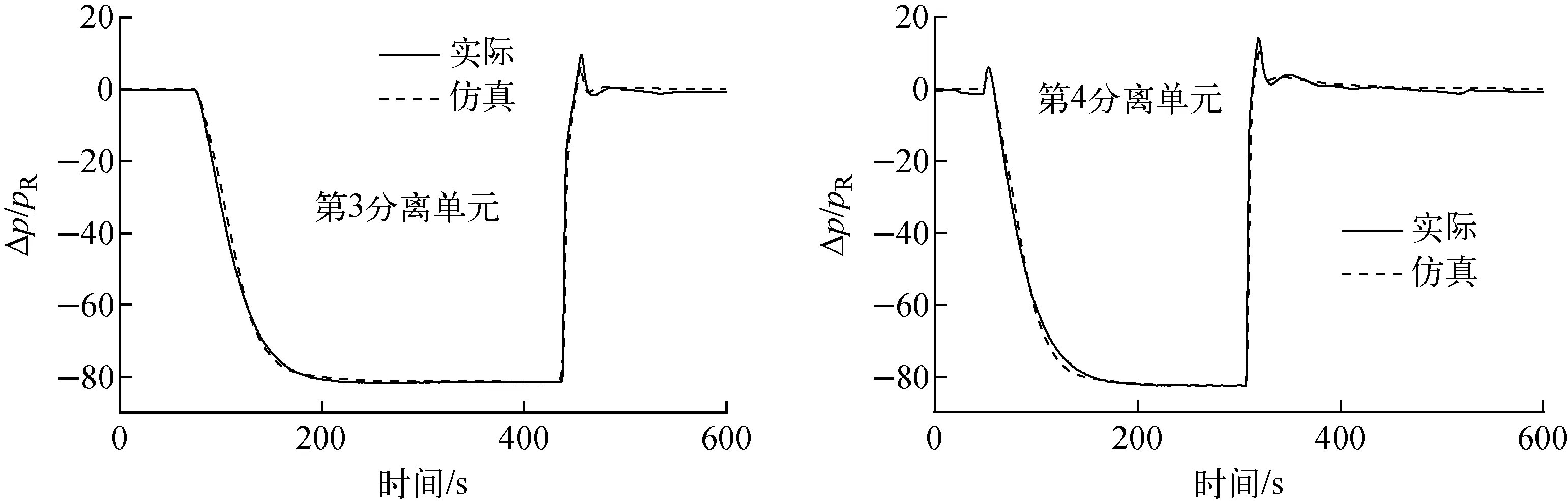
图6 改进模型的模拟结果Fig.6 Simulation result of improved model

指标仿真参数方程(2)相对偏差3)/%方程(3)相对偏差/%静态特性指标(单元关闭后)第3分离单元压强相对偏差0.0450.012第4分离单元压强相对偏差0.3240.270动态特性指标(单元关闭)第3分离单元压强平衡时间相对偏差1)28.572.29第4分离单元压强平衡时间相对偏差28.061.496第3分离单元压强最大相对偏差2)1.4891.296第4分离单元压强最大相对偏差1.9900.970动态特性指标(单元打开)第3分离单元压强最大相对偏差3.7043.649第4分离单元压强最大相对偏差5.5575.472

注：1) 距最终稳定值±10 Pa视为平衡

2) 压强最大相对偏差为动态过程中压强模拟值与实际值的最大相对偏差

3) 相对偏差=(仿真值-实际值)/实际值×100%

3 压强调节器动态调节方程的建立

压强调节器用于调节分离级重馏分管道压强，确保级联运行工况与设计工况相同，其原理是压强调节器执行机构接受反馈的压强信息，之后调整设备上的阀板行程，以达到稳定压强的目的。

压强调节器动态调节方程的一般形式为：

TRd(δH)/dt+δH=Kh(pH-pRE)pD,0/pD,0

(4)

其中：TR为调节器一阶时间常数；H为阀板行程；Kh为比例系数；pH为压强调节器工作腔压强；pRE为压强调节器执行机构参考压强；pD,0为调节器压强设定值。

方程(4)中pRE项的选取及δH项的离散格式均影响压强调节器的调节效果，本文将对分离级内的压强变化进行分析，分别确定调节器执行机构参考压强及阀板行程离散格式，进而确定压强调节器动态调节方程的具体形式。

根据工程实际运行数据中的动态过程，本文所设置的仿真模拟过程如下：第1层架K分离级第4分离单元关闭及打开，仿真时间为600 s，47 s时关闭分离单元供、精、贫阀门，306 s时打开分离单元供、精、贫阀门。

3.1 调节器执行机构参考压强的确定

在以往的静态分析中，压强调节器执行机构的参考压强pRE取本级供料干管压强pF，同样在静态分析中，对于方程(4)中的δH项通常采用阀板行程初值H0项进行离散，具体离散格式为：δH=(H-H0)/H0。

沿用静态分析方法，将pRE=pF及δH=(H-H0)/H0代入方程(4)，则可得到调节器动态调节方程为：

Hn=H(pF,H0,Hn-1,Δt)

(5)

其中：Hn为调节器阀板当前时间步的行程值；Hn-1为调节器阀板前一时间步的行程值；Δt为计算时间步长。

采用带有方程(5)的系统仿真模型进行模拟，式中H0=D/8，D为调节器阀门直径。在分离单元关闭及打开过程中部分分离级的贫料压强变化如图7所示。

图7分别选取了扰动所在分离级及该层架中贫料端某分离级的贫料压强随时间的变化，其他各分离级的贫料压强变化与这两分离级相类似，从模拟结果中各分离级的贫料压强变化情况可得到，自扰动插入点至精料端各分离级，其压强变化趋势与实际数据相一致，但自扰动插入点至贫料端各分离级，其压强变化与实际工况存在较大差异，模拟结果存在一定程度的压强振荡现象，且越向该层架贫料端，压强振荡越严重，这与实际情况不符。

经分析，这可能是由于采用静态分析方法中pRE=pF所造成的，因为在实际设备中其执行机构与本级供料干管之间还接有一段取压管及零位腔，在动态调节过程中，这两个节点能起到一定的缓冲作用。

基于上述分析，在静态分析方法的基础上增加了取压管及零位腔节点，压强调节器执行机构的参考压强pRE取本级零位腔节点压强pZ，即pRE=pZ，将该式及离散格式δH=(H-H0)/H0代入方程(4)，可得到新的压强调节器动态调节方程为：

Hn=H(pZ,H0,Hn-1,Δt)

(6)

采用带有方程(6)的系统仿真模型重新进行模拟，所得结果如图8所示。从图8可看出，

图7 参考压强为pF时的模拟结果Fig.7 Simulation result at reference pressure of pF

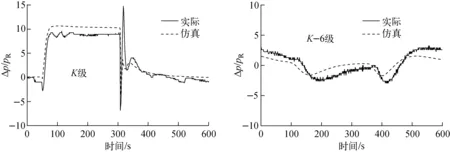
图8 参考压强为pZ时的模拟结果Fig.8 Simulation result at reference pressure of pZ

采用方程(6)可使第1层架各分离级压强变化趋势与实际工况基本保持一致，贫料压强振荡现象得以消除。由此可得出，在动态分析中压强调节器的取压管及零位腔节点不可忽略，从而确定了执行机构参考压强与零位腔压强相等，即pRE=pZ。

3.2 调节器阀板行程离散格式的确定

在静态分析方法中，压强调节器的阀板行程变化量δH的离散格式为δH=(H-H0)/H0，沿用此方法得到了方程(6)。在采用带有方程(6)的系统仿真模型进行模拟时发现，方程(6)中的阀板行程初值H0会对最终模拟结果产生影响，本文分别选取H0=D/8和H0=D/16进行模拟对比，在分离单元关闭及打开过程中部分分离级的贫料压强变化如图9所示。

图9分别选取了扰动所在分离级及该层架中精料端某分离级的贫料压强随时间的变化，其他各分离级的贫料压强变化与这两分离级相类似，从模拟结果中各分离级的贫料压强变化情况可得到，自扰动插入点至贫料端各分离级，其压强变化趋势基本一致，阀板行程初值H0对其压强变化影响较小，但自扰动插入点至精料端各分离级，当分离单元关闭后，其贫料压强变化幅度均不同程度增大，说明不同的阀板行程初值会对精料端各分离级的压强调节产生影响，压强调节器无积分调节作用，最终压强稳定值会存在残差。

实际运行时，级联各分离级压强调节过程应不受阀板行程初值的影响。为此，在动态分析中，本文选取了另外一种离散格式，目的在于消除方程(6)中的H0项，同时增加积分项。具体方式为将δH项的离散方式修改为δH=(Hn-Hn-1)/Hn-1，则可得到新的调节器动态调节方程为：

Hn=H(pZ,Hn-1,Hn-2,Δt)

(7)

其中，Hn-2为调节器阀板前两个时间步的行程值。

采用带有方程(7)的系统仿真模型重新进行模拟，所得结果如图10所示。从图10可看出，采用新的离散格式可消除调节器阀板行程初值对仿真结果的影响。

图9 不同H0对模拟结果的影响Fig.9 Effect of different H0 on simulation result

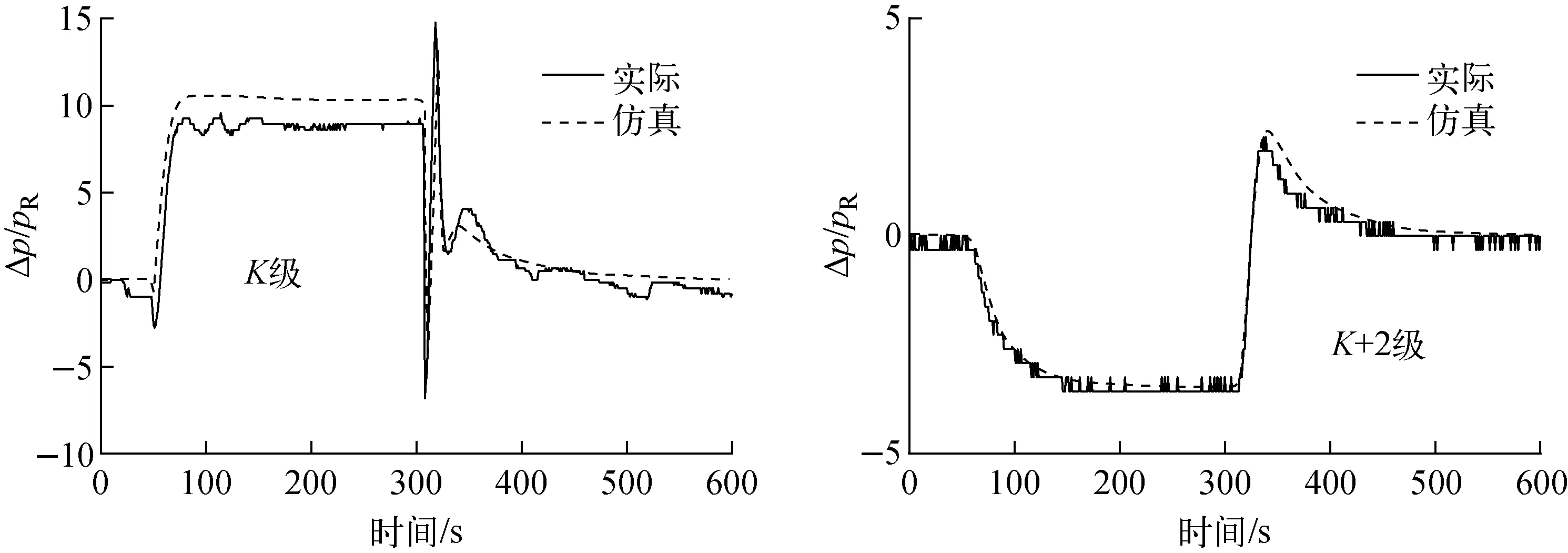
图10 改进离散格式后的模拟结果Fig.10 Simulation result of improved discrete format

表2列出了仿真模拟结果中各分离级贫料压强与实际系统参数值的相对偏差。从表2可看出，采用带有方程(7)的系统仿真模型进行模拟，可使分离级静态参数偏差小于2%，动态参数偏差小于10%，具有较高的仿真精度。由此可得出，在动态分析中阀板行程离散格式为δH=(Hn-Hn-1)/Hn-1，由此得到的方程(7)的形式可确定为压强调节器动态调节方程。

表2 仿真参数相对偏差Table 2 Relative deviation of simulation parameter

4 分离单元贫料阀门故障及仿真验证

前文确定了主机轻馏分流量方程及压强调节器动态调节方程的具体形式，由此得到了较为完善的级联系统仿真模型，并利用该系统仿真模型进行了模拟验证。通过与实际运行数据进行对比，发现采用所建立的系统仿真模型进行模拟，能较好模拟级联动态过程，所取得仿真结果与实际运行数据变化趋势相符，可利用所建立的系统仿真模型进行进一步的验证性工作。

4.1 阀门故障现象

根据实际运行数据中的动态过程，所设置的仿真模拟条件如下。

1) 第1层架K分离级第1分离单元关闭及打开过程：仿真时间为600 s，72 s时完全关闭分离单元供、精、贫阀门(所有阀门开度由1变化至0)，352 s时打开分离单元供、精、贫阀门(所有阀门开度由0变化至1)。

2) 第1层架K分离级第2分离单元关闭及打开过程：仿真时间为600 s，79 s时完全关闭分离单元供、精、贫阀门(所有阀门开度由1变化至0)，395 s时打开分离单元供、精、贫阀门(所有阀门开度由0变化至1)。

利用搭建好的级联仿真模型，进行上述2组动态过程模拟，在分离单元关闭及打开过程中本单元内的贫料压强变化如图11所示。

从图11可看出，由仿真模拟所得到的第1、2分离单元贫料压强变化与2.2节中第3、4分离单元的压强变化趋势一致，但与实际数据差别较大。在实际工况中，当分离级1、2单元阀门关闭后，本单元内贫料压强均出现先下降后上升的趋势，采用所给的仿真条件无法得到与实际工况相符的模拟结果。

根据分离单元贫料压强变化曲线，推测1、2分离单元内贫料阀门可能存在无法完全关闭 的故障情况，这样当分离单元贫料阀门关闭时会保持一定的开度，使该分离单元贫料压强逐渐下降，当低于本分离级贫料干管压强时，会有部分物料从贫料干管逆流回分离单元，当逆流流量大于由本分离单元贫料端流至精料端的流量时，会导致单元内贫料压强又逐渐上升。为验证这一推测，将通过改变仿真条件加以对比说明。

图11 现有仿真条件下的模拟结果Fig.11 Simulation result of existing simulation condition

4.2 仿真验证

根据推测，经不断试验，得到新的仿真模拟条件如下。

1) 第1层架K分离级第1分离单元关闭及打开过程：仿真时间为600 s，72 s时关闭分离单元供、精、贫阀门(供、精阀门开度由1变化至0，贫料阀门开度由1变化至0.076)，352 s时打开分离单元供、精、贫阀门(所有阀门开度变化至1)。

2) 第1层架K分离级第2分离单元关闭及打开过程：仿真时间为600 s，79 s时关闭分离单元供、精、贫阀门(供、精阀门开度由1变化至0，贫料阀门开度由1变化至0.13)，395 s时打开分离单元供、精、贫阀门(所有阀门开度变化至1)。

利用更新后的仿真条件进行模拟，所得结果如图12所示。从图12可看出，采用更新后的仿真条件进行模拟所得到的结果与实际工况趋势相符。由此可判断，在实际级联系统中，第1层架K分离级的第1、2分离单元贫料阀门存在无法完全关闭的故障情况。由于建模过程中并未得到分离单元贫料阀门的特性，本文采用平方阻力阀加以模拟，因此得到的阀门最小开度值与实际可能存在偏差，只能定性分析该阀门所存在的问题。

图12 改进仿真条件后的模拟结果Fig.12 Simulation result of improved simulation condition

从仿真模拟结果与实际工况的差异出发，假设实际系统中可能存在的问题，并通过改变仿真条件再次进行仿真模拟，所得结果与实际运行数据变化趋势一致，从而验证了分离单元贫料阀门无法完全关闭的假设。

5 结论

针对实际级联系统建立了仿真模型，并确定了主机轻馏分流量方程及压强调节器动态调节方程的具体形式，利用完善后的系统仿真模型对系统动态过程进行了模拟验证，通过与实际运行数据对比得到以下结论。

1) 静态特性指标：分离单元及分离级各测点压强仿真值与实际系统相应的参数值偏差均小于2%。

2) 动态特性指标：在相同的运行工况和操作情况下，仿真结果和实际系统的压强动态特性曲线相比，变化趋势一致，并且压强的最大偏差及系统的动态特性时间参数偏差均小于10%。

3) 建立的系统仿真模型具有较高的仿真精度，可用于其他级联系统的仿真研究。

4) 通过仿真模拟验证发现，实际级联系统第1层架K级的第1、2分离单元贫料阀门存在无法完全关闭的故障情况。