1962年～2015年堵河流域径流变化特征分析

梁小青，纪昌明，俞洪杰，阎晓冉，张验科

(1.华北电力大学可再生能源学院，北京102206；2.甘肃民族师范学院，甘肃合作747000)

1 研究背景

径流等水文循环要素在年内和年际的时空分布处于不断变化之中，存在着很大的随机性和不确定性。同时，人类活动、气候变暖等在一定程度上又加大了水资源系统的脆弱性，造成流域的径流出现诸如年内分配过度集中或年际变化十分剧烈、发生突变等情况，导致可利用水资源减少、水资源供需平衡遭受破坏、洪涝灾害频繁等情况发生[1]，严重影响了流域的水资源开发利用和经济社会的平稳健康发展。了解和掌握流域径流在一定时期内的变化特征，对于促进人水和谐发展有着很重要的意义。目前已有学者对一些流域的径流做过有关方面的研究，如海河流域、嘉陵江流域、泾河流域等[2- 4]。

堵河位于汉江上游，是汉江第一大支流，同时也承担着南水北调中线的供水任务。当前堵河流域潘口水电站、小漩水电站已陆续建成并投入使用，无论从满足流域当地的生产生活用水、生态用水，还是从提高南水北调供水率等方面来说，对堵河流域径流特性进行分析是非常必要和有意义的。目前针对堵河流域径流的研究文献较少，姚道强等[5]根据降水、流量、水位等资料对堵河流域的致洪暴雨进行了相关分析；牛利强[6]基于SWAT分布式水文模型分析了气候变化和土地利用变化对堵河径流的影响；王忠华等[7]对堵河降水、径流、泥沙等多个水文要素的时空变化及其特点进行了很好的分析与描述。本文在前人研究的基础上，采用数理统计方法[8]对堵河流域径流在年内和年际两方面的变化特征进行定性分析，以便为流域的相关工作人员提供可靠的参考依据。

2 分析方法

2.1 径流年内变化特征分析方法

采用年内分配不均匀系数和年内分配完全调节系数[9]来分析径流在年内分配的不均匀程度。前者体现了月径流之间的差异程度，后者反映了径流在年内的集中性。计算如下

(1)

(2)

运用绝对变化幅度Sa和相对变化幅度Sr来描述径流在年内的变化剧烈程度。即

Sa=Smax-Smin，Sr=Smax/Smin

(3)

式中，Smax，Smin分别为年内最大月径流量与最小月径流量。

集中度和集中期[10]两个指标分别用来表征径流在年内集中的程度及年内最大径流出现的月份。即

(4)

RCPyear=arctan(Rx/Ry)

(5)

2.2 径流年际变化特征分析方法

2.2.1 周期性分析[11]

(1)自相关系数法。对平稳随机序列Xt的一个相当长样本x1，x2，…，xn，自相关系数为

ρk=Cov(k)/σ2

(6)

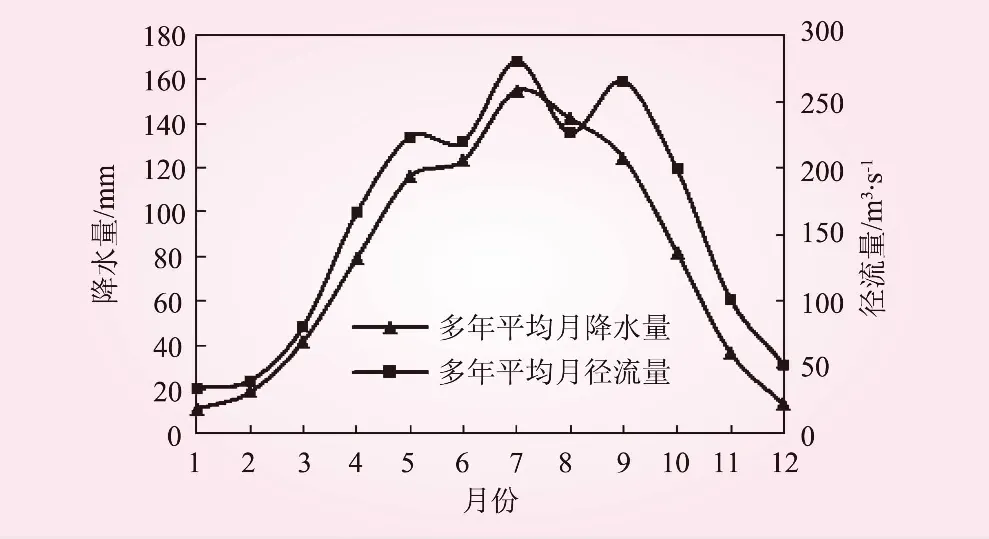
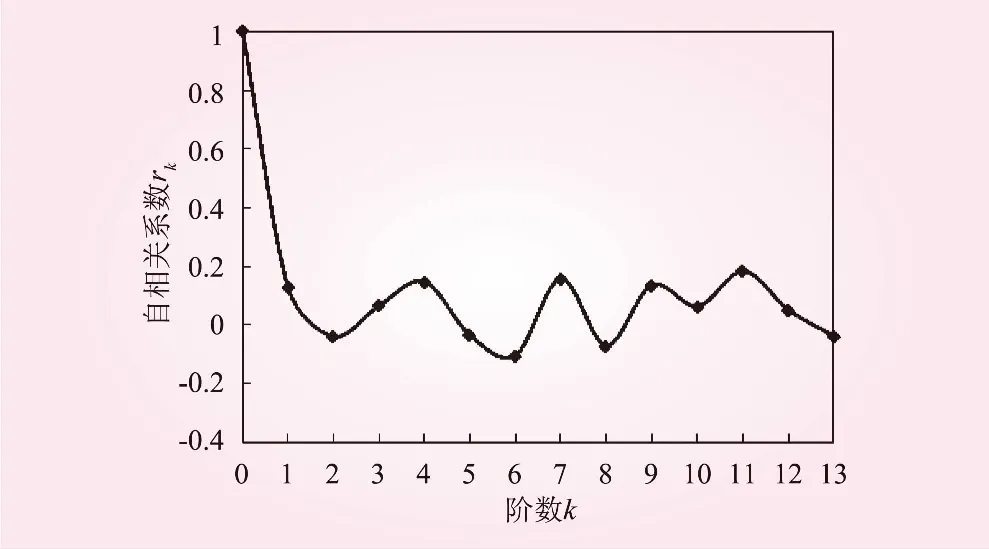
式中，k为阶数或滞时，k=0，1，…，m，当n>50时，m

(7)

(2)方差谱密度法。对离散的水文序列，有

(8)

式中，S(ω)为方差谱密度。将式(8)中ρk由样本自相关系数rk估计，∞改为最大阶数m，并加以平滑处理后，可得到无偏的样本方差谱密度

(9)

式中，Dk为窗谱，本文采用Hamming窗，Dk=0.54+0.46cos(πk/m)；fj=j/(2m)；j=0，1，…，m。绘制S(fj)-fj曲线，曲线上急剧上升的峰值处即为年平均径流序列可能的显著周期。

2.2.2 突变性分析

采用累积距平法[12]得到年平均径流序列累积距平—时间关系曲线，观察径流的丰枯变化特点，选择若干极值点对应的年份作为径流可能发生变异的年份。即

(10)

运用滑动t检验法[13]对初选突变年份前后两段径流子序列的均值进行检验，如果通过检验，则认为径流的发展趋势在所选年份处有了突变。检验统计量

(11)

2.2.3 趋势性分析

本文用Mann-Kendall非参数检验方法(以下称M-K法)[14]分析年平均径流序列在突变年前后时段的变化趋势及其显著性。设x1，x2，…，xn为年平均径流序列，M-K法定义的正态统计量

(12)

如果计算得Z>0，径流的变化表现为上升趋势；相反，如果Z<0，则径流的变化表现为下降趋势。设一定显著性水平α下的临界值为Z1-α/2，如果|Z|>Z1-α/2，则径流变化的上升或下降趋势显著；否则，不显著。

R/S法[15]是由英国学者Hurst提出的一种方法，本文利用Hurst指数(以下称H值)预测2015年后未来径流的变化趋势。H值公式如下：

(cτ)H=[maxX(t,n)-minX(t,n)]/S(τ)

(13)

式中，c为常数；τ=tn-t1为时间序列的跨度；均方差S(τ)和累积偏差X(t，n)为

(14)

(15)

当0≤H<0.5时，径流的未来变化趋势与过去的变化情况相反；当0.5≤H≤1时，径流的未来变化趋势与过去的变化情况相一致。

3 实例分析

3.1 研究区概况及数据来源

堵河流域地处鄂西北地区，位于北纬31°21′～32°50′，东经109°30′～110°40′之间，是汉江中上游南岸一大支流，发源于大巴山北麓，有西、南两源。西源名泗河，为堵河主流，发源于陕西省镇坪县境内，河道长270 km，平均坡降0.200%，流域面积4 848 km2；南源为官渡河，发源于川鄂交界的阴条岭及乌云顶，河长约126.9 km，平均坡降0.473%，流域面积2 961.1 km2。两源在两河口汇合后始称堵河，向下经田家坝镇、潘口坝址、竹山县城进入黄龙滩水库，由西南流向东北汇入汉江。堵河属于山区型河流，河谷深窄，滩多流急，全长354 km，流域面积12 502 km2。本文研究所用数据为1962年～2015年潘口上游流域逐月平均降水量和竹山水文站逐月平均径流量。

3.2 年内变化特征

根据1962年～2015年堵河逐月降水量和逐月径流量数据得到多年平均月降水量与多年平均月径流量，其在年内的分配情况见图1。从图1可以看出，降水在年内的分配呈单峰型，峰值在7月份；径流在年内的分配呈多峰型，峰值在5月份、7月份和9月份。这些说明降水在经过下渗、蒸发、产汇流等过程后使得径流在年内的集中程度较降水偏小，年内分配趋于均匀。径流与降水的年内丰枯变化规律基本一致，说明径流受降水的影响程度很大。多年平均月径流量中，7月份达到最大值280 m3/s，其径流量占年径流总量的16.05%；4月～10月份之间水量丰沛，径流量约占年径流总量的83.67%；1月份最枯，径流量约占年径流总量的1.86%。

图1 1962年～2015年堵河流域多年平均月降水量与多年平均月径流量

径流的年内分配不均匀系数Cv和年内分配完全调节系数Cr、绝对变化幅度Sa和相对变化幅度Sr变化情况如图2和图3所示。

图2 年内分配不均匀系数Cv和年内分配完全调节系数Cr

图3 绝对变化幅度Sa和相对变化幅度Sr

由分析可知，径流年内分配不均匀系数在0.45～1.18之间，年内分配完全调节系数在0.2～0.44之间，前者的变幅稍大于后者。从图2可以看出，年内分配不均匀系数和年内分配完全调节系数的变化基本一致，在20世纪70年代、80年代以及21世纪后，径流年内分配不均匀程度显著，表明月径流之间的差异较大，年内集中程度较高，其余时段径流年内分配比较均匀。从趋势线变化来看，径流的年内分配不均匀系数随年份的增加呈微弱的增加趋势，年内分配完全调节系数随年份的增加呈微弱的下降趋势，说明月径流之间的差异越来越大，在年内的集中程度有所降低。图3趋势线显示，径流量的绝对变化幅度和相对变化幅度均呈减小趋势，说明径流的年内变化幅度正逐渐向平缓的方向发展。

径流量集中度与集中期的计算结果如表1所示。从集中度来看，各个时期的集中度在多年平均值40.12%上下波动，在20世纪80年代达到一个峰值后有所下降，在2010年后又处于一个峰值阶段，并且较20世纪80年代的集中程度更大；从集中期来看，径流在各年代均集中在7月份，集中时段比较稳定。

表1 径流量集中度RCDyear与集中期RCPyear

3.3 年际变化特征

根据月径流量资料得到年平均径流量，其变化情况如图4。从图中可看出，径流在1962年～2015年的54 a间进行着丰枯交替的变化，1983年达到最大值266.7 m3/s，2012年为最小值72.2 m3/s，多年平均值为157.3 m3/s。随着年份的增加，堵河径流呈逐渐减少的趋势。

图4 年平均径流量变化情况

3.3.1 周期性分析

首先对年平均径流序列在时域上进行周期性分析。本文所研究径流序列资料的年份数n为54 a，则m=n/4=13.5，由于n>50，所以取m为13。径流的样本自相关图见图5。从图5中可以看出，阶数k为4、7、11时，对应点的自相关系数大于邻近点的自相关系数，故初步推断径流的波动周期为3～4 a。

图5 径流样本自相关系数

为了进一步了解径流序列的周期性，采用谱分析方法从频率域上进行分析。年平均径流序列的方差谱密度变化过程见图6。由图6可知，年平均径流序列有3.7 a和2.4 a左右的周期。

图6 径流样本方差谱密度

3.3.2 突变性分析

根据1962年～2015年月径流量资料，得到年平均径流累积距平曲线(见图7)。

图7 径流累积距平曲线

由图7可知，1985年～1993年之间曲线位置最高，没有明显的上升或下降趋势。初步选取三个极值点1985年、1989年、1993年作为可能突变点，位于曲线两端的年份不是极值点，不作为可能突变点来进行研究。

运用滑动t检验法对突变点进行检验，在突变点前后均取以5 a为滑动步长的两个径流子序列，显著性水平α取0.1，检验结果如表2所示。

表2 年平均径流序列滑动t检验法检验结果

由表2可知，只有1985年附近径流序列的统计量绝对值大于临界值，通过检验，所以1985年为突变年。

3.3.3 趋势性分析

由于年平均径流序列在1985年发生了突变，因此以1985年为界将径流序列划分为1962年～1985年、1986年～2015年2个时段。对每一时段的径流序列，分别用M-K法进行趋势性分析及显著性检验，显著性水平α取0.05，检验结果如表3所示。

表3 年平均径流序列M-K法检验结果

表3显示：1962年～1985年的统计量值为正值，表明这段时期该流域年径流量出现上升趋势；但其绝对值小于临界值1.96，说明上升趋势不显著。即，1962年～1985年间，年径流量呈微弱的上升趋势。而1986年～2015年的统计量值为负值，表明这段时期该流域年径流量出现下降趋势；但其绝对值小于临界值1.96，说明下降趋势也不显著。即，1986年～2015年间，年径流量呈微弱的下降趋势。总体来看，1962年～2015年间，流域径流量呈现先上升后下降的趋势，两种变化趋势均不显著。

采用R/S法分析2015年以后未来年份的径流变化趋势，结果如表4所示。由表4可知，1962年～1985年径流序列的H值为0.489，小于临界值0.5，说明1985年后的若干年份内径流序列会与过去年份的变化趋势相反，即由上升变为下降趋势；1986年～2015年径流序列的H值为0.437，小于临界值0.5，说明2015年后未来若干年份内径流序列也与过去年份的变化趋势相反，即由下降变为上升趋势。2015年的径流量值为123.7 m3/s，根据竹山水文站提供的2016年和2017年径流量值分别为125 m3/s和221.8 m3/s，验证了预测结果的可靠性。

表4 年平均径流序列R/S法趋势分析结果

3.4 径流影响因素分析

堵河流域年径流量由降水补给，但在径流趋势发生突变的1985年前后两个时段(1962年～1985年和1986年～2015年)，径流与降水的相关系数由0.943变为0.773，相关性由强到弱。因此，可认为在1986年～2015年期间，除了降水以外，下垫面条件也对径流产生了影响。忽略1985年以前下垫面对该流域径流的影响，根据1962年～1985年降水、径流资料建立回归方程

y=0.328 3x-150.32

(16)

式中，y为年平均径流量，m3/s；x为年降水量，mm。

将1986年～2015年期间的年降水量值代入式(16)，可得到1986年～2015年间不受下垫面影响下的年平均径流量值，将其与该时间段的实际年平均径流量值相比较可知，1985年后下垫面条件的变化使径流的多年平均值减少了5.81 m3/s。计算1962年～1985年、1986年～2015年两时段多年平均径流量之差[16]可得出在降水和下垫面的共同影响下，多年平均径流量减少了37 m3/s。由上述分析可知，突变年后降水对径流减少的贡献率大于下垫面。堵河流域1985年后下垫面条件的变化主要是人类活动的影响所致。如，南水北调供水、梯级水电开发等。

4 结 语

本文应用数理统计理论采用多个指标、多种方法对堵河流域径流的年内、年际变化特征进行了研究。从年内变化看，随着年份的增加，径流的年内分配正缓慢地向着不均匀的方向发展，年内变化幅度有所减弱。虽然各个时期径流的集中期均稳定在7月份，但其集中程度在目前仍然处于一个比较高的状态。从年际变化看，径流序列有2个较短的周期，在1985年出现突变，突变年份前后的上升和下降趋势均不显著；2015年以后一段时期内，流域的径流将会有增加的趋势。影响径流的主要因素是降水，下垫面次之。准确地定量分析不同因素对堵河径流特性影响的贡献率及综合影响需要更进一步的研究。