基于粗糙表面分形表征新方法的结合面法向接触刚度模型
2019-04-22孙见君张凌峰於秋萍嵇正波马晨波
孙见君, 张凌峰, 於秋萍, 嵇正波, 马晨波
(南京林业大学 机械电子工程学院,南京 210037)
机械结构中结合面的接触刚度对结构的动态性能影响巨大。有研究[1]表明,机床结合面的刚度约占机床总刚度的60%~80%,结合面引起的变形量约占机床总的静变形量的85%~90%。机床结构设计时,如何有效预测结合面的动态参数,如结合面接触刚度,是机床动力学建模的一个重要问题。目前的结合面接触刚度计算模型主要有基于统计学参数和分形参数的两种。基于统计学特征参数研究获得的结合面接触刚度计算模型[2-7],因为采用了粗糙表面的统计数据,其准确度受制于仪器的分辨率。20世纪90年代初,Majumdar等[8]提出的采用分形参数D,G和微凸体接触面积表征等效粗糙表面特性的方法,为研究者[9-11]进一步研究结合面接触刚度模型提供了新的途径。温淑花等[12-13]对M-B表征方法进行了修正,考虑弹塑性过渡变形机制,建立了法向接触刚度弹塑性分形模型;杨红平等[14]研究了微凸体由弹性变形向弹塑性变形和完全塑性变形转化时,不同的塑性指数下接触载荷与法向刚度的关系。Jiang等[15]在M-B分形接触模型基础上推导了粗糙平面的法向接触刚度,并进行了试验验证。Buczkowski等[16]基于分形理论,考虑微凸体在受载过程中的相互强化作用,建立了粗糙表面法向刚度模型。然而,基于M-B的轮廓表征方法,人们获得的“微凸体先发生完全塑性变形,再发生弹塑性变形、弹性变形”的结论[17-19]有违常理,建立的剔除了“微凸体完全塑性变形”加载初始阶段的法向接触刚度表达式因实验时无法将加载初始阶段的塑性变形值从总变形量中分离出来而使所做的验证缺乏效力。Morag等[20-21]注意到这一问题,并采用微凸体基底开口尺寸描述微凸体轮廓,纠正了M-B模型中微凸体变形是从塑性变形起向弹性变形模式转变的错误;但是,Chen等[22]将取样长度L=1/γn作为最大微凸体基底尺寸,以及据此推导出的与取样长度相关的结合面接触刚度模型值得商榷。可见,结合面法向接触刚度模型仍有待于更为深入的探讨。
本文拟基于确定粗糙表面的初始轮廓与接触面积无关的思想,采用D,G和与最大微凸体高度表征分形粗糙表面轮廓,探讨微凸体的变形状态判据和微凸体接触变形机制,建立粗糙表面的接触刚度分形模型,并将模型计算结果与文献实验数据比较,考察模型的正确性,据此分析接触刚度变化规律,以期为新建模型的应用提供理论基础。
1 粗糙表面轮廓分形表征新方法
1.1 分形粗糙表面的接触表征
两个各向同性的粗糙表面的接触可以等效为一个粗糙表面与一个刚性光滑平面的接触,其粗糙表面二维轮廓曲线可采用Weierstrass-Mandelbrot函数(W-M函数)表征[23]
(1)
式中:Z(X) 表示粗糙表面轮廓曲线的高度;X为轮廓的位置坐标;D为表面轮廓分形维数;G为轮廓特征尺度系数;γn表示轮廓曲线的空间频率,nmin为最低层次指数;γ为大于1的常数,对于服从正态分布的表面,取γ= 1.5。轮廓曲线由D,G和nmin3个参数决定,D和G可由二维W-M函数的功率谱获得,最低层次指数与最大微凸体的高度有关。图1为一等效粗糙表面与一个刚性光滑平面的接触。其中L,H分别为最大微凸体轮廓底面直径和高,L′、H′分别为第二大微凸体轮廓底面直径和高;Δ为一定载荷下最大微凸体法向变形量;L是在以最大的波谷处为基面得到的最大微凸体底面直径。
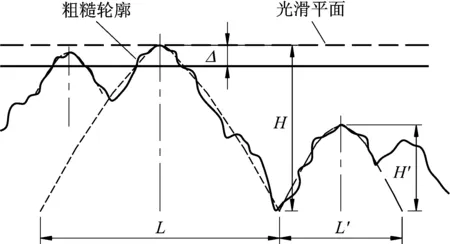
图1 一等效粗糙表面与一个刚性光滑平面的接触Fig.1 Contact between a rough surface and a rigid flat plane
1.2 粗糙表面微凸体轮廓分形表征
对于公式(1)描述的由一系列不同尺寸的余弦波状微凸体叠加而成的粗糙表面,如果忽略接触过程中微凸体之间的相互作用、微凸体发生变形时的宏观基体变形、接触过程中材料硬化以及微凸体间的摩擦,并假设微凸体在垂直于粗糙度深度方向的任一截面均为圆截面,则粗糙表面上的任何一个微凸体,变形前的轮廓曲线均可描述为
(2)
式中:l为微凸体轮廓底面直径,l=1/γn。当n=nmin,最大微凸体的基底l=1/γnmin=L;当n=nmin+1,对应微凸体的基底l′=1/γnmin+1=L′;以此类推,可获得各对应微凸体的基底尺寸。
考虑到微凸体原始轮廓的表征参数不因承载而变化,这里定义的l与Majumder等[8]描述的与载荷作用后形成的微凸体接触面对应的轮廓开口尺寸不同,而是一个只与微凸体高度相关的参数。
图2为单个接触微凸体及其接触变形示意图,h为微凸体的高度幅值。

图2 单个微凸体的接触变形Fig.2 Contact deformation of a single asperity
根据式(2),微凸体高度可以表示为
h=GD-1l2-D
(3)

通过式(3),可以计算出l。由此获得的式(2),只与D,G和Ls相关,而与测量尺度无关。
粗糙表面微凸体峰点处的曲率半径为
(4)
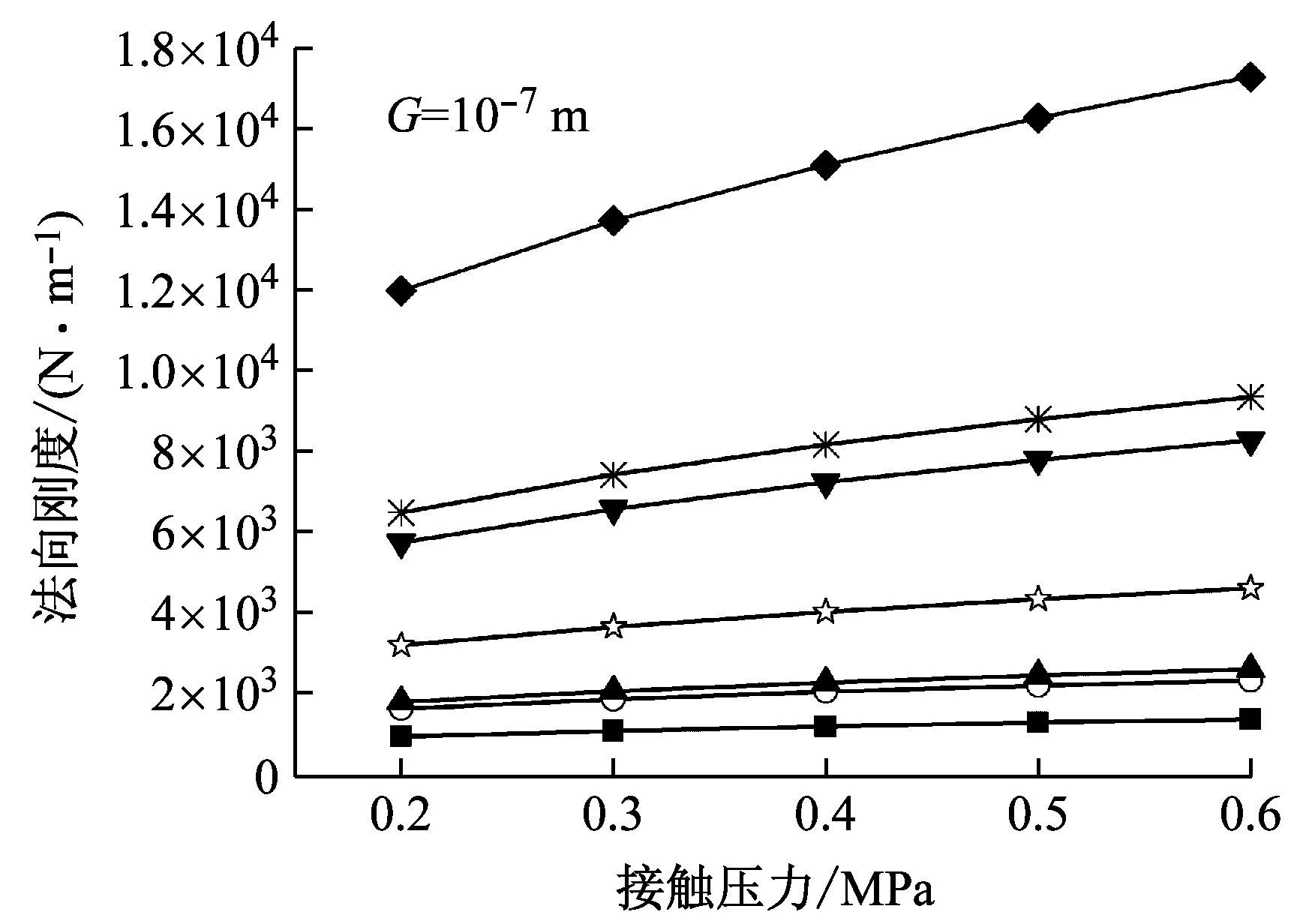
图2中δ为实际压缩量,取值范围为 0≤δ 通过简化 (a)1/2=(πr2)1/2=2x (5) 考虑到变形前后微凸体体积相等,并比较简化成圆台后的微凸体体积与变形前的体积,求取V1-V0极值,可获得简化公式(5)给变形带来的误差为(V1-V0)/V0=3.24%。 利用图2所示的几何关系,实际压缩量δ可表示为 (6) 实际压缩量δ是由变形情况,即接触点产生弹性变形、弹塑性变形或塑性变形情况决定的。 在接触压力作用下,粗糙表面上的微凸体存在3种可能的变形状态,即弹性变形、弹塑性变形和完全塑性变形状态。 (1)弹性变形状态:按照Hertz接触理论,一定接触压力下微凸体的接触面半径r可表示为[25] (7) 当接触面上的平均接触压力pm小于粗糙表面材料的屈服极限σy时,微凸体处于弹性状态;弹性接触压力pe可用pm表示,即 (8) 当pm=σy时微凸体出现初始屈服。将式(4)、(8)代入式(7),则临界弹性变形面积aec可以表示为 (9) 如果微凸体接触面积a≤aec,则发生弹性变形;否则,微凸体将发生弹塑性或完全塑性变形。 (2)完全塑性变形:当接触面上的平均接触压力pm=3σy时,微凸体完全屈服[26],即塑性接触压力pp=3σy,此时 (10) 将式(4)、(7)代入式(10)可得 (11) 如果微凸体接触面积a>apc,则微凸体发生完全塑性变形。 (3)弹塑性变形状态:当aec≤a≤apc时,微凸体处于弹塑性变形状态,这一阶段微凸体接触面积和接触压力的关系极为复杂。考虑到在初始屈服临界点和完全塑性变形临界点,接触压力的变化是连续和光滑的,利用文献[27]构造样板函数 (12) 可导出弹塑性变形时的接触压力 pep=pe+(pp-pe)f(a) (13) 分形粗糙表面接触载荷Fc与最大微凸体的变形状态相关。接触面上的接触面积大小分布密度函数n(a)可表示为[28] (14) 式中:a为微接触点的面积;Ψ为真实接触面积与最大微接触点面积之比Ar/aL的修正系数;aL为微接触点的最大面积。 对于aL (15) 对于aec≤aL (16) 对于aL≥apc,接触表面上的接触点处于塑性变形、弹塑性变形和弹性变形状态,所承受的载荷Fc为弹性载荷、弹塑性载荷与塑性接触载荷三者之和,即 (17) 由式(15)~(17)和式(3)可知 Fc=F(E,D,G,h,aL) (18) 结合面的法向接触刚度等于接触压力对法向压缩量的一阶导数。考虑到粗糙表面的压缩量与最大微凸体的变形量一致,则由式(18)与式(6)联立,可得粗糙表面的法向接触刚度 (19) 式中:aL可依据式(18)求得。之所以这样描述法向接触刚度,是因为粗糙表面的法向接触刚度不同于微凸体接触刚度,即在接触压力的作用下,即使aL>apc,接触表面上仍有弹性变形状态的接触点存在,并随着接触界面间空隙被压实,甚至成为近似刚体。 当aL (19a) 本文模型计算刚度与Jiang等[15]实验数据的比较如图3所示。材料为铸铁,等效粗糙表面的弹性模量E=100 GPa,粗糙度Ra=1.44 μm,采用结构函数法计算获得的分形参数D=1.405 8,G=2.282 6×10-10。本文模型计算刚度与实验值具有相同的变化趋势,在接触荷载小于1.2 MPa时,两者吻合度高,当接触载荷大于1.2 MPa后,误差趋大。本文刚度模型计算值偏离实验值的主要原因在于:①采用结构函数法计算的分形维数D比实际的大[29],尤其是小于D<1.5时更是如此,这就意味着实际粗糙峰比模型粗糙峰尖削,在接触压力作用下,其变形量较理论粗糙峰的大,从而导致初始接触时实测刚度小于理论模型计算刚度值。②本模型忽略了接触变形过程中相邻接触微凸体之间的相互作用,以及形变时材料强化作用;实际上,接触压力越大,相邻接触微凸体之间的相互作用即材料流动的阻力将越大,表现为实验刚度值也就越大。 图3 本模型刚度与Jiang的实验数据比较Fig.3 Comparison with the Jiang’s test data 图4和图5分别描述了分形参数D,G和接触压力对法向接触刚度的影响。随着分形维数或接触压力的增大,法向接触刚度增大;随着尺度系数的增大,法向接触刚度减小。这是因为:分形维数的增大,使得微凸体基底尺寸增大,微凸体轮廓变得更加扁平,微凸体法向变形时承载面积增大速度快,承载能力急速增大;接触压力的增大,使得接触面下移,接触面积增大,承载能力急速增大;尺度系数的增大,微凸体波峰值增大,获得相同承载面积时接触压力作用引起的法向变形较大。当G≤10-10m,D=1.6或D≥1.6,G=10-10m时,粗糙表面的空隙已经压实,变为刚体。 (1)提出了一种基于D,G与最大微凸体高度相关的粗糙表面轮廓分形表征方法。这种方法的应用,保证了确定粗糙表面的原始轮廓特征参数不因承载力大小的变化而变化。 (2)结合面的接触载荷可以采用表达式Fc=F(E,D,G,h,aL)描述。 (3)当结合面上的接触压力小于其屈服强度时,不论微凸体发生弹性变形、弹塑性变形还是塑性变形,结合面均因存在有弹性变形的接触点而具有一定的法向接触刚度。当aL (4)分形参数D,G和接触压力对法向接触刚度的影响显著。随着分形维数或接触压力的增大,结合面的法向接触刚度增大;随着尺度系数的增大,结合面的法向接触刚度减小。对于由分形粗糙表面与刚性平面构成的结合面,存在某一接触压力,在这一接触压力下,其空隙被压实,结合面将成为近似刚体。
2 粗糙表面真实接触面积接触载荷分析
2.1 微凸体接触变形机制

2.2 粗糙表面接触载荷
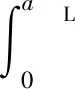
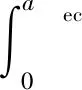


3 结合面的法向接触刚度模型
4 与实验数据的比较
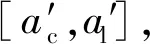

5 接触刚度变化规律讨论
6 结 论