柔性机械臂残余振动控制

杜严锋， 王 聪

(哈尔滨工业大学 航天学院，哈尔滨 150001)

近年来随着航天技术的不断发展，为了提高运载工具的效率，增大有效载荷，航天器的附件结构逐渐呈现轻质、柔性等特点，如太阳翼、卫星天线和空间机械臂等结构。这类柔性结构在执行运动任务过程中很容易产生较大的残余振动，影响操作精度，甚至会影响结构的安全。为了使这类结构快速精确地完成机动任务，很多研究人员从不同方面进行了广泛的研究。为了对柔性结构运动后的残余振动进行控制，主要的方法为被动控制和主动控制等。其中被动控制主要通过在柔性结构上附加阻尼结构，来增加柔性结构的阻尼，吸收结构振动的能量，或者附加隔振结构隔离振动的能量，使残余振动很快衰减。主动控制主要包括前馈控制方法和闭环反馈控制方法等，前馈控制是指通过调节输入指令使柔性结构完成机动任务的同时减小残余振动，闭环反馈控制是指将柔性结构的振动用传感器测出，经过信号传递将振动信号反馈给控制系统，控制系统输出指令使作动器控制结构的振动。被动控制方法对结构的高频振动具有较好的抑制效果，但是对结构的低频振动不能起到很好的抑制，主动控制方法由于在设计方面非常灵活，从而引起了研究人员的极大兴趣。

前馈控制方法主要包括分力合成方法、输入整形方法和S曲线方法等。Shan等[1]介绍了分力合成方法(Component Synthesis active Vibration Suppression,CSVS)抑制振动的原理，并将分力合成方法应用在柔性机械臂的残余振动抑制方面，结果显示分力合成方法使机械臂在完成机动动作的同时很好地抑制了残余振动，Shan等还分析了分力合成方法对系统建模误差的鲁棒性。在CSVS方法的基础上，Zhang等[2]基于零点配置方法设计了合成力来同时消除多模态残余振动。Singhose等[3-4]采用了输入整形方法来抑制残余振动并分析该方法的鲁棒性。除了CSVS方法和输入整形方法以外，采用S曲线运动方式[5-7]来抑制残余振动的方法也被广泛研究。

在闭环反馈控制方法中，往往需要在结构上附加压电传感器和压电作动器，压电传感器测量并向控制系统传输柔性结构的振动信号，压电作动器接受控制系统的指令控制柔性结构的振动。董兴建等[8]在悬臂梁上附加压电材料作为传感器和作动器，并对压电悬臂梁进行了动力学建模，采用极点配置方法实现了对悬臂梁的振动主动控制。曹青松等[9-10]考虑了刚柔电相互耦合，利用模糊自整定PID算法，对压电机械臂的振动控制进行了研究。姜晶等[11]将镧改性锆钛酸铅用作压电作动器，利用光电效应实现了对结构振动的光学控制，并采用独立模态控制方法对悬臂梁的振动控制进行了研究。陈希等[12]考虑压电片不同粘贴位置，对柔性臂的振动控制进行了实验研究，并得到了压电片的最优控制位置。闭环反馈控制方法还包括正位置反馈控制方法[13]、变结构控制方法[14]和模态预测控制方法[15]等。其中正位置反馈控制方法采用柔性结构的广义位移作为反馈来抑制柔性振动，广义位移可以由传感器测出柔性结构的应变经过变换得到，这就使得正位置反馈方法实现起来比较简单和直接，并且正位置方法可以有效地增加柔性结构的模态阻尼。变结构控制方法具有很强的鲁棒性，可以有效地处理柔性结构系统参数不确定和存在干扰力的情况。模态预测控制方法在系统存在多变量和高度非线性时具有很好的控制效果和鲁棒性。但是由于闭环反馈控制通常需要为柔性结构附加传感器和作动器结构，相对前馈控制来说较为复杂，所以本文通过调节柔性结构的输入指令来控制柔性结构的残余振动。

本文主要研究了柔性机械臂的残余振动控制问题，用一次近似刚柔耦合模型对柔性机械臂进行了建模，得到了非惯性系下柔性机械臂的刚柔耦合模型。并用所建立的动力学模型对柔性臂系统进行了数值仿真，研究了柔性机械臂的残余振动与机械臂的运动规律和运动参数的关系。

1 柔性机械臂动力学模型

1.1 柔性机械臂模型介绍

如图1所示为柔性机械臂结构模型，柔性机械臂结构主要由中心刚体、柔性杆和末端质量组成。柔性杆的一端固定在中心刚体上，另一端连接末端质量。图1中O0X0Y0为惯性坐标系，ObXbYb为浮动坐标系，未变形的柔性杆与末端质量用虚线表示，柔性杆变形后的柔性杆与末端质量用实线表示。其中浮动坐标系的ObXb轴固连在未变形柔性杆的中心轴线上。忽略中心刚体的形状尺寸，惯性坐标系的原点O0与浮动坐标系的原点Ob重合。惯性坐标系和浮动坐标系的夹角为θ。

中心刚体的转动惯量为Jh，作用在中心刚体上的控制力矩为τ。柔性杆的弹性模量为E，横截面积为A，截面惯性矩为I，密度为ρ，长度为L。末端质量为mp，不计末端质量的尺寸。

1.2 一次近似刚柔耦合动力学建模

图1中柔性杆中心轴线上距离原点x处的一点P0在柔性杆变形后为点P，点P0到点P的变形矢量在浮动坐标系下为up：

(1)

式中：u和v为变形矢量up在浮动坐标系下的分量;w1和w2为柔性杆轴向伸长量和横向变形量;由于柔性臂在运动时横向变形量远大于轴向伸长量;所以取v=w2。wc为柔性杆横向变形量引起轴向收缩量，为柔性杆横向变形量与纵向变形量的二次耦合项，在传统的零次近似模型中，这一项被忽略。wc表示为

(2)

柔性杆上的点P0在浮动坐标系ObXbYb下的位置矢量为ra=[x，0]T，则柔性杆变形后点P在惯性坐标系下的位置矢量为rp=Ts(ra+up)，其中Ts为浮动坐标系到惯性坐标系的转换矩阵，Ts=[cosθ，-sinθ；sinθ，cosθ]。末端质量在浮动坐标系ObXbYb下的位置矢量为rb=[L，0]T，变形矢量为ub=[u(L，t)，v(L，t)]T，柔性杆变形后末端质量在惯性坐标系下的位置矢量为rm=Ts(rb+ub)。

柔性机械臂结构系统的动能Tsys主要由中心刚体的转动动能Tz、柔性杆的动能Tr和末端质量的动能Tm组成，即Tsys=Tz+Tr+Tm。则系统的动能Tsys为：

(3)

式中:Jh为中心刚体的转动惯量，柔性杆轴线上点P在惯性坐标系下的位置矢量rp对时间的导数为：

(4)

末端质量在惯性坐标系下的位置矢量rm对时间的导数为：

(5)

柔性机械臂结构系统的势能Usys主要为柔性杆的变形能，Usys可以表示为：

(6)

通过系统动能和势能的表达式，可以得到系统动能的变分δTsys和势能的变分δUsys。系统的控制力矩为τ，系统的外力做功为Wf=τθ，则系统外力做功的变分为δWf=τδθ。由哈密尔顿原理，得到：

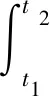
(7)

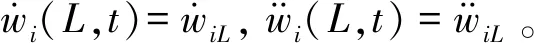
(9)

(10)

并得到一次近似刚柔耦合动力学方程在柔性杆两端的边界条件为：

其中B(x，t)为：

1.3 有限元离散动力学方程

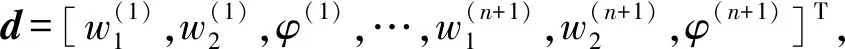
(11)

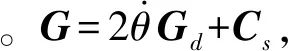
2 非惯性系下柔性机械臂动力学模型

在大多数情况下，由于中心刚体的转动惯量远大于柔性杆和末端质量的转动惯量，所以忽略机械臂柔性变形对系统转动的影响，即假设柔性机械臂系统的运动规律是事先已知的。在柔性机械臂的转动规律事先确定的时候，去掉方程(11)中的第一行，即得到非惯性系下柔性机械臂的动力学模型为：

(12)

式(12)为非惯性系下一次近似刚柔耦合动力学模型，将方程(12)中与柔性杆横向变形量和纵向变形量的二次耦合项wc有关的项设为0即可得到传统的零次刚柔耦合模型。

3 数值仿真

3.1 柔性机械臂运动规律

柔性机械臂转动的角度为θ，角速度为ωa，角加速度为αa，柔性机械臂转动角速度的规律设置如图2所示。柔性机械臂先加速到角速度为ωa=ωa0，然后以ωa0的角速度匀速转动，最后减速到角速度为0。如图2所示，柔性机械臂加速转动的时间为tacc，匀速转动的时间为tcon，最后减速转动的时间为tdec，柔性机械臂转动的时间总共为tm=tacc+tcon+tdec。

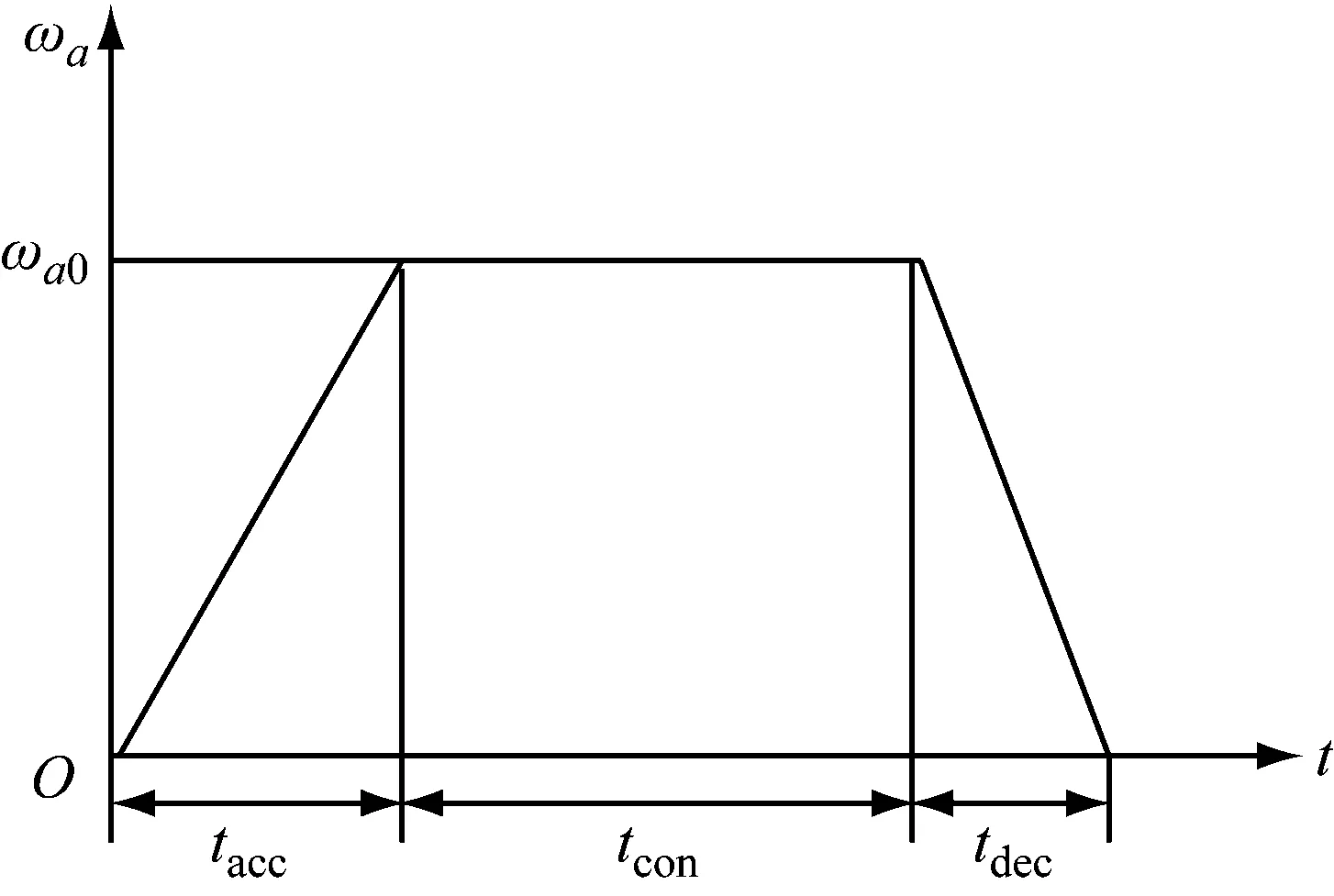
图2 柔性机械臂运动规律Fig.2 Motion profile of the flexible manipulator

当匀速转动的时间tcon>0时，柔性机械臂为梯形运动规律，当匀速转动的时间tcon=0时，柔性机械臂为三角形运动规律。柔性机械臂转动的角度为θm，即图2中柔性臂角速度曲线与时间轴所围成图形的面积。对于给定的转动角度，匀速转动的角速度ωa0=θm/(0.5tacc+tcon+0.5tdec)。柔性机械臂在各段时间转动的角速度ωa和角加速度αa为：

对于给定的旋转任务，即在一定的时间内柔性臂完成指定的旋转角度，通过调节减速段的时间可以在一定程度上控制柔性臂旋转后的残余振动。柔性机械臂的仿真参数如表1所示。

表1 柔性机械臂仿真参数Tab.1 Simulation Parameters of flexible manipulator

用表1的参数对静止时的柔性机械臂进行模态分析，得到柔性机械臂静止时的前两阶固有频率分别为f1=3.755 Hz，f2=30.991 Hz。用商业软件ANSYS对静止时的柔性机械臂进行模态分析，得到柔性机械臂的前两阶固有频率分别为f1=3.753 Hz，f2=31.478 Hz，与前面计算得到的固有频率基本接近，验证了本文所建立有限元模型的准确性。设ζ为柔性臂的模态阻尼比，取值通常在0.03～0.05之间，则瑞利阻尼系数为b1=4π*f1*f2*ζ/(f1+f2)，b2=ζ/π/(f1+f2)。取模态阻尼比ζ为0.03，则得到瑞利阻尼系数,如表1所示。

3.2 残余振动控制数值仿真

在柔性机械臂的自由振动中，柔性臂的第一阶振动占据主要成分，柔性机械臂第一阶振动的周期T1=1/f1，设Th=T1/8。在仿真过程中设定柔性机械臂转动角度为θm=60°，转动时间为tm=2 s，仿真时间为4 s，在转动时间tm结束后，即仿真时间在2 s～4 s时间内主要为系统的残余振动。为了研究柔性臂在给定图2所示的运动规律时，不同的加速转动时间tacc、匀速转动时间tcon和减速转动时间tdec对系统运动结束后残余振动的影响，对不同的时间分配情况分别进行仿真。由于柔性机械臂的总转动时间tm一定，所以加速转动时间tacc、匀速转动时间tcon和减速转动时间tdec三个变量中只有两个变量独立，本文设置不同的匀速转动时间tcon和减速转动时间tdec，在给定tcon和tdec时，加速转动时间tacc可以求出。

首先研究在不同的减速转动时间tdec情况下系统的残余振动情况，设置匀速转动时间tcon=0 s，即柔性机械臂为三角形转动规律，设置tdec=Th，用一次近似刚柔耦合模型对系统转动进行仿真，仿真得到柔性杆末端的横向变形w2和横向变形的加速度a2随时间变化规律,如图3和图4所示。

由图3和图4可以看出，当tdec=Th时在柔性机械臂转动结束后，柔性机械臂出现较大的残余振动，残余振动的振动周期为T1。柔性机械臂振动变形的最大峰值的绝对值用Am表示，Am出现的时间为ta，由图3可以看出，当tdec=Th时Am出现在2 s后，即系统转动结束后。为了描述系统转动结束后残余振动的大小，以2 s后系统振动的第一个峰值的绝对值Ah来表示残余振动的大小。

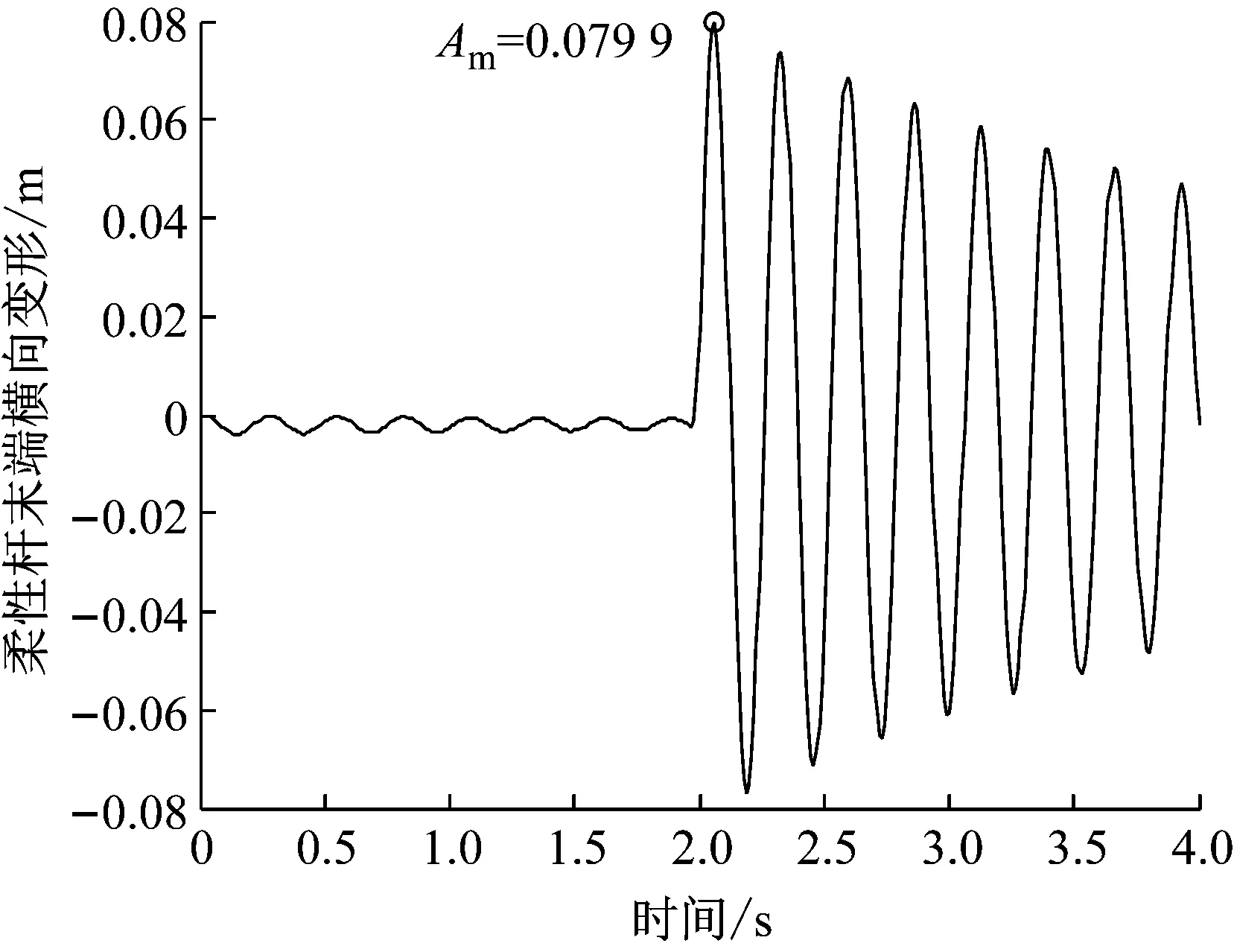
图3 柔性杆末端的横向变形(tdec=Th)

Fig.3 The transverse deformation of the flexible beam tip (tdec=Th)

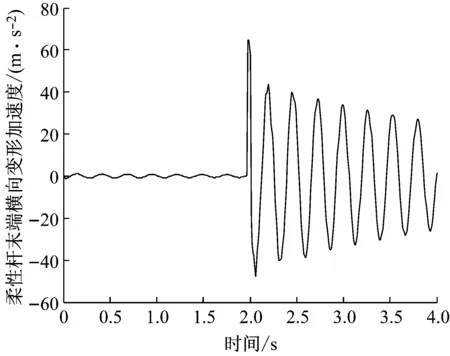
图4 柔性杆末端的横向变形的加速度(tdec=Th)

Fig.4 The transverse deformation acceleration of the flexible beam tip (tdec=Th)

当tdec=8Th时，用一次近似刚柔耦合模型对系统进行仿真，仿真得到柔性杆末端的横向变形w2和横向变形的加速度a2随时间变化规律如图5和图6所示。对比图3和图5可以看出，当tdec=8Th时系统振动变形的峰值Am出现在系统转动结束之前，并且此时Am的值为0.032 6 m，小于减速时间为Th时Am的值0.079 9 m。系统转动结束后残余振动的第一个峰值绝对值Ah为0.003 8 m，远小于减速时间为Th时Am的值0.079 9 m。当系统转动刚结束时，由图6可以看出系统的残余振动中有高阶振动分量，但是高阶振动在系统残余振动中占据成分很少，并且高阶振动分量衰减很快。对比图4和图6可以看出，减速时间tdec为8Th时比减速时间tdec为Th时，柔性杆末端振动变形的加速度得到了很大的降低。综合图5和图6可以看出，当减速时间为8Th时，系统的残余振动得到了较大程度的抑制。

图5 柔性杆末端的横向变形(tdec=8Th)

Fig.5 The transverse deformation of the flexible beam tip (tdec=8Th)

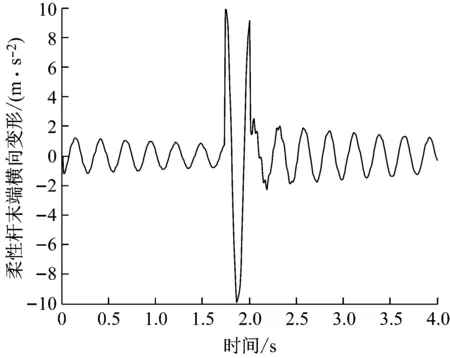
图6 柔性杆末端的横向变形的加速度(tdec=8Th)

Fig.6 The transverse deformation acceleration of the flexible beam tip (tdec=8Th)

设置减速转动时间tdec=i*Th，其中i=1，2，…，20。由于系统的总转动时间和总转动角度相同，匀速转动的时间为0，所以在不同的减速时间情况下，系统的最大转速ωa0相同。在设置不同的减速时间tdec情况下，系统振动变形的最大峰值Am以及它出现的时间ta如图7所示。由图7可以看出，在tdec≤4Th时，系统振动变形的最大峰值Am出现在系统转动结束后，当tdec>4Th时，系统振动变形的最大峰值Am出现在系统转动结束前。随着tdec的增加，Am出现的时间ta逐渐减小，并且Am的值总体上先大幅减小后缓慢减小。在tdec处于12Th到16Th之间，Am的值变化平缓。系统残余振动最大峰值的绝对值Ah与减速时间tdec的关系如图8所示。由图8可以看出当减速时间tdec=8Th和16Th时，残余振动的最大峰值Ah达到局部最小，当tdec=8Th时，Ah的值为0.003 8 m大于当tdec=16Th时Ah的值0.003 0 m。由图8可以知道随着减速时间的增加残余振动在整体上呈减小趋势。

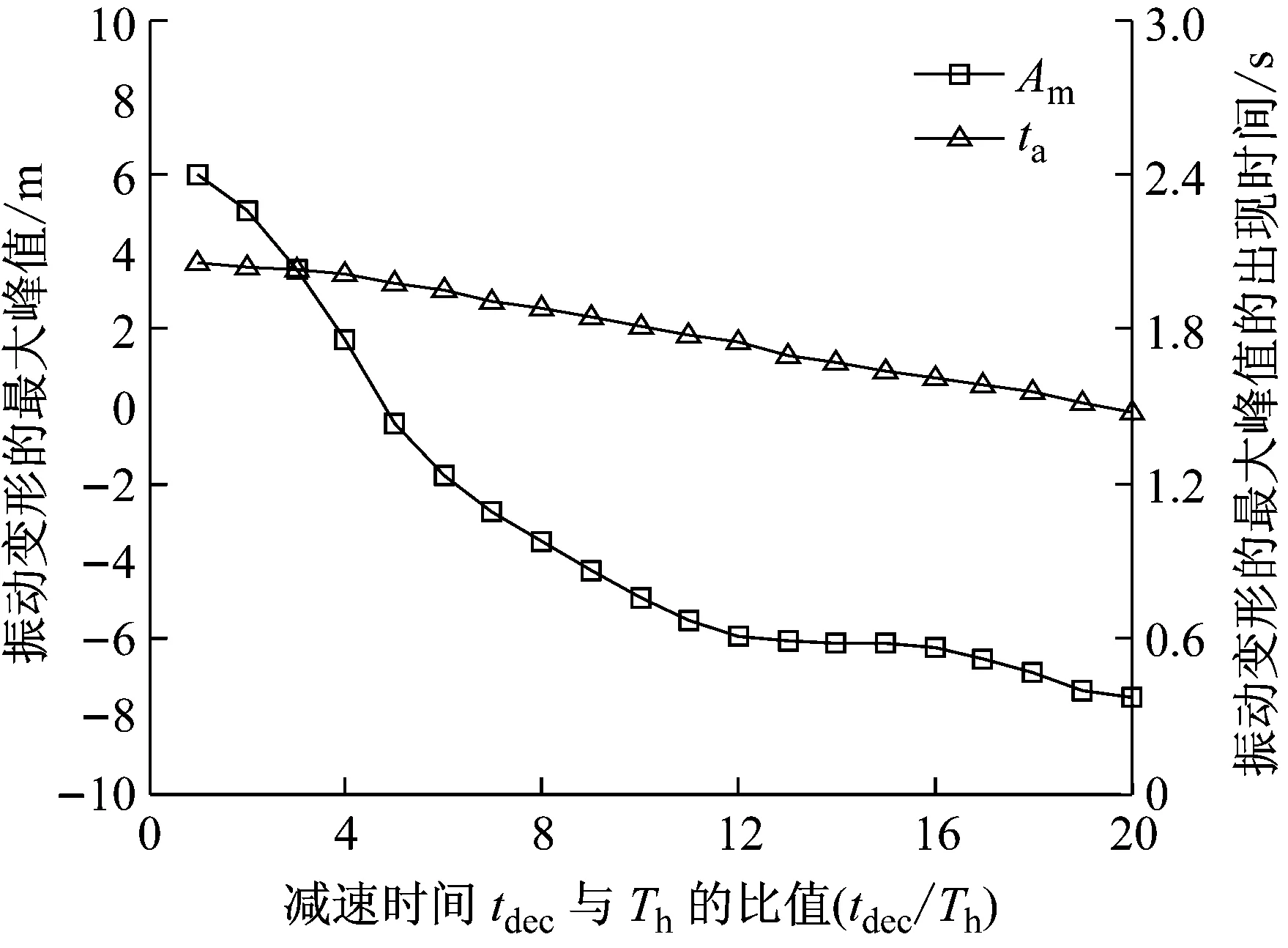
图7 最大峰值Am以及Am出现时间ta随减速时间的变化

Fig.7 The maximum peakAmand timetavary with the deceleration time

图8 残余振动最大峰值Ah随减速时间的变化Fig.8 The residual vibration peak Ah vary with the deceleration time

为了研究不同的匀速转动时间对系统残余振动的影响，设置减速时间tdec为8Th，设置匀速转动时间tcon=i*Th，其中i=0，1，…，20。当设置的匀速转动时间tcon逐渐增大时，系统的最大转速逐渐减小。系统残余振动最大峰值的绝对值Ah与匀速转动时间tcon的关系如图9所示。由图9可以看出，系统残余振动随着匀速转动时间的变化而波动变化，当匀速转动时间tcon=2Th、10Th和18Th时，残余振动峰值Ah达到局部极小。

4 结 论

本文用一次近似刚柔耦合模型对柔性机械臂进行了建模，并得到了在非惯性系下柔性机械臂的动力学模型。当柔性机械臂为三角形和梯形运动规律时，针对不同的运动参数设置，用所建立的一次刚柔耦合模型对柔性臂系统进行了仿真，主要得出以下结论：

(1) 当系统的减速时间相对系统的一阶振动周期较小时，系统转动后残余振动的幅值较大。当系统的减速时间等于系统的一阶振动周期，系统的残余振动得到了很好地抑制。在系统转动刚结束时，残余振动中含有高阶振动分量，但高阶振动在残余振动中分量占比较小，并且很快衰减。

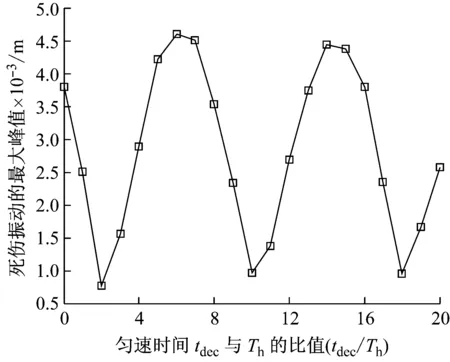
图9 残余振动最大峰值Ah随匀速时间的变化Fig.9 The residual vibration peak Ah vary with the constant speed time

(2) 当匀速转动时间不变时，随着设置的减速时间的增加，系统振动变形的最大峰值逐渐减小，出现的时间逐渐提前，当减速时间处于12Th到16Th之间，振动变形的最大峰值变化平缓。当减速时间等于8Th和16Th时，即减速时间等于柔性臂一阶振动周期的整数倍时，残余振动的最大峰值达到局部极小。

(3) 当减速时间不变时，随着匀速转动时间的增加，系统最大残余振动变形波动变化。当匀速转动时间等于2Th、10Th和18Th时，即匀速转动时间等于柔性臂一阶振动周期的1/4，或者等于一阶振动周期的1/4与一阶振动周期的整数倍的和时，残余振动峰值达到局部极小。