非均匀压电薄板面内自由振动的精确解

刘宗民， 张 健， 宋海燕

(哈尔滨工程大学 航天与建筑工程学院，哈尔滨 150001)

板的面内振动发生在平行于板平面的方向上，因其振动频率一般远高于通常的激励频率，所以相对于发生在垂直于板平面方向的横向振动而言，关于板面内振动的研究是很少的。虽然面内振动的早期研究可以追溯到19世纪Rayleigh的开拓性工作[1]，但一百多年来面内振动的研究一直处于停滞状态。近年来，随着高速飞行器和高速舰船的不断发展，以及直线型压电超声电机的研制，面内振动问题显得尤为突出，板的面内振动问题逐渐成为当前工程领域研究的热点，并引起国内外学者的广泛关注。

邢誉峰、刘波[2-4]指出，行驶中的船舶或飞行器在外界快速流动流体的激励下，会发生面内振动，并采用空间坐标分离变量方法(非逆法)给出了板壳在简支和固支边界任意组合情况下自由振动的封闭(非级数)形式精确解。刘剑等[5]指出，利用面内振动模态是直线型超声电机发展的主流。通过其结构的合理设计，在这种新型直线型超声电机中，矩形压电陶瓷薄板既充当了把电能向机械能转换的角色，又充当了驱动振子(定子)的作用。Bardell等[6]采用瑞利-里兹方法计算了板面内自由振动的频率，并对面内振动的早期研究进行较为全面的梳理与评述。Gorman[7-9]采用叠加方法对自由、简支与固支边界条件下的矩形板面内自由振动问题进行了研究。Du等[10-11]采用改进的傅里叶级数方法分析了弹性支撑板的面内自由振动问题。裴然等[12]采用二维改进傅里叶级数方法研究了矩形板结构面内振动特性。王青山等[13]采用改进傅里叶级数法(Improved Fourier Series Method,IFSM) 对矩形板在任意边界下的面内自由振动特性进行了研究。Masahiro[14]对沿板厚方向极化的压电矩形板的面内振动进行了二维瞬态分析。

王保林等[15]指出，要得到非均匀材料的力学问题的精确解是非常困难的。本文假设压电材料参数沿厚度方向以同一指数形式变化，给出了非均匀压电薄板面内自由振动的基本方程。应用分离变量方法，对四边简支非均匀压电薄板的面内自由振动的精确解进行了研究，并通过算例讨论了相关问题。邢誉峰等提出的分离变量方法，是一个研究面内自由振动精确解的行之有效的方法，本文在以往弹性薄板面内自由振动精确解研究的基础上，将面内自由振动精确解的研究拓展到了非均匀压电薄板，这既是对以往研究的发展，同时也会促进面内自由振动在非均匀材料力学领域的研究。

1 基本方程

非均匀压电薄板的基本方程为

本构关系

(1)

几何方程

(2)

考虑到压电板很薄(h/ai≪1)，所以可以用应力沿厚度的平均值描述压电薄板的应力状态[16]，即

(3)

将式(1)和(2)代入(3)，可得恒定电场下非均匀压电薄板的面内自由振动微分方程

(4)

面内自由主振动可以写成

(5)

把式(5)代入式(4)可得

(6)

第一种边界条件SS1[2]：

(7)

第二种边界条件SS2[2]：

(8)

式中

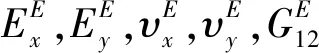
2 精确解

式(5)分离变量形式的精确解为

(9)

式中

φ1=A1cos(Ωx)+A2sin(Ωx),

φ2=A3cos(Λx)+A4sin(Λx),

ψ1=B1cos(Ty)+B2sin(Ty),

ψ2=B3cos(Zy)+B4sin(Zy)

将边界条件(7)和(8)代入式(9)，可得相应的本征函数和本征方程，如表1和表2所示。

表1对边x=0和a为SS1和SS2的四种组合及对应的本征函数和本征值方程

Tab.1Theeigenvalueequationsandeigenfunctionsforthesimplesupportoppositeedgesx=0，a

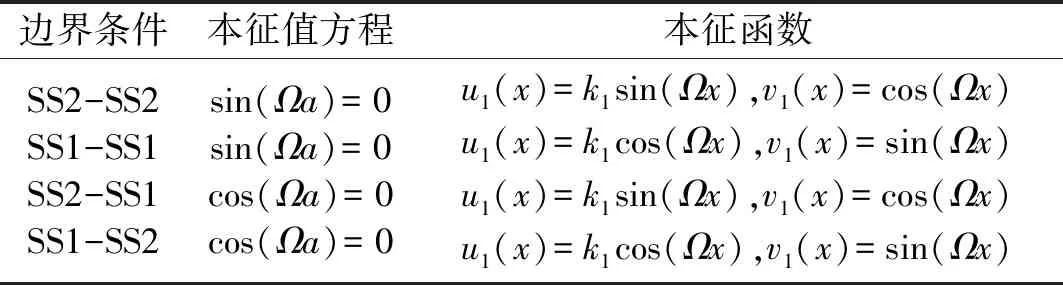
边界条件本征值方程本征函数SS2-SS2SS1-SS1SS2-SS1SS1-SS2sin(Ωa)=0sin(Ωa)=0cos(Ωa)=0cos(Ωa)=0u1(x)=k1sin(Ωx),v1(x)=cos(Ωx)u1(x)=k1cos(Ωx),v1(x)=sin(Ωx)u1(x)=k1sin(Ωx),v1(x)=cos(Ωx)u1(x)=k1cos(Ωx),v1(x)=sin(Ωx)

两种简支边界条件在四条边上有6种不同的组合，分别为:SS1-SS1-SS1-SS1，SS2-SS2-SS2-SS2，SS1-SS2-SS2-SS2，SS1-SS1-SS2-SS2，SS1-SS2-SS1-SS2， SS1-

表2对边y=0和b为SS1和SS2的四种组合及对应的本征函数和本征值方程

Tab.2Theeigenvalueequationsandeigenfunctionsforthesimplesupportoppositeedgesy=0，b

边界条件本征值方程本征函数SS2-SS2SS1-SS1SS2-SS1SS1-SS2sin(Tb)=0sin(Tb)=0cos(Tb)=0cos(Tb)=0u2(y)=cos(Ty),v2(y)=k3sin(Ty)u2(y)=sin(Ty),v2(y)=k3cos(Ty)u2(y)=cos(Ty),v2(y)=k3sin(Ty)u2(y)=sin(Ty),v2(y)=k3cos(Ty)

SS1-SS1-SS2。

由表1和表2可知SS1-SS1-SS1-SS1板的本征函数为

U(x,y)=k1cos(Ωx)sin(Ty)

V(x,y)=k3sin(Ωx)cos(Ty)

(10)

把式(10)代入式(6)，并整理可得

[(1+a1)Ω2+(1+a2)T2]β2+β4=0

(11)

由式(11)解出频率参数β，可得

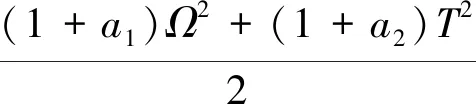
(12)

3 算 例

以四边简支(SS1-SS1-SS1-SS1)情况为例，非均匀压电矩形薄板厚度h=0.02 m，维度a×b=1 m×1.2 m。BaTiO3材料参数参照文献[17]。

当k的取值变化时，四边简支非均匀压电矩形薄板面内自由振动的频率,如表3所示。

表3 非均匀压电薄板面内自由振动频率Tab.3 Frequency for free in-plane vibrations of inhomogeneous rectangular piezoelectric plate

四边简支情况下，不均匀系数k与频率ω的关系,如图1所示。

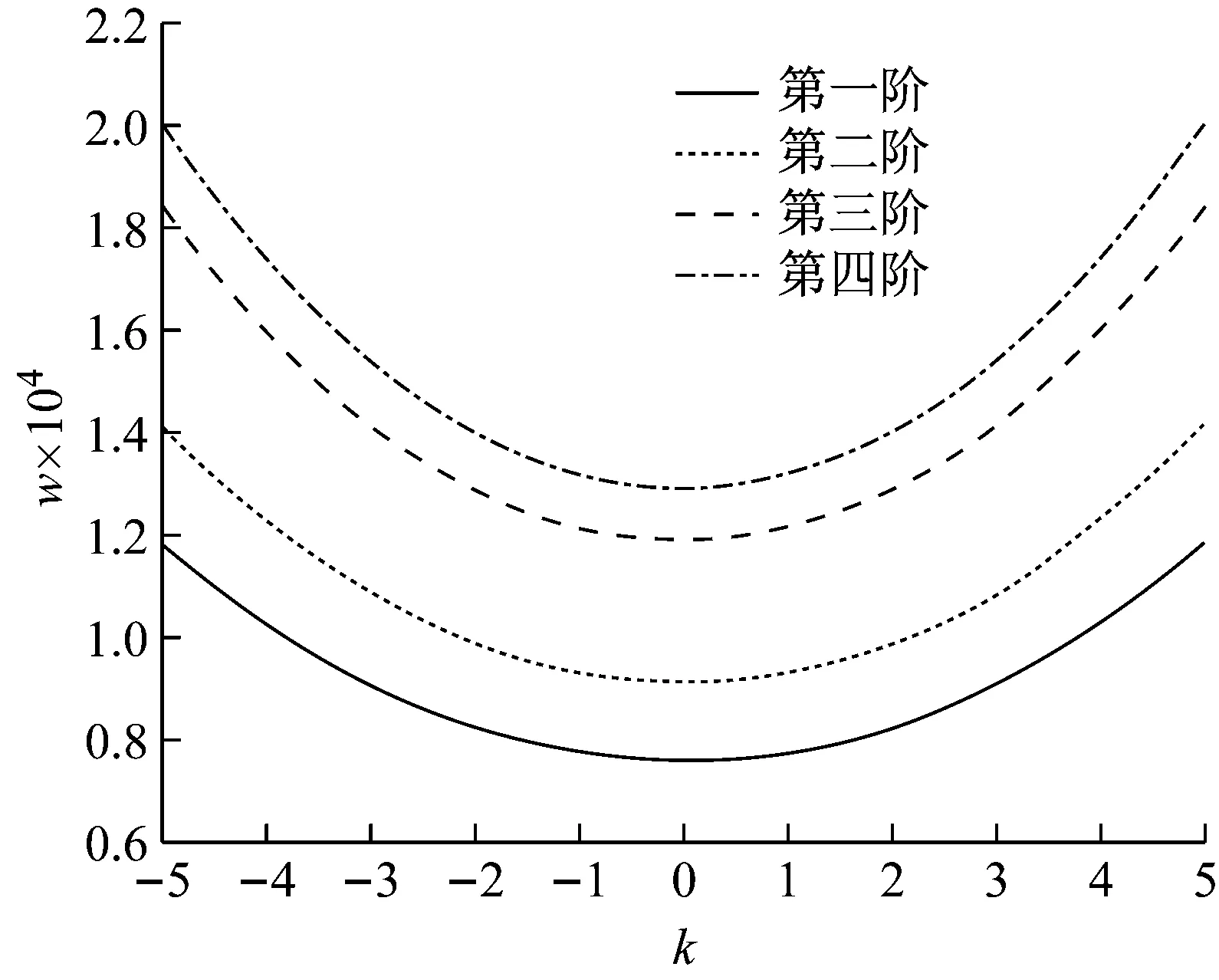
图1 不均匀系数k与面内振动频率ω的关系图Fig.1 The relationship between non-uniform coefficient k and frequency for free in-plane vibrations ω

由图1可看出，当k取正数时，随着k值增大，频率

也随之增大，频率增速由频率的阶数决定，阶数越高，频率增长的越快；当k取负数时，随着k值减小，频率随之增大，相应的增幅也越快。当选取SS2-SS2-SS2-SS2，SS1-SS2-SS2-SS2，SS1-SS1-SS2-SS2，SS1-SS2-SS1-SS2，SS1-SS1-SS1-SS2这5种四边简支情况时，也可以得到如上结论。

四边简支情况下，前四阶振型,如图2所示。

将非均匀压电薄板退化为非均匀弹性薄板，当k的取值变化时，四边简支非均匀弹性薄板面内自由振动的频率,如表4所示。

当k=0时，η*(0)=1，非均匀弹性薄板退化为均匀弹性薄板，频率参数β,如表5所示。

由表5可以看出，四边简支均匀弹性薄板面内自由振动频率参数β与文献[2,18]的结果相差很小,可以证明本文所给精确解的正确性。

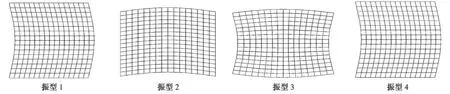
(a) SS1-SS1-SS1-SS1前四阶振型图

(b) SS2-SS2-SS2-SS2前四阶振型图

(c) SS1-SS2-SS1-SS1前四阶振型图

(d) SS1-SS2-SS2-SS1前四阶振型图

(e) SS1-SS2-SS1-SS2前四阶振型图

(f) SS1-SS2-SS2-SS2前四阶振型图图2 四边简支情况前四阶振型图Fig.2 The fourth order vibration modes of simply supported表4 非均匀弹性薄板面内自由振动频率Tab.4 Frequency for free in-plane vibrations of inhomogeneous rectangular elastic plate

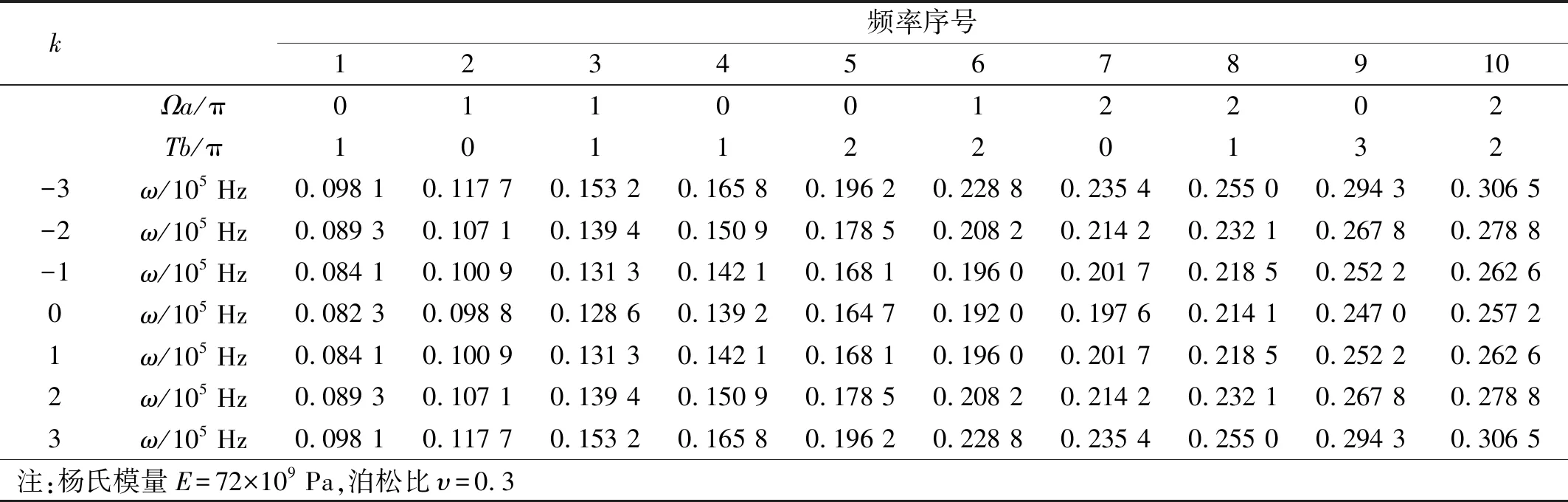
k频率序号12345678910Ωa/π0110012202Tb/π1011220132-3ω/105 Hz0.098 10.117 70.153 20.165 80.196 20.228 80.235 40.255 00.294 30.306 5-2ω/105 Hz0.089 30.107 10.139 40.150 90.178 50.208 20.214 20.232 10.267 80.278 8-1ω/105 Hz0.084 10.100 90.131 30.142 10.168 10.196 00.201 70.218 50.252 20.262 60ω/105 Hz0.082 30.098 80.128 60.139 20.164 70.192 00.197 60.214 10.247 00.257 21ω/105 Hz0.084 10.100 90.131 30.142 10.168 10.196 00.201 70.218 50.252 20.262 62ω/105 Hz0.089 30.107 10.139 40.150 90.178 50.208 20.214 20.232 10.267 80.278 83ω/105 Hz0.098 10.117 70.153 20.165 80.196 20.228 80.235 40.255 00.294 30.306 5注:杨氏模量E=72×109 Pa,泊松比υ=0.3

表5 均匀弹性薄板面内自由振动频率参数Tab.5 Frequency parameters for free in-plane vibrations of homogeneous rectangular elastic plate

4 结 论

本文假设压电材料参数沿厚度方向以同一指数形式变化，给出了非均匀压电薄板面内自由振动的基本方程。应用分离变量方法，给出了四边简支非均匀压电薄板面内自由振动的精确解。

分析了非均匀压电薄板的不均匀系数与面内自由振动频率之间变化规律。在四边简支情况下，当不均匀系数取正数时，随着数值的增大，频率也随之增大，频率增速由频率阶数决定，阶数越高，频率增长的越快；当不均匀系数取负数时，随着数值的减小，频率随之增大，频率增速由频率阶数决定，阶数越高，频率增长的越快。研究表明非均匀压电材料可以通过调整材料的组成，使其动力学性能得以提高，从而满足结构特殊的功能需要。

将非均匀压电薄板退化为非均匀弹性薄板，得到四边简支非均匀弹性薄板面内自由振动频率。进一步将非均匀弹性薄板退化为均匀弹性薄板，得到四边简支均匀弹性薄板面内自由振动的频率参数，并验证了其精确解的正确性。