变步长频率加权能量算子在轴承故障诊断中的应用

刘泽潮， 林建辉， 丁建明, 吴文逸

(西南交通大学 牵引动力国家重点实验室， 成都 610031)

轴承是列车走行部中的关键部件，它的运行状态与列车的运行安全息息相关。轴承的状态监测可以采用温度、声学、振动等多种方式检测方式。然而，轴承温度的检测具有滞后性，而声学检测易受环境噪声干扰。所以，基于振动的故障诊断方法被广泛应用于轴承的状态监测[1]。

当轴承发生磨损、疲劳剥落、划痕等故障时，轴承会产生周期性冲击。这些周期性冲击会激起机械系统的高频振荡，通过对高频振荡信号的解调可以实现故障早期微弱特征的提取。基于希尔伯特变换的包络解调是一种常用的解调算法，通过分析其频谱从而可以实现故障的诊断与识别[2]。然而，希尔伯特变换存在它的局限性：一是容易受到其他频率的干扰；二是在计算瞬时能量时，其只保留了瞬时幅值，而忽略了瞬时频率的影响[3-5]。所以，为了更好的提取冲击的周期成分，Teager-Kasier 能量算子(TEO)被用于进行信号的解调。Teager算子解调相较于包络解调具有更好的抗干扰特性[6-10]。但是，Teager算子作为一种能量算子不应当存在无意义的负值，所以John提出了一种类似的算子，频率加权能量算子(FWEO)[11]。相比较于Teager算子解调，FWEO算子解调具有更强的抗干扰特性。FWEO算子通过计算信号导数的包络来实现信号的解调。对于离散信号，在计算导数时包括多种差分方式：前向差分方式、后向差分方式和中间差分方式。FWEO算子使用了中间差分方式。但是研究发现，当解调信号的中心频率较低时，其相邻采样点的数值相近。这就导致FWEO幅值较小，所以故障信息被噪声所淹没。

所以，提出改进的变步长频率加权能量算子(VFWEO)，该算法不仅具有FWEO算子优越的抗干扰特性，同时改善了其在中心频率较低时解调鲁棒性差的缺点。通过研究发现，改变步长参数可以实现针对不同共振频带的解调。同时，本文给出了针对不同共振频带中心步长参数的计算公式。通过仿真信号与实测信号表明，该解调算法可以有效的提取不同共振频带中心的特征频率信息，实现轴承的早期故障检测与诊断。

1 能量算子

1.1 Teager-Kasier 能量算子

Teager能量算子通常用于计算信号的瞬时能量，它克服了希尔伯特变换在计算瞬时能量时只考虑瞬时幅值而忽略瞬时频率的缺点。其表达式为：

(1)

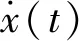
根据研究，震荡物体的信号为调幅-调频信号[11]，它的表达式为：

x(t)=Acos(ωt+φ)

(2)

式中：A为幅值；ω为震荡的固有频率；φ为初始相位。

(3)

(4)

将式(2)～(4)代入式(1)可得式(5)：

(5)

式(1)的离散形式为：

ψ[x(n)]=[x(n)]2-x(n+1)x(n-1)

(6)

1.2 频率加权能量算子

因为包络解调与Teager算子解调容易受到干扰信号的影响，所以提出了频率加权能量算子。频率加权能量算子通过计算信号导数的包络来计算调制信号的瞬时能量,实现解调。频率加权能量算子的表达式为：

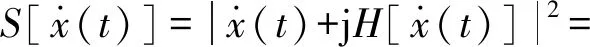
(7)

式中：S[·]表示包络；H[·]表示希尔伯特变换；Γ[x(t)]为频率加权能量算子。

根据式(2)则

(8)

(9)

将式(8)和式(9)代入式(7)可得

Γ[x(t)]=(-Aωsin(ωt+φ))2+

(Aωcos(ωt+φ))2=A2ω2

(10)

因此，表明频率加权能量算子在计算瞬时能量时具有同Teager算子相似的性质。

对比式(1)与式(7)，Teager能量算子与频率加权能量算子的区别主要是在第二部分。为了对比第二部分在解调时对频谱的影响，分别计算第二部分对应的傅里叶谱：

*X(ω)

(11)

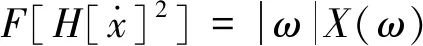
(12)

式中：F[·]表示傅里叶变换；X(ω)表示x(t)的傅里叶谱；*表示卷积操作。

为了得到频率加权能量算子的离散形式，在计算导数时，使用了中点平均差分方式：

(13)

(14)

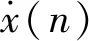
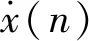
2 变步长频率加权能量算子

2.1 基本原理

因此为了克服FWEO的缺点，在频率加权能量算子的基础上提出了变步长频率加权能量算子(VFWEO)，使用变步长差分公式代替中间差分公式。变步长差分表达式为

(15)

(16)

式中：l为步长参数。

则VFWEO可以表示为：

h(n+l)h(n-l)]

(17)

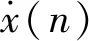
因此，可以看出步长参数l的取值对VFWEO解调效果的影响至关重要。通过调节步长参数，使得公式(15)的取值变大，此时VFWEO的解调效果更好。

2.2 步长参数计算

如式(17)所示，步长参数l对VFWEO算子的解调效果具有重要影响。通过调节步长参数，可以使得VFWEO针对不同中心频率的故障冲击信号都可以得到较好的解调效果。因此，步长参数与中心频率的关系对保证VFWEO的解调效果至关重要。

式(2)的离散形式如下所示：

x(n)=Acos(ωn+φ)

(18)

式中：A为幅值，ω=2πfC/fS为角频率，其中fC为调制信号的中心频率，fS为采样频率，φ为初始相位。

因为频率加权算子的核心是计算导数的包络，所以在保证信号的导数幅值最大时就可以保证更好的解调效果。

将式(18)代入式(15)，可以得到式(19)：

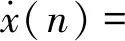
(19)

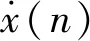
(20)

所以，当步长参数l与中心频率fc满足式(20)的关系式时，VFWEO的解调效果最好。这就说明通过调节不同的步长参数l使得VFWEO在对不同频率中心fC的调制信号进行解调时，都可以得到理想的解调效果，有效地提取出故障冲击。当计算得到的步长参数l为小数时，通过四舍五入取整。

3 仿真验证

为了验证VFWEO算子在强噪声环境下的鲁棒性，本文使用包络解调、Teager算子解调、FWEO算子解调与VFWEO算子解调的对包含噪声的轴承仿真信号进行分析。仿真信号的表达式为：

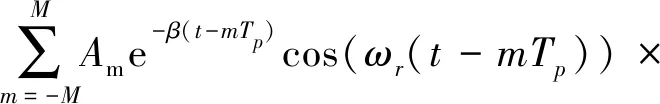
u(t-mTp)

(21)

式中:Am是冲击的幅值，Am=1；Tp是故障冲击的间隔，特征频率FCF=1/Tp=50 Hz；ωr是故障引起共振的频率，ωr=1 000 Hz；β是阻尼系数，β=1 500 N·s/m。

仿真信号的采样频率为20 kHz，信号长度为16 384个采样点。仿真信号加入SNR=-5 dB的白噪声和100 Hz与800 Hz的正弦干扰信号。仿真信号的时域波形、加噪信号的时域波形与频谱如图1所示。

如图1(c)所示，信号的共振频带在1 000 Hz附近。根据公式(20),计算所得步长参数l=5。四种解调算法的解调效果，如图2所示。

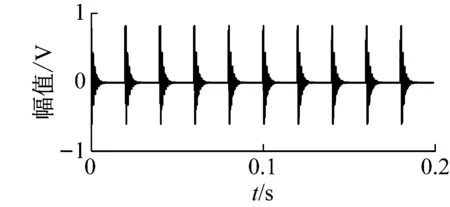
(a) 原始信号

(b) 加噪信号

(c) 加噪信号频率图1 仿真信号Fig.1 The simulated signal

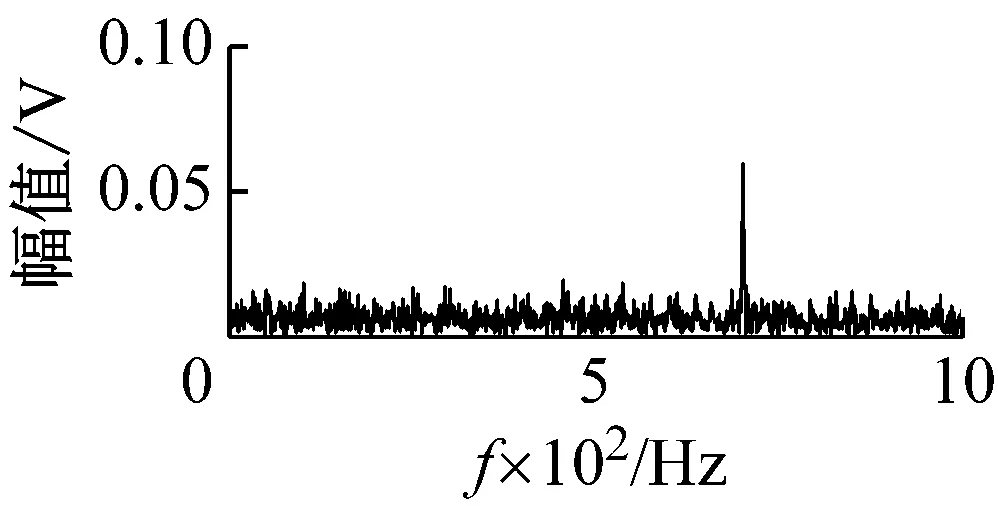
(a) 包络谱

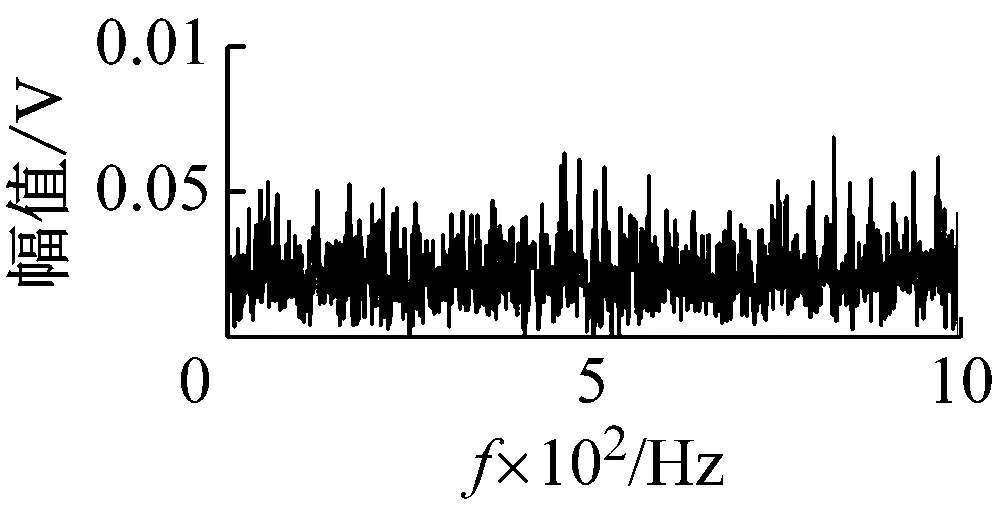
(b) Teager谱

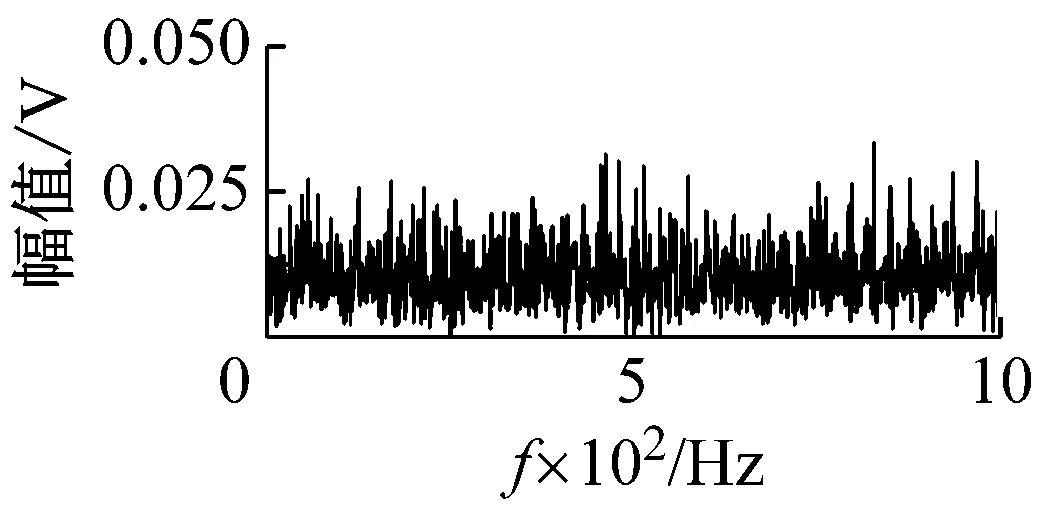
(c) FWEO谱

(d) VFWEO谱图2 不同算子解调效果对比Fig.2 Comparison of demodulation results of different operators

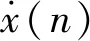
图3 不同步长参数的解调效果对比Fig.3 Comparison of demodulation results of different step parameters

为了验证式(20)所计算的最优步长参数具有最好的解调特性，计算了不同步长参数l对应的VFWEO谱。步长参数的取值范围为1～5，各个步长参数下的VFWEO谱如图3所示。当步长参数l=1时，VFWEO算子就是FWEO算子。此时，故障冲击被淹没于噪声之中。随着步长参数l的增加x(n+l)与x(n-l)的差值越来越大。因此，VFWEO对故障冲击的提取效果更好，所以特征频率及其倍频的幅值随着步长参数的增加而增加。当步长参数l=5时，无论是幅值还是谐波数量都达到最大。此时的解调效果最佳，其结果与式(20)计算相同。这就证明，通过调节步长参数可以增强与之对应的共振频带的解调效果。

研究发现，在进行解调时与步长参数l相对应的共振频带的幅值最大，而其它共振频带的幅值较小。通过调节步长参数可以实现特定频带的解调。为了验证VFWEO中步长参数针对不同共振频带的解调效果，本文构造了包含两个故障信息的轴承仿真信号，其表达式如式(21)所示。仿真信号的参数，如表1所示。

表1 仿真信号参数Tab.1 Parameters of simulated signals

加入SNR=-5的高斯白噪声，仿真信号的傅里叶谱，如图4所示。

从图4中可以看出，该仿真信号包含两个共振频带，中心频率分别在1 000 Hz和5 000 Hz附近。

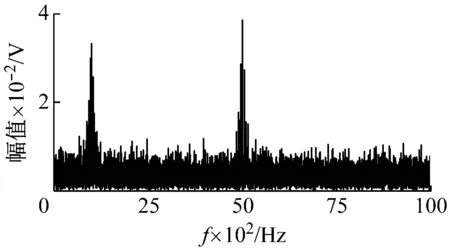
图4 仿真信号频谱Fig.4 The Fourier spectrum of simulated signal

根据式(20)计算可得，当步长参数l=1时，VFWEO对应中心频率为5 000 Hz的共振频带。其解调结果如下图5(a)所示，VFWEO谱中的主要为故障2的特征频率及其谐波。根据式(20)计算可得，当尺度参数l=5时，VFWEO对应的为中心频率为1 000 Hz的共振频带。其解调结果如下图5(b)所示，VFWEO谱中的主要为故障1的特征频率及其谐波。实验表明，通过调节步长参数从而实现了针对不同频带的解调。

(a) l=1

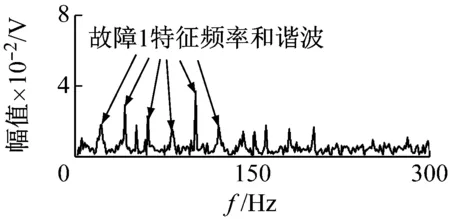
(b) l=5图5 VFWEO谱Fig.5 The VFWEO spectrum

4 实验验证

4.1 美国西储大学轴承数据库

美国西储大学轴承数据库作为一个标准的轴承故障诊断算法验证数据库，被广泛用于验证算法的有效性[12]。本文选用驱动端外圈故障信号，采样频率为12 kHz，数据长度为16 384个采样点，转速为1 730 r/min,外圈故障特征频率fBPFO=103.3 Hz。其实验装置，如图6所示。

实测信号如图7所示，分析实测信号的频谱可以发现共振频带主要集中在3 000 Hz附近。根据式(20)，计算可得步长参数l=1。此时，VFWEO算子与FWEO算子计算结果相同。

包络解调、Teager解调和VFWEO解调结果的频谱如下图8所示。包络谱、Teager和VFWEO谱中都可以发现很明显的轴承外圈故障的特征频率及其倍频。但是包络谱和Teager谱中的5倍频的幅值高于4倍频的幅值，而只有VFWEO谱中的倍频呈指数衰减。因此，VFWEO算子解调相比较于包络解调与Teager算子解调具有更好的解调效果。

图6 实验装置Fig.6 The experimental device

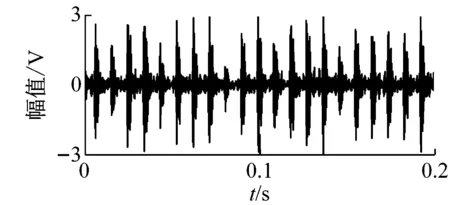
(a) 时域波形

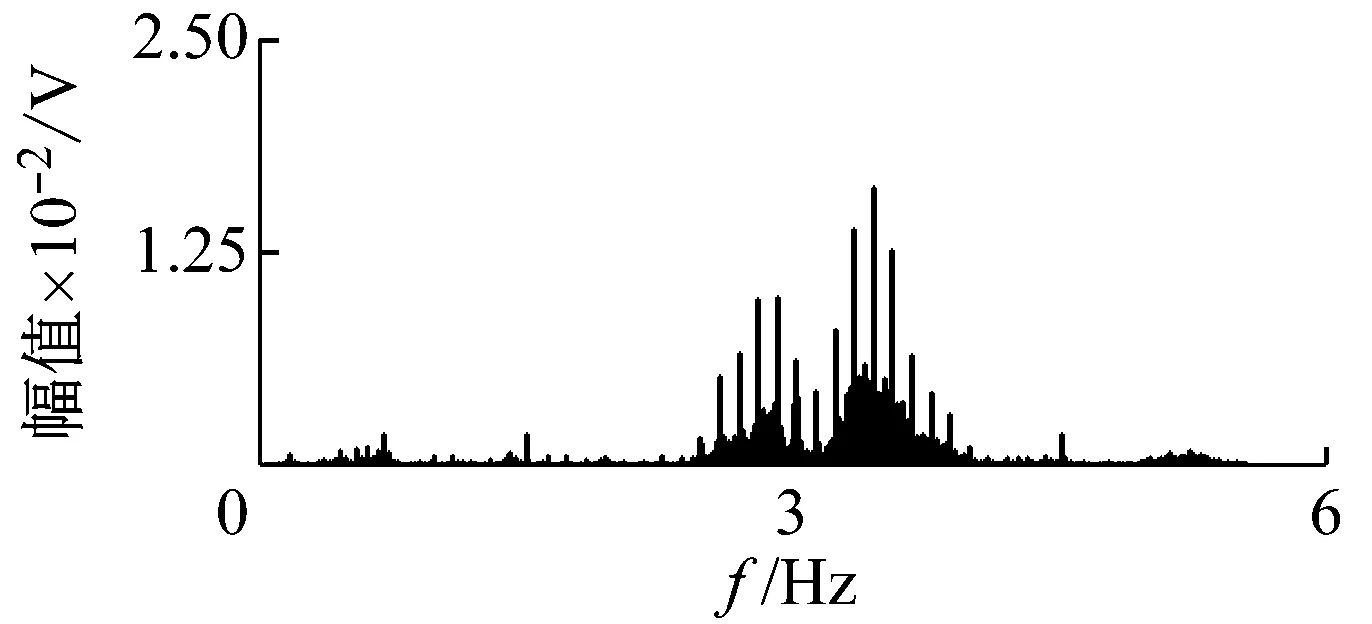
(b) 信号频谱图7 实测信号Fig.7 The measured signal

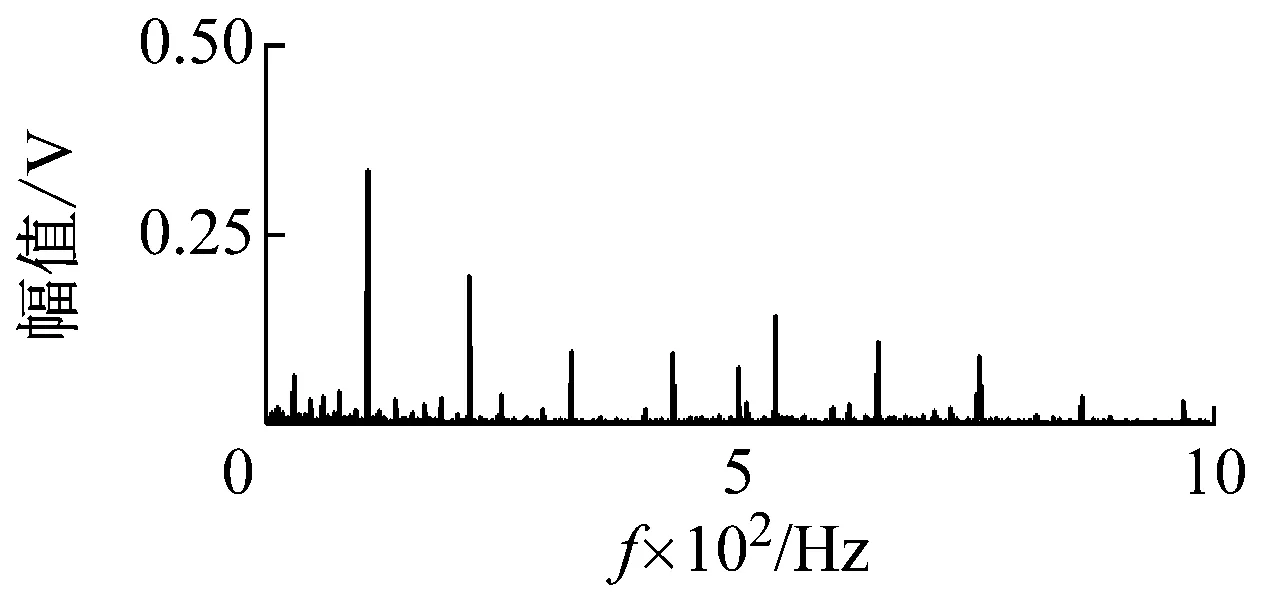
(a) 包络谱

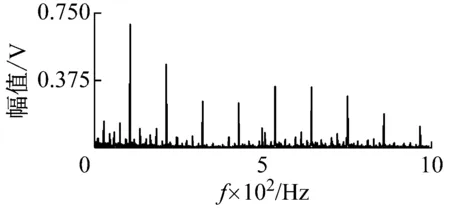
(b) Teager谱

(c) VFWEO谱图8 不同算子解调效果对比Fig.8 Comparison of demodulation results of different operators

4.2 高速列车轴箱轴承故障实验台

由于美国西储大学轴承数据库中的信号的信噪比较高且频谱成分较简单，所以几种传统的解调算法都可以实现特征频率的提取。为了进一步验证VFWEO算子针对不同频带的解调效果，本文使用高速列车轴箱轴承故障实验台的振动数据进行了进一步验证。实验装置，如图9所示。

图9 实验装置Fig.9 The experimental device

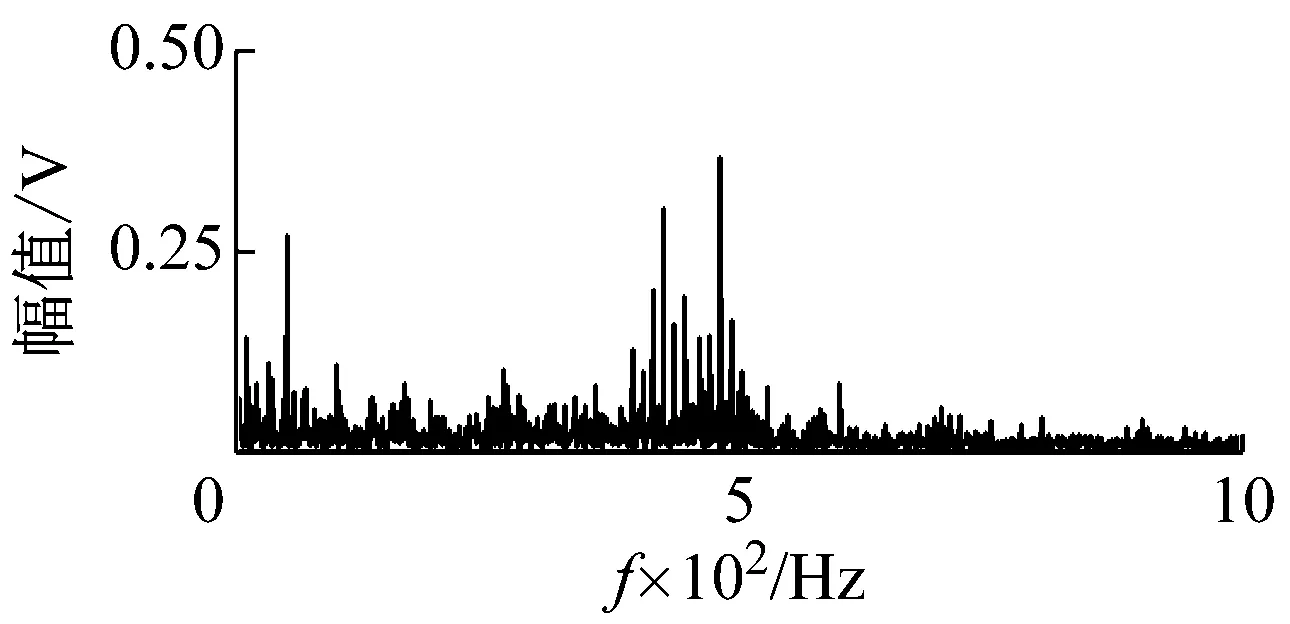
振动信号的采样频率为10 kHz，数据长度为16 384个采样点。轴承的故障类型为滚子故障，转动频率fr为5.1 Hz，特征频率fBSF为33.9 Hz。其振动信号的时域波形与频谱，如图10所示。

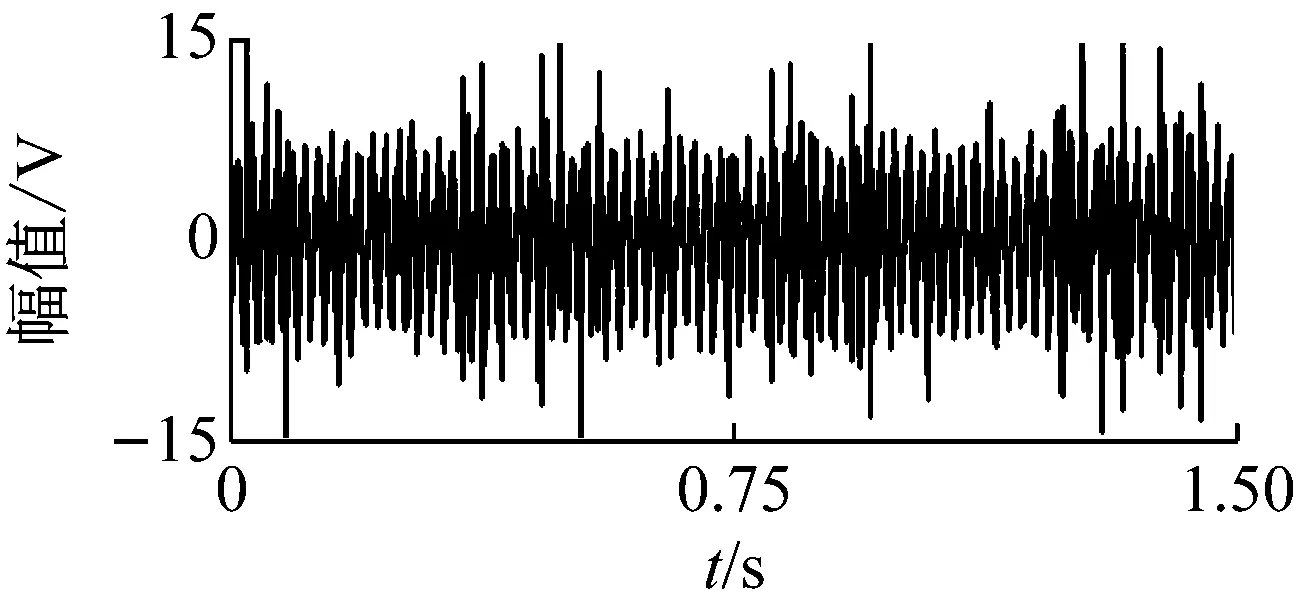
(a) 时域波形

(b) 信号频谱图10 实测信号Fig.10 The measured signal

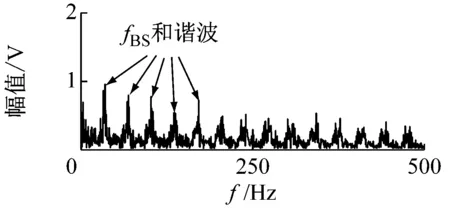
为了验证VFWEO的有效性，使用包络解调、Teager算子解调、FWEO算子解调与VFWEO算子解调对振动信号进行了分析。如图10(b)所示，实测信号存在三个可能的共振频带，它们的频带中心分别是大约：500 Hz、1 500 Hz和3 400 Hz。因此根据式(20)，它们分别对应的步长参数为：5、2和1。当步长参数l=1时，VFWEO简化为FWEO。包络解调与Teager算子解调的结果如图11所示。由于信号的频谱中包含多个共振频带与干扰，所以，包络解调无法解调出故障信息。而Teager算子由于其抗干扰性优于包络解调，所以可以解调出滚子的特征频率及其谐波。

(a) 包络谱

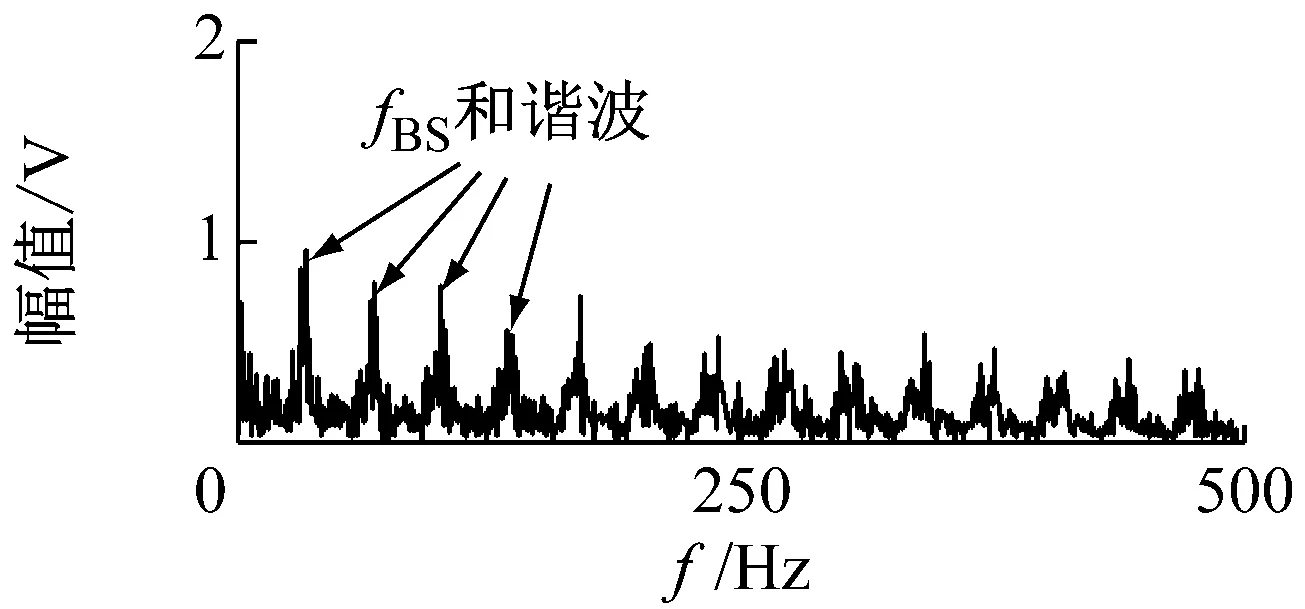
(b) Teager谱图11 传统算子解调Fig.11 The demodulation results of traditional operators

(a) l=1

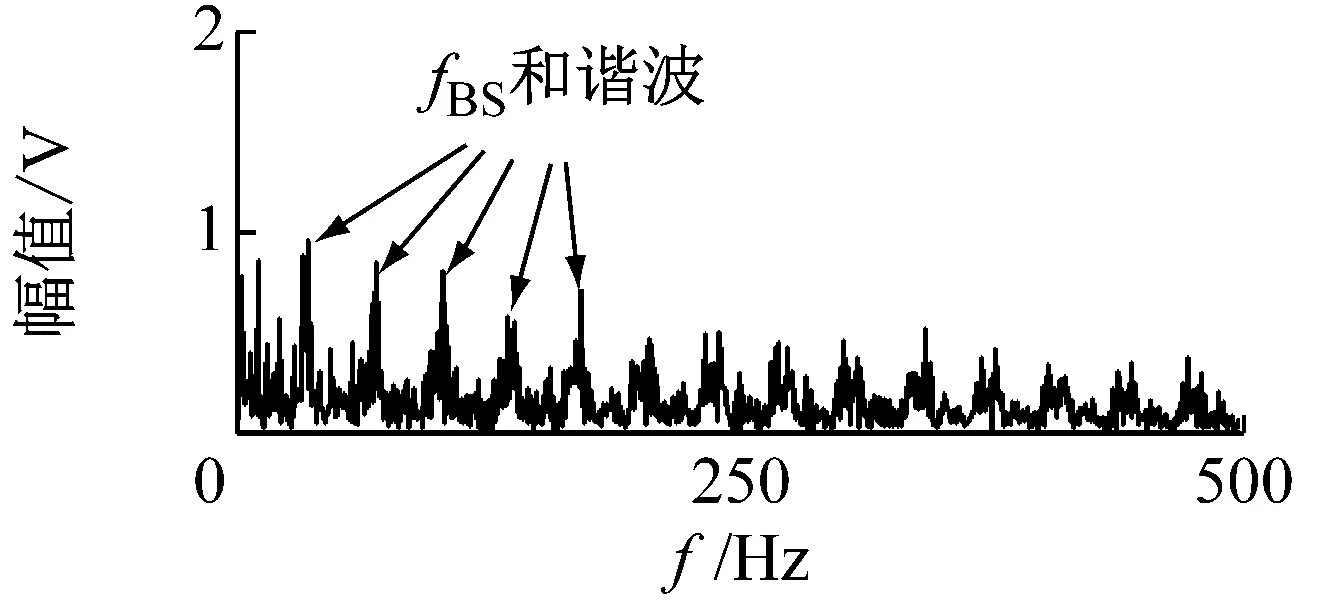
(b) l=2

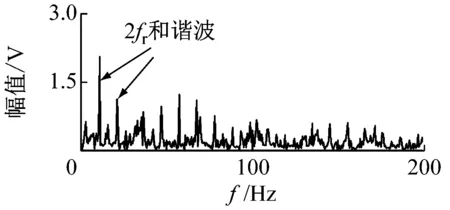
(c) l=5图12 VFWEO谱Fig.12 The VFWEO spectrum

如图12所示为不同参数下VFWEO谱。当步长参数l=1，2时，VFWEO可以解调出滚子故障的特征频率及其倍频；当步长参数l=5时，VFWEO可以解调出与转频有关的特征频率。所以，通过改变步长参数VFWEO可以实现针对不同频带的解调。为了进一步证明解调效果，使用经验小波变换与尺度空间表示对故障信号进行预处理[13-14]。通过尺度空间表示可以自适应的实现共振频带的划分，然后经验小波变换可以根据频带划分生成对应的滤波器组，这些滤波器组可以实现信号的自适应分解。通过尺度空间表示计算，信号的频谱及其频带划分，如图13所示。

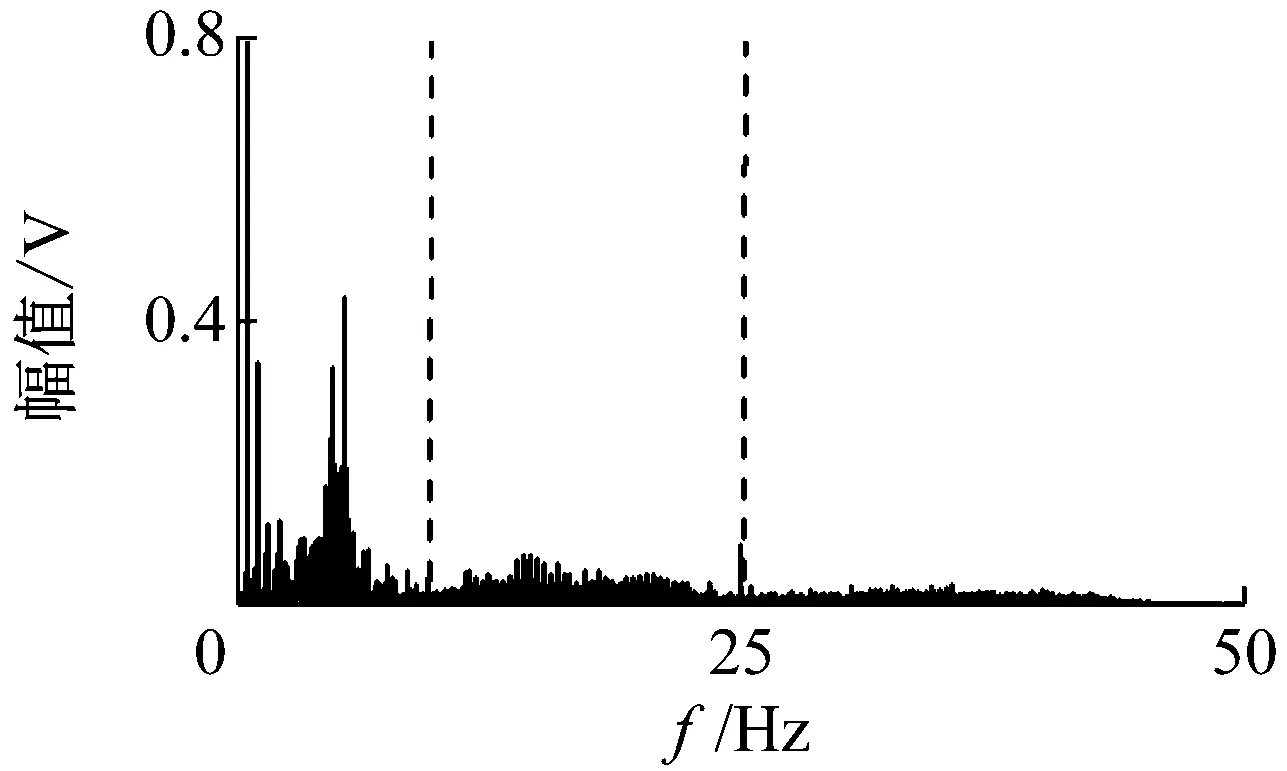
图13 频带划分Fig.13 Detected boundaries

根据如图13所示的频带划分,信号被分解成为三个分量，其对应的频带区间分别为:[0, 978 Hz]、[978 Hz, 2 524 Hz]和[2 524 Hz, 5 000 Hz]。它们的包络谱，如图14所示。

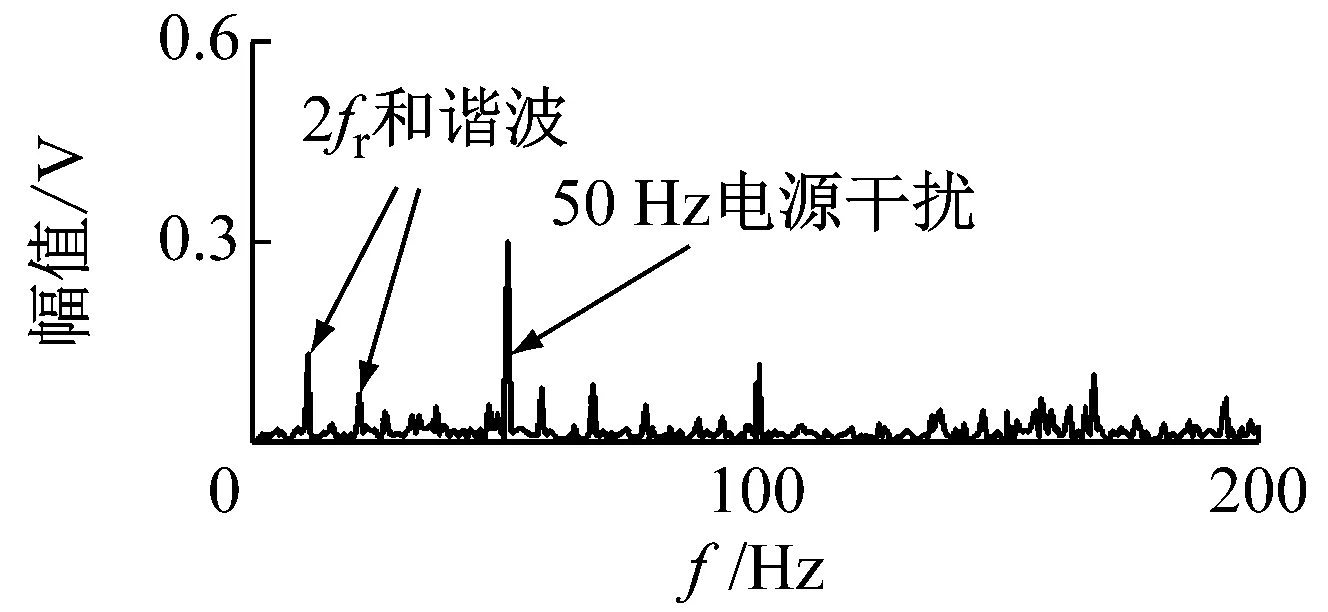
(a)[0,978 Hz]

(b)[978 Hz, 2 524 Hz]

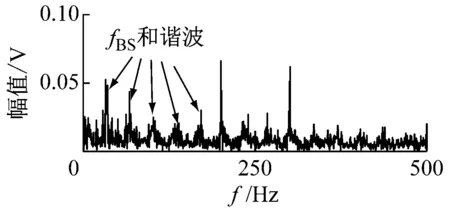
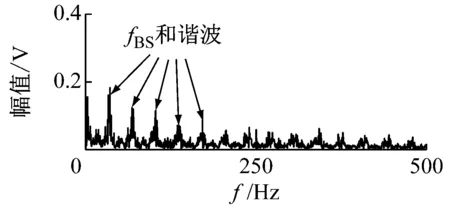
(c)[978 Hz, 5 000 Hz]图14 包络谱Fig.14 The envelope spectrum

如图14所示,在[978 Hz, 2 524 Hz]和[2 524 Hz, 5 000 Hz]区间的包络谱中的频率成分为滚子的特征频率及其谐波。但是在图14(a)中，存在很明显的电源干扰成分。这就导致转频的2倍频2fr及其谐波没有VFWEO谱中明显。为了进一步降低干扰的影响，使用VFWEO对EWT分解后的分量进行解调，其VFWEO谱，如图15所示。

如图15所示,在[978 Hz, 2 524 Hz]和[2 524 Hz, 5 000 Hz]区间的包络谱中，可以发现滚子的特征频率及其谐波。在图15(a)中，转频的2倍频2fr及其谐波更明显，说明干扰的影响进一步降低。

(a)[0,978 Hz]

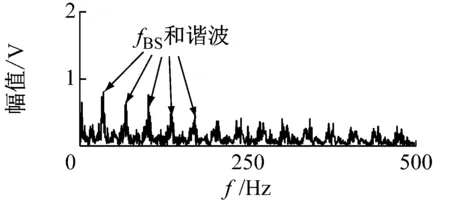
(b)[978 Hz, 2 524 Hz]

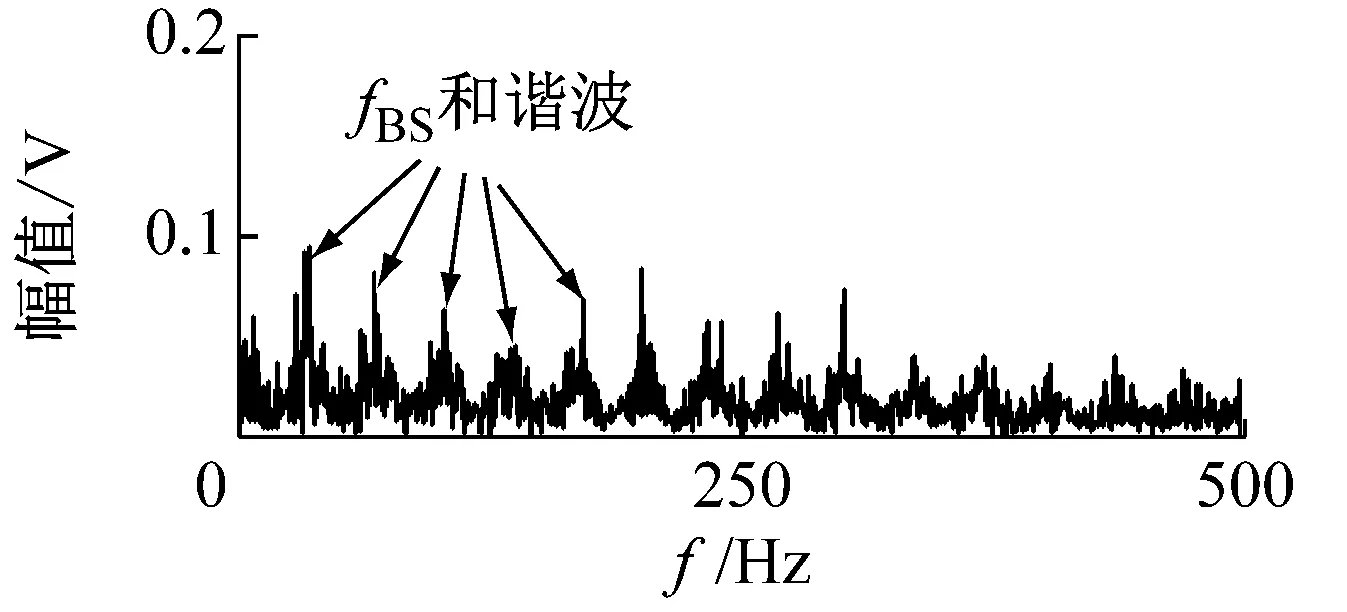
(c)[978 Hz, 5 000 Hz]图15 VFWEO谱Fig.15 The VFWEO spectrum

4 结 论

变步长频率加权能量算子通过使用变步长中点平均差分代替传统的中点平均差分，从而改善了频率加权能量算子在中心频率较低时鲁棒性差的缺点。同时，研究发现不同的步长参数可以实现针对不同的共振频带的解调。因此，变步长频率权重能量算子可以在未进行信号分解的前提下实现对不同共振频带的解调。变步长频率加权能量算子简化了信号处理的步骤，使其在工程实际领域中具有较高的应用价值。最后使用仿真信号与实测信号对该算法进行了验证。实验表明该算法可以在强噪声环境下有效的实现不同频带的解调从而提取其中的故障信息，实现早期微弱故障的诊断与报警。