冲击渐进振动系统的双参数分岔分析

吕小红, 罗冠炜

(1. 兰州交通大学 机电工程学院， 兰州 730070； 2. 甘肃省轨道交通装备系统动力学与可靠性重点实验室， 兰州 730070)

冲击振动现象大量存在于动力机械系统中，这会使得系统呈现复杂的动力学响应。因此，冲击振动系统动力学的研究是近十几年来机械和振动工程界感兴趣的一个研究方向，同时，冲击振动系统动力学的应用研究也引起了很多学者的关注。Wen等[1]研究了冲击振动系统的退化Hopf分岔。张永祥等[2]研究了冲击振动系统在余维三分岔点邻域内的动力学特性。乐源[3]推导了三自由度冲击振动系统对称周期运动的解析表达式，研究了对称不动点在余维二分岔点邻域内的局部两参数动力学行为。李群宏等[4]结合理论推导和数值模拟研究了双自由度碰振系统的单碰亚谐运动。朱喜锋等[5]研究了两自由度软冲击振动系统的颤振运动及其转迁规律。张思进等[6]推导了线性碰振系统单碰周期振动的擦边分岔方程，并以单自由度系统为例验证了解析结果的正确性。Chillingworth[7]和Humphries等[8]应用不连续几何的拓扑方法研究了碰撞振动系统在擦边分岔点附近鞍结分岔存在与否的原因。Liu等[9]研究了三自由度碰撞振动系统的光滑和非光滑分岔，揭示了系统在擦边分岔点附近的不连续跳跃和多解共存现象。冯进钤等[10-11]基于图胞映射理论研究了确定和随机两种情形下，Duffing碰撞振子擦边诱导的两种激变形式，以及鞍结分岔、混沌鞍激变分岔和混沌内部激变分岔等三类分岔的动力学。Peterka等[12-13]研究了冲击振动系统各类周期振动的存在域和稳定性问题，揭示了系统周期振动的转迁规律以及相互转迁过程中的迟滞现象。Wiercigroch等[14-15]以冲击钻和钻孔桩等带有钻进运动的机械系统为工程背景，研究了其动力学模型的分岔特点和动力学参数对钻进性能的影响。

在一定参数条件下，冲击振动系统可能呈现p/1类基本碰撞运动。国内外对此类周期振动的稳定性及分岔研究报道较少，而且已有的对冲击振动系统动力学的研究基本都是基于单参数分岔进行分析的，很难全面揭示系统丰富的动力学行为和周期振动的分岔特点。本文以小型振动冲击式打桩机为工程背景，建立了考虑缓冲垫和支撑介质黏弹性的冲击渐进振动系统的力学模型。研究系统的各类周期振动在二维参数(激振频率ω和预压量l)平面内的参数区域和分布规律，揭示p/1基本碰撞运动的分岔特点，为解决特定工程实际问题提供一定的理论依据和参考。

1 冲击渐进振动系统的动力学模型

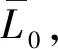
图1 力学模型Fig.1 Mechanical model

引入以下无量纲参数

(1)

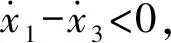
(2)

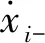
(3)

激振器M1与缓冲垫黏滞运动过程中，F1>0。待F1减小至零时，两者分离。黏滞运动结束瞬间，F1=0，x1=x3+l。黏滞运动结束后，激振器M1自由振动，缓冲垫在其自身弹性和阻尼的作用下恢复到平衡状态，随质块M2一起自由振动。

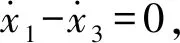
用P0表示作用于滑块的弹性恢复力和阻尼力的合力，有

(4)

当激振器M1第k次冲击缓冲垫后，两者黏滞向下运动，弹簧K3被压缩，最终使得作用于滑块的合力P0的绝对值增加。当P0满足-P0>f时，滑块克服干摩擦力f渐进运动，渐进的深度为lk，同时系统向下平移lk。当P0的绝对值减小至等于干摩擦力f时，滑块渐进运动过程结束，滑块与周围介质接触面间的摩擦力f由动摩擦力变为静摩擦力，直到滑块开始下一次渐进运动为止。不管滑块处于哪种状态，系统的静平衡位置相对滑块而言都没有改变。

2.3.2 药物因素 在对危重患者实施治疗的过程中，某些药物可导致患者出现一系列不良心理反应。如使用利多卡因治疗心律不齐，当静脉滴注速度达到4 mg/min时，大部分患者可出现谵妄等精神症状［5］。将巴比妥类，抗胆碱能药(尤其是东莨菪碱)作为术前用药，将增加麻醉苏醒期兴奋、烦躁的发生率。氯胺酮麻醉后的患者发生情感改变的概率较高，因麻醉性镇痛药引起的苏醒延长，常用纳洛酮进行拮抗，但纳洛酮同时会逆转阿片激动剂的所有作用，包括镇痛。患者会突然出现疼痛，引起明显的交感神经兴奋等［14］。

根据前面的分析，激振器M1冲击缓冲垫后，两者或黏滞运动然后分离，或立即分离，直至下次冲击发生。滑块静止或渐进运动。因此，系统在渐进振动过程中可能呈现四种不同的运动状态。下面给出每种运动状态的判断条件及运动微分方程：

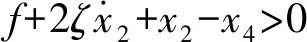
(5)

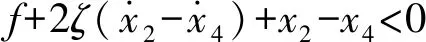
(6)

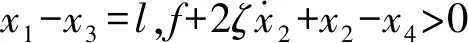
(7)

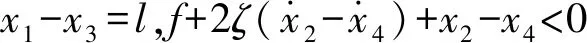
(8)

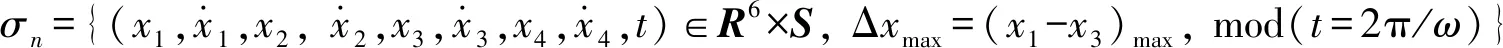
X′=f(v,X)

(9)

2 基本碰撞运动的参数域和分岔特点

选取一组参数：μm=0.35，μk=0.03，μc=0.03，μk3=0.7，μc3=0.7，ζ=0.1，f=0.5，应用前面定义的两种Poincaré映射辨识在二维参数平面(ω∈(0.04，1)，l∈(0，15))内各点处，系统呈现的周期振动的类型如图2(a)所示。在图中没有用符号p/n标注的灰色区域内，系统主要呈现概周期运动或混沌运动。在图2(a)所示二维参数区域内，系统主要呈现p/1(p=1, 2, 3)类基本碰撞运动。图2(b)为p/1基本碰撞运动的分岔线示意图。图中PD表示周期倍化分岔线，PB表示周期泡型分岔线，Gr表示实擦边分岔线，Gb表示虚擦边分岔线，SN表示鞍结分岔线，MS表示多重滑移分岔线，HP表示Hopf分岔线。图2(c)和图2(d)分别为激振器M1冲击缓冲垫的速度和滑块在一定时间内(t=200)的渐进量在(ω，l)参数平面内的分布图。图中1/1振动的响应和其余类型振动的响应分别用不同的颜色线型表示。图3(a)和图3 (b)为ω=0.5，l=0.5时，系统呈现1/1基本碰撞运动的相图和时间历程图。每个激振力周期内，激振器M1冲击缓冲垫一次，冲击后，两者黏滞向下运动。当作用于滑块的合力P0满足-P0>f时，滑块克服干摩擦力f渐进运动，且具有一定的渐进量。

2.1 1/1基本碰撞运动的分岔分析

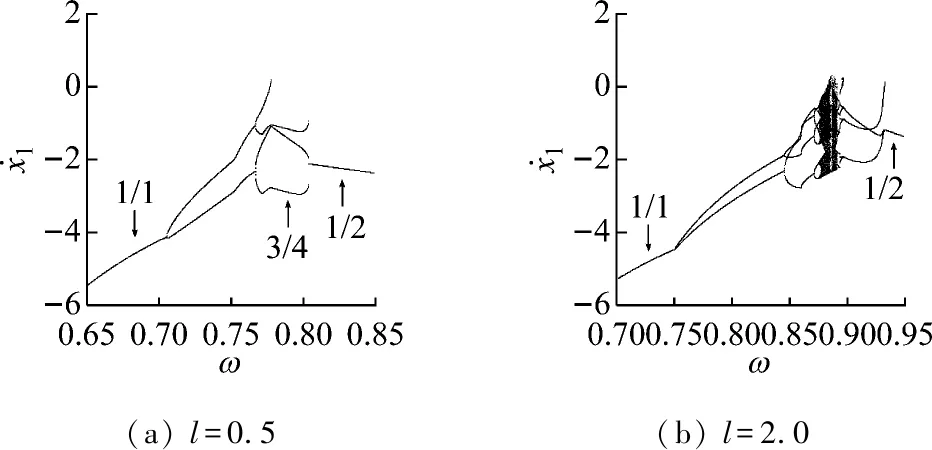
如图2(a)所示，1/1基本碰撞运动的参数域被灰色区域分割为两个子区域S1和S2。子区域S1的边界线为1/1基本碰撞运动的虚擦边分岔线(Gb)、Hopf分岔线(HP)和周期倍化分岔线(PD)。子区域S2的边界线为1/1基本碰撞运动的多重滑移分岔线(MS)和周期倍化分岔线(PD)，见图2(b)。在子区域S1和S2中，增加ω穿越周期倍化分岔线(PD)时，1/1基本碰撞运动经周期倍化分岔产生2/2周期振动。ω继续增加，1/1基本碰撞运动的分岔过程受预压量l的影响较大。当l很小时，2/2周期振动经周期倍化分岔产生4/4周期振动，ω进一步增加，系统在一个振动周期内，冲击速度最小的一次冲击逐渐消失，4/4周期振动经鞍结分岔产生3/4周期振动，见图4(a)。对于略大的l，当ω增加时，1/1基本碰撞运动经倍周期序列最终通向混沌，见图4(b)。

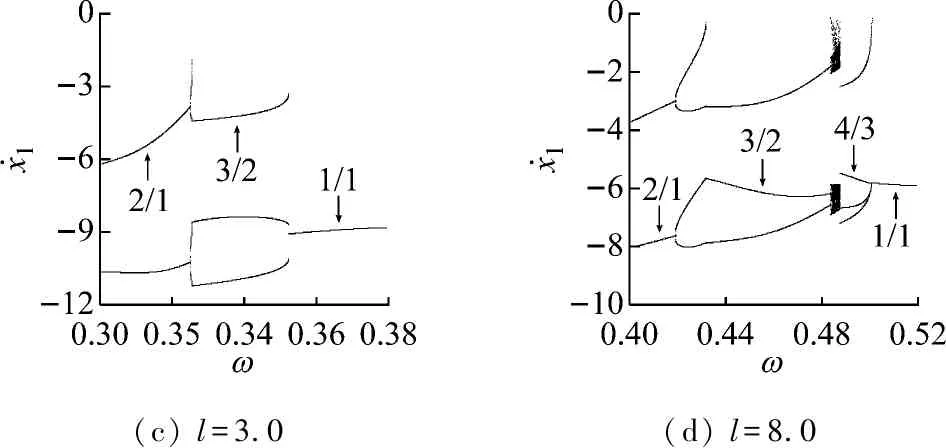
在子区域S1中，减小ω穿越擦边分岔线时，1/1基本碰撞运动发生擦边分岔，使得系统在一个振动周期内的激振力周期数和碰撞次数都发生了变化，根据文献[16]的结论，此擦边分岔线为虚擦边分岔线(Gb)。由图2(a)可见，在子区域S1和2/1基本碰撞运动的参数域之间存在一个中间过渡区域。中间过渡区域的右边界线为1/1基本碰撞运动的虚擦边分岔线(Gb)，左边界线为2/1基本碰撞运动的周期倍化分岔线(PD)。l增加，中间过渡区域对应的ω区间略有增加。中间过渡区域内，存在3/2，4/2和4/3等周期振动的参数岛。固定l，当ω变化时，中间过渡区域内存在两种转迁过程，分别对应小l区间和较大的l区间。以l=3.0和l=8.0为例，图4(c)和图4 (d)给出了两种转迁过程的单参数分岔图。图中4/2周期振动由2/1基本碰撞运动的周期倍化分岔产生，3/2周期振动和4/2周期振动之间经实擦边分岔和鞍结分岔相互转迁。由此可见，由于虚擦边分岔的发生，使得1/1基本碰撞运动在向稳定的2/1基本碰撞运动转迁的过程中出现一个中间过渡区域。中间过渡区域内的2/1基本碰撞运动都是不稳定的，系统由不稳定的2/1基本碰撞运动转迁为3/2或4/3等周期振动或混沌运动。ω继续减小，2/1基本碰撞运动逐渐由不稳定变为稳定，系统的运动退出中间过渡区域，嵌入2/1基本碰撞运动的参数域。

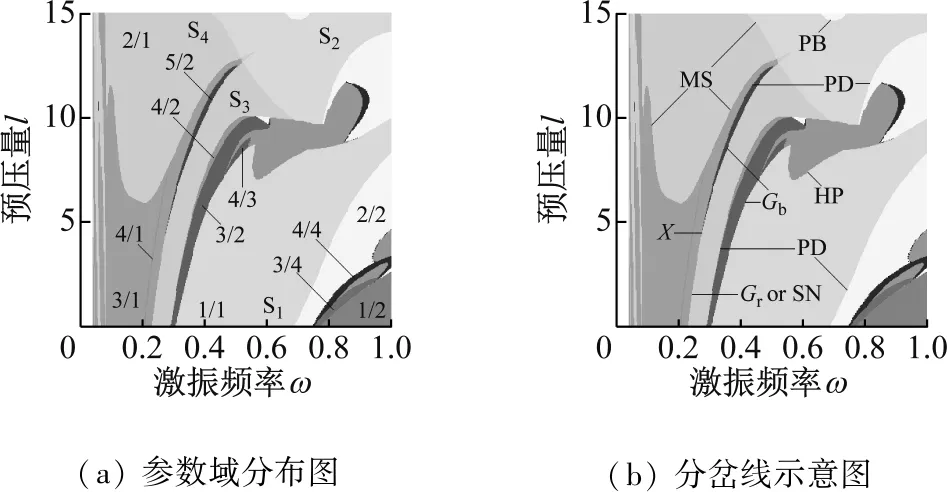
(a) 参数域分布图(b) 分岔线示意图

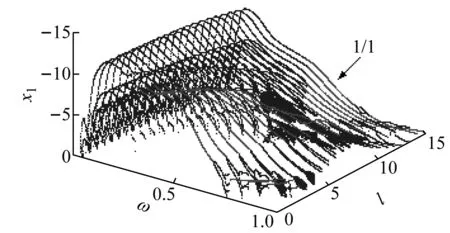
(c) 冲击速度分布图

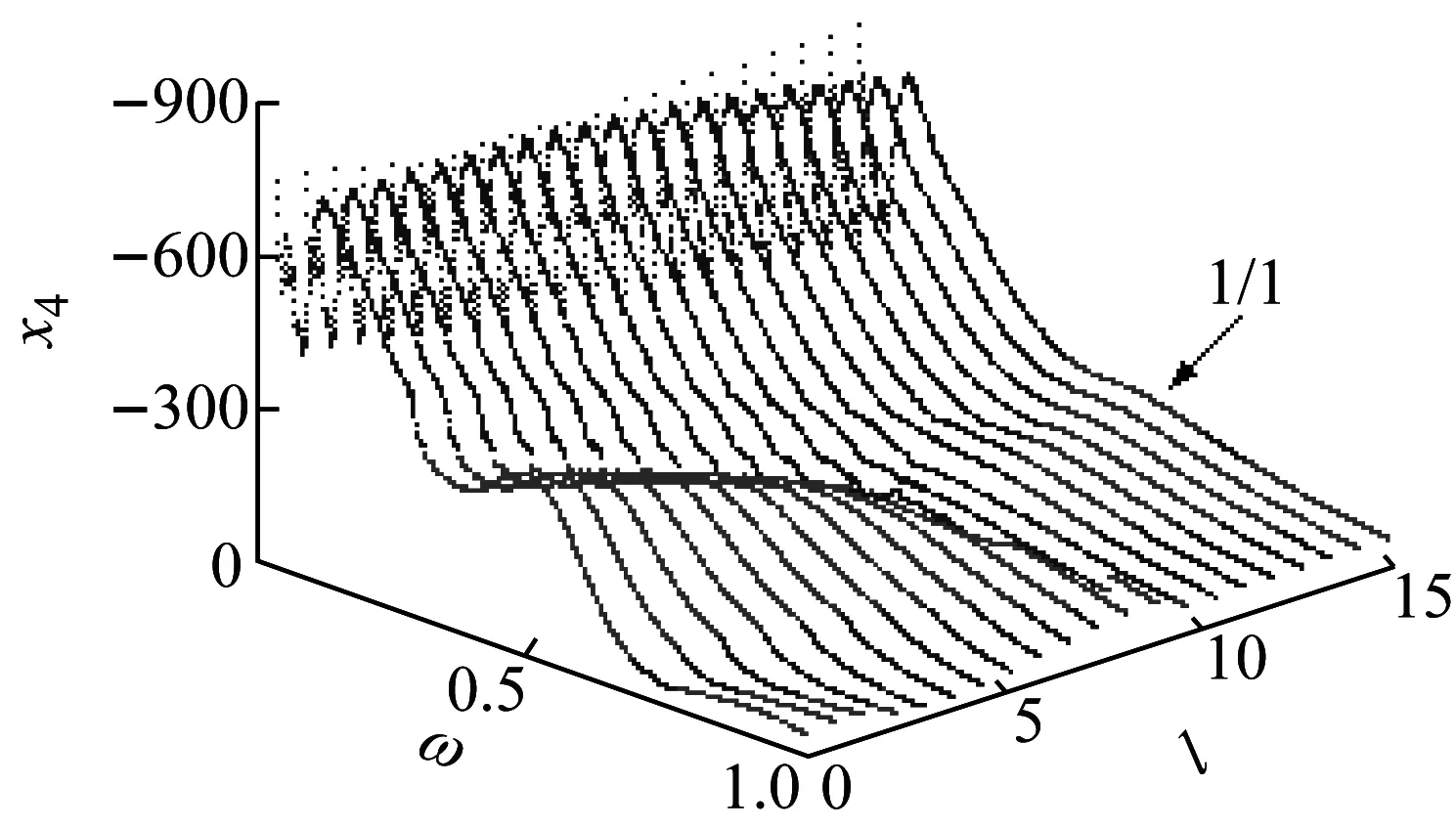
(d) 有限时间内滑块的渐进量分布图图2 二维参数平面分布图Fig.2 Distribution diagram in two-dimensional parameter plane

(a) 相图(b) 时间历程图

图3 1/1基本碰撞运动的响应图

Fig.3 Response of 1/1 fundamental impact motion

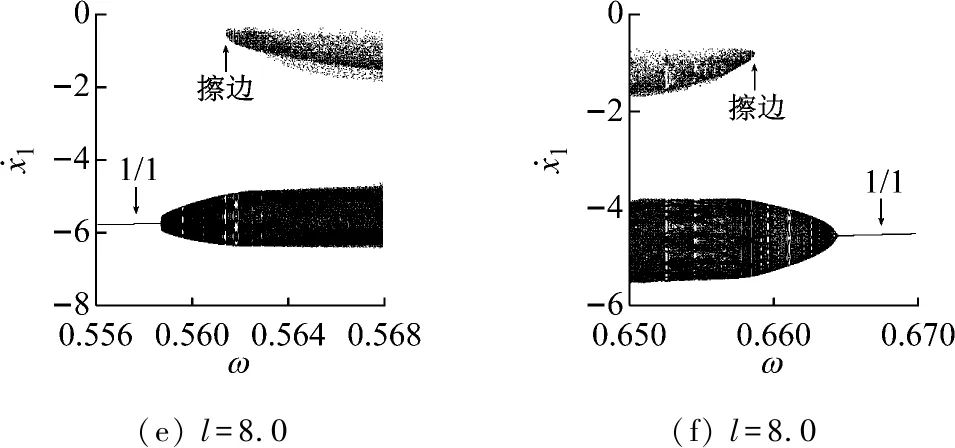
子区域S1和灰色区域之间的分界线为1/1基本碰撞运动的Hopf分岔线(HP)。以l=8.0为例，图4(e)和(f)给出了1/1基本碰撞运动随ω变化发生Hopf分岔产生概周期运动，然后经擦边概周期运动转迁为混沌的单参数分岔图。当ω= 0.558 5时，1/1基本碰撞运动发生Hopf分岔，产生概周期运动，图5(a)给出了ω=0.559时的Poincaré映射图和时间历程图。ω增加，环面逐渐扩张。在某相邻两次冲击之间，出现了激振器M1上下往复振动两次，冲击一次缓冲垫的运动过程。ω继续增加，没有冲击的一次振动的振幅逐渐增加，最终使激振器M1与缓冲垫擦碰接触，系统呈现1/1基本碰撞运动的擦边概周期运动，见图5(b)。当ω=0.562时，取Hopf分岔前1/1基本碰撞运动的不动点为初始映射点，当映射至第556次时，激振器M1以很小的速度冲击缓冲垫。第555次和第557次冲击的时间间隔大约为一个激振力周期，即在1/1运动的概周期运动模式中夹杂有近似2/1运动，导致系统的相位角发生突变，环面震荡，Poincaré映射图出现两块区域，概周期运动经擦边分岔转迁为混沌，见图5 (c)。

(a) l=0.5(b) l=2.0

(c) l=3.0(d) l=8.0

(e) l=8.0(f) l=8.0

图4 1/1基本碰撞运动的分岔图

Fig.4 Bifurcation diagrams of 1/1 fundamental impact motion

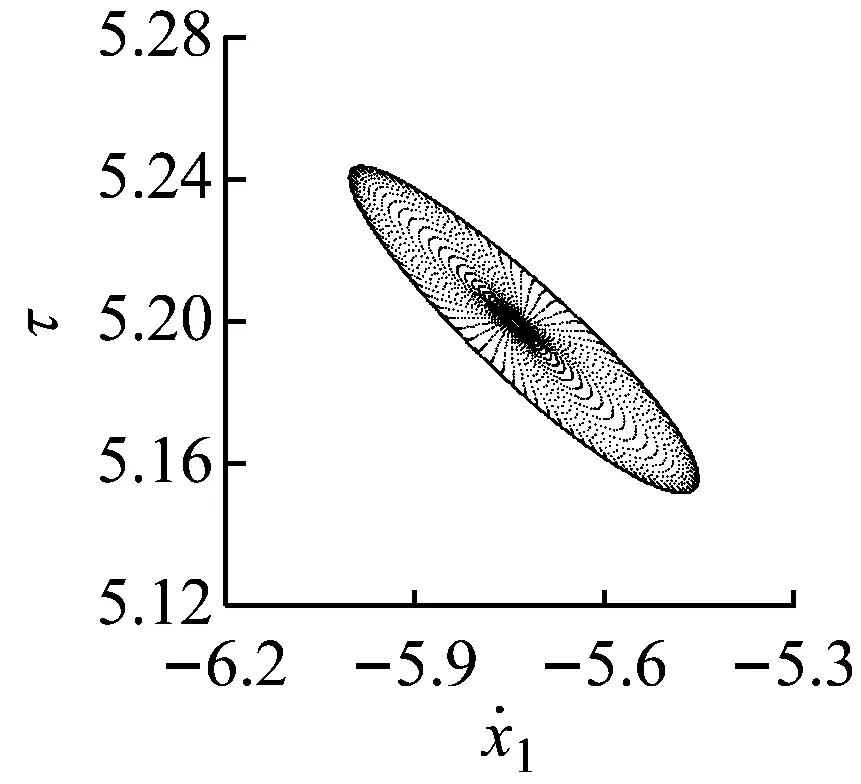
(a) 概周期运动，ω=0.559

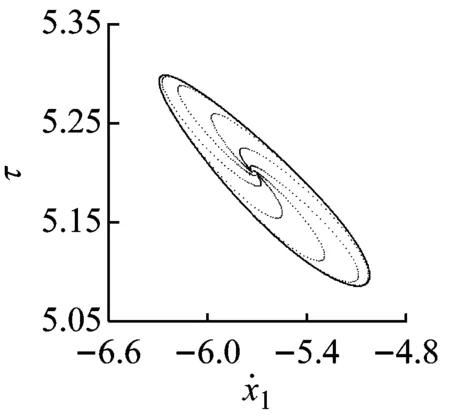
(b) 擦边概周期运动，ω=0.561 5

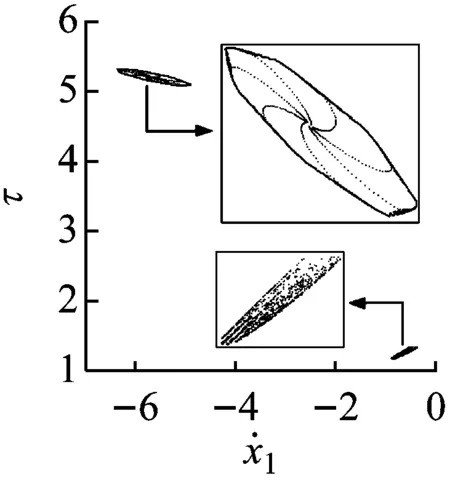
(c) 混沌，ω=0.562图5 Poincaré映射图和时间历程图，l=8.0Fig.5 Poincaré maps and time series, l=8.0

子区域S2的左边界线为1/1基本碰撞运动的多重滑移分岔线(Multi-Sliding Bifurcation)(MS)。以l=12.0为例进行分析，图6(a)为ω=0.6，系统呈现1/1基本碰撞运动时，激振器M1和缓冲垫的相对位移时间历程图。一个激振力周期内，激振器M1冲击一次缓冲垫。冲击后，两者黏滞运动，见图6(a)中的水平直线。当ω减小至大约0.55附近时，黏滞期内出现了激振器M1与缓冲垫短暂分离的现象，即所谓的隆起现象，见图6(b)，使得系统在一个激振力周期内的碰撞次数和黏滞次数各增加一次，呈现2/1基本碰撞运动。Wagg[17]研究了两自由度振动系统在黏滞期内的隆起现象，由此产生的分岔称为隆起分岔(Rising bifurcation)，然后证明了隆起分岔在性质上与摩擦振动系统和继电反馈系统中的多重滑移分岔相似。因此，子区域S2的左边界线为1/1基本碰撞运动的多重滑移分岔线。

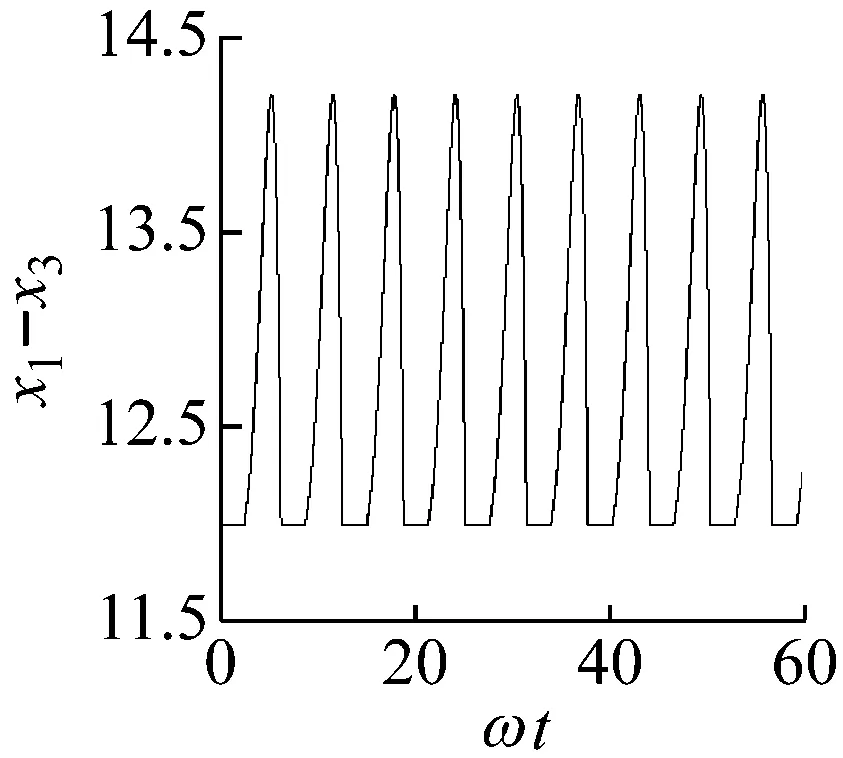
(a) 1/1基本碰撞运动，ω=0.6

(b) 2/1基本碰撞运动，ω=0.55图6 相对运动的时间历程图，l=12.0Fig.6 Time series of relative motion, l=12.0

在子区域S2中嵌有一个2/2周期振动的小面积的参数岛，其与子区域S2之间的分界线为1/1基本碰撞运动的周期泡型分岔线(PB)，见图2(a)和图2(b)。当ω增加或减小时，系统的分岔过程为：1/1基本碰撞运动→周期倍化分岔→2/2周期振动→逆周期倍化分岔→1/1基本碰撞运动。图7给出了l=15.0时，系统发生周期泡型分岔的单参数分岔图。

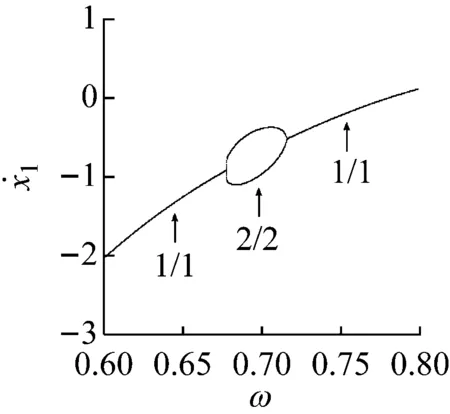
图7 周期泡型分岔，l=15.0Fig.7 Type of periodic bubble bifurcation, l=15.0

2.2 2/1基本碰撞运动的分岔分析

由图2(a)可见，2/1基本碰撞运动的参数域也被分割为两个子区域S3和S4。由前面的分析可知，子区域S3的上边界线为1/1基本碰撞运动的多重滑移分岔线(MS)，右边界线为2/1基本碰撞运动的周期倍化分岔线(PD)，见图2(b)。在子区域S3的左边界线上存在一个奇异点X。奇异点X是2/1基本碰撞运动的实擦边分岔线(Gr)和虚擦边分岔线(Gb)以及3/1基本碰撞运动的鞍结分岔线(SN)和周期倍化分岔线(PD)的交点。在llx的区域内，子区域S3的左边界线为2/1基本碰撞运动的虚擦边分岔线(Gb)。由于虚擦边分岔的发生，使得2/1基本碰撞运动在向稳定的3/1基本碰撞运动转迁的过程中出现一个中间过渡区域，见图2(a)。中间过渡区域被2/1基本碰撞运动的虚擦边分岔线(Gb)和3/1基本碰撞运动的周期倍化分岔线(PD)包围。中间过渡区域内，存在5/2和6/2周期振动的参数岛。其中，6/2周期振动由3/1基本碰撞运动的周期倍化分岔产生，5/2周期振动和6/2周期振动之间经实擦边分岔和鞍结分岔相互转迁。以l=12.0为例，图8(b)给出了ω穿越中间过渡区域时的单参数分岔图。

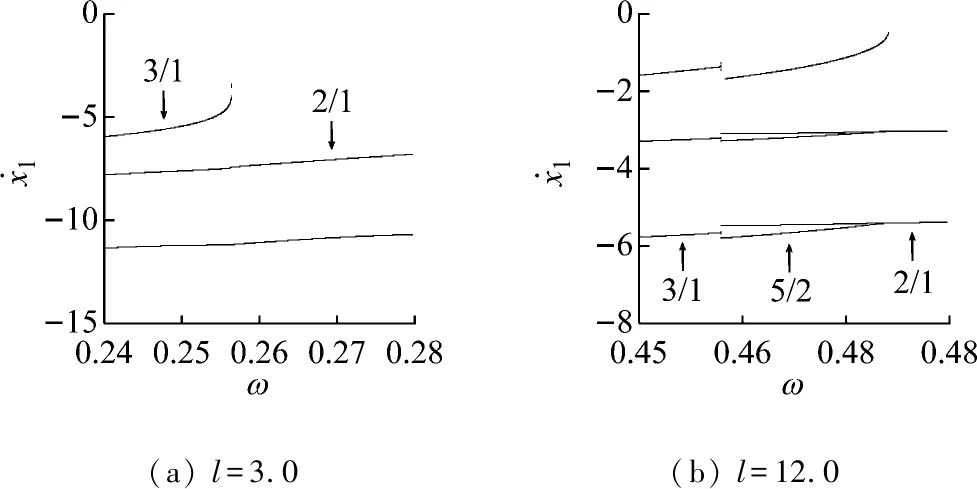
(a) l=3.0(b) l=12.0

图8 2/1基本碰撞运动的分岔图

Fig.8 Bifurcation diagrams of 2/1 fundamental impact motion

子区域S4和3/1基本碰撞运动的参数域之间的分界线为2/1基本碰撞运动的多重滑移分岔线(MS)。以l=12.0为例进行分析，图9(a)为ω=0.43，系统呈现2/1基本碰撞运动时，激振器M1和缓冲垫的相对位移时间历程图。一个激振力周期内，激振器M1冲击两次缓冲垫。每次冲击后，两者黏滞运动，见图9(a)中的水平直线。其中第二次冲击后的黏滞运动时间比第一次冲击后的黏滞运动时间较长。当ω增加至大约0.45附近时，第二次黏滞期内出现了激振器M1与缓冲垫短暂分离的现象，2/1基本碰撞运动发生多重滑移分岔，使得系统在一个激振力周期内的碰撞次数和黏滞次数各增加一次，呈现3/1基本碰撞运动，见图9(b)。

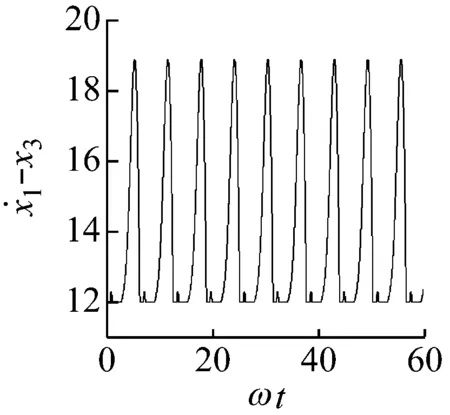
(a) 2/1基本碰撞运动，ω=0.43

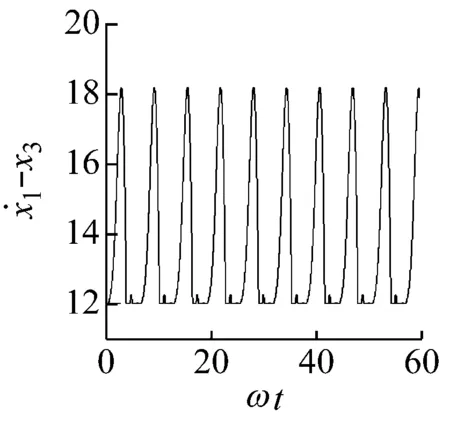
(b) 3/1基本碰撞运动，ω=0.45图9 相对运动的时间历程图，l=12.0Fig.9 Time series of relative motion, l=12.0

3 基本碰撞运动的冲击速度和滑块渐进量

为了更全面、更深入的认识图1所示系统的动力学性能，需要研究系统参数、冲击速度和滑块渐进率之间的关联关系。由图2(a)，图2 (c)和图2 (d)可见，激振器M1冲击缓冲垫的速度越大，滑块的渐进率越好。对于p/1基本碰撞运动而言，p越大，其冲击速度的峰值以及滑块在有限时间内的渐进量的峰值越大。但是，p越大，意味着在一个激振力周期内，激振器M1冲击缓冲垫的次数越多，引起不利的后果越明显。因此，综合考虑各方面因素，实际工程应用应优先选择1/1基本碰撞运动的最大渐进量。在1/1基本碰撞运动的子区域S1中，l增大，存在1/1基本碰撞运动的ω区间增加，但是冲击速度的峰值和滑块在有限时间内(t=300)的最大渐进量却减小。选择合适的预压量，并确定动力学参数的合理匹配规律，有利于使系统在较宽的激振频率区间呈现稳定的1/1基本碰撞运动，并获得较大的瞬时冲击速度和较好的渐进效果。

4 结 论

本文建立了考虑缓冲垫和支撑介质黏弹性并能够模拟有界渐进运动的冲击渐进振动系统的力学模型。通过二维参数分岔分析得到在二维参数平面(ω∈(0.04，1)，l∈(0，15))内各点处，系统呈现的周期振动的类型，揭示了1/1和2/1基本碰撞运动的分岔特点，以及系统参数、冲击速度和滑块渐进率之间的关联关系。

(1)ω增加，1/1基本碰撞运动通常发生周期倍化分岔产生2/2周期振动。ω减小时，1/1基本碰撞运动的分岔特点跟预压量l有关。在小l区域内，减小ω，1/1基本碰撞运动经虚擦边分岔产生不稳定的2/1基本碰撞运动。在大l区域内，减小ω，1/1基本碰撞运动经多重滑移分岔产生2/1基本碰撞运动。此外，在一定的参数条件下，系统呈现1/1基本碰撞运动的概周期运动和周期泡现象。

(2)ω变化时，2/1基本碰撞运动经实擦边分岔，虚擦边分岔或多重滑移分岔产生3/1基本碰撞运动。由于p/1(p=1, 2)基本碰撞运动的虚擦边分岔，使得p/1基本碰撞运动在向稳定的(p+1)/1基本碰撞运动转迁的过程中出现一个中间过渡区域。中间过渡区域内，存在(2p+2)/2，(2p+1)/2和(3p+1)/3等周期振动的参数岛。

(3) 激振器M1冲击缓冲垫的速度越大，滑块的渐进率越好。对于p/1基本碰撞运动而言，p越大，其冲击速度的峰值以及滑块在有限时间内的渐进量的峰值越大，但引起不利的后果越明显。因此，实际工程应用的最佳选择应该是使系统工作于1/1基本碰撞运动的冲击速度峰值附近。