基于索引冗余字典的轴承故障组稀疏分类方法研究
2019-04-22林建辉黄晨光
邓 韬, 林建辉, 黄晨光, 靳 行
(1. 西南民族大学 电气信息工程学院, 成都 610041; 2. 西南交通大学 牵引动力国家重点实验室,成都 610031)
高速列车轮对轴承故障检测的重点在于其早期故障预警。声发射检测作为一种故障早期检测手段其信号比振动加速度频率范围宽、包含的信息量大,能捕捉轴承微小的故障信号。轴承内部运动状态复杂,滚动体与保持架、内外圈、挡边之间呈现高度复杂的运动关系,故障信号易出现双冲击混叠等,加上其他噪声干扰给声发射信号特征提取及其故障诊断带来一定困难[1]。轮轴故障的诊断实际上就是对故障信号进行模式分类,提高分类器的工程实用性是高性能分类器研究的重要目标之一。
目前对高速列车轴承故障的多级、多态分辨仍存在困难。如采用人工神经网络易陷入局部极小值,其结构类型依赖于经验[2]。SVM方法在多分类时难以保证内部所有的二分类器核参数及惩罚因子选取的最优性。近年采用稀疏表示的分类方法(Sparse Representation-based Classification, SRC)在图像、语音分类上表现优异,无需多个二分类器组合[3],仅通过样本在字典下稀疏解的重构,就可实现理想的多分类效果。研究轴承故障声发射信号的SRC分类,对高速列车运营安全有积极意义。
文献[4]揭示了SRC优异性能更多是基于样本间协作而非稀疏性, 并以L2范数替换L1范数设计了协作表示分类器(Collaborative Representation Classifer, CRC)提升分类速度,但未考虑样本类标签。Majumdar等[5]提出采用L1L2混合范数求解的组稀疏分解模型(Group SRC),可减小稀疏系数分散,实现最佳相关原子选取。此外,基于核协作表示分类器[6]和加权的组稀疏算法[7](Weighted GSR)也相继出现,前者通过核空间取代字典原子和信号的内积运算来解决范数归一化问题,对非线性成分更敏感,但分类效果和优化机制还有待验证。后者通过距离加权做约束,但复杂信号匹配差,且距离约束方法与组范数特性相违背。
本文针对轴承故障的组稀疏分类,设计了一种带索引的故障冗余字典,利用信号多尺度排列熵为原子构成索引字典,实现快速预匹配以缩小故障类范围,加快收敛速度。通过在组LASSO算法中结合邻近梯度与最优一阶优化来减小计算量;在字典原子获取上,利用改进EEMD结合VMD方法对轮对信号作分解,实现原子自适应获取,以保留故障非线性特征。同时设计了一种原子区间平移稀疏编码方法来提高原子匹配性。
1 组稀疏分类
1.1 GSRC原理
定义一个超完备字典D=[d1,d2,…,dK],D∈Rm×n,D中内部原子数为n,m代表每个原子的长度,di代表每个类别原子集合。设X∈Rm是待稀疏分类的目标信号,则基于字典D对X进行稀疏逼近可通过下式表述
(1)
式中:C为稀疏分解系数向量,稀疏分类的前提是基于足够多的原子,目标信号能用其所属类别中原子的某种线性组合进行表述。当一个超完备字典包含数个不同类别原子时,目标信号稀疏表示的非零值将主要对应其所属类别原子,稀疏逼近误差为
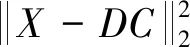
(2)
寻找稀疏重构误差最小的那类就可判断目标信号的分类,即
identity(X)=argmin(εi)
(3)
要获得最终分类结果,实际上是解决凸优化问题。
1.2 组LASSO方法
凸优化求解主要有基追踪(BP)、匹配追踪(MP)、正交匹配追踪(OMP)和基于迭代回归的凸松弛算法(LASSO)等[8]。以L0范数求解最优稀疏模型是个NP难问题,LASSO算法最初由Tibshirani等对特征系数通过L1范数约束来计算,通过对稀疏系数绝对值惩罚,使绝对值之和小于某常数而不相关原子系数接近零来求解。但字典内部特征之间存在的组效应使L1范数求解存在稀疏系数分散问题,于是考虑采用L2范数的组LASSO进行GSRC求解。对一个组分类问题,设字典D共有K类n个样本构成,则第i类样本矩阵为
Di=[di,1,di,2,…,di,ni]∈Rm×ni
(4)
所有类别构成的组稀疏向量为
C=[0,…,0,ci,1,ci,2,…,ci,ni,0,…,0]T∈Rn
(5)
给定一种分类信号,不失一般,仅有若干特征对这一信号具有区别性,即从中所提取的特征对某一特定信号而言是冗余的。式(5)中除与第i类样本对应的系数外其余系数均为0或逼近0,体现出了同类样本的集中性和其他类样本的稀疏性。基于L1L2混合范数约束的GSRC模型可表述为
(6)
该模型可减小在多相关类中零散选择样本的情况,强化在同一相关类中原子选择的集中性,同时实现各组内原子的最优选择。
1.3 组LASSO求解
LASSO优化求解常采用最小角回归、快速乘法交替方向、块稀疏匹配追踪和梯度下降法。梯度下降法在计算复杂度上有一定优势,是利用迭代公式和局部梯度信息计算的一种一阶方法,即
(7)
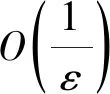
(8)
梯度步长求解邻近运算有
(9)
通过邻近梯度法获得ck展开的目标函数为
(10)
式中:ρ∈[0,1]为正则化参数,以平衡过拟合与稀疏性,搜索点bi为bi=ci+ωi(ci-ci-1)其中ωi为调节系数。对式(10)采用最优一阶加速算法有
(11)
通过设定软阈值即可求解,可明显减小计算量。
2 自适应原子故障类字典
2.1 自适应原子提取
字典可分为参数化的分析字典和基于训练的学习字典。前者通过参数波形函数获取原子,如Fourier字典、Gabor字典和基于小波时间尺度字典等,其理论成熟构造简单,但适应性和稀疏性差。学习型字典通过学习和训练获得与目标信号在结构和形态上更匹配的原子库,如采用K-SVD方法对字典原子逐列更新,但配性能仍依赖初始原子。
经验模态分解(EMD)无需基函数就可实现信号的自适应拆分,前期在文献[9]中提出了一种轴承故障声发射信号提取的改进噪声加入EEMD方法,分解效果较好。若把包含声发射特征频段的几个高频模态作为字典初始原子,将获得稀疏性很高且原子都为自适应获取的字典。但从原子体积和复杂度上看该分解并不充分,IMF内部复杂构成和噪声干扰将弱化其匹配性,因此有必要对IMF作进一步拆分。
VMD作为一种新的信号拆分新手段,通过不同频率中心及带宽迭代搜寻变分模型自适应对信号进行分离,本质是寻找所设定的K个固有模态函数估计带宽之和达到最小。考虑约束变分问题

(12)
式中:{uk}是模态集合,{wk}是其中心频率集合,σ(t)为脉冲函数;对uk分别作Hilbert变换并与指数函数e-jwkt相乘可估算uk中心频率wk。计算wk在基频带调制信号梯度L2范数,可估计uk带宽。引入一个扩展Lagrange函数
(13)
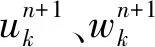
(14)

(15)

(16)
式中:τ为步长,若满足收敛条件c则停止更新,即
(17)
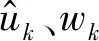
VMD方法虽然是自适应进行的,但结果受分量个数K和惩罚参数α影响。根据经验,α可参考信号采样率进行设置,不应偏离太多。K过小会出现欠分解,过大则易出现虚假模态。虚假模态与相邻模态中心频率相隔很近,因此考虑以各模态分量中心频率的最小间距限定K取值上限来避免过分解,即设定较大初始K值逐次递减做计算,直至中心频率间隔满足要求。
利用EMD分解剔除低频干扰后对剩余IMF做VMD分解易提取出较低能量的高频信息,且IMF相对窄的带宽可降低K值。把分解出的若干窄带模态作为字典原子,原子复杂性显著降低,因整个过程是自适应的,所以仍可保障匹配稀疏性。
2.2 原子区间平移稀疏编码
轴承故障一般呈现周期性,从训练数据和待分类数据中截断提取样本难以确保故障冲击波形总是位于截断数据的正中心,这种故障信号在时间轴上偏移造成的匹配误差会影响稀疏分解效果。
Smith等提出的移不变稀疏编码方法(Shift Invariant Sparse Coding, SISC),把同一模式沿时间轴平移当做独立事件,利用基函数的移不变性,即字典中原子与稀疏系数通过卷积运算实现信号逼近,每一近似波形都通过同一原子的任意时移来表达。SISC对周期信号的匹配性更强,但求解稀疏基计算量较大。对此有学者提出如差分求导或转化为频域求和来简化计算[10]。受SISC算法启发,为进一步简化计算,提出一种原子区间平移稀疏编码方法(Interval Translation Sparse Coding,ITSC)。定义平移系数∂,平移后原子为di∂。图1给出了平移操作计算步骤示意,具体步骤如下:
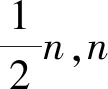
(2) 确定平移方向后,平移范围变为(-0,+a),平移中点变为+b,继续按步骤1中内积做判断。
(3) 依次做平移计算,直至迭代后新原子与信号内积无明显增加时停止,此时获得最终平移系数∂。
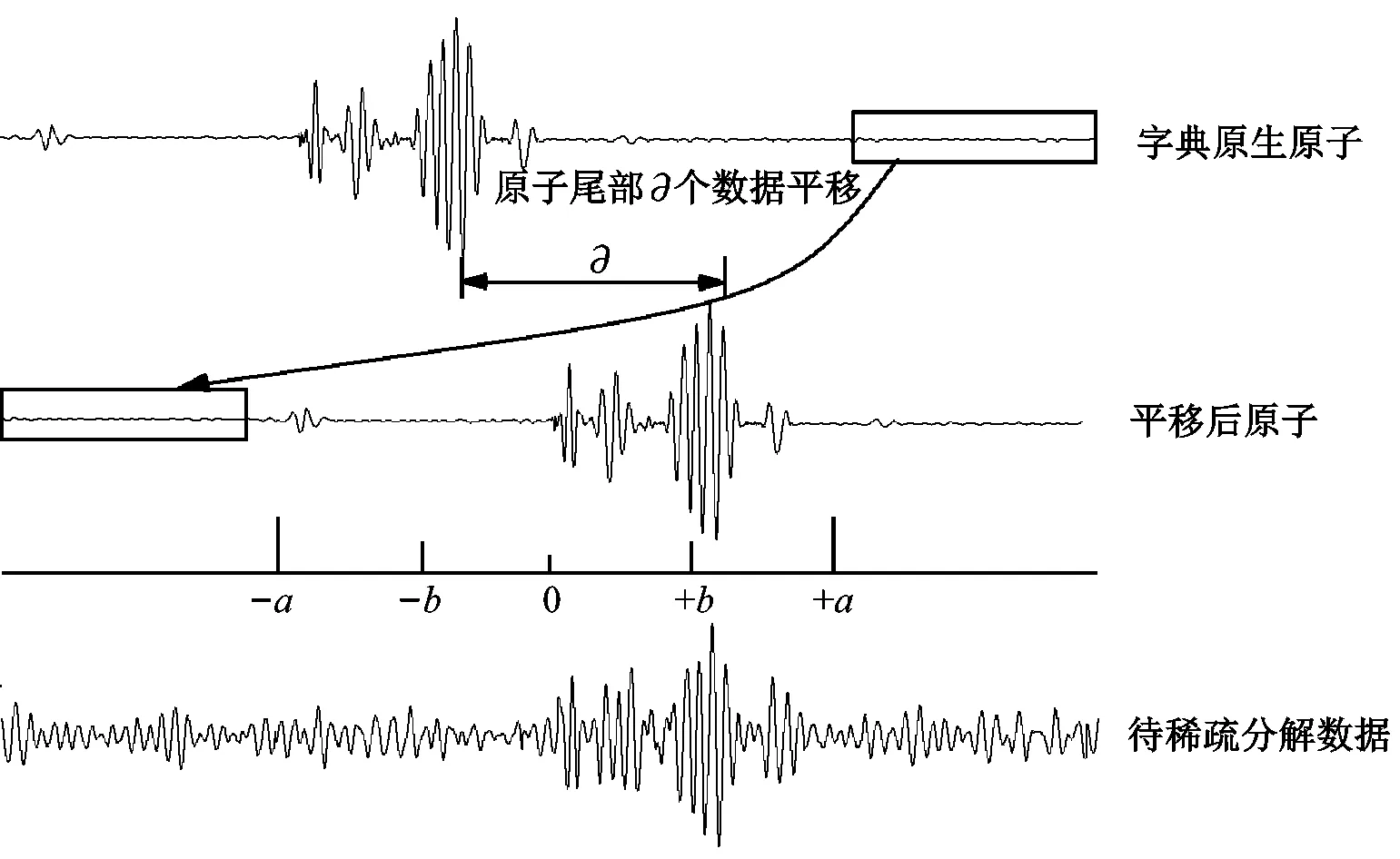
图1 区间平移构建新原子Fig.1 New atom from ITSC
即使原子特征波形与待分解信号偏移量大于原子长度一半,只需适当放宽a值大小,做一次迭代就可大幅修正偏移。为简化计算,迭代平移次数可根据原子长度设定为一恒定值。该方法针对旋转件故障信号放宽了在数据段截取上的要求,实质上是一种简便快速的基函数平移稀疏求解方法。
3 索引组合冗余字典
3.1 索引字典与索引原子
字典体积过大会导致多组类分类计算量很大。若能以长度很短的样本信号某一“特征”作为原子构成故障字典的“索引”,经过“索引”预先提取“最相关类”组成新字典再进行故障匹配,则无需字典中所有类别都参与计算。只要这一特征能较好区别各故障,与待分类信号匹配的原子所属“类”将只占整个字典类的很小部分,从而加快分类速度。
索引字典原子长度越小,其匹配时间越短。当待分类信号特征索引与索引字典原子逐一匹配后,满足不大于给定误差εsy的索引原子所指向的故障字典类被选中,εsy足够小时,选中的相关类字典组体积将远小于整个故障字典组。
构建索引字典的核心是寻找适合的字典原子。排列熵(Permutation Entropy,PE)作为一种序列随机性和动力学突变的检测方法指标,能有效反应信号内部特征,相比条件熵和样本熵其抗噪能力更强。但单一尺度排列熵还难以揭示复杂信号内部丰富信息。多尺度排列熵(Multiscal PE)能在多尺度下反应信号复杂性,噪声鲁棒性更好,在各尺度下都只输出一个无量纲参数,数据很短,故本文尝试将其作为故障声发射信号特征来构建索引字典。
考虑一个故障序列{X(i):i=1,2,…,L},首先对X作粗粒化处理,然后计算各尺度下排列熵。粗粒化序列可表示为{Y^ε(I):I=1,2,…,L/ε},其中
(18)
对Yε(I)进行相空间重构,嵌入维数为m,延迟时间为t,有
(19)
式中:每行表示一个重构分量,重构个数为k,k=L-(m-1)t,j=1,2,…,k。将尺度I下Yε的m个数据按升序重新排列,可获得如下符号序列
Sl=(j1,j2,…,jm)
(20)

(21)
Pl为1/m!时有最大值ln(m!),归一化排列熵为
(22)
排列熵中有3个重要参数,嵌入维数m、数据长度L和时延t。一般建议嵌入维数取3~7,m过小,重构序列会因包含状态太少而失去意义;m过大,会使相空间重构序列均匀化,运算量增大的同时降低对细微变化的敏感性。L,m和t之间应该根据信号实际采样率决定,L和m的取值应尽量保持正相关,t对数据序列的影响很小[11],一般取固定值1。
3.2 索引组合冗余字典
图2给出了基于索引组合冗余字典的GSRC轮对轴承故障状态分类流程。

图2 索引组合冗余字典GSRC分类流程Fig.2 The classification process of GSRC
故障样本经改进EEMD分解后选取包含典型声发射频段的IMF分量做VMD分解。以含特征频带主能量的分量重构并计算各尺度排列熵作为索引字典原子,所有分量直接作为对应故障类初始原子。重构信号多尺度排列熵受不相关频段影响小,而以全部分量作为故障类原子是为了方便信号重构。
待分类信号经同样方法分解,其多尺排列熵与索引字典原子匹配后,选中满足给定误差范围的索引原子对应类别构成新的相关类字典。为强化字典性能,故障类字典中原子可采用K-SVD优化。以最优一阶加速组LASSO算法结合ITSC对待分类模态重构信号做组稀疏匹配即可获得分类结果。
索引字典采用逐一匹配方式,各类间差异较大时,误差εsy应适当放宽来防止类别漏选。差异较小且各类间排列熵分布较一致时,εsy需尽量小,以确保选中相关类字典紧凑性,减小不相关类选中概率。
4 故障分类验证
4.1 轮轴故障设置
采用轮对跑合台获取列车轮对轴承故障声发射信号,如图3所示。WSa型声发射传感器固定于轴箱侧方呈上下放置,采样率1 Msps,放大倍率20 dB,试验速度0~200 km/h。详细制作故障设置,见表1。



图3 试验验证Fig.3 Experimental platform表1 七种故障轴承设置Tab.1 Fault setting
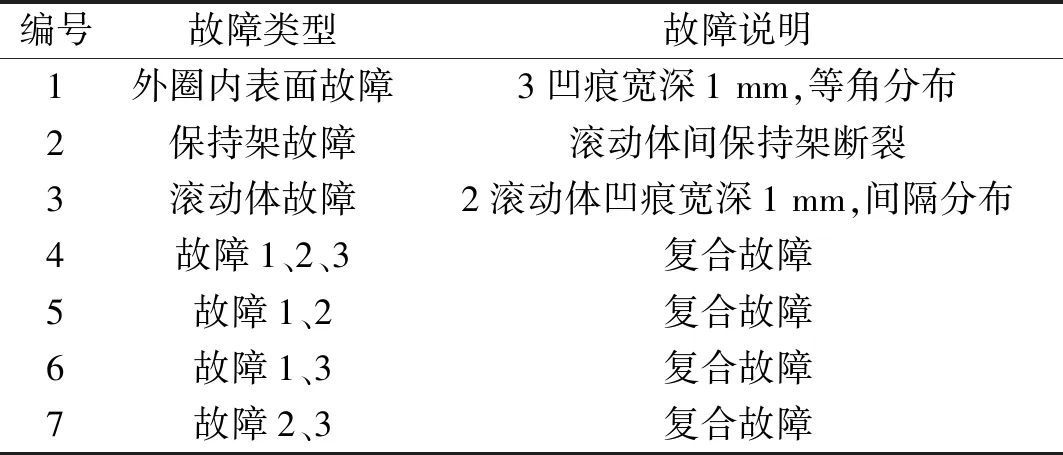
编号故障类型故障说明1外圈内表面故障3凹痕宽深1 mm,等角分布2保持架故障滚动体间保持架断裂3滚动体故障2滚动体凹痕宽深1 mm,间隔分布4故障1、2、3复合故障5故障1、2复合故障6故障1、3复合故障7故障2、3复合故障
4.2 字典原子获取
声发射数据段以包络线峭度变化结合等时间隔抽取获得。图4为200 km/h下单故障和三类复合故障声发射波形,除缺陷冲击波形外还伴有许多其他干扰,表明轴承内各部件运动声发射信号的复杂性。


图4 200 km/h速度级下故障时域图Fig.4 The 200 km/h test signals
图5为一段滚动体声发射信号经改进EEMD分解的IMF2波形图,中心频率309 kHz,频率范围272~353 kHz。对其做VMD分解,按中心频率平均间隔8 kHz设定起始分量数K=10,在290 kHz、310 kHz、330 kHz和340 kHz存在相近中心频率,见图6(a)。K值依次递减到6,中心频率见图6(b),此时相近频率模态消失。图7为分解得到的6个模态,判断前三个分量含特征频带主能量,据此重构计算多尺度排列熵获取索引字典原子,所有6个分量直接作为滚动体裂纹故障类中初始原子。

图5 滚动体裂纹改进EEMD分解后IMF2波形Fig.5 The IMF2 of a Rolling body crack signals use MEEMD

(a)
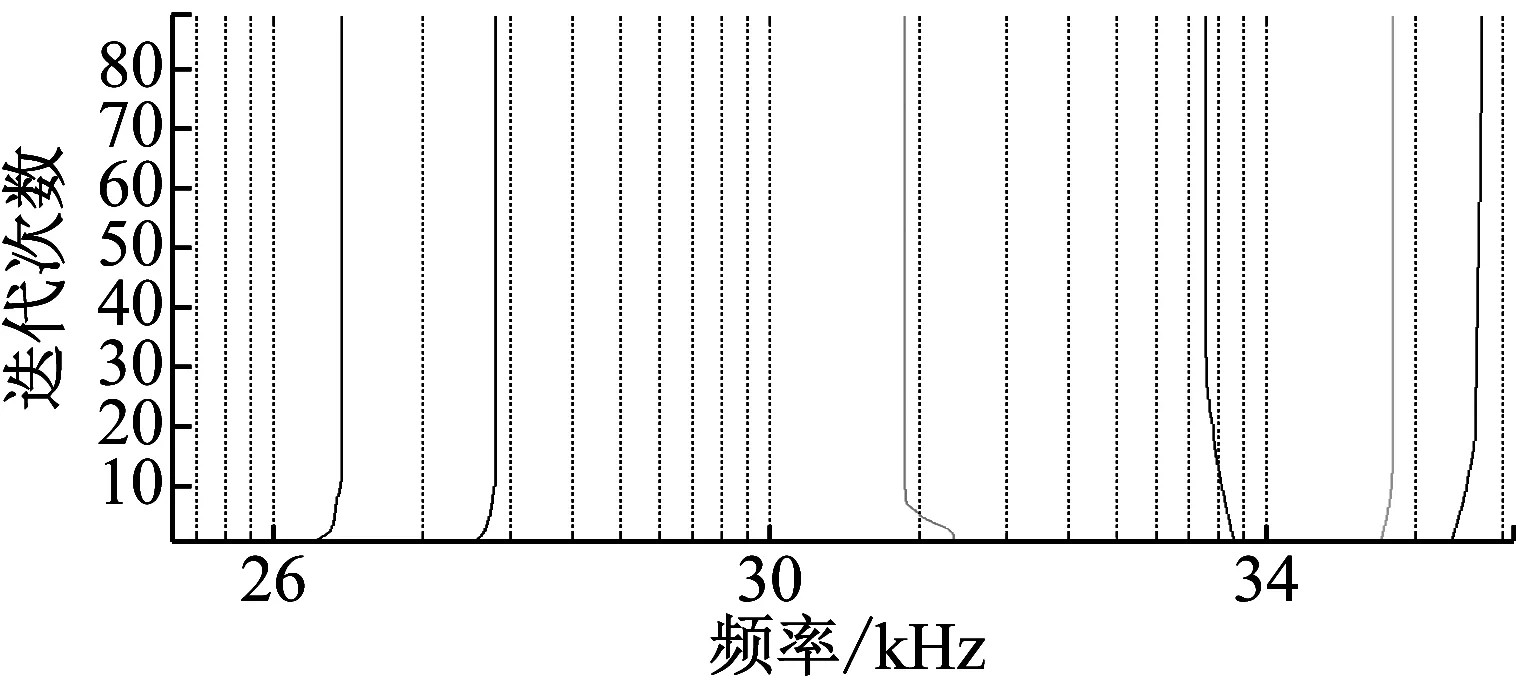
(b)图6 K取10和6时各模态中心频率Fig.6 The modal center frequency(K=10,K=6)

图7 K=6时初始原子Fig.7 The initial atoms(K=6)
分别对七类故障数据做改进EEMD分解,为减小误差,同类故障字典训练样本取自相同速度级。对100~400 kHz包含典型声发射频段的前四个IMF经VMD分解和特征频段重构,排列熵值基本在嵌入维数为6和7时进入相对稳态,在嵌入维数取7、时延t=1时计算前12个尺度下排列熵如图8所示。第2和第3个重构IMF多尺度排列熵变化曲线差异最明显,选取2、3分量的多尺度排列熵作为索引原子可获得最好的索引性能。
图9(a)和9(b)分别为随机抽取的10组单一滚动体故障和12组包含三类复合故障的多尺度排列熵。单一故下分布一致性好,表明多尺度排列熵作为索引字典原子是可行的,其他单一故障也有类似分布,限于篇幅此处未给出。复合故障存在几个不同的排列熵分布,说明信号内个组分变化多,字典训练需要更多的样本来涵盖可能出现的各类故障。排列熵计算中,冲击信号较弱时应缩短计算数据长度,否则AE信号占比过少将影响计算结果。

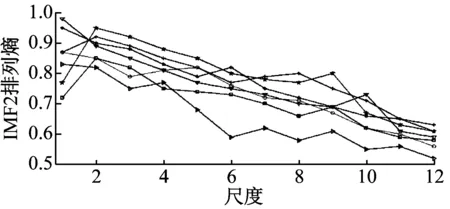
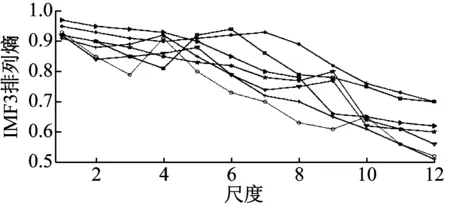


图8 各故障前四个IMF-VMD特征频率多尺度排列熵
Fig.8 The multiscal PE of first 4 IMF-VMD
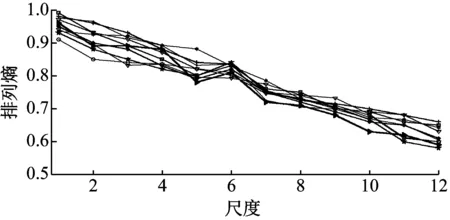
(a)

(b)图9 单一滚动体故障及三种复合故障多尺度排列熵Fig.9 The multiscal PE of the Rolling body crack and the Combination failure
4.3 ITSC方法验证
为验证原子区间平移稀疏编码(ITSC)效果,每类故障各取25个样本做识别,平移范围设为原子长度一半,以分析字典原子个数对分类识别率影响。因复合故障随机抽取的数据段中可能只出现单一故障波形,故此时分类到所属单一故障视为正确识别。对比结果如图10(a)和10(b)所示,观察字典尺寸,本文提出的ITSC方法在原子利用率上优势明显,在较少训练样本下通过原子平移和迭代寻找最佳匹配减小了训练样本提取压力,利用较少原子就能实现较高精度的匹配和分类。

(a)

(b)图10 采用ITSC前后字典尺寸与识别率的关系Fig.10 ITSC impact on dictionary size and recognition rate
4.4 分类效果对比
同一故障在100 km/h、150 km/h、200 km/h三种速度级下声发射信号存在一定差异,为进一步检验本文方法分类性能,对不同速度级下单一故障各取40组数据,复合故障各取80组数据进行分类试验,训练样本和待分类样本按3∶1划分。图11给出了几组待分类样本在不同正则化参数以及是否采用ITSC编码时稀疏系数分布和重构误差情况。
正则化参数ρ=0.6时采用ITSC获得七个正确分类结果,其中单一故障选中原子种类比复合故障少,整体误差也更小,分析原因是单一故障字典中原子少且匹配性能较好,复合故障受限于训练样本个数以及字典体积,在原子匹配和重构误差上会受影响。考虑声发射信号具有瞬时性和局部性,复合故障的故障点难以同时被传感器捕捉,此时基于排列熵的索引比对可能指向单一故障类字典。为验证此时分类性能,根据声发射冲击间隔和波形比对,对包含三种复合故障轴承截取一段只包含滚动体故障的数据,采用单一滚动体故障类字典作匹配,其稀疏系数分布见图第4行第3列。稀疏性较第3行单一故障差,原因可能是复合故障中其他缺陷产生的高频冲击信号并未完全衰减,存在波形叠加。试验中复合故障训练样本已经包含三类单一故障信号,所以分类结果并未出错,检验了方法的识别性能。

图11 稀疏系数分布和重构误差Fig.11 Sparse coefficient distribution and reconstruction error
进一步分析原子区间平移稀疏匹配问题,图中第3行第3列为常规方法计算的稀疏系数,在分类误差相近的情况下稀疏性明显较ITSC方法差。
分析正则化参数对组稀疏分类结果的影响,图中第4行圆点为正则化参数ρ=0且未采用索引字典计算的稀疏系数分布,此时重构精度较高,但原子选取类别跨度大。ρ=1时有最佳稀疏性(第6行方框),但重构误差较大。所以本文选取正则化参数为0.6以平衡组间稀疏性和重构性。
表2为三种速度级下几种分类方法对比,均采用基于最优一阶加速的组LASSO算法求解,运行CPU为2.4 G-I5,内存8 G。本文方法提取的原子单个原子长度较长,但字典原子数比采用Gabor原子学习字典少的多,原子匹配能力更强,稀疏性也更好,识别率明显高于Gabor字典。采用索引组合字典时,虽然需要计算数据排列熵,且增加了一个字典用于索引,但在未明显降低识别率情况下仍缩减了计算时间。通过结合本文提出的ITSC方法,分类整体计算时间虽有所增加,但识别精度显著提高,平均重构误差在所有方法中最低。
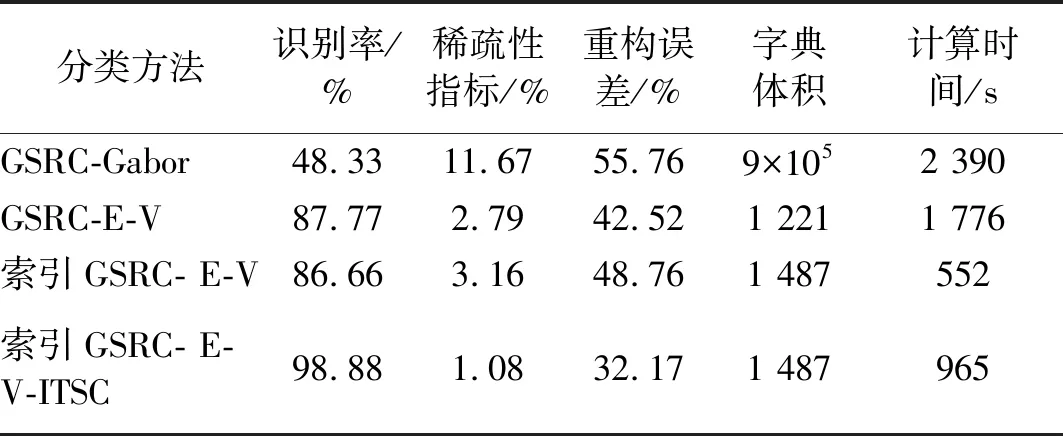
表2 几种方法分类对比Tab.2 Classification performance comparison
5 结 论
(1) 改进EEMD结合VMD方法能够自适应获得与故障信号高度相关的字典原子,相比传统字典构造方法能更好的保留故障信号内部信息。
(2) 多尺度排列熵能反应故障的内部信息,其构成的小体积索引字典能快速实现故障的预匹配,缩小故障类范围,从而加快分类速度。
(3) 原子区间平移稀疏编码算法可大幅扩展原子匹配性能,降低样本数据截取数量和截取要求,在字典紧凑性和分解稀疏性上优势明显。
(4) 本文提出的GSRC方法用于轴承故障声发射信号分类识别,无需复杂参数设置,对经验依赖小,实现了较高的分类精度。
