水下环肋圆锥壳临界压力—频率特性分析

张帅 ，李天匀*，3，郭文杰 ，朱翔 ，3，林子钦

1华中科技大学船舶与海洋工程学院，湖北武汉 430074

2船舶与海洋水动力湖北省重点实验室，湖北武汉 430074

3高新船舶与深海开发装备协同创新中心，上海 200240

4华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌330013

0 引 言

环肋圆锥壳的结构形式简单，且力学性能稳定，因而在工程建筑中得到广泛应用。通常，潜艇艉部可用环肋圆锥壳近似模拟。目前，国内外针对水下圆柱壳临界压力问题的研究已较为充分，而对水下环肋圆锥壳临界压力—频率特性的研究则相对较少。同时，由于环肋圆锥壳的几何特性较圆柱壳复杂，在实际工程应用中，求解环肋圆锥壳振动问题的难度较大。因此，针对水下环肋圆锥壳的临界压力—频率特性问题，开展理论研究具有重要的工程指导意义。

针对水下环肋圆锥壳体的振动问题，相关学者采用诸如有限元法、边界元法、能量法及解析法等对其进行了研究。Crenwelge等［1］根据应变—位移的关系，采用能量法分别求解了简支情况下圆锥壳加环肋和纵骨的自由振动特性。Arnold等［2］对两端简支及两端刚固的圆柱壳的振动特性进行了理论和实验研究。Tong［3］采用幂级数的形式，对正交各向同性及正交各向异性的圆锥壳的线性自由振动特性进行了研究。Irie等［4］使用迁移矩阵法分析了厚度可变的圆锥壳的自由振动特性。Yuan等［5］使用瑞利—里兹方法解决了圆柱板壳组合的振动特性问题。Lashkari等［6］针对锥柱组合壳，比较了有限元数值解与实验结果，发现结果吻合较好。Hu等［7］提出了一种综合理论分析和实验结果的方法来解决锥柱组合壳的载荷施加问题。Guo［8-9］研究了弹性波在真空圆锥壳内的传播和辐射特性，并采用摄动技术，以小顶角作为参数，分析了圆锥壳上波浪流体加载的影响。郭文杰等［10］采用镜像原理及加法定理，求解了有限浸深圆柱壳的振动特性。陈美霞等［11］采用幂级数法研究了不同边界条件下水中环肋圆锥壳的振动特性。

静水压力作用下结构稳定性及临界压力的测量一直是工程上比较关心的问题。刘硕刚等［12］采用试验与有限元相结合的方法，对静水压力作用下环肋圆柱壳在各振动模态下的结构固有频率进行了计算分析，给出了在静水压力下临界压力的判定方法。王宗利等［13］采用基于软件的数值分析方法，通过对耦合系统的建模与分析计算，讨论了不同水深的静水压力对水下结构自振特性的影响。陈忱等［14］提出了基于波传播法圆柱壳的临界载荷预报方法。李天匀等［15］采用Galerkin法求解了不同静水压力下的圆锥壳的频率特性。孟凡深等［16］采用波动法和牛顿迭代法，得到了不同边界条件下功能梯度圆柱壳的固有频率以及临界压力值。Liu等［17］分析了静水压力对水下环肋圆柱壳输入功率的影响。但目前针对水下环肋圆锥壳临界压力—频率特性的研究还较少。

本文拟基于Flügge壳体理论，将不同水深的静水压力代入壳体方程，得出静水压力与固有频率的关系以及环肋对水下圆锥壳承压能力的影响，然后考虑边界条件以及权函数的选取，从而求解临界压力—频率特性，为研究环肋圆锥壳临界压力振动频率问题提供新的思路。

1 理论分析

1.1 理论模型

如图1所示，截顶锥壳小端半径为R1，大端半径为R2，整个截顶锥壳长为L，壳体的厚度为h，半锥角为α，壳体质量密度为ρ，坐标s，θ，z分别为圆锥壳的母线方向、圆周方向和法线方向，位移分别为u，v，w，q为静水压力（当静水压力为外压时，q取负值）。

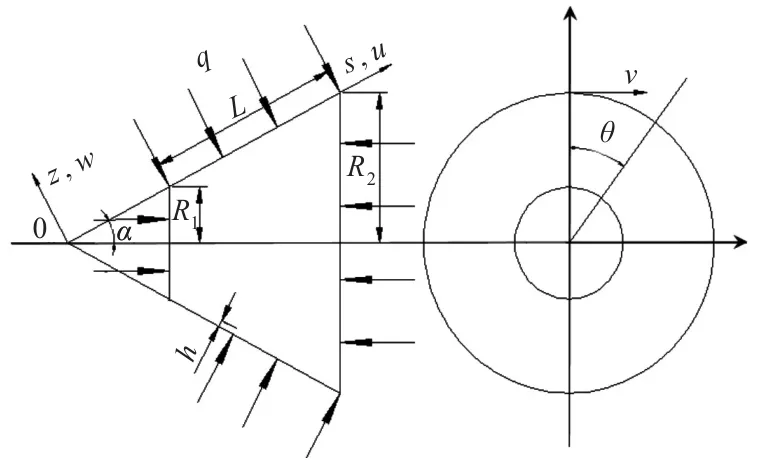
图1 截顶圆锥壳坐标系Fig.1 Truncated conical shell coordinate system

1.2 壳体振动方程

静水压力下的壳体振动平衡方程为［14，18］

式中：R为壳体中面半径；F1，F2，F3分别为轴向、周向和法向静载荷；Ns，Nθ，Nsθ，Nθs为单元内面力；Qs和Qθ分别为轴向和周向剪力；Pf为流体声载荷（动载荷）；ρ为壳体密度。

1.3 环肋的力学效应

环肋的力学效应主要体现为周向内力和内力矩的变化［19］：

图2 环肋示意图Fig.2 Schematic diagram of ring-stiffener

式（1）中的h用代换，=h+A/dL。

2 方程求解

对方程（1）进行变换，具体过程可参考文献［15］，得到如下矩阵：

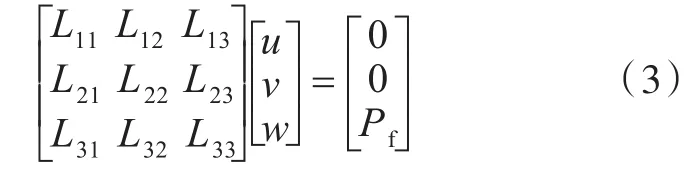
式中，L为壳体方程的微分算子，具体表达式可参考文献［14］。

目前，方程（3）还没有准确的解析解，故此处采用Galerkin法进行近似求解。

为了求解方程（3），需要作出一些假设：

1）构造一个满足边界条件的位移型函数；

2）当圆锥壳两端简支时，满足v=w=Ns=Ms，其中Ms为未加环肋壳体单元内弯矩。

满足上述假设条件的型函数可写成

式中：n为周向波数；m为轴向振动波数；ω为圆频率；U，V，W分别为轴向、周向和法向的位移幅值。

将方程（4）代入方程（3），变换可得

其中，

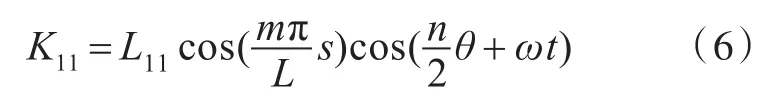
在使用加权残值法之前，还需要选取残值函数以及权函数。令式（5）左边的函数为残值函数，令除去广义位移幅值U，V，W的权函数为型函数，然后使用Galerkin法进行积分：

对式（7）进行积分变换，采用矩阵的形式表示为

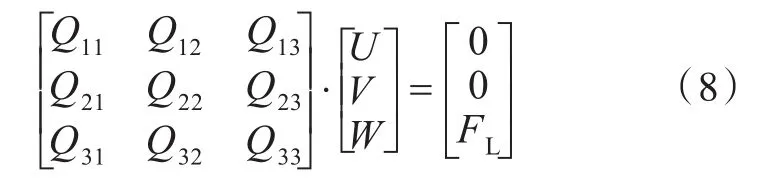
式中，FL为流体载荷积分的贡献项。FL的表达式为

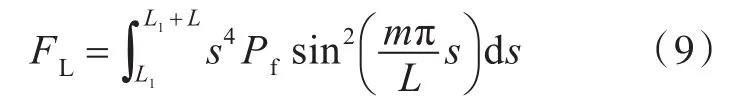
式中，L1为圆锥壳分段后第1段的长度。

根据文献［10］，可采用小顶角作为参数来求解圆锥壳上的波浪载荷。

理想流体在柱坐标下的Helmholtz波动方程为

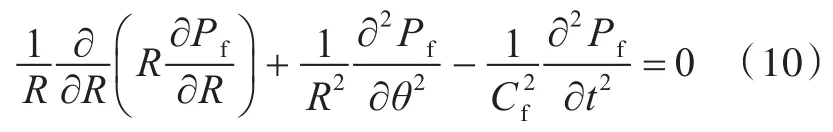
式中，Cf为流体中的声速。

根据声学边界条件可知，流体与壳体在其接触面上必须满足二者的径向速度相等，即

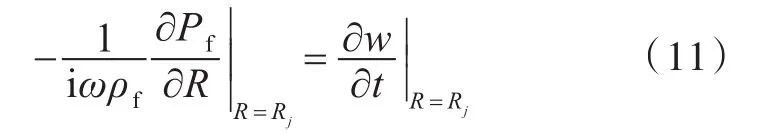
式中：ρf为流体密度；Rj为第j个圆柱壳微段。

根据文献［10］提出的求解方法，可由式（10）和式（11）求解第j个圆柱壳微段的Pf：

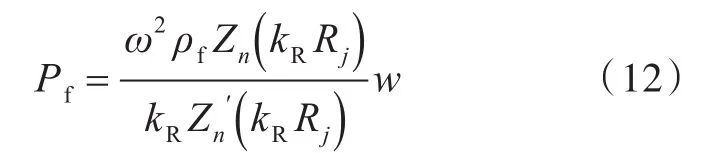
式中，kR为径向波数。在求解kR时，需引入变量kf和k，其中，为流体中的自由波数，，为轴向波数。如果kf＞k，则，这时为第1类汉克尔函数。如 果kf＜k，则，这时Zn()=Kn()，Kn()为第2类贝塞尔函数。

将圆锥壳分解为a个小圆柱壳微段，对流体声载荷积分贡献项FL进行数学变换，可写成如下形式：

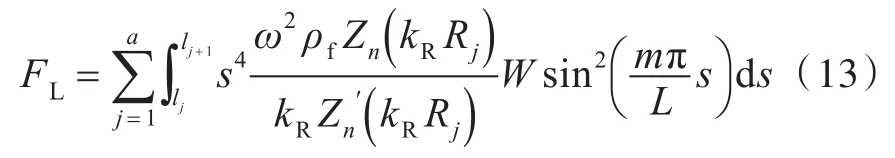
式中，lj为圆锥壳第j段。

计算表明，a=20时的收敛性很好，所以

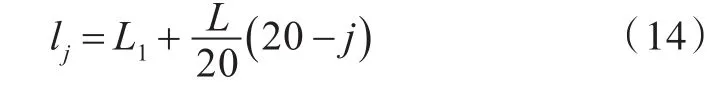
将方程（13）代入方程（8），可得

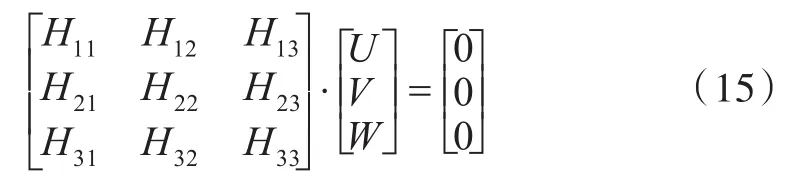
求解方程（15），即可得到环肋圆锥壳的固有频率。

3 环肋圆锥壳算例分析

3.1 方法的准确性分析

圆锥壳的具体参数如下：R1=1 m，R2=R1+Lsinα，L=2 m，L1=R2/sinα-L，h=0.01 m，α=10°，30°，50°，ρ=7 850 kg/m3，E=2.1×105MPa，ρf=1 000 kg/m3，Cf=1 500 m/s，qcr为临界压力。通过上述参数可以求得圆锥壳的无量纲临界压力。根据文献［20］可知，圆锥壳最小的无量纲临界压力如表1所示。

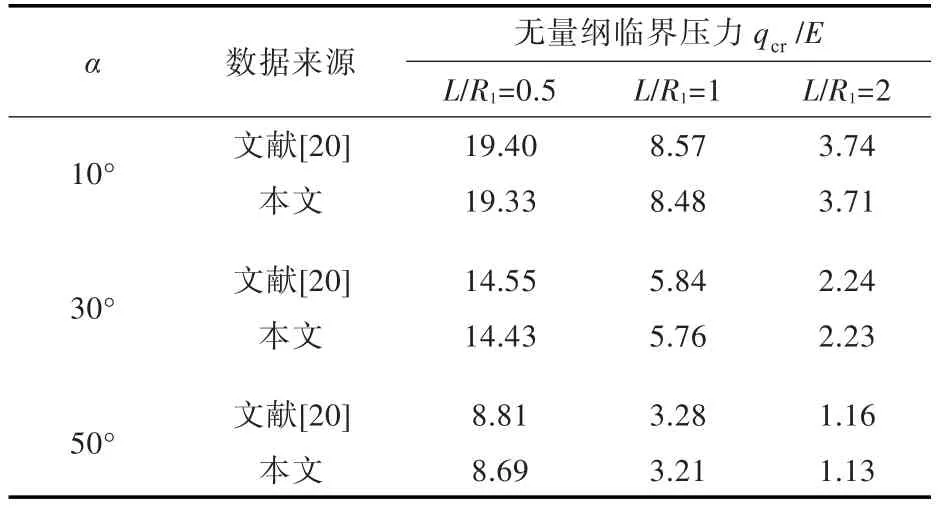
表1 无量纲圆锥壳临界压力值对比Table 1 Comparison of critical pressure values of dimensionless conical shells

由表1可知，本文计算得到的数据与参考文献［20］的数据误差很小，证明了本文计算方法的准确性。另外，分析表中数据可得：

1）当半锥角不变时，临界压力与L/R1的比值呈线性负相关，表明临界压力随壳体长度的增加而减小；

2）当L/R1不变时，壳体半锥角越大，临界压力越小。

3.2 环肋对结构承压能力的影响

圆锥壳基本参数选取不变，环肋的参数为：Er=1.6×1011Pa，br=0.01 m，hr=0.02 m，dL=0.04 m，共有50个环肋。通过计算，确定环肋圆锥壳基频时的模态数为m=1，n=12。由图3可以看出，环肋圆锥壳固有频率（f）的平方和静水压力呈近似线性关系。这是由于水下环肋圆柱壳可近似为类梁结构，而轴压梁固有频率的平方和轴向压力呈现近似线性关系［21］，因此他们的关系也适用于水下环肋圆锥壳。

图3 环肋固有频率与静水压力的关系Fig.3 Relationship between natural frequencies and hydrostatic pressure in ring-stiffener

由图4可知，线性拟合求得环肋圆锥壳临界压力值为2.076 MPa，与无环肋时的临界压力值0.467 8 MPa［15］相比显著增大，说明环肋可以显著增强圆锥壳体的承压能力。

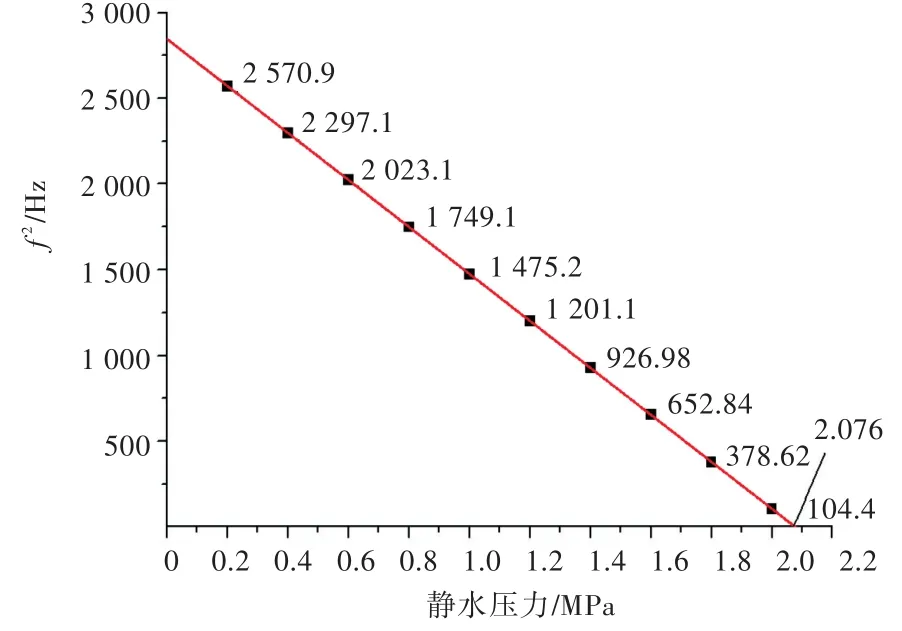
图4 环肋圆锥壳临界压力的计算Fig.4 Calculation of critical pressure of ring-stiffened conical shell

当圆锥壳基本参数不变，分别改变环肋的1个参数（从Er，br，hr中选择），保持另外2个参数不变，得到的无量纲临界压力qcr/E随参数的变化情况如表2所示。

由表2中数据可知，临界压力与Er，br和hr正相关，随其值的增大而增大。因为这3个参数增大时，整个壳体的刚度也会随之变大，壳体的承压能力随之变强。

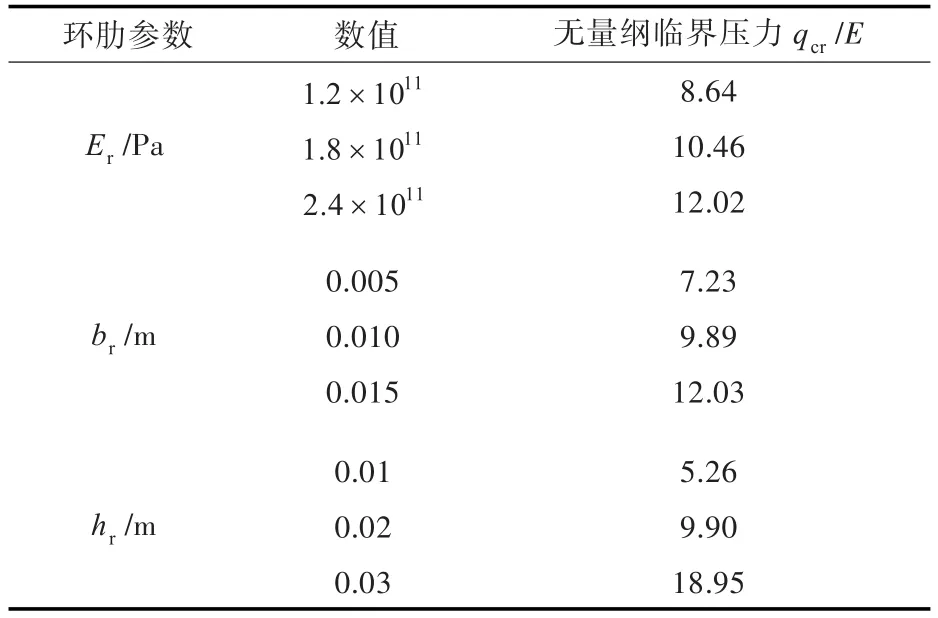
表2 随参数变化的环肋圆锥壳临界压力无量纲值（m=1，n=12）Table 2 The non-dimensional value of the critical pressure of the ring-stiffened conical shell with variable parameters（m=1，n=12）

3.3 环肋对固有频率的影响

圆锥壳基本参数不变，分别改变环肋的1个参数（从Er，br，hr中选择），保持另外2个参数不变，此时选取环肋圆锥壳基频的模态数为m=1，n=16，得到的固有频率f随参数的变化值如表3所示。

表3 随参数变化的环肋圆锥壳固有频率值（m=1，n=16）Table 3 The natural frequency value of the ring-stiffened conical shell with variableparameters（m=1，n=16）

通过表3的计算结果可知，环肋对固有频率的影响显著。当环肋的弹性模量Er增大时，固有频率会随之增大；当br和hr变大时，固有频率均会随之增大。表2和表3中的数值是在环肋圆锥壳两端简支的情况下计算得到的。通过分析这些数据可知，对环肋相关参数的设计以及经过修正以后得到的临界压力值，可以用于工程设计及评估。

4 结 语

本文结合波传播法及Galerkin法计算了水下环肋圆锥壳的临界压力和固有频率。建立了考虑静水压力的圆锥壳振动方程以及环肋力学平衡方程，采用线性拟合的方法得到了临界压力。研究结果表明，任意模态下水下环肋圆锥壳固有频率的平方随静水压力的增大呈近似线性递减的关系，并由此可以得到临界压力，经过修正，可以将其用于工程设计及评估中。对比结果证实了本文理论方法的可靠性，这为水下环肋圆锥壳临界压力的无损预报提供了新的求解方法与思路。