基于线性自抗扰控制的放卷张力控制系统

马宏帅，赵世海

（1.天津工业大学机械工程学院，天津 300387；2.天津市现代机电装备技术重点实验室，天津 300387）

放卷部分是连续轧染机的关键部分，放卷是织物在连续轧染上运行的第一步，其对张力控制的精度要求很高，如果放卷过程中张力出现波动，将会对后续加工的各个阶段造成影响，以至于影响织物的加工质量[1]。由于放卷过程中卷径不断变化，引起放卷辊转动惯量的变化，导致织物受到的张力也不断变化[2]。放卷系统是一个典型的时变性、非线性的耦合系统，因此，设计一个能够解耦并且具有良好抗干扰性能的控制器至关重要。

随着织物染整工艺的复杂化和多样化，对连续轧染机的加工质量要求越来越高，对放卷系统的张力控制器提出了更高的要求，常规PID控制器已经无法满足现代织物的加工要求。李革等[3]提出模糊神经网络的PID 控制方法，应用于带材的卷绕张力控制系统，使张力控制系统有较好的自适应性。李坤全等[4]提出自适应模糊PID控制方法，应用于瓦楞纸放卷张力控制系统，实现张力的稳定控制。张永胜等[5]提出模糊理论，用于同步带恒张力控制系统中，取得了较好的张力控制效果。但这些方法都要求建立精确的数学模型，对于复杂系统来说，影响因素多，建立精确数学模型比较困难。

本研究提出采用线性自抗控制方法[6-8]，不需要知道被控系统的精确模型和内外部扰动规律，利用张力扩张状态观察器，对被控系统的内外扰动进行估计并补偿。该方法不仅具有自抗扰控制器的功能，而且克服了自抗扰控制算法参数难整定的问题[9-11]，便于应用于实际工况中。

1 放卷系统数学建模

放卷系统由放卷辊和卷径测量装置组成，放卷辊由变频器电机驱动，通过PLC 发送指令控制变频，实现放卷辊的控制。放卷系统结构如图1所示。

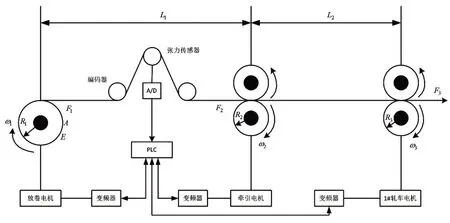
图1 放卷张力系统结构图

图1中E为织物的弹性模量；A为织物的横截面积；Ri第i个辊筒的半径；ωi(t)为第i个轧辊的角速度；F1为织物初始张力，F2放卷张力；F3为牵引张力；Li（i=1、2）为各轧车间的距离。

在放卷过程中，织物受到的张力主要来源与放卷辊与牵引辊之间的相互作用，假设织物只发生弹性变形，根据胡克定律织物所受张力可以表示为：

式中：ω为织物在两个辊之间的运行的时间。

假设织物与轧辊之间的运动为纯滚动，根据牛顿运动定律，所有轧辊符合下列式子的运动规律，即：

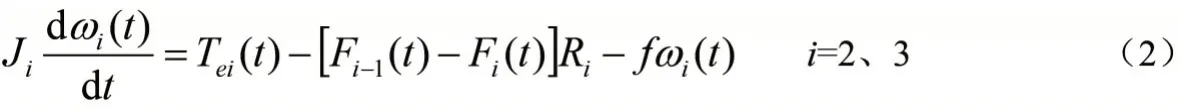
式中：Ji为第i个滚筒的转动惯量；Tei(t)为第i个电机的电磁转矩；Fi-1(t)、Fi(t)为前、后单元间织物的张力；为织物与辊筒间的摩擦阻尼系数。

对（2）式F2(t)、F3(t)求二阶导数，并将式代入，化简可得：

式（3）为放卷张力系统的数学模型，从该模型可知，放卷单元和牵引单元都可以建立二阶微分方程。由于放卷辊卷径的时变性会引起张力的变化，而且放卷单元张力的变化会引起后续加工段织物张力的变化，该系统是时变性、非线性二阶耦合系统。

2 模型解耦与线性自抗扰控制器设计

2.1 静态解耦

根据放卷张力系统模型，Te1(t)、Te2(t)为系统的控制输入；F2(t)、F3(t)为系统的输出；可以得出系统的空间状态模型为：

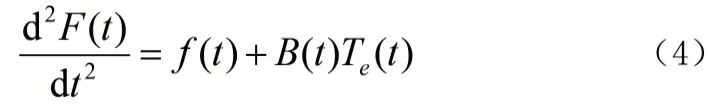
式中：f(t)为动态耦合矩阵，B(t)为静态耦合矩阵，其表达式为：

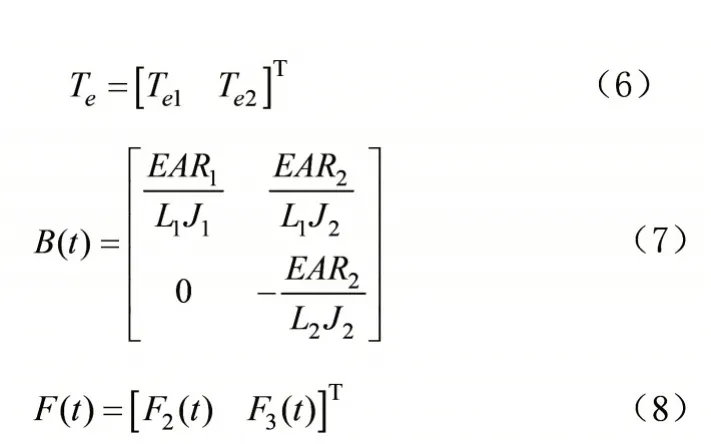
引入虚拟控制量U(t)，令U(t)=B(t)Te(t)，代入式中，可得：

因|B(t)≠0|，所以Te(t)=B(t)-1U(t)，B(t)-1为静态解耦矩阵，可以表示为：

在系统空间状态方程中引入虚拟控制量U(t)后，使放卷系统的放卷单元和牵引单元成为单输入、单输出的一阶系统，实现了系统的静态解耦，只需对系统的动态扰动（包括未建模部分、参数变化扰动等）进行估计补偿就可以实现放卷张力的系统的完全控制。

2.2 动态解耦

线性自抗扰控制器的核心部分为线性扩张状态观察器（LESO），能够对系统中动态耦合部分、由参数变化以及外界条件引起的扰动进行估计并进行补偿。针对放卷张力系统的数学模型，设计线性扩张状态观察器（LESO），对该系统的状态变量进行估计，即：

式中：ei为系统输出Fi的估计误差；z1i为Fi的估计值，z2i为F&i的估计值，z3i为f(t)的估计值；ω1i、ω2i、ω3i为增益系数；h为积分步长。通过调整ω1i、ω2i、ω3i增益参数，使得z1i、z2i、z3i分别无限接近Fi、F&i、f(t)。即设计动态误差补偿量为：

式中：U0i(t)为动态误差反馈控制量。

将式（12）代入式（9）可得：

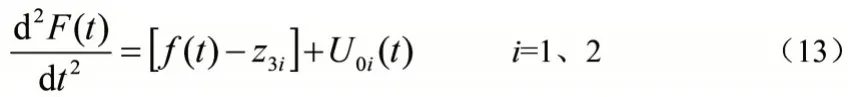
通过线性扩张状态观察器（LESO）中z3i对放卷张力系统中总扰动的估计，可以补偿各单元中动态耦合的总扰动，能够解决该系统中动态耦合的问题。在线性自抗扰控制器设计中，为了避免跟踪误差引起的张力波动，采用PD 控制对放卷张力系统的个单元进行控制。PD控制器为：

式中：F0i为各单元张力参考值；kpi、kdi为各单元控制器增益系数；ω为期望闭环的阻尼系数；为控制器的可调参数。

根据放卷张力系统各单元的数学模型，对模型进行静态解耦和动态解耦，设计线性自抗扰控制器，将非线性、时变性的耦合二级系统转化为单输入、单输出的线性系统。该系统的控制结构图如图2所示。

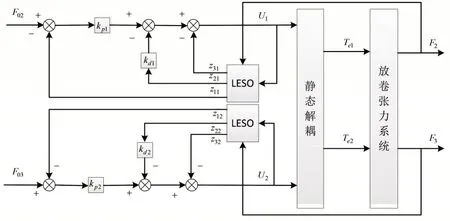
图2 线性自抗扰控制结构图

3 仿真分析

针对放卷张力系统设计的线性自抗控制器，进行仿真实验研究。在MATLAB/Simulink 中建立放卷系统的模型和线性自抗扰（LADRC）控制器模型[12]，对该控制器在解耦和抗干扰方面的控制效果进行验证，并且与常规PID 控制器的控制效果进行对比分析。放卷张力系统模型参数如表1所示，控制器参数如表2所示。

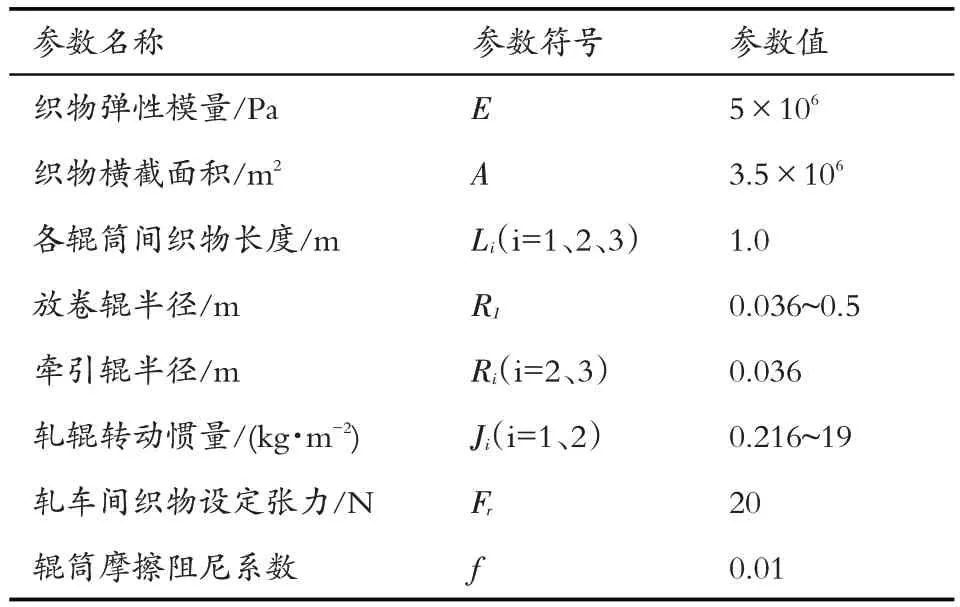
表1 放卷张力系统模型参数表

表2 控制器参数表

3.1 解耦仿真对比

在连续轧染机实际工作过程中，对织物的加工是连续的，放卷单元是加工的一步。这个阶段织物张力需要按照织物的加工工艺进行设定和调整，根据放卷张力系统模型的分析，该系统中放卷单元和牵引单元中织物张力具有耦合作用。

在1#轧车辊筒的角速度ω3=100 rad/min，放卷辊的半径R1=0.3 m，分别调整放卷单元F2=22 N和牵引单元F3=20 N，稳定运行4 s 后，将F2调整到27 N，保持2 s 后，恢复到22 N。在不同控制器下解耦曲线如图3所示。

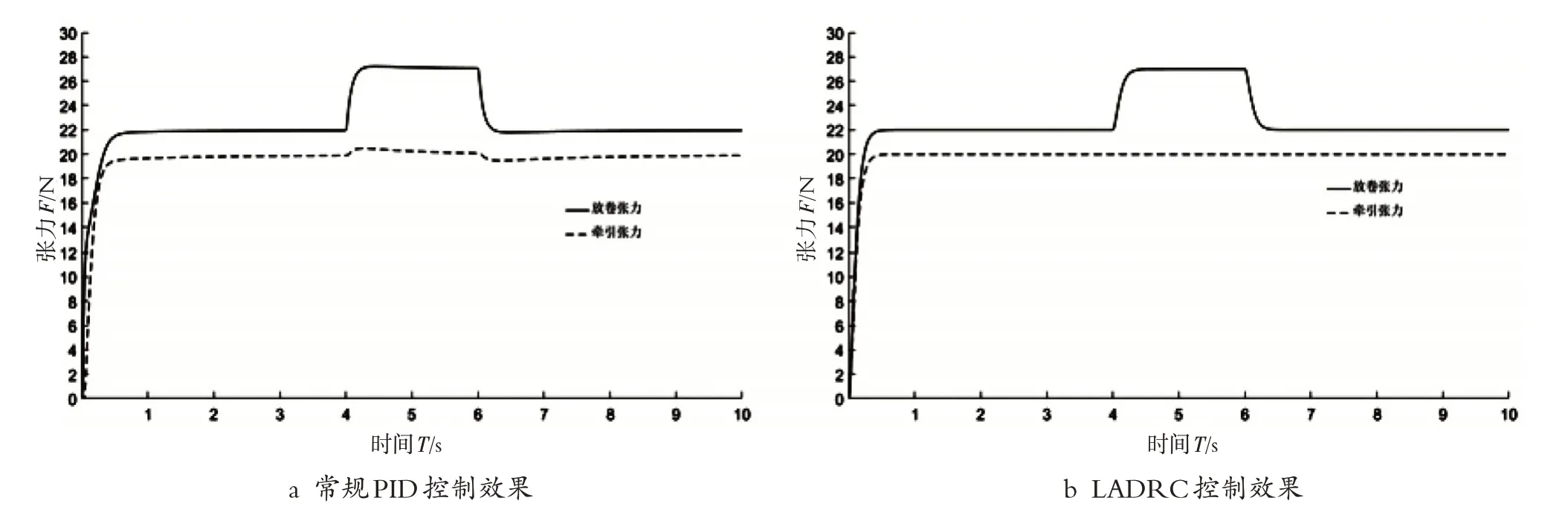
图3 不同控制器的解耦仿真曲线

由图3可以看出，在常规PID 控制器下，F2在4 s和6 s时的变化，会引起F3有0.85 N的波动，而在线性自抗扰控制器（LADRC）下，F2的变化，不会引起的波动；说明该控制器解决了放卷单元和牵引单元张力耦合问题，具有良好的解耦效果。

3.2 抑制参数扰动仿真对比

放卷系统在实际运行过程中，放卷辊的半径不断变化，会引起放卷张力的变化。在ω3=100 rad/min，放卷辊半径分别为0.1、0.3、0.5 m时，两种控制器对放卷张力F2的控制效果如图4所示。在R=0.3 m，1#轧车电机的角速度分别为100、120、150 rad/min 时，两种控制器对牵引张力F3的控制效果如图5所示。

图4 R变化，F2仿真曲线

图5 ω3变化，F3仿真曲线

由图4可以看出，当放卷辊的卷径发生变化时，在常规PID 控制器控制下，放卷张力F2达到20 N 的时间延长，还产生5.6%超调，需要重新整定PID系数，才能保证系统稳定；但在线性自抗扰控制器（LADRC）的控制下，F2不受卷径变化的影响，能够迅速稳定达到20 N。由图5可以看出，当1#轧车电机的角速度发生变化时，在常规PID 控制器控制下，牵引张力F3会产生15.8%的超调，使系统不稳定，而在线性自抗扰控制器（LADRC）的控制下，F3不发生明显变化；说明LADRC具有良好的抗内部参数扰动效果。

3.3 抑制外部扰动仿真对比

在实际生产中，放卷会受到外界条件的影响，利用正弦扰动和方差为0.001的噪声信号模拟未知干扰和外界干扰，两种控制器对放卷张力的控制效果如图6所示。由图6可以看出，放卷系统在受到外界干扰和未知干扰的情况下，在常规PID 控制器控制下，放卷张力F2发生明显的波动，造成系统不稳定，而在线性自抗扰控制器（LADRC）的控制下，F2受外界扰动的影响很小，能够保持系统稳定运行。说明LADRC具有良好的扰动补偿和抗干扰性。

图6 外界扰动，F2仿真曲线

4 结论

针对连续轧染机放卷张力系统对张力稳定性的要求，提出采用线性自抗扰控制器（LADRC）控制的方法，解决了因放卷张力与牵引张力的耦合以及参数扰动和外界干扰引起张力变化的问题，使放卷系统能够稳定运行。通过与常规PID控制器对比仿真实验，LADRC体现出对放卷模型参数变化和外界干扰的鲁棒性和控制精度以及良好的解耦效果。该控制器参数调节少，调节方便，具有一定的实用价值。