基于改进的K-means算法在文本挖掘中的应用

杨 丹，朱世玲，卞正宇

(南京邮电大学 计算机学院，江苏 南京 210003)

0 引 言

K-means算法作为一种无监督的机器学习算法[1]，具有简单易理解、聚类速度快等特点。目前聚类算法大致可以分为基于划分的、密度的、分层的、网格的、模型的等类型[2-6]。虽然K-means算法在众多领域应用广泛，但是其聚类质量的优劣则取决于多个因素。针对K-means算法对于初始聚类中心选择的敏感性，文献[7-8]提出了一种基于最大最小距离法选取初始聚类中心的方法，该算法基于距离最远的数据对象最不可能分到一个簇的事实，获取若干个距离彼此相隔较远的点作为初始中心[9]。虽然该算法的聚类效果相对于传统算法有了一定的提高，但是并没有考虑到距离较远的数据对象可能是离群点的情况，离群点作为初始聚类中心会影响到聚类的最终结果[10]并且也会增加迭代的次数。

在上述算法的基础上，文中依据稀疏度能够度量点周围紧凑程度的特点[11-12]，结合最大最小距离法的原理，提出了一种新的结合稀疏度和距离的方式来选择初始聚类中心，并通过实验对该算法进行验证。

1 稀疏度

在数据集D{x1,x2,…,xn}中,对象F的稀疏度定义为：

(1)

其中，Ni表示xi的K个近邻对象组成的对象集合；d(xi,xj)表示xi,xj之间的距离。

2 K-means算法

2.1 基本思想

给定一个数据集D{x1,x2,…,xn},每一个数据对象都是m维的，将数据集D划分为K个簇{S1,S2,…,SK}，使用K-means算法过程需要使用的定义如下：

定义1:两个数据对象之间的距离(欧氏距离)。

(2)

其中,xi,xj为数据集中的两个数据对象。

定义2:聚类中心。

(3)

其中，nc表示簇C包含数据对象的个数；xi表示簇C的第i个数据对象。

定义3:聚类的终止条件。

(4)

其中,K表示簇的个数;Zj表示第j个簇的中心;nj表示第j个簇包含的数据对象的个数。

定义4:Minps值。

(5)

(6)

上述公式都是一种经验的规则，xi邻近的Minpts个点组成Ni，Kmax表示最大的聚类簇数，beta为用户自定义的参数。

算法1：K-means算法。

输入：数据集D，簇的个数K，聚类终止条件E，迭代次数T

输出：K个满足终止条件和迭代次数的簇

Step1：在数据集D中任选K个初始聚类中心；

Step2：循环Step3～Step5，判断是否满足终止条件E和迭代次数；

Step3：按照定义1计算剩余的数据对象到每个聚类中心的距离，将其归并到距离最小的簇中；

Step4：按照定义2，重新计算每个簇的聚类中心；

Step5：按照定义3，计算聚类结果E。

2.2 改进的K-means算法描述

对于初始聚类中心的选择，不仅要考虑到初始聚类中心周围的紧密程度，而且还要保证初始聚类中心尽量的离散。因此文中在采用稀疏度评判数据对象周围稀疏度的同时，为了保证聚类中心点尽量离散，采用了一种新的结合稀疏度和距离的度量方式。首先通过稀疏度来判断数据周围的紧密程度，然后结合最大最小距离的原则构建一个新的评价函数。该评价函数可以有效避免文献[10]必须人为确定参数的缺点，使得初始聚类中心的选择更加稳定。评价函数如下：

(7)

其中，S(xi)表示数据对象xi的稀疏度；D(xi)表示数据对象xi与其他已选初始聚类中心距离的最小值；Si的值是介于-1和1之间。Si接近1时，表示数据对象xi的周围是紧凑的，且远离其他的聚类中心。

改进的算法流程如下：

输入：簇的数目K，数据集D，最大迭代次数T及终止条件E

输出：K个满足终止条件和迭代次数的簇

Step1：按照式1～5，计算每个数据对象由Minpts个点组成的对象集合的稀疏度，选择稀疏度最小点作为第一个初始聚类中心；

Step2：按照式7计算剩余的数据对象与已选取的初始聚类中心值，选取值最大的点作为剩余初始聚类中心，依次循环下去，直到满足K个初始聚类中心；

Step3：利用K个初始聚类中心进行聚类。

3 文本聚类

3.1 TF-IDF算法

文本表示常用的模型有布尔逻辑模型(BM)、向量空间模型(VSM)[13-15]、潜在语义索引(LSI)[16]和概率模型(PM)等。文中采用的是向量空间模型，对于文档D，采用(TF-IDF1,TF-IDF2,…,TF-IDFn)来表示[17-19]。IF-IDF算法公式如下：

TF-IDF(ti,d)=

(8)

其中，ni为含词条ti的文档数；N为文档总数。

3.2 改进的文本距离计算

K-means算法通常是根据两个数据对象之间的距离来归类的[20-22]。但在对文本进行聚类之前，通常采用余弦公式来计算两个文本间的相似度。文中根据相似度值总是处于0和1之间的特点，采取一种简单的数学变化将文本相似度转化为文本距离，避免文献[8]采用lg方法需设计参数的问题，距离公式如下：

余弦计算公式：

(9)

距离计算公式：

Distancei,j=1-cosθ

(10)

其中，vi和vj分别表示两个文本特征向量，在距离公式中，当两个文本的相似度为1时，距离为0；当两个文本之间相似度为0时，两者之间的距离最大为1。

4 实验结果与分析

4.1 实验一

4.1.1 实验结果

实验环境：Window7操作系统，1T硬盘，MyEclipse软件，Java编程软件。

实验数据：为了验证改进后的算法优于传统算法和文献[4]算法，采用了UCI数据库中的3个数据集：Iris、Wine及Balance-Scale。其中Iris数据集包含4个属性，150个数据对象，分为3类；Wine数据集包含13个属性，178个数据对象，分为3类；Balance数据集包含4个属性，625个数据对象，分为3类。

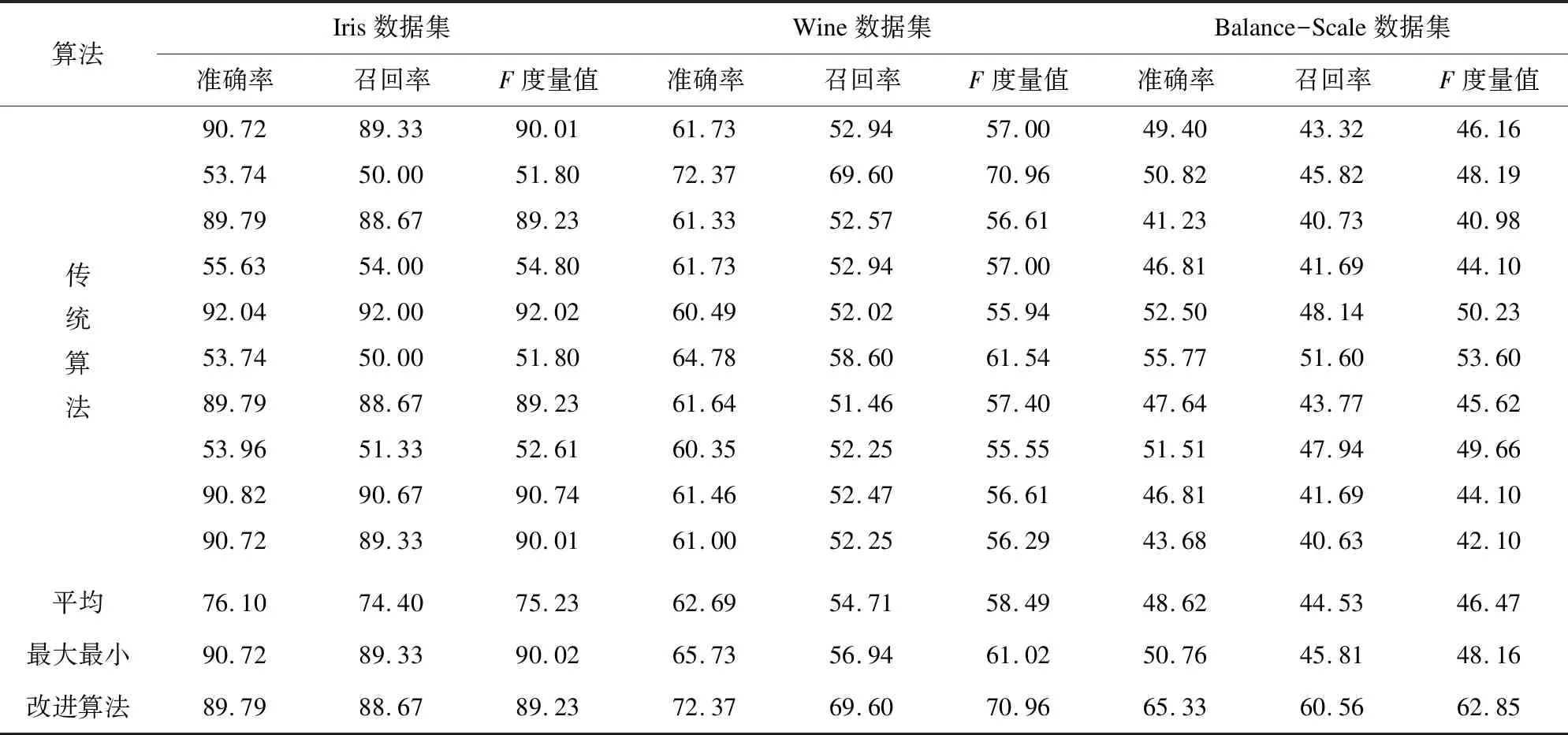
实验结果：实验通过准确率、召回率及F度量值对传统算法、最大最小距离法及改进后的算法进行了比较，结果见表1。

表1 算法比较(1)

%

4.1.2 实验分析

根据表1的实验结果可以看出，传统算法在Iris数据集的10组实验结果中，准确率、召回率及F度量值中最高值与最低值都相差30个百分点以上，在Wine数据集上，三个度量值中最高值与最低值相差也在15个百分点以上。在相差值较小的Balance-Scale数据集中三个度量值的最高值与最低值相差也达到了10个百分点左右。因此传统算法的聚类结果的随机性很大，很不稳定。

最大最小距离法相对于传统算法在Iris数据集上的准确率、召回率及F度量值都优于传统算法,但是在Wine、Balance-Scale数据集上聚类效果略低于传统算法。首先对Wine数据集进行分析，可以发现该数据集的最后一个属性值的范围跨度较大，最大值为1 680，最小值为278，采用最大最小距离法选取初始聚类中心会受到最后一条属性的影响，因此所选取的聚类中心不能很好地代表数据的实际分布。其次再对Balance-Scale数据集进行分析，可以发现它的分布极度不均匀，最大的簇包含288个数据对象，而最小的簇仅仅包含49个数据对象，如果仅仅采用最大最小距离法选取初始聚类中心，可能会导致所选取的中心来源于某一个或其中的某几个簇。

文中改进算法是在最大最小距离乘积法的基础上，采用稀疏度来评判所选取的聚类中心，既考虑到了数据的分布情况，又使所选取的聚类中心较远。从实验结果来看，该算法无论是在分布均匀的数据集中，还是在分布不均匀的数据集中，聚类的准确率、召回率以及F度量值都优于传统算法和最大最小距离算法。

4.2 实验二

4.2.1 实验数据

为了证明改进后的算法聚类结果的优越性，实验数据采用了搜狗语料库中的财经文档150篇，教育文档500篇和军事文档350篇。通过准确率、召回率及F值对实验结果进行分析，比较算法的聚类效果。其中传统算法的值为5次实验结果的平均值。实验结果见表2。

4.2.2 实验分析

由于文本具有高维稀疏的特点，所以文本聚类的效果并不像普通数据集那样产生较好的结果。针对文本聚类过程中不可以采用簇的均值替代新的聚类中心的原理，采用K-中心算法中计算新的中心点的方法来获取迭代中的中心点。通过表2可以看出，改进算法相较于传统算法和最大最小距离法在聚类质量上都有了一定的提高，因此，该算法相较于传统算法和最大最小距离法较适合用于进行文本聚类。

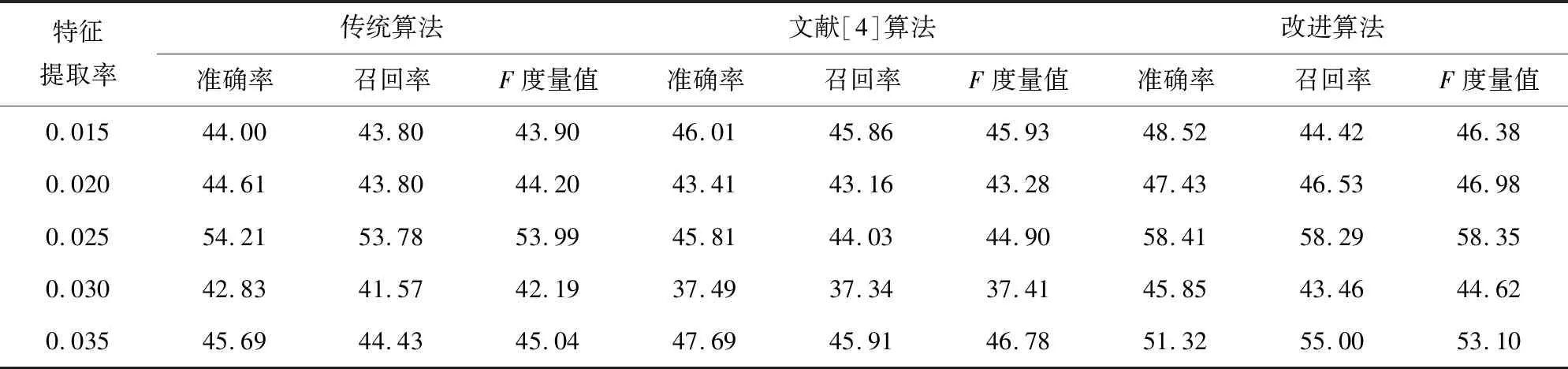
表2 算法比较(2)

5 结束语

针对K-means算法相较于其他聚类算法具有对初始中心敏感的特点，结合最大最小距离的方法提出了一种基于稀疏度选取初始聚类中心的算法。实验结果表明，该算法优于传统的K-means算法和最大最小距离算法，并得到较好的聚类效果。最后将该算法应用于文本的聚类处理中，在聚类的过程中通过一个简单的变换将相似度转化为对象之间的距离值。实验表明该算法相较于传统算法和最大最小距离法更加适用于文本聚类处理，准确率和召回率和F度量值都有了一定的提高。