基于粒子群的多标记阈值自适应极限学习机

许二戗，于化龙

(江苏科技大学 计算机学院，江苏 镇江 212003)

0 引 言

众所周知，在传统的监督学习框架中，数据集中的每个样本通常只关联于一个标记，但在现实应用场景中，一个样本则通常可能关联多个标记，此种类型数据被称为多标记数据。在近十几年中，多标记学习已逐渐发展成为机器学习领域的研究热点之一，吸引了大量研究者的关注，并在多媒体内容自动标注[1]、信息检索[2]、个性化推荐[3]、生物信息学[4]等多个领域得到了实际的应用。

在多标记数据中，普遍存在着类别不平衡的现象，其表现为在绝大多数或全部标记中的正类样本个数远少于负类样本个数。类别不平衡问题往往会导致所训练的分类超平面产生严重偏倚，从而降低多标记算法的最终分类性能。为解决上述问题，Charte等[5-6]将单标记类别不平衡学习中的ROS、RUS及SMOTE等采样技术扩展到多标记数据中，分别提出了ML-ROS、ML-RUS、ML-SMOTE等算法；Zhang等[7]则在算法层面进行了改进，通过结合样本相关性及集成学习技术提出了COCOA算法。但上述算法仍存在着分类性能差或时间复杂度高等诸多缺点。

极限学习机(extreme learning machine，ELM)是2006年黄广斌等[8]提出的一种单隐层前馈神经网络训练方法，具有训练速度快、泛化性能好等优点。ELM在回归、聚类、二类分类和多类分类等领域都有不错的表现[9]，但目前在多标记领域的应用仍相对较少，同时也未考虑到多标记数据中的不平衡现象。

鉴于ELM技术的诸多优点，拟结合其与类别不平衡学习中常用的阈值选择技术，提出一种适用于多标记不平衡数据的自适应阈值极限学习机(PSO-based multi-label threshold adaptation extreme learning machine，MLTA-ELM)算法。首先，该算法通过建立ELM模型来获得样本标记的预测输出值；然后，选定合适的阈值组合对其进行标记判别。在进行阈值选择时，原有问题转化为一个多变量优化问题，故文中利用粒子群优化算法作为阈值选择器。当然，也可以尝试采用其他随机优化算法来替换PSO算法。最后，利用12个基准的多标记数据集对该算法的性能进行了验证，并与5种基准或流行的算法进行了比较。

1 相关工作

1.1 多标记中的类别不平衡问题

在多标记学习领域中，已存在多种成熟的算法，如ML-KNN[10]、IMLLA[11]、BP-MLL[12]、RAkEL[13]等，但大多算法仍主要关注于如何挖掘标记间的相关性，而忽略了多标记数据中往往存在类别不平衡问题这一特点。因此，下面将以标记密度与不平衡比率这两个评价指标来简单介绍多标记数据中存在的类别不平衡问题。

标记基数(label card，LCard)表示每个样本所对应正类标的均数，而标记密度(label density，LDen)则表示每个样本所对应正类标在所有类标中所占的比例，如一个多标记数据集的LDen测度值为0.2，则表示每10个类标中平均有2个被标记为正类，上述测度可通过如下两个公式计算得出：

(1)

(2)

其中，N表示样本数；|Yi==1|表示第i个样本所对应类标被标记为1的数量；|y|表示类标的个数。

表1统计了在后续实验中使用的12个数据集的特征信息，从中可以看出：仅有flags数据集的标记密度接近0.5，其余的均在0.33以下，且大部分在0.2左右。这说明多标记数据集中的正类标记所占比例均相对较低。

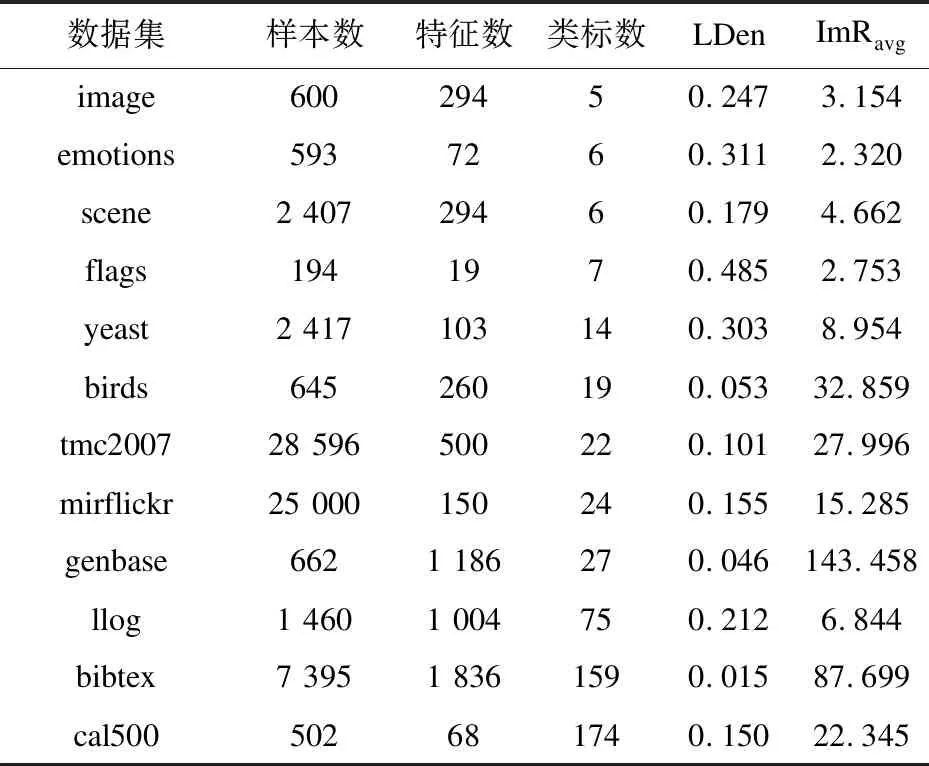
表1 所用数据集及其不平衡测度

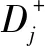
(3)

对于多标记数据集，不平衡比率的算术平均值ImRavg能够直观地反映出其类别偏倚的程度。从表1可明显看出，所有数据集的不平衡比率均处于2.2～143之间，其中8个数据集不平衡比率大于5，6个数据集的不平衡比率在10以上。总体而言，类别不平衡普遍存在于多标记数据中，且类标越多，极度不平衡现象出现的可能性也通常越高。

1.2 极限学习机

极限学习机是一种单隐层前馈神经网络(single hidden-layer feedback network，SLFN)训练方法[8]。其完全摒弃了传统的迭代误差调整策略，改为随机设置隐层权重与偏置，然后利用最小二乘的思想直接对输出层权重矩阵进行求解，只需要很少的训练时间，即可获得同等或更优的泛化性能。

不妨假设训练集包含N个样本，且这些样本能被分入m个类中，第i个训练样本表示为(xi,ti)，其中xi是一个n维的输入向量，而ti则对应于一个m维的输出向量。另假设ELM中包括L个隐藏层节点，该层上的权重w与偏置b在[-1,1]区间完全随机生成，那么对于样本xi，其对应的隐藏层输出可以表示为一个行向量h(xi)=[h1(xi),h2(xi),…,hL(xi)]。ELM的数学模型可以表示为：

Hβ=T

(4)

其中，H=[h(x1),h(x2),…,h(xN)]T为所有样本对应的隐藏层输出矩阵；β为待求解的输出层权重矩阵；T=[t1,t2,…,tN]为样本类标所对应的期望输出矩阵。

利用最小二乘法，β可通过下式进行求解：

(5)

其中，H为H的Moore-Penrose广义逆，可以保证所求得解为式4的最小范数最小二乘解。因此，极限学习机可通过一步计算得到，无需迭代，使得训练时间大幅缩短。

也可从优化角度来描述和求解ELM。为最小化训练误差且同时提升模型的泛化能力，需同时对‖Hβ-T‖2和‖β‖2做最小化处理，故该问题可描述为如下形式：

(6)

其中，ξi=[ξi,1,ξi,2,…,ξi,m]表示样本xi在所有输出节点上对应的训练误差向量；C表示惩罚因子，用于调控模型训练准确性与泛化性二者之间的均衡关系。

式6可通过求解得到，给定一个具体样例x，其对应的实际输出向量可由下式求得：

(7)

其中，f(x)=[f1(x),f2(x),…,fm(x)]表示样例x的实际输出向量，而该样例的预测类标为向量f(x)中元素最大的值对应的类别。

2 文中算法

2.1 极限学习机的多标记应用

ELM的网络结构不仅适用于单标记学习，也同样可用于多标记学习[9]。在多标记学习中，式6、式7依然有效，输出节点个数不再代表类别的个数，而是多标记数据类标的个数，即m个输出节点代表每个样例关联m个标记。

标记判别时，单标记中，单个样例仅关联一个标记，仅需求出输出向量f(x)中元素最大值的对应标记即可；而对于多标记问题，单个样本可能关联多个标记，此时，需要设定一个阈值函数th(x),并通过下式预测类标：

(8)

因此，阈值函数th(x)的确定成为了解决该问题的关键。

2.2 阈值自适应选取策略

类别不平衡问题中常用的阈值选择方式有[14]：根据经验来设定阈值[15]，即th(x)等于一个常数θ；采用优化技术来确定阈值[16]，即th(x)等于一个向量[θ1,θ2,…,θm]。对于多标记分类问题，类标空间维度往往较高，因而阈值选择也会更加困难，故简单的由经验来设定阈值的方式通常不会取得理想的分类效果，所以文中关注如何通过优化技术来设定最优阈值，则问题就转变成了一个多变量的最优化问题。

首先选取不平衡问题的常用性能度量指标Macro F-measure(Macro-F)为优化目标。首先基于统计量求得在各个类标上的分类性能，然后再将所有类上的测度均值作为最终结果。计算公式如下：

(9)

其中，|y|表示类标数。

(10)

(11)

(12)

其中，TP表示真正类；FP表示假正类；TN表示真负类；FN表示假负类。

其次选用PSO粒子群优化算法[17-18]。在PSO中，每个粒子有适应性，能够与环境及其他粒子进行交流，并根据交流的过程学习来改变自己的结构与行为，以此达到最优。在PSO算法优化过程中，每个粒子通过学习其自身经验(pbest)和种群其他成员的经验(gbest)，动态改变各自的位置和速度。其每轮的更新方式如下：

(13)

2.3 MLTA-ELM算法流程

综上所述，下面给出了MLTA-ELM算法的整体流程。

输入：多标记训练样本S:{(xi,Yi)|i=1,2,…,n}，隐层节点数L，惩罚因子C；

输出：所训练的多标记分类器MLTA-ELM。

步骤1：训练多标记的ELM分类器。

(1)根据输入节点数，隐层节点数L，惩罚因子C与多标记类别个数，随机生成网络模型的隐藏层权重和偏置，设置激活函数为sigmoid函数；

(2)在训练集S上根据式6训练ELM分类器M；

(3)获得训练集S在模型M上的实值输出的矩阵f(x)。

步骤2：最优阈值组合选取[θ1,θ2,…,θm]。

(1)种群初始化，包括初始位置、速度等；

(2)计算每个微粒的适应度；

(3)计算粒子所经历的最好位置pbest，并计算群体中所有粒子经历的最好位置；

(4)根据式13进行速度和位置更新；

(5)反复执行步骤2～4，直到达到最大进化迭代次数；

(6)最大适应度对应种群中的位置，即所求最优阈值组合。

步骤3：标记预测。

对于一个样例x，首先通过步骤1获得输出矩阵f(x),将其与最优阈值组合[θ1,θ2,…,θm]根据式8进行比较，获得判别标记。

3 实验与结果分析

3.1 数据集与实验设置

实验主要在12个基准的多标记数据集上完成，这些数据集涵盖了文本、音频、生物等不同场景。各数据集具有不同的样本数、类标数、标记密度及不平衡比率。有关这些数据集的具体信息见表1。

硬件环境：Intel酷睿i7-555U处理器，CPU主频3.1 GHz，内存8 GB，硬盘1 TB，操作系统为Windows 8.1；编程环境为Matlab2015b。

为验证提出算法的有效性与优越性，将其与几种经典的多标记不平衡分类算法进行实验比较，比较算法包括COCOA[7]、ML-SMOTE[5]、ML-ROS[6]、ML-RUS[6]以及标准ELM等。各类算法所特有的参数均按照代码中的原始最优设置而设定。COCOA算法中特有的参数K，ML-ROS、ML-RUS中的特有参数P，根据对应参考文献分别设置如下：K=min(q-1,10)，P=10%。在标准的ELM算法中，各类标对应的阈值均为缺省值0。同时，为了保证实验的公正性，除COCOA采用对应文献自带的分类器外，其他算法均采用ELM作为基分类器。ELM算法中的两个参数，隐层节点数L及惩罚因子C，则通过内部五折交叉验证的grid search方法进行选取，选取范围为：L∈{50,100,…,1 000}，C∈{21,22,…,220}。此外，考虑到实验中各种算法均存在一定的随机性，故实验结果以50次随机5折交叉验证所计算得到的均值形式给出。性能测度指标分别采用Macro F-measure (Macro-F)及Micro F-measure (Micro-F)。

3.2 结果与讨论

表2及表3分别给出了各算法在各个数据集上的Macro-F及Micro-F性能测度值。

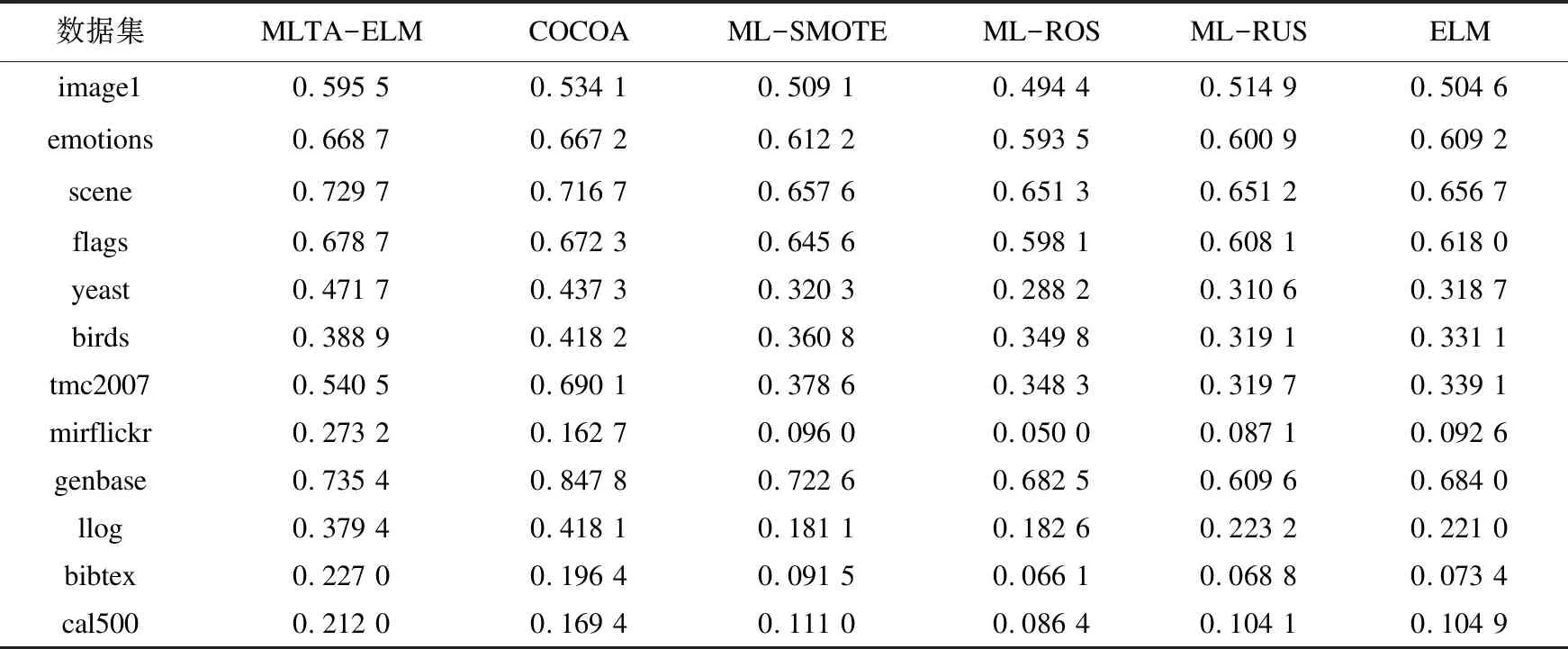
表2 各算法在各数据集上的Macro-F结果

表3 各算法在各数据集上的Micro-F结果

从这些实验结果中，可以得出如下结论：

(1)从两种性能测度的结果来看，无论采用采样技术、集成学习技术还是文中采用的阈值技术，均可或多或少地缓解样本不平衡分布对分类器性能所产生的负面影响。这一结论主要体现在各类算法与基准ELM分类器的结果比较上。

(2)在几乎全部数据集上，MLTA-ELM与COCOA算法均显著优于ML-SMOTE、ML-ROS及ML-RUS算法。究其原因，前两种算法属于算法适应型，其在算法模型上进行了针对性的改动以适应多标记数据中的不平衡现象，而后三种算法则采用了采样的策略，是立足于通过调整数据分布以弥补数据的不平衡分布，具有一定的随机性，同时也容易出现过拟合与欠拟合的现象。

(3)相较于ML-ROS与ML-RUS，ML-SMOTE算法在绝大数据集上都有不同程度的性能提升，这是因为该算法不再简单地对少数类样本进行复制，而是通过一定策略生成大量新样本的方式来谋求训练样本集类分布的平衡，因此采样结果更具泛化性。这一结论也可通过比较ML-ROS、ML-RUS与基准ELM算法的结果而得出：在不平衡比率较大的数据集上，ROS与RUS算法的性能往往低于基准ELM算法，而ML-SMOTE相较于基准ELM算法则通常会有一定的性能提升，这也再次证明了对多标记数据进行随机采样往往会造成过适应，而ML-SMOTE算法则可有效规避该问题。

(4)与除COCOA算法外的其他多标记不平衡学习算法相比，MLTA-ELM算法在性能上均有较大幅度的提升。具体而言，在两个性能测度上，MLTA-ELM算法分别在8个和6个数据集上获得了最优的性能，充分说明了MLTA-ELM算法能够根据不同的数据分布自适应地选择最优阈值组合。至于为何其在Marco-F测度上的效果要更优，相信原因在于PSO是以该测度为寻优目标相关。

(5)相比于COCOA算法，文中算法并未体现出显著的优势。究其原因，不难发现：COCOA算法利用了标记间的相关性信息；COCOA算法采用了集成学习模式来提升分类模型的泛化性与分类性能，而这也是文中算法所欠缺的。当然，在实验中也发现，文中算法的时间开销往往远小于COCOA算法，尤其在类标规模较大的数据集上，这一优势通常会体现得更加明显。

3.3 参数分析

最后，分析参数对模型的重要程度。选取了标记小于10的数据集scene和标记大于100的数据集cal500。通过实验获取了不同参数L、C时对应的模型指标Macro-F。

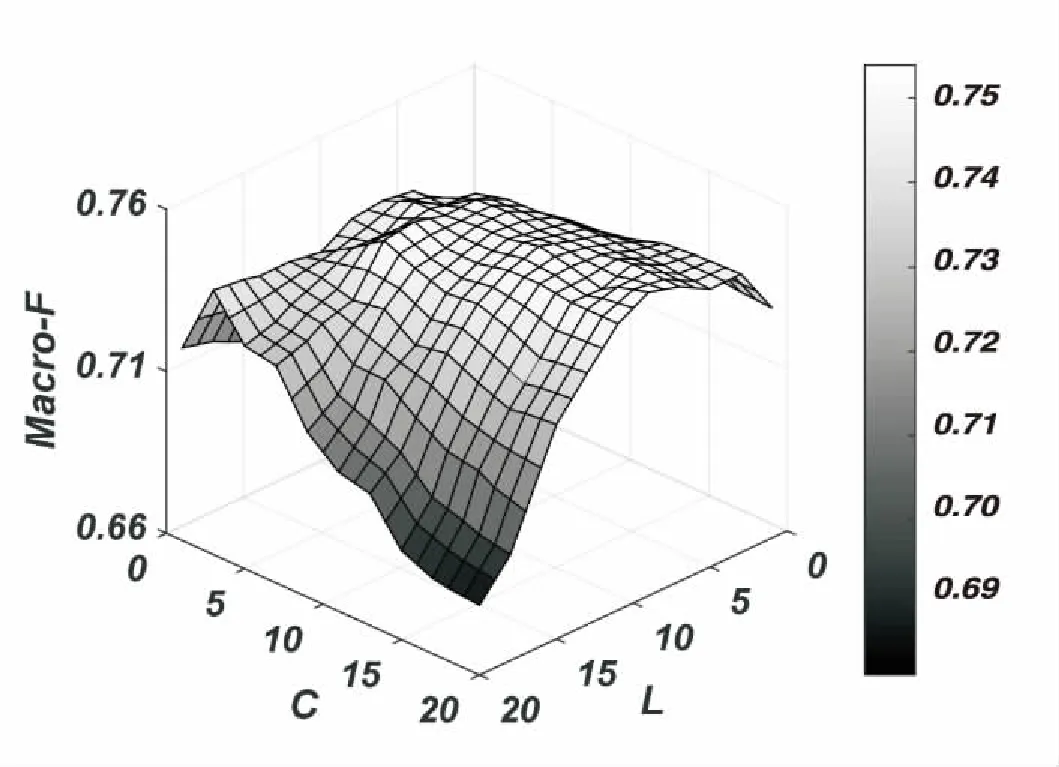
(a)scene

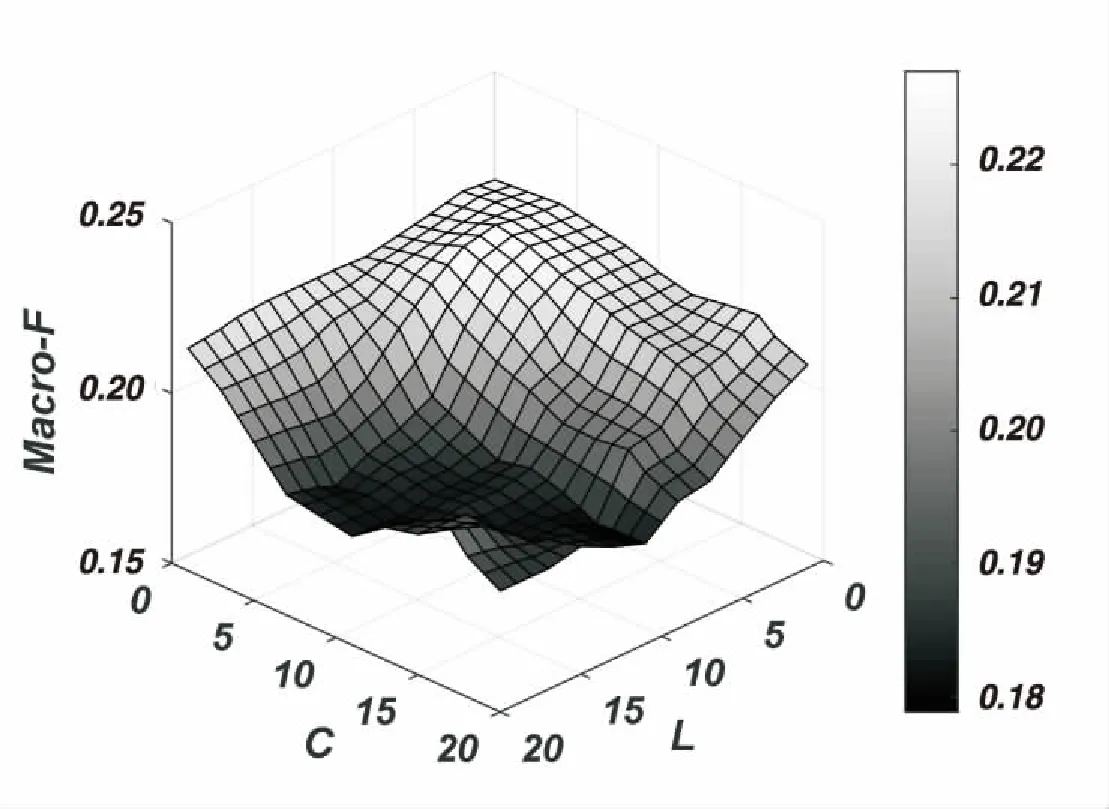
(b)cal500 图1 不同L与C下的Macro-F

由图1可见，在不同参数L、C下，其结果会随着参数的变化而较为平滑地上升或下降。可以看出，两个数据集中，在选定的参数范围内，均存在最小值与最大值，且最大值不处于边缘状态，也就是说，该参数范围是包含了最大值范畴的，也证明了该参数范围是有效的。

此外，实验分析了粒子群算法迭代次数与标记个数的关系，理论上，标记数的大小，表明标记空间维度的大小，在高维空间中搜索的范围会更大，需要的迭代次数也越多。通过图2可以看出，在scene与cal500上的收敛迭代次数分别为20多次与60多次。由此可以得出，标记数越大，其迭代次数会越大。

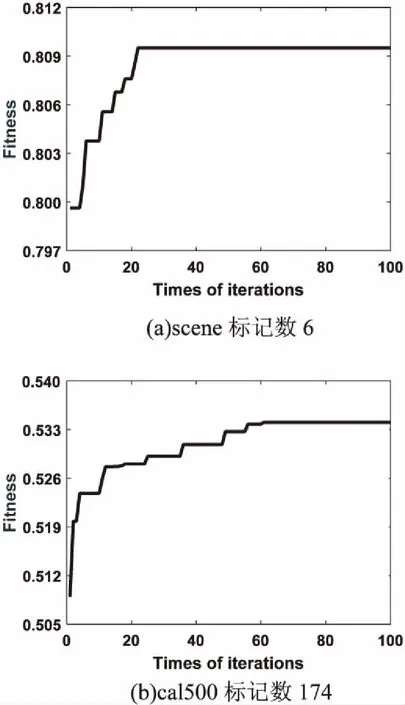
图2 粒子群算法100次迭代过程的适应度变化曲线

4 结束语

针对多标记数据中广泛存在的类别不平衡问题，提出了一种基于粒子群的多标记自适应阈值极限学习机(MLTA-ELM)算法。该算法以Macro F-measure为优化目标，将多标记阈值选择问题转化为一个多维连续空间的优化问题，并通过粒子群优化算法进行求解，以自适应地构建较优的多标记分类模型。在12个多标记数据集上的实验结果表明，与诸多同类算法相比，该算法极大地提升了多标记分类的性能，可以满足各种实际应用的需求。但该算法未考虑类标间的相关性，若将该信息融合进分类模型，相信可以进一步提升分类性能；由于引入了随机优化过程，故该算法的时间复杂度仍然较高。对于这些问题，该算法还有待进一步的改进。