多功能捣炉车工作装置优化设计
2019-04-18徐家军刘昌盛
徐家军 刘昌盛 徐 波
(山河智能装备股份有限公司 湖南长沙410100)
1 前言
多功能捣炉车是目前大中型硅铁还原炉及其他同类型电炉生产铁合金时用作加料、推料和捣炉的常用设备。其作用是既能加料,又能借助可更换的工具使电炉炉内布料均匀,扩大反应区,并消除悬料、捣碎熔渣,减少结壳和料面喷火,达到炉况最佳[1]。山河智能研发的自由行走式多功能捣炉车具有加料、推料及捣炉的功能,适用于容量为10000~40000KVA的大型电炉。其主要特征是:采用卷筒电缆供电;全部动作均为液压驱动;三轮行走;工作部分为四连杆机构,其前臂既可上下摆动,又可前后伸缩;装料箱卸料为刮板推出方式,做捣炉用时可迅速将装料箱换成捣料杆;整机由一人操纵。
随着有限元分析技术的发展和应用的普及,越来越多的人认识到,有限元分析在缩短产品研发周期、提高产品可靠性和降低生产成本方面是一种非常有效的方法。相对于其他方法,有限元法比较容易计算结构任意一点处的应力、变形等[2]。本文对多功能捣炉车的工作装置进行有限元分析,找出了其结构强度的薄弱环节和工作装置发生故障的原因。为后续工作装置的优化设计提供理论依据。
2 工作装置有限元分析
2.1 有限元法基本原理
通过将原有模型分为简单形状的单元,将给定问题离散化。单元和周围节点之间的关系可以描述为:[k]e{u}e={f}e。单元刚度矩阵[k]e来源于几何外形、材料属性和单元属性;单元载荷向量{f}e描述作用于单元上的载荷;位移向量{u}e在方程中为未知量, 描述了在外部载荷作用下节点是如何运动的。接下来单元刚度矩阵组成总刚度矩阵, 载荷组成了总载荷向量。 得到整个结构的矩阵方程:[k]{u}={f}。下一步为模型加载边界条件(约束模型),从数学上就是移除总矩阵方程中与约束自由度相对应的行和列。最后求解总矩阵方程得到未知的节点位移,通过节点位移再计算单元应变和应力[3]。
2.2 工作装置简介
工作机构为一个带操作臂的四连杆机构,结构如图1所示。主要有3种功能:操作臂摆动,由两个摆动油缸控制,用以调节操作臂的摆动角度和捣炉;操作臂前后伸缩,由一个伸臂油缸控制,以实现工作时将操作臂伸出,不工作时将操作臂缩回的要求;推刮卸料,由一个带导向套筒推料油缸控制,用以实现装料箱卸料。为避免因操作意外导致与炉内电极接触而使机身带电,四连杆机构与机架之间的各联结点均采取绝缘措施,捣炉作业示意图见图2。

图1 工作装置三维模型

图2 捣炉作业示意图
2.3 有限元建模
所有零部件板材均采用二维壳体单元模拟,而液压缸用杆单元、轴用粱单元、铰接点用MPC单元来模拟。弹性模量E=2.1e+5MPa,泊松比V=0.3,密度ρ=7.85g/cm3。
首先处理几何模型,用CAD软件对三维模型抽中面,然后通过拉升、裁剪等命令对面模进行修补,完成工作装置面模后,保存为Step中间格式文件。本文采用HyperMesh打开前面保存的Step格式文件,对其划分网格和赋属性,二维网格单位选用TRIA3和QUAD4,结果见图3,然后保存为bdf格式文件。

图3 网格划分
在MSC.Patran中导入前面保存的bdf格式文件后,需对工作装置有限元模型进一步完善。最后施加约束和载荷:油缸铰接处、摇臂底部与平台的铰接处施加铰接约束;本文分析的多功能捣炉车最大输出扭矩为56kNm,最大捣炉力为80kN,在工作装置装上3.5米长的捣炉杆后,捣炉杆末端的等效力为15kN,本文用RBE2单元模拟捣炉杆。
2.4 有限元分析结果
通过MSC.Nastran对有限元模型进行求解,得出图4~图8所示应力云图。工作装置材料为Q345B,安全系数n取1.5,许用应力[σ]=345/1.5=230MPa。从应力云图可以看到:工作装置最大变量为6.14mm,最大应力为378MPa。其中摇臂最大应力为97.7MPa,满足强度要求;后操作臂最大应力342MPa,大于许用应力,不满足强度要求;前操作臂最大应力378MPa,大于许用应力,不满足强度要求。
由分析得出,现有工作装置结构中,前后操作臂几处应力集中部位的应力超出了许用应力,需要局部改进提高强度。而摇臂的应力都处于100MPa以下,应力还有比较大的余量,可以考虑减重处理,节省材料。

图4 工作装置应力云图

图5 摇臂应力云图

图6 后操作臂应力云图
3 优化设计前后有限元分析对比
3.1 结构优化方案
从有限元分析结果可知,工作装置应力只在几处应力集中的地方超出了许用应力,其余都在允许范围内,特别是摇臂的应力余量还较大。所以不考虑增加材料厚度提高强度,而从增加筋板局部提高强度方面优化结构。在前后操作臂法兰接口处、臂支撑横管和梯形板处加筋板,对摇臂开多个减重孔,优化后的三维模型如图8所示。
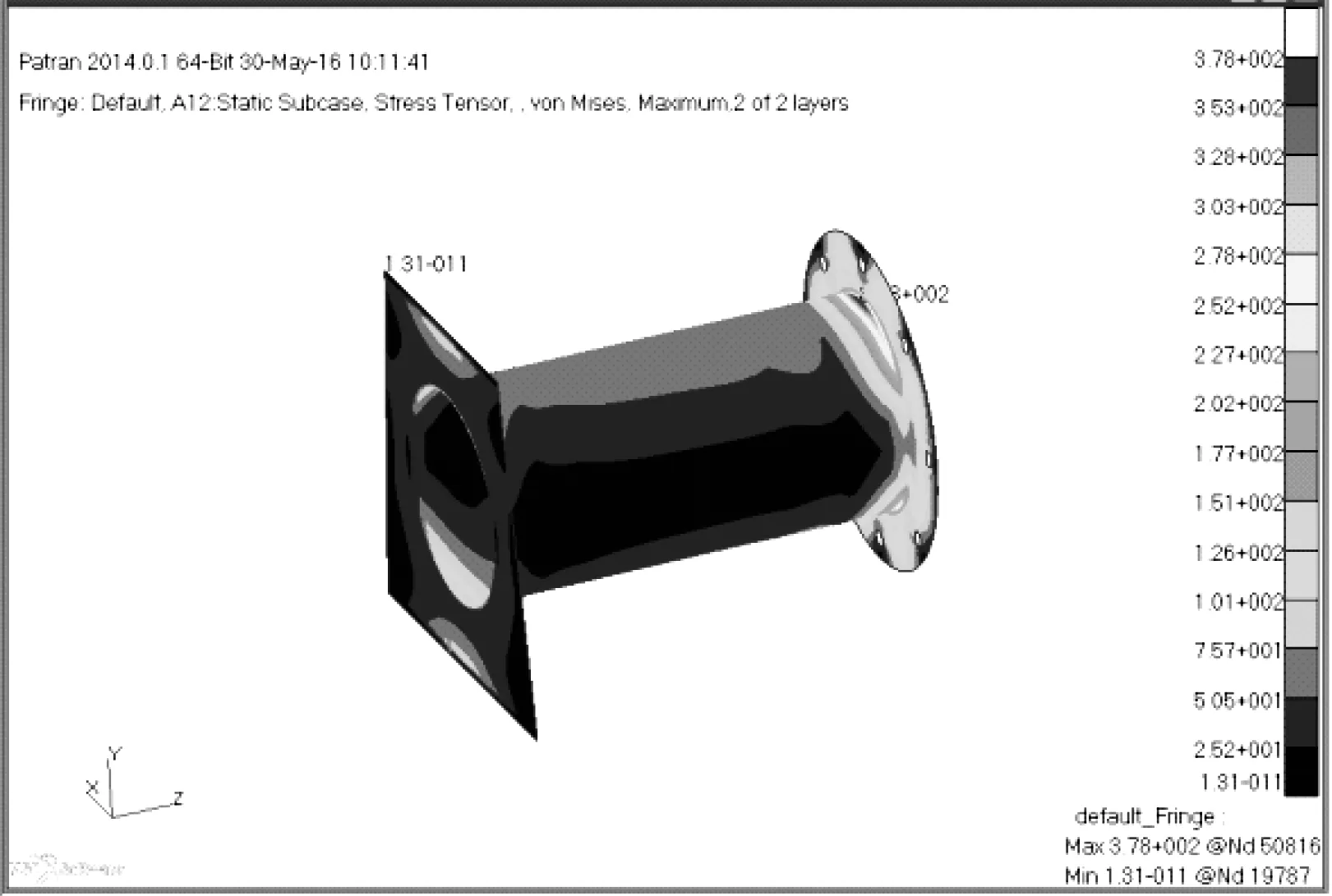
图7 前操作臂应力云图

图8 结构优化后三维模型
3.2 优化设计后有限元分析结果
优化后结构分析结果 :工作装置最大变量为4.82mm,最大应力为226MPa。从分析结果可以说明工作装置优化设计方案是可行的。
3.3 优化前后结构与有限元分析结果对比
工作装置各部件优化前后的结构对比和有限元分析结果对比见图9和表1。
4 试验测试与计算结果对比分析
试验测试应力设备为CL型应力应变专用测量仪。首先在发生开裂故障位置和有限元分析得出的一些危险点位置进行标记,在工作装置上选取六个测试点并对选定测试点进行打磨,到表面光滑平整为止。在受力方向明确的位置贴应变片,在受力方向复杂的位置贴应变花。测试结果取测试曲线的最大值,采样频率200Hz。试验实测结果与有限元计算结果对照表见表3,由对照结果可看出,各点的误差均较小,误差在可接受范围内,出现误差的主要原因在于:模型的简化和试验时工作装置的状况与计算工况存在差异。通过试验实测结果和有限元分析结果分析对比说明力学模型及用板壳单元建立的有限元模型是可行的,其分析结果是合理可靠的。

图9 优化前后结构对比
5 摇臂屈曲分析
因对摇臂进行了轻量化设计,为了安全起见,还需对其优化后的机构进行屈曲分析。在载荷作用下,结构发生变形,并在结构内部产生内载荷。平衡方程[K]{U}={P}写为变形状态为:
([K]+[KD]{U*})={P}
(1)
矩阵[KD]是微分刚度矩阵。 微分刚度矩阵是包含应变-位移关系的高阶项(非线性项)产生的刚度。微分刚度矩阵与结构内载荷成比例。可以将方程(1)写为:
([K]+λ[KD]){U*}=λ{P}
(2)

表1 优化前后应力值对比

表2 测试值与计算值对照表
对方程(2)两端进行求导,对结构的平衡位置加以微小的扰动:
([K]+λ[KD]){U*}=λ{dP}
(3)
在临界屈曲载荷下,参考构型和微小扰动(屈曲)构型都可能处于平衡位置。因此,此时发生一定的位移{dU*},载荷不会改变。这样将屈曲稳态转化为特征值问题:
([K]+λ[KD]){dU*}=0
(4)
([K]+λ[KD]){φ}=0
(5)
对于每个特征值λi,都有一个与之对应的特有的特征向量{φi}表示屈曲形态。则临界屈曲载荷为{P}cri=λi{P}。通常只关心最低的特征值λ1, 这是因为它与结构的最低屈曲载荷相关。特征值λ也称为屈曲载荷因子。如果λ≤1.0,则说明结构已经发生屈曲[2]。对摇臂进行屈曲分析,求解出前5阶屈曲特征值。其中第一阶屈曲特征值λ=33.068(图10所示),在前5阶屈曲特征值中最小,但远大于1,所以摇臂的稳定性是满足要求的。

图10 屈曲分析结果
6 结论
1)对现有多功能捣炉车工作装置结构进行有限元分析,找出了其结构强度的薄弱环节;
2)优化设计了工作装置的结构,优化后的结构应力最大226MPa,最大变形4.82mm,摇臂的屈曲载荷因子λ=33.068,满足强度、刚度和稳定性的要求,对应力余量大的部位开减重孔,大大节约了材料成本;用试验验证了有限元分析结果的合理可靠性。
