行波管最优声场的获取方法研究

佟昊阳

（第七一五研究所，杭州，310023）

自美国 USRD（Underwater Sound Reference Dinision）提出并建立了用于换能器校准的行波管校准装置后，行波管的应用得到了水声界的广泛关注。经过多年的研究与发展，行波管的用途不再仅限于换能器校准。在模拟深海环境条件下，测量材料回声降低、插入损失和吸声系数，大面积水声构件的样品测试，有源吸声材料测试等诸多领域均有着广泛运用[1,2]。近年来，水声的研究领域逐渐向着深海发展，研究高压低温对水下设备的影响的需求越来越大。与高压水池相比，行波管有着体积小、实验频段低、易加压、易变温、声场分布简单等优点，因此行波管应用的研究变得更加重要和迫切。但它的缺点也十分明显。行波管利用主动消声技术，控制管体两端的发射换能器产生声波的幅值、相位差，实现声波在管中的单向传播。在调整发射换能器时，需要至少两只水听器，配合传递函数法检测管体内声场分布[3]。此外为了便于实验操作与样品放置，行波管通常是分为上、下两部分，每个部分需要各装两只水听器。这使得行波管装置的B类测量不确定度分量个数较多，进而影响测量的准确性。

在行波管测量中，行波场的理想程度是影响测量结果准确程度的主要因素之一。所有的行波管测量结果，都是建立在行波管内部分声场为行波场的前提之上得到的。保证行波管内产生的行波场足够理想是行波管准确测量的必要条件。在提高行波场理想程度的方法中，对行波场中水听器灵敏度的幅值、相位进行精确校准是最为直接有效的方法。目前对行波管中水听器灵敏度一致性校准的测量不确定度可以达到0.2 dB[4]，但由于传递函数法的特殊性质，只要水听器灵敏度校准误差存在，在测量声管中声场分布时就会在特殊频率区间产生极大的测量误差，使得行波管中行波场的理想程度达不到测量要求，进一步降低行波管的测量不确定度就需要研究新的方法降低对声管中声场的测量误差。

1 行波场生成原理

行波管内行波场生成的原理如图1所示。在行波管的两端，各安装一只发射换能器，其中一只为主换能器、另一只为辅助换能器。在需要形成行波场的部位安装1#、2#两只水听器，水听器位置记为x1、x2，一般行波管内水听器为同型号同批次水听器。为了计算方便，默认行波管水听器灵敏度一致，记为M。主发射换能器发射频率为行波管截止频率以下的单频信号，使得行波管内声波为平面波。利用两只水听器测得的开路电压U1、U2得到水听器所在位置的压强P1、P2。

图1 行波场生成原理示意图

将从主发射器向辅助发射器方向传播的声波记为入射波Pin、另一个方向传播的声波记为反射波Pre，Pin与Pre的测量值均为复数。可以利用传递函数法得到如下关系式：

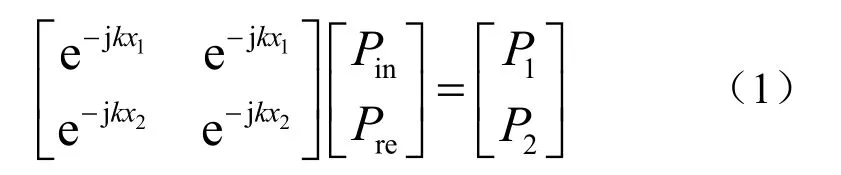
而后调整辅助发射换能器的幅值、相位，使反射波的幅值为0，此时：

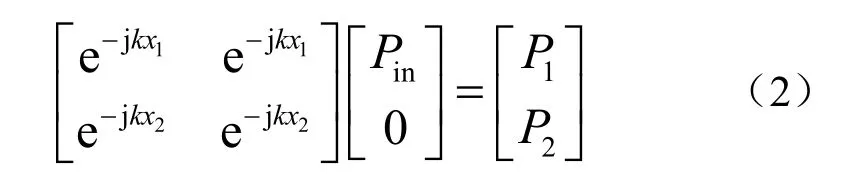
得到行波场形成后，P1、P2之间应满足的关系式：

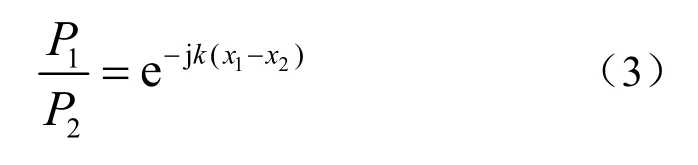
2 水听器位置对行波场判定的影响

在实际测量中，1#、2#水听器位置处的声压是通过水听器两端的开路电压U1、U2与水听器灵敏度M推算得到的。因此在实际测量中，判断行波场形成依据：

式中，P1、P2表示1#、2#水听器处声压的测量值，水听器的灵敏度校准是有误差的，设水听器的校准误差为ε1、ε2。此时行波管中1#、2#水听器处声压的实际比值为：

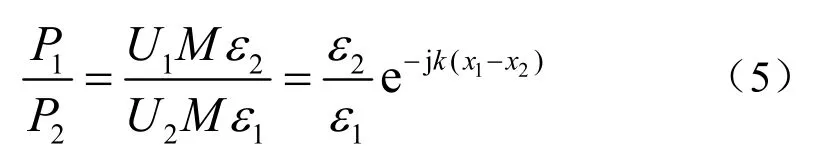
通过计算可知，此时Pin、Pre比值的绝对值|R|为：

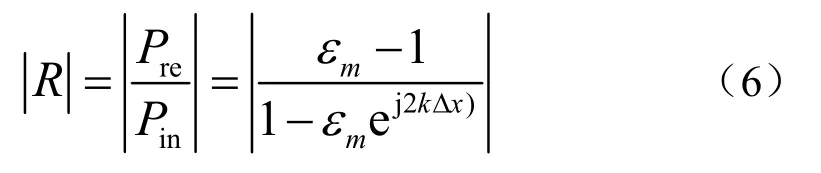
式（6）中，|R|代表了测量行波管内部声场时的测量误差，|R|的值越小对行波管中的声场测量结果越准确，以此为依据建立的行波场越理想。而εm为ε1、ε2的比值，表示1#与2#水听器的一致性，εm为复数：

式中，εM为εm的分贝形式。当εM的值为0时，即1#、2#水听器灵敏度完全一致时，|R|的值为0，即当前管中声场为理想状态下的行波场；而当εM的值不为0时，可以看出|R|的值受到kΔx的影响。当εM=0.2时，即水听器灵敏度差异为0.2 dB时，|R|关于kΔx的函数图像如图2所示，可得|R|关于kΔx的函数是周期为π的周期函数。由式（6）可知：

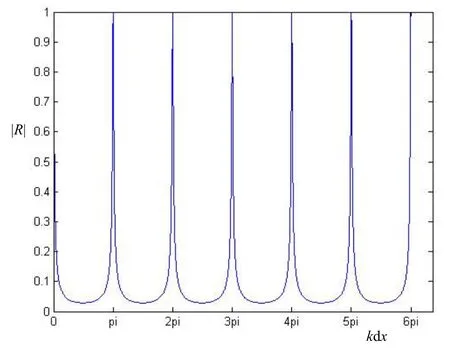
图2 行波管中声场的测量误差|R|关于kΔx的函数图像

在实际实验中，由于测量不确定度的存在，水听器的灵敏度差异一直存在，所以对于行波管中任意一组水听器，总会有频率区间使得行波管内行波场的理想程度无法达到实验条件要求。水听器组灵敏度的一致性越好，该区间越小。因此需要对水听器位置进行讨论，对不同频率点选用适合的水听器测量，得到更为准确的测量结果。

3 模拟分析

由于传递函数的特殊性质，在实际实验的过程中，无法从数据处理的角度消除水听器灵敏度一致性对行波场的影响。行波管中声场测量误差|R|是关于kΔx的周期函数，因此可以选用不同间距的水听器组合来形成行波场，将误差小的频率区间进行组合，最后达到全频率测量结果准确度提高的效果。

3.1 实验装置介绍

进行模拟的行波管管体内径 Φ208 mm、外径Φ416 mm、长5 m，垂直于水平面放置的不锈钢厚壁圆柱声管，声管内部充满纯净水。行波管内水听器安放与装置连接如图3所示。整套实验装置由管体、发射器、水听器、电子测量仪器、辅助设备及控制系统和校准软件组成。声管两端分别装有主发射器和次发射器；行波管中共有8只水听器固定在管壁上，其传感部分位于声管中心轴上，以声管中央为中心上下各4只对称放置；温度和压力传感器也安装于行波管中，可对行波管中介质环境直接测量。电子测量仪器包括双路信号源、2只功率放大器、多路前放滤波系统、信号采集分析仪及计算机。辅助设备及控制系统包括压力、温度和液压机械控制，实现声管内部深海环境模拟和声管中部开合。

现规定声管中心轴为x轴，向上为正方向，声管开合处位置为x=0。下部声管布置1#、2#、3#和4#水听器，用以通过传递函数法计算下部声管的声压分布；上部声管布置 5#、6#、7#和 8#水听器，用来辅助在上半部分声管形成行波场。以xm表示行波管中m#水听器位置，8只水听器的位置如表1所示。

图3 实验装置示意图

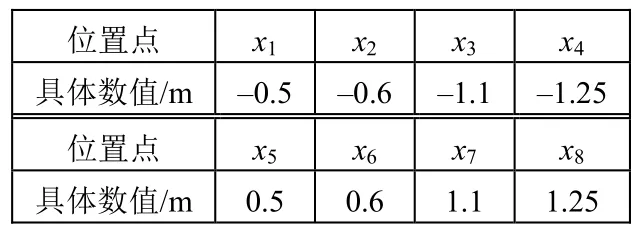
表1 行波管中水听器位置

3.2 模拟计算结果

实验装置在形成行波场时，使用的是 5#、6#、7#和8#水听器，共有6种水听器组合。使用每一种组合建立行波场后行波场理想程度随频率f的变化如图4所示，各水听器组的灵敏度差异为0.2 dB。

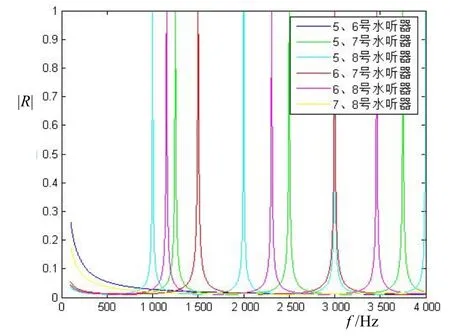
图4 不同水听器组合形成行波场的理想程度随频率f的变化

将每个频率点对应的行波场理想程度最高（即|R|值最小）的水听器组合提取并拼接起来后可以得到水听器经最佳选择后得到的最优结果，如图5表示。图5中行波场|R|最大值为0.038，全频段均符合测量要求。因此由模拟结果可知，通过选用适当的水听器组在不同频率段形成行波场就可以有效的提高行波场的理想程度，进而提高行波管的测量准确度。

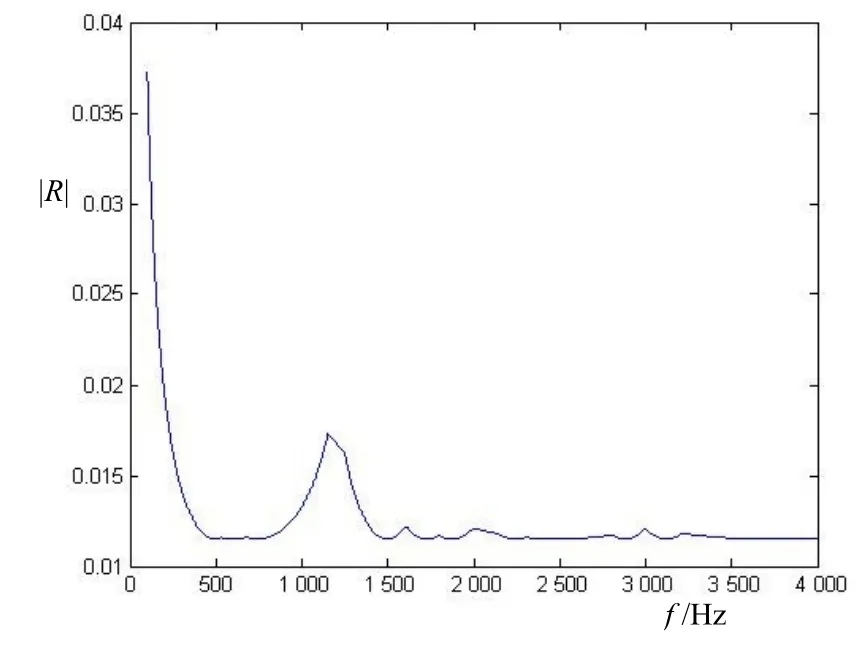
图5 水听器测量最优组合结果下行波场理想程度

4 实验验证

为了证明模拟结果的有效性，利用实验装置对6组水听器组合形成的行波场分别进行了测量。测量的频率范围为100～4 000 Hz，频率间隔为100 Hz。

首先为了证明水听器位置对行波管中行波场理想程度的影响，将任意一组（5#、8#）水听器的实验数据同模拟结果进行对比，如图6所示。

图6 水听器组合的行波场理论和实验结果对比

可以看到，实验数据在模拟结果的特殊频率点均有跳变，且整体趋势与模拟结果有着较好的吻合，可以证明模拟结果的可靠性。图7为6组水听器组合形成行波场的理想程度曲线，可以看到如果仅使用一组水听器形成行波场就会在特定频率区间得到较大的测量误差，选用水听器组不当也会增加测量误差。此时使用模拟结果中得到的水听器组合的选择方法形成行波场，得到的结果与6组水听器测量得到的最优结果进行对比，如图8所示。

可以看到，使用模拟中计算得到的水听器组组合的测量结果与实验结果中提取的最优结果相差不大且有效的避开了测量误差较大的区间，这说明使用适合的水听器组可以有效的提高行波场理想程度。

图7 各水听器组合形成行波场的理想程度曲线汇总

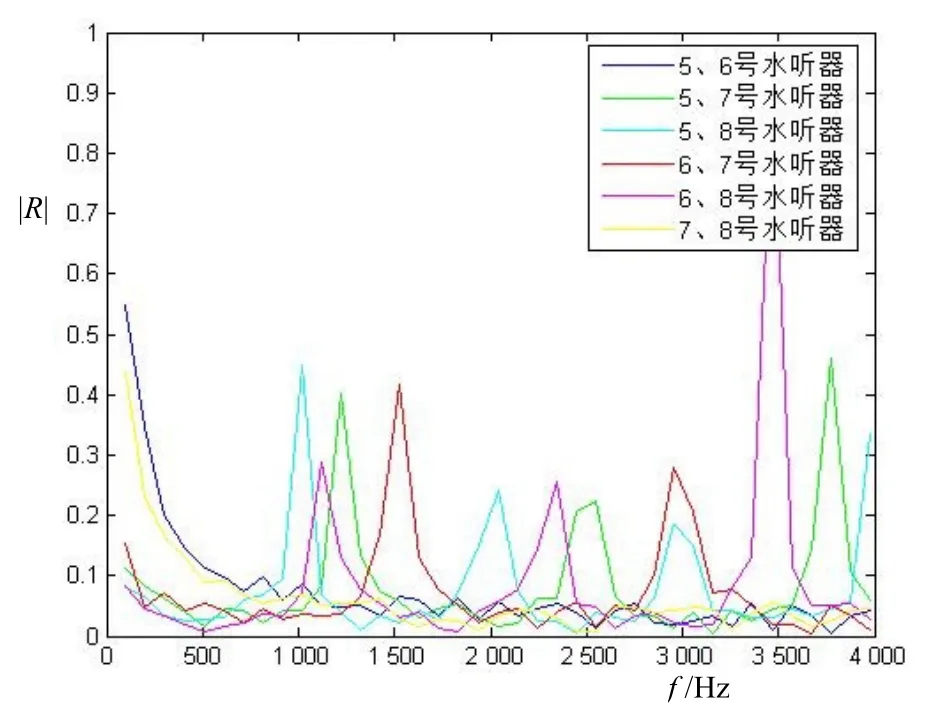
图8 实验最优结果与选择水听器组测量结果

5 结束语

行波管中行波场的建立是所有使用行波管进行实验测量的基础，本文通过理论计算和模拟指出了行波管中水听器位置对行波管中行波场建立的重要影响和获取行波管最优声场的方法，并通过了实验验证。

对于同一组距离固定的水听器，由于灵敏度校准误差存在的必然性，在一些频率点无法在行波管中形成符合测量要求的行波场。通过变更水听器组的方式得到更加理想的行波场，弥补了单纯提高水听器灵敏度校准来提升行波场理想程度的不足之处，提高了行波管中形成行波场的稳定性。有效的降低了行波管进行水听器校准、水声材料声参数等测量的不确定度，为行波管系统的测量精度提高提出了新的改进方向。

目前国内外对行波管中水听器位置的选择，仅是根据采样原理和避开行波场构建过程中声场的奇点两个方面进行考量，而本文经过理论推导得到了水听器间距、水听器灵敏度校准不确定度和行波管中行波场理想程度间的关系，可以进一步完善行波管设计中水听器位置选择的方案，得到更加稳定的行波管测量系统。