复合材料帽型加筋壁板轴压屈曲工程算法验证研究

杨俊清 王 俊 孟庆功 /

(上海飞机设计研究院，上海 201210)

0 引言

复合材料加筋壁板因其比模量大、比重小、比强度高，在民用飞机上使用比例日益增加。压缩载荷是机身壁板需要承受的一种主要载荷，受压屈曲失稳会引起结构失效和静强度破坏。蒙皮局部屈曲是飞机结构强度设计工程师首要考虑的结构安全问题，寻找探索一种相对准确而快速的复合材料加筋壁板蒙皮局部屈曲载荷计算方法具有实际意义和工程应用价值。

目前，国内外对复合材料加筋壁板的稳定性进行了一系列的探索和研究，主要集中在有限元数值分析方法和工程理论计算结合试验对比研究。孙中雷等[1]研究发现，在截面面积相等情况下，帽型加筋壁板比“T”型和“工”字型加筋壁板有更高的屈曲载荷。该结论与诸多研究相符合，也是某型飞机准备大量使用复合材料帽型加筋壁板的原因之一。童晓琳[2]使用能量变分半解析法研究得出，当铺层数大于等于八层时，复合材料层合板可以近似视为正交各向异性板，研究结论与相关教材[3]相符合，本文研究对象均大于九层，适用正交各向异性板屈曲理论。李蓝天等[4-8]用线性和非线性有限元法通过ABAQUS建立有限元模型，增加界面单元，设置失效准则，并结合物理力学试验，研究了复合材料加筋壁板的局部和整体屈曲失稳、后屈曲失效模式及破坏、包覆层对壁板破坏模式和承载能力的影响、加强筋参数对分析结果的影响等，获得相应的进展和结论。朱菊芬等[9]结合多年来承担国家基金委和航空航天部门的研究项目中取得的成果，开发了复合材料专用程序系统Composs来分析其诸多性能，取得了关键进展。韩庆等[10]通过开发子程序嵌入patran和ABAQUS求解复合材料加筋壁板的压缩后屈曲和剪切稳定性，与试验结果吻合较好。葛东云等[11-14]研究验证了有效宽度法、刚度等效修正法、分段法和渐进损伤法等研究了复合材料加筋壁板屈曲后屈曲性能。针对本文的试验件，笔者结合参考文献综合使用了多种工程理论方法，计算结果发现，对于帽型加筋壁板，当不考虑帽型底脚对筋间蒙皮厚度折算，使用四边固支的理想边界计算得出的结果与试验结果误差最小。本文中介绍的试验件及相关参数和类似结构在某大型飞机设计研发中大量使用，故该计算方法对型号设计具有参考意义和价值。

1 试验介绍

1.1 试验件介绍

复合材料帽型加筋平直壁板轴向压缩试验件如图1所示，由五根帽型长桁条以及两个金属框和复合材料蒙皮组成，其外形尺寸为1 002 mm×992 mm×150 mm。轴向压缩试验件包含5种铺层构型，蒙皮和桁条结构制造选用M21E/IMA，材料规范CMS-CP-309，单层厚度为0.184 mm；框结构制造选用2024-T42铝合金。材料和铺层相关信息如表2和表3所示，试验件矩阵如表1所示。

图1 “M”型轴向压缩试验件

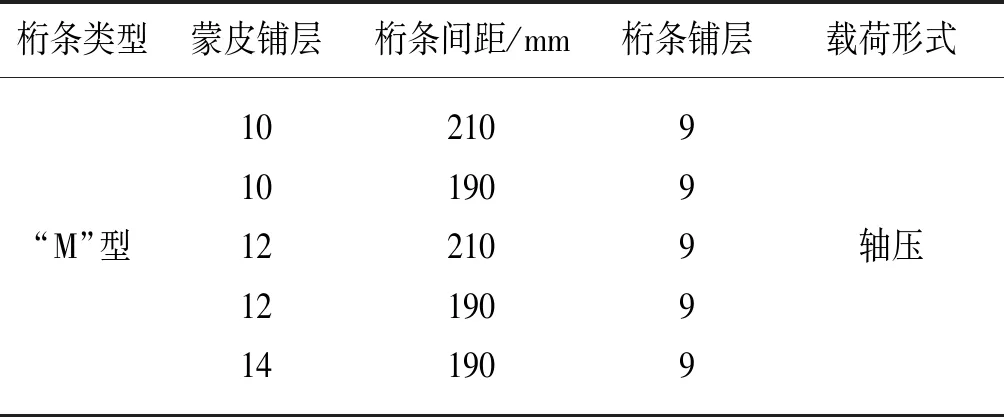
桁条类型蒙皮铺层桁条间距/mm桁条铺层载荷形式“M”型101012121421019021019019099999轴压

表2 材料属性

表3 长桁条和蒙皮铺层

1.2 试验支持及加载

轴向压缩试验在2 000 kN静力压缩试验机(ZWICK Z2000E)上进行。支持与加载方式如图2所示。试验时，将试验件垂直放置在试验机的支持平台上，上下框的左右两侧通过螺栓连接到搭板上，以限制框的扭转；搭板用刀口槽约束，模拟框的位置处的面外约束。调正压心后直接进行两端压缩加载，载荷合力作用点(试验机加载中心)与壁板截面的压缩中心一致。在低载荷下进行多次调试，当加筋板正面和反面的应变测量结果一致时，认为压缩中心已调准。

图2 试验件的支持和加载方式图

1.3 试验测量及结果

加筋壁板正反面贴上位移应变片以测量对应位置的应变，如图3所示。经数据记录及处理得到对应试验件轴向压缩屈曲载荷，其中一件的载荷-应变曲线如图4所示。

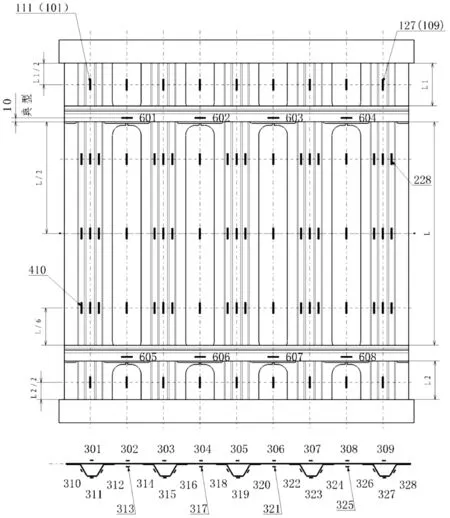
图3 “M”型的试验件的贴片图

2 局部屈曲载荷工程计算

通过试验发现，复合材料帽型加筋壁板在轴压载荷下首先发生局部蒙皮屈曲。对于帽型加筋桁条和考核区域局部蒙皮，其局部平板受轴向压缩作用如图5所示。其轴向压缩屈曲载荷计算按正交各向异性矩形层压板理论分析[15]。

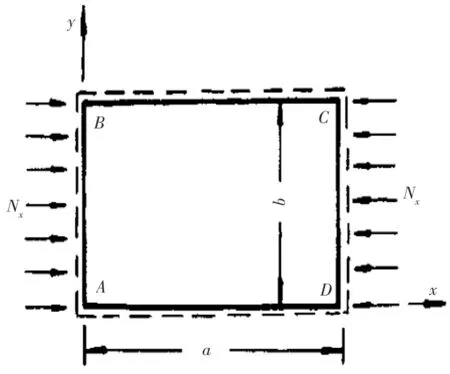
图5 轴压作用矩形平板

2.1 帽型桁条受压局部屈曲

帽型桁条的剖面如图6所示，2个帽底①、⑤与蒙皮粘接在一起，其边界支持较强，故不考虑局部失稳问题。只分析2个帽腰②、④和1个帽顶③，共3个板元的局部稳定性，得到各部分的许用应力，将最小值作为桁条的局部屈曲的许用值。帽型桁条的局部屈曲的许用值计算如下：

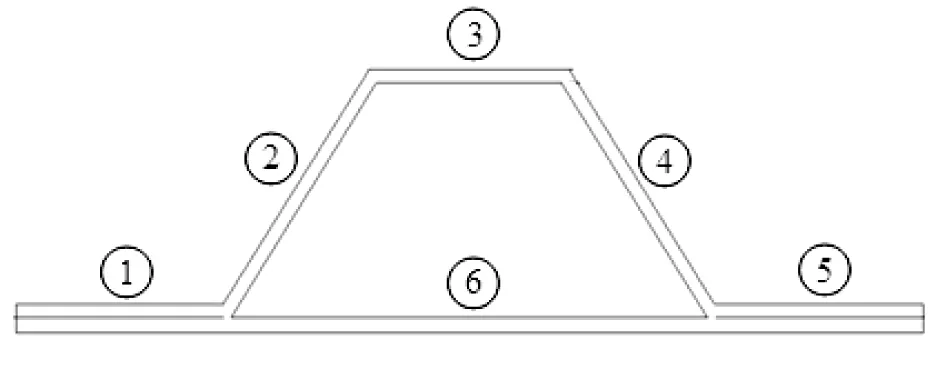
图6 帽型剖面示意图

②、③、④按两长边简支的长板处理，局部屈曲的许用载荷采用式(1)计算：

(1)

式中b为板元宽度。

取②、③、④3个板元的Nxcr的最小值作为桁条的局部屈曲的许用值。桁条各板元剖面刚度信息及受压局部屈曲计算结果见表4，帽腰板元②、④结果一样，表中只列出②。

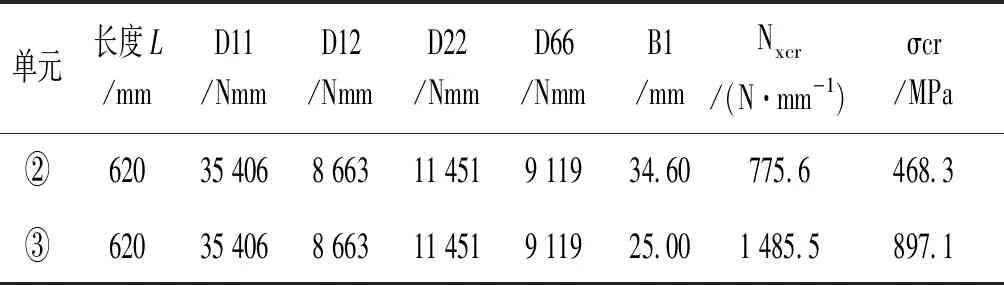
表4 长桁条刚度-屈曲的线力

2.2 受压蒙皮局部屈曲

蒙皮失稳分析的宽度选取如图7所示。

图7 板宽b的取法示意图

计算方法共有以下几类，如表5所示。

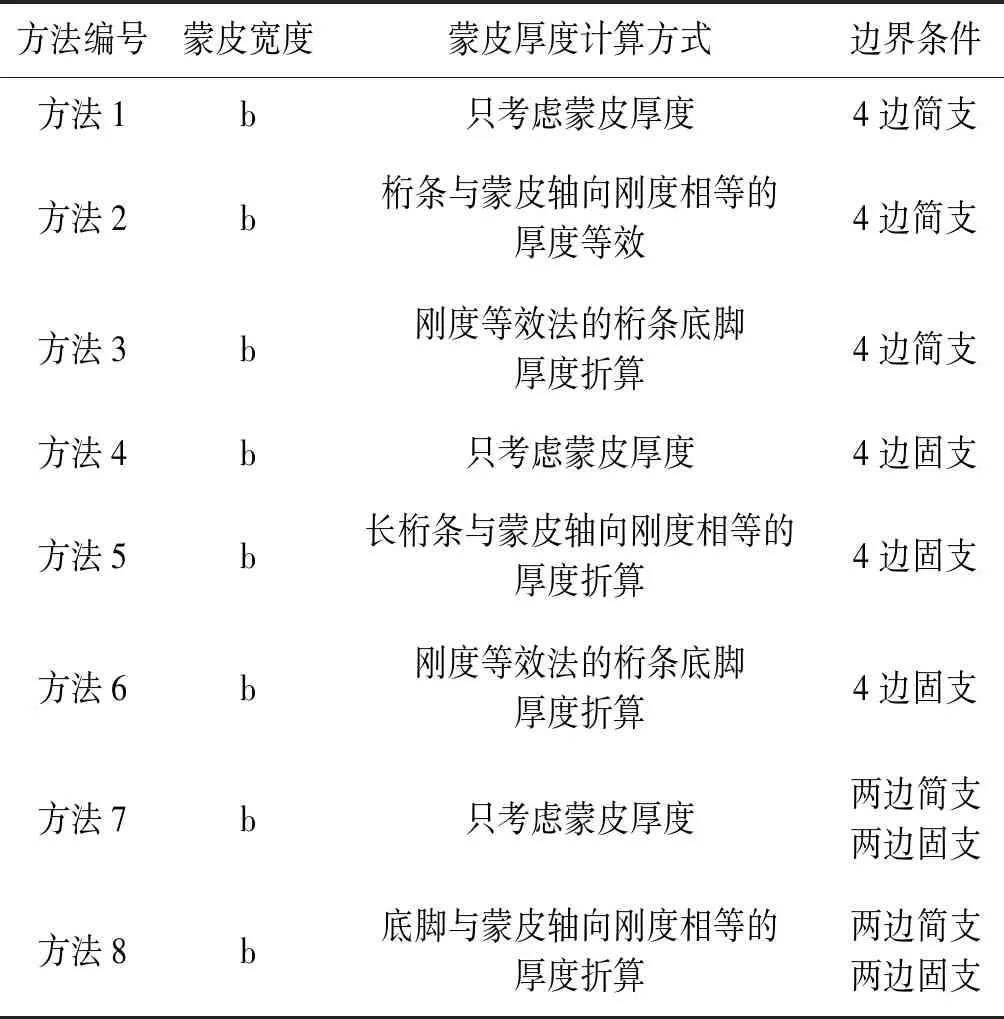
表5 屈曲载荷计算法

铺层数大于等于8层的复合材料层合板可以近似视为正交各向异性板，局部蒙皮考核区域屈曲载荷计算公式如下。

四边简支正交各向异性矩形层压平板轴压屈曲载荷公式：

(2)

四边固支正交各向异性矩形层压平板轴压屈曲载荷公式：

(3)

两压缩边固支两长边简支正交各向异性矩形层压平板屈曲公式：

(4)

式中，m为壁板受载的方向屈曲半波数，取m=1,2,3，…，计算相应的一组Nx，其中最小的即为板的屈曲载荷Nxcr。

考虑帽型长桁条帽底的支持时，考虑长桁条铺层和蒙皮铺层的轴向弹性模量相同时，采用式(5)和(7)修正帽型长桁条的底脚对加筋桁条间蒙皮厚度的贡献；考虑长桁条与蒙皮轴向弹性模量不同时，采用式(6)和(7)修正帽型长桁条底脚对加筋桁条间蒙皮厚度的贡献，即刚度等效修正法。

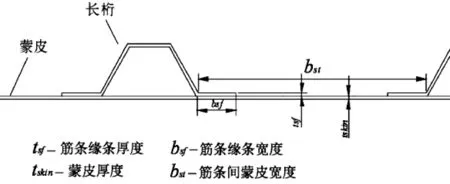
图8 帽型加筋壁板结构示意图

tavg=(2btst+btskin)/b

(5)

tavg=tskin+2bsftsfEsf/Eskinb

(6)

tply,skin=tavg/n

(7)

式中：a为框间距；n为蒙皮铺层层数；b为长桁条间距，同图中bst；bsf长桁条的板元的宽度；tsf为长桁条板元的厚度；tskin为蒙皮厚度。

蒙皮厚度与抗弯刚度D矩阵的计算关系可由经典层合板的理论计算[16]。将各个情况计算结果汇总如表6、7、8所示。因方法3和方法6计算的屈曲载荷数值均大于对应的方法2和方法5计算结果，故两边简支两边固支公式没有计算考虑刚度等效时的结果。表中误差百分比大于零，表示计算值比试验值保守；误差百分比小于零，表示计算值比试验值大。

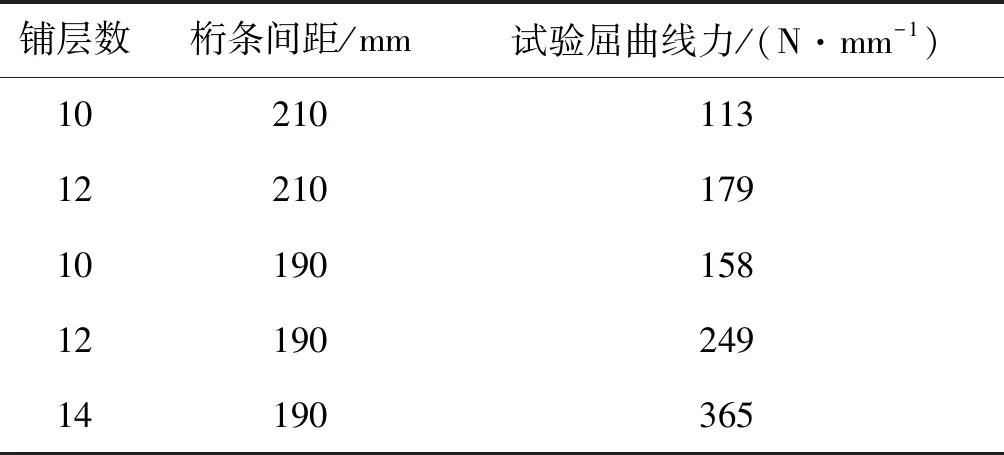
表6 试验计算屈曲线力值

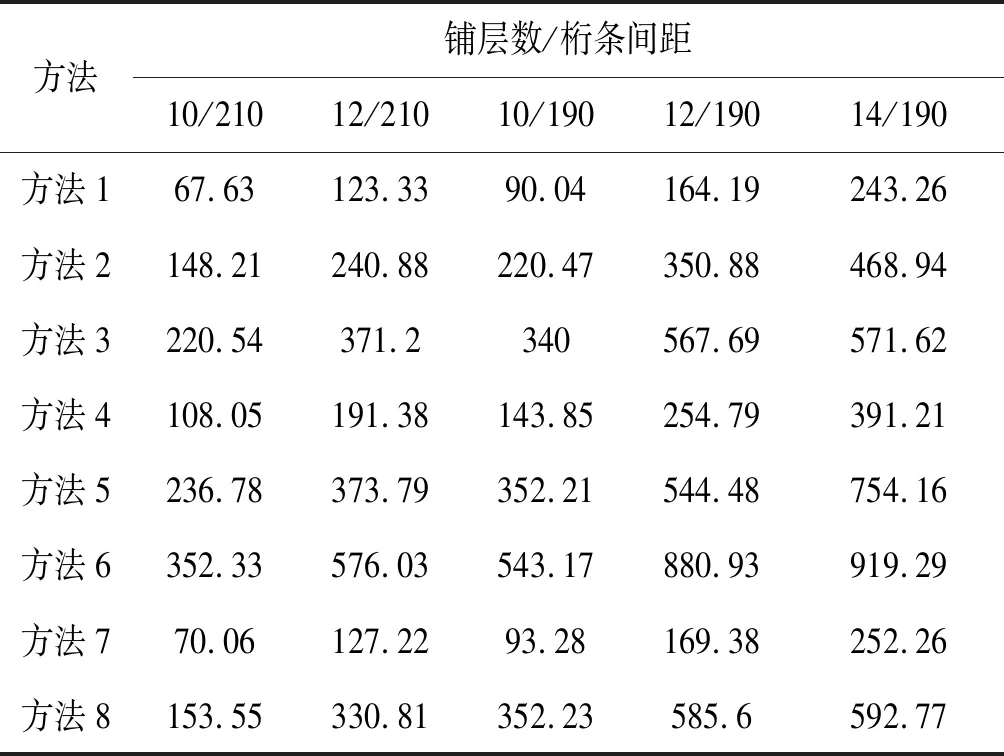
表7 工程理论方法计算屈曲线力 (单位:N·mm-1)

表8 试验值与工程理论计算值的误差

3 结论

从计算结果可知，复合材料帽型加筋壁板在轴压载荷作用下，局部蒙皮比加筋桁条屈曲载荷低，即局部蒙皮应先于长桁条发生屈曲，该计算结果与所有试验件轴向压缩屈曲试验相吻合。对于相同加筋桁条间距，蒙皮铺层越多，屈曲载荷越大；对于相同蒙皮铺层，筋间距越小，屈曲载荷越大。对于此文中的典型试验件及试验工况，用四边固支公式计算的屈曲载荷与试验值吻合最好，绝对误差值不大于10%。该试验件所用材料、铺层方式及铺层数、帽型加筋桁条、加筋桁条的间距在某大型飞机攻关研发方面作为典型使用，故四边固支公式计算的局部蒙皮初始屈曲具有参考借鉴意义。