基于NASTRAN的复合材料后梁稳定性优化设计与开口补强分析

张 讯 葛建彪 /

(上海飞机设计研究院，上海201210)

0 引言

飞机机翼、尾翼和机身上的薄壁加筋结构在承受压缩、剪切、扭转和弯曲等载荷作用时，最常见的失效模式为丧失稳定性，又称“失稳”或“屈曲”。为了保证结构的使用安全，需要进行稳定性研究，以控制结构的失效。机翼后梁是飞机上的主承力构件，其对强度设计要求严格，同时也是飞机机翼整体油箱的关键结构，其承受压缩、剪切、扭转和弯曲等载荷共同作用，受力复杂导致其易失稳破坏。为了保证结构的安全使用，在进行后梁结构设计时必须充分考虑其稳定性，对其结构稳定性进行优化设计[1]。复合材料相比于金属材料具有优良的力学性能，复合材料后梁已经作为一种先进的新材料结构，普遍应用于各种飞行器翼盒部件中。提高后梁结构在不同工况下的稳定性是工程设计的迫切需求。然而为了满足维修和安装的需求，在复合材料后梁结构上增开维修大开口后，对其结构稳定性又提出了更高的要求，因此必须在满足后梁静强度使用要求的基础上，对其结构稳定性进行优化设计[2-3]。为了满足后梁腹板的稳定性设计要求，本文运用理论计算手段和有限元软件MSC.Nastran在设计载荷工况下对后梁结构稳定性进行优化设计，以临界屈曲载荷不小于极限载荷为约束条件，对后梁结构立柱进行尺寸布局和截面尺寸的优化设计。首先对未开口后梁腹板进行了不同增强立柱数量下的腹板稳定性强度计算，然后根据计算结果对立柱数量和尺寸布局进行优化，再根据分析结果对开口的后梁腹板进行稳定性校核和“Z”形截面立柱尺寸进行优化，为后续复合材料后梁大开口补强设计提供技术支持。通过复合材料后梁稳定性优化设计解决了主承力结构的整体化设计、轻量化设计，其设计方法和设计理论均可以应用于其他主承力大开口结构设计。本文首先根据复合材料加筋壁板稳定性理论进行分析研究，其计算理论是在面内均匀分布载荷作用下，正交各向异性矩形平板的屈曲控制方程为[4-5]：

(1)

其中:Nx、Ny、Nxy为作用在壁板周边的单位长度上的载荷；w为屈曲时板的法向位移。

在对加筋壁板整体稳定性考核中，主要考察轴压(即Nx)对其稳定性的影响。具体模型如图1 所示。其中：L表示两肋间蒙皮长度；L′ 表示两桁条腹板中线距离；ts、tts、tds、tf分别表示蒙皮、上凸缘、下凸缘、腹板的厚度；wt和wd为上下凸缘的宽度；hf为腹板高度。两肋之间蒙皮可视为一加筋层压板，其欧拉屈曲载荷计算式为：

(2)

其中：Pe=cπ2EI/L2；λ为形状系数，桁条剖面为矩形时，λ可取1.2；c为加筋板的端部支持条件，不同的端部支持形式选取不同的值，本文加筋板可取1.0；G为桁条腹板的等效剪切模量；A为桁条中垂直腹板的剖面积；EI为加筋板剖面的弯曲刚度[6]。

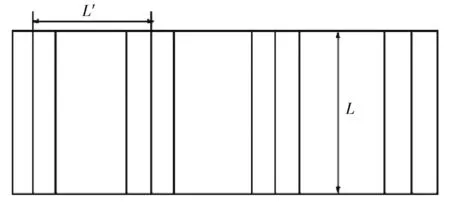
(a) 加筋壁板布局和尺寸

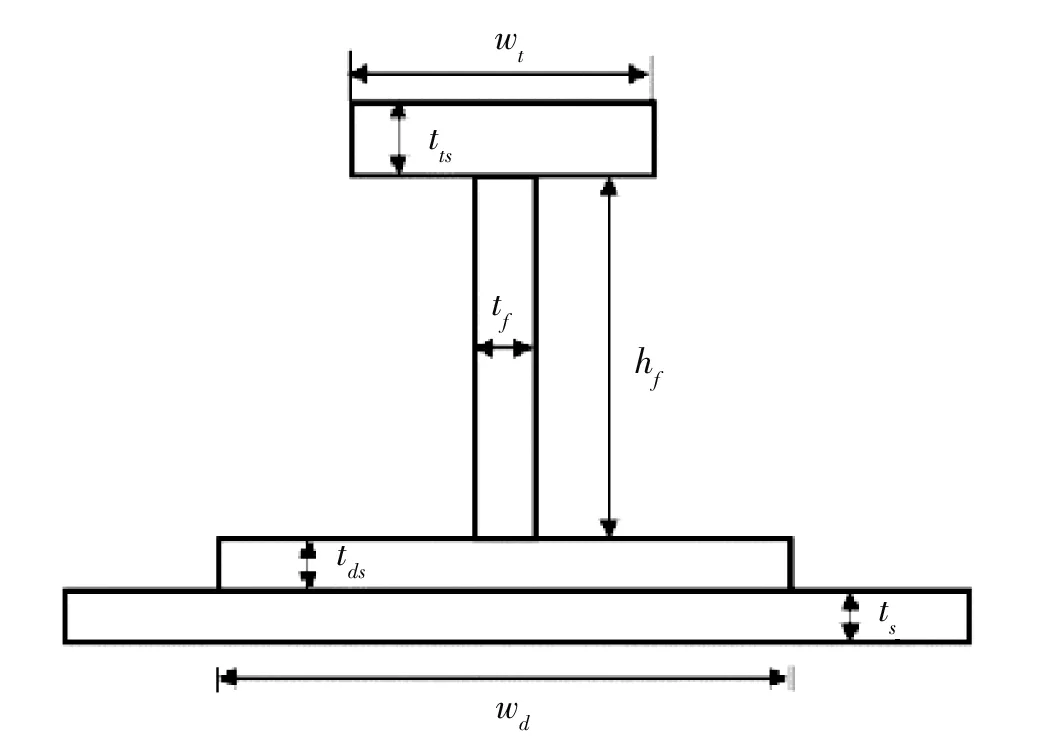
(b) 筋条详细几何尺寸图1 失稳分析理论模型

1 复合材料后梁结构设计

复合材料后梁是飞机机翼结构的关键结构，其承受飞机机翼的弯矩所引起的剪力和燃油压力载荷，其结构一般设计为组合梁式结构，由腹板和部分立柱组合而成，腹板主要承受由气密压力和机翼非对称载荷等引起的剪力和燃油压力载荷，立柱起到加强腹板强度和稳定性的功能。对于有大开口的复合材料后梁，立柱是防止后梁结构失稳的关键加强件，立柱数量和尺寸布局对后梁稳定性非常重要，需要在保证结构安全的设计原则下，优化其数量和位置、尺寸布局，为复合材料后梁大开口结构后续补强设计提供参数支持。

复合材料后梁的设计基本要求有：

1) 应变需求：应变水平在极限载荷下不得超过设计许用值。设计应有足够的厚度并用适当数量和尺寸的支柱加强，以提高腹板的屈曲应力；

2) 稳定性要求：飞机机翼结构常设计为具有储油功能的刚性油箱结构，其结构要求在极限载荷下不允许进入屈曲。

3)开口加强要求：后梁腹板上开口会造成腹板纤维切断，削弱结构强度。对于腹板上用于施工、检查等开口的位置，必须进行结构加强，以满足结构强度和稳定性要求[2]。

复合材料后梁腹板设计是后梁设计的主要结构部分，后梁腹板加强立柱可分为金属材料立柱和复合材料立柱，在综合考虑后梁试验安装及成本问题后，本文设计选用了金属材料立柱作为复合材料腹板的加强立柱，复合材料后梁首先设计了5个金属材料加强立柱进行布局。腹板材料为T700/BA9916单向带和ZMS2212织物，腹板铺层为[+/-/0/0/+/90/+/-/90/-/0/0/+/-/0]s，层数30，铝合金立柱的材料参数为：E=70Gpa，v=0.30。复合材料后梁结构初步设计如图2所示。

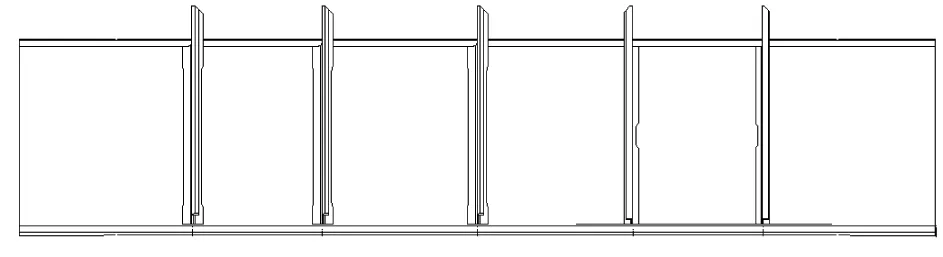
图2 复合材料后梁结构示意图

2 后梁结构优化设计和稳定性分析

2.1 复合材料后梁腹板立柱布局优化设计

为了设计复合材料后梁腹板的加强立柱数量和布局形式，本文采用理论公式和有限元仿真相结合的方法确定立柱的布局优化。假设所有立柱均满足稳定性支持刚度，可提供相对刚性的简支边界条件，然后计算两立柱中间腹板受四边简支约束条件下的最大临界剪切载荷，并与其实际受载情况进行比较，多次迭代后最终确定立柱布局[5-6]。

首先考虑常用的未开口复合材料后梁结构，再根据计算结果和开孔位置来调节后梁腹板立柱的布局，达到优化设计的目的。载荷工况的建立是优化分析的前提条件，根据复合材料后梁在飞机使用过程中承受的最大载荷来进行提取和模型建立，考虑后梁可能承受的最大弯矩和剪力，在设计分析过程中，可在极限载荷工况下对后梁结构稳定性进行分析和优化设计，计算分析的载荷工况如图3所示。

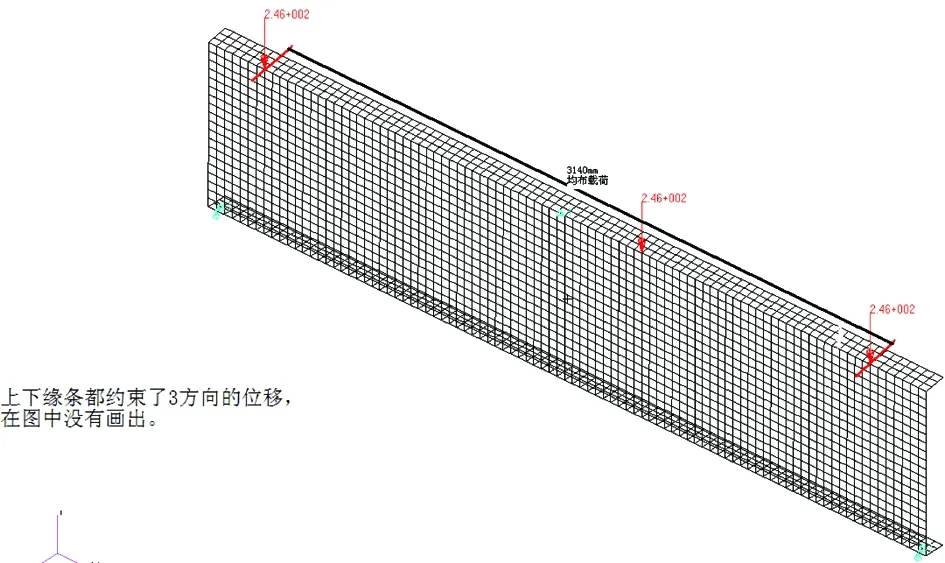
图3 后梁载荷力学模型

在立柱布局结构稳定性设计中，将立柱作为其所夹持的腹板部分的弹性支持，其支持刚度较简支边界更强。分析时，假定立柱为其所夹持的腹板部分的简支边界，分别采用理论计算和数值仿真在受剪载荷工况下对满足静强度要求的未开口后梁结构进行稳定性计算，从而完成对立柱布局的优化设计。为了简化分析模型，先用5个固定的加强立柱将腹板分为6个区域(其中两两对称)，尺寸如图4所示。采用理论求解和Nastran有限元软件相结合的分析方法，可以相互对应校核数据。

图4 5个固定立柱分区

1) 理论求解

复合材料后梁结构的失稳破坏主要发生在腹板上，在最不利载荷工况下，梁缘条承担绝大部分的弯矩，腹板发生剪切屈曲，按《复合材料结构设计手册》[2]正交各向异性矩形层压板的四边简支剪切屈曲载荷计算式如下[7-10]：

(3)

其中剪切屈曲系数Ks按无量纲参数α、β从《复合材料结构设计手册》中查取，四边简支板的剪切屈曲系数为C=0.132 44。根据腹板铺层顺序，抗弯刚度系数为D11=1 490 000 N·mm，D12=415 000 N·mm，D22=798 000 N·mm，D66=433 000 N·mm，腹板长a=3 700 mm，腹板高b=790 mm，α=0.85，β=0.25，取Ks=6，可求得此时腹板的失稳剪切荷载为Nxycr=88.5 N/mm。

2) 有限元仿真

后梁建模时对梁进行了有限元建模简化，其中，梁腹板简化为Quad4板单元，共14 742个单元，支柱简化为BAR梁单元，单根立柱有1 539个单元，五根共7 695个单元。腹板进行简支约束，上下缘条都约束三个位移方向，对其3 140 mm长范围内施加均匀分布剪切载荷246 N/mm。运用有限元软件Nastran对受剪载荷工况下后梁结构模型进行稳定性计算[11-13]，屈曲载荷系数为C=0.132 44，根据仿真计算结果，计算出该失稳载荷工况下腹板最大剪切载荷为：

与理论计算结果相比，屈曲时仿真计算所得最大剪切载荷减小了26%，这是由于在设计载荷工况下腹板虽然主要承受剪切载荷，但仍有相当大的弯曲载荷使得结构的屈曲承载能力降低。在该载荷工况下，腹板实际承受的最大剪切载荷为：

计算腹板屈曲时，最大失稳剪切载荷按1.5的安全系数选取，即屈曲系数达到1.5时，满足后梁腹板屈曲承载能力要求。因此，该后梁腹板的最大屈曲临界剪切载荷必须大于733.5 N/mm。

根据理论公式分别计算出5个加强立柱下的腹板6个区域的失稳剪切载荷分别为：179.3 N/mm、297.8 N/mm、216.5 N/mm、216.5 N/mm、297.8 N/mm、179.3 N/mm，此时结构的屈曲承载力为最小的179.3 N/mm。与设计计算的最大安全失稳剪切载荷733.5N/mm相比差距较大。5个固定加强立柱的后梁结构的屈曲承载能力不能满足要求。利用Nastran软件对该载荷工况下添加5个加强立柱的后梁结构模型进行稳定性计算，其中立柱位置先假定为简支边界条件，计算得到其屈曲载荷系数为C=0.419 48，屈曲模态如图5所示，屈曲模态为典型的剪切屈曲模态。

(a)一阶屈曲模态(1区屈曲)

(b) 二阶屈曲模态(1区屈曲)

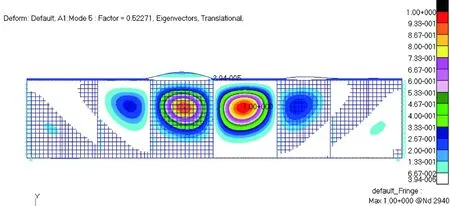
(c)五阶屈曲模态(3区屈曲)

(d)七阶屈曲模态(2区屈曲)图5 5个固定立柱简支边界后梁腹板屈曲模态

从有限元仿真中可以看出其第一阶屈曲模态也是发生在后梁端部区域，而被立柱隔开的各部分之间后续屈曲的先后顺序也与理论计算完全相同，可见数值分析与理论计算结果吻合较好。

根据仿真计算结果，计算出该失稳载荷工况下腹板最大剪切载荷为205.1 N/mm，与理论计算结果相比，屈曲时仿真计算所得最大剪切载荷增大了约10%，这是由于后梁腹板左右两端各有宽290 mm的部分复合材料铺层加厚了8层使得结构的屈曲承载能力提高。计算结果与后梁需承受的最大临界剪切屈曲载荷相比仍然很小，可见带5个固定立柱的后梁结构的屈曲承载能力不能满足要求，需进行进一步的立柱布局优化设计以提高结构的屈曲承载能力。将腹板加强立柱增加至11个，如图6所示。

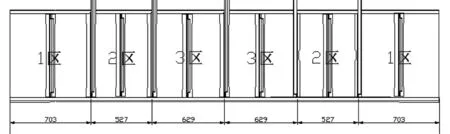
图6 11个固定立柱尺寸布置和分区

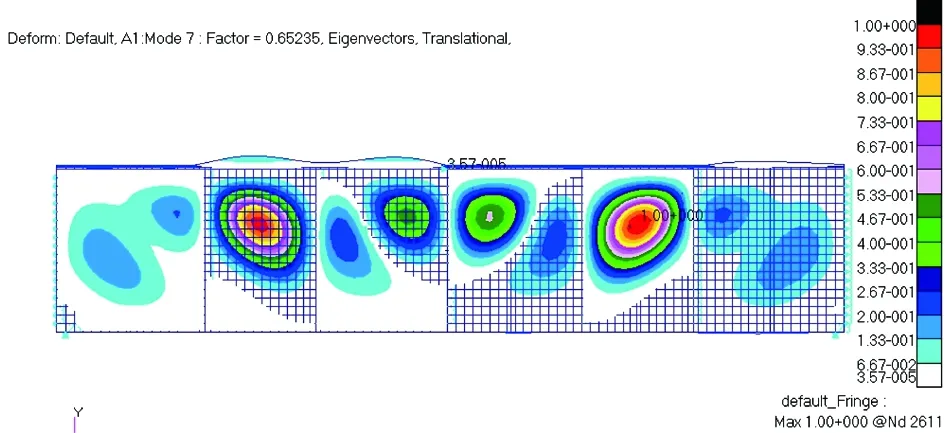
运用上述理论计算方法计算结果是1区先发生屈曲破坏，屈曲载荷系数为C=717.1/488.9≈1.467>1.319 8, 理论与仿真结果出现了偏差，这是因为随着载荷的增大，3区的弯曲应力绝对值渐渐增大，而1区的弯曲应力则小很多，实际存在的弯曲与剪切的耦合影响使得3区先发生屈曲破坏，如图7所示。

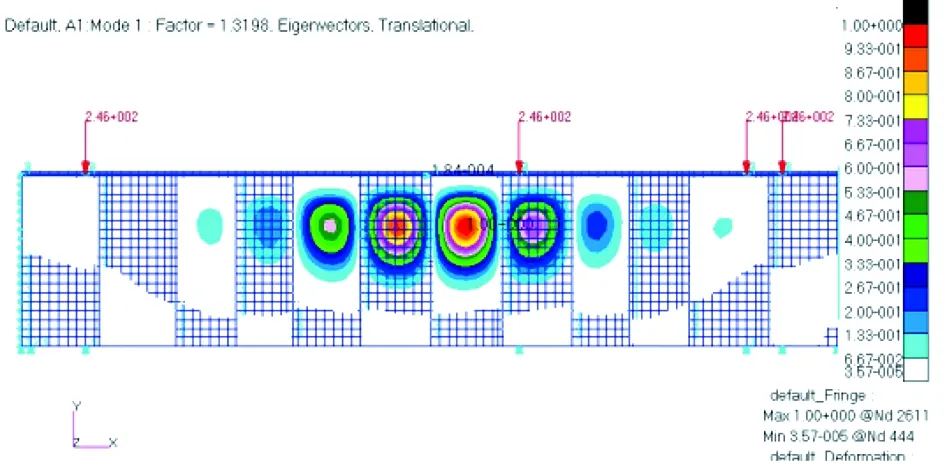
图7 带11个立柱后梁腹板屈曲模态

综合考虑理论计算结果和有限元计算结果，后梁结构的1区和3区的立柱布置均不能满足结构稳定性要求，需要再继续进行立柱优化布局设计。腹板增加15个加强立柱， 1区添加2个立柱三等分其间腹板、2区添加1个立柱两等分其间腹板、3区添加2个立柱三等分其间腹板，如图8所示。

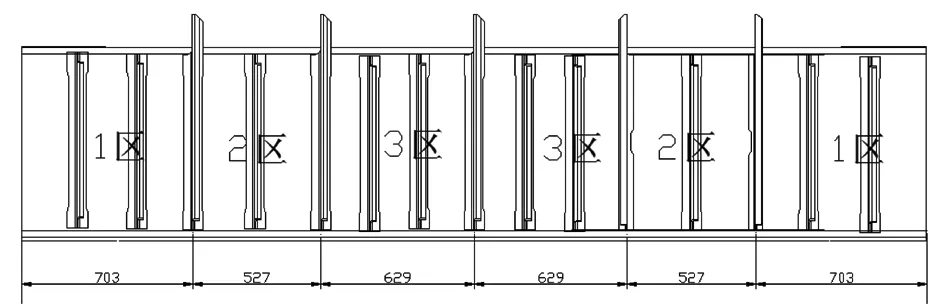
图8 15个立柱布置尺寸

15根立柱把腹板分割成16个求解区域，此次1区与3区求解宽度b减至b/3, 其他各参数基本不变，根据公式可知，理论屈曲承载力提高近9倍，满足后梁结构稳定性承载力要求。针对给定立柱布局进行稳定性计算，屈曲载荷系数为C=1.626 8，屈曲模态如图9所示，此时屈曲载荷系数大于设计目标值1.5，满足后梁结构稳定性承载力要求。

图9 带15个立柱后梁腹板屈曲模态

根据上述稳定性优化设计和分析，未开口复合材料后梁结构其立柱数量和布局设计按照稳定性要求完成设计。后续将对立柱的截面尺寸进行尺寸设计和分析。

2.2 复合材料后梁腹板立柱截面尺寸优化设计

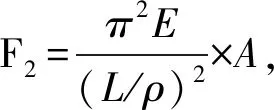
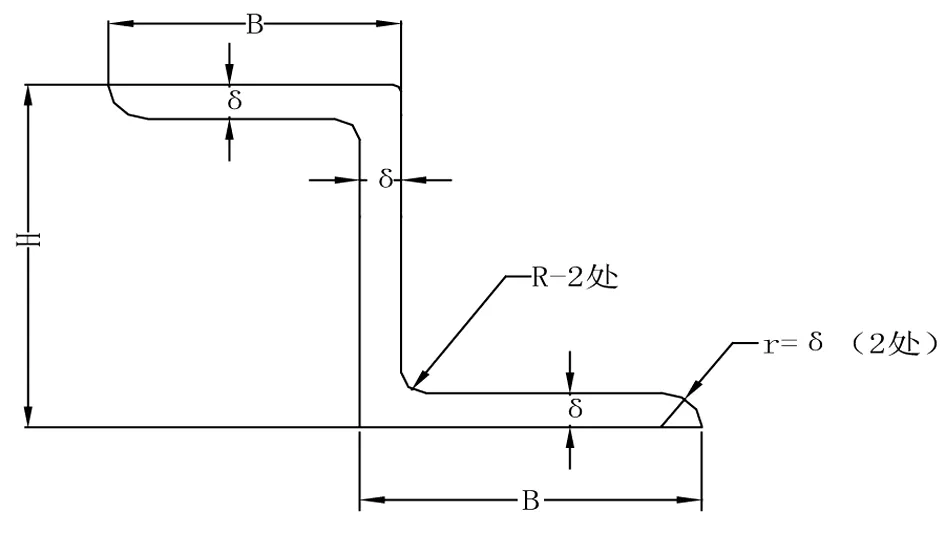
图10 后梁金属立柱“Z”形截面形式

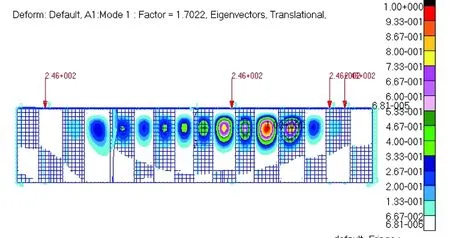
图11 带15个立柱后梁腹板屈曲模态

本文结合稳定性分析的有限元法, 以结构重量为目标函数, 将屈曲载荷作为约束函数，复合材料加筋立柱的高度H、厚度σ、宽度B等参数作为设计变量进行优化设计。根据前述腹板受剪失稳是按屈曲系数1.5 选取的，当立柱与腹板的屈曲载荷相差不大时会出现“等屈曲”现象，可能会降低加筋板的承载能力，因此为保证在腹板失稳定之前立柱不会失稳，取立柱屈曲系数为2进行有限元计算，即只允许腹板先于立柱发生屈曲。有限元计算时，将简支条件改回真实立柱约束条件，根据飞机型材图册中关于截面尺寸的规定进行立柱截面尺寸初选，然后反复迭代优化设计，在满足稳定性设计要求下其立柱截面尺寸最小，即重量最轻。最终优化确定的“Z”型立柱型号为(H=50.8 mm，B=31.75 mm，σ=2.4 mm)，截面面积为263.23 mm2。稳定性计算结果如图11 所示，其屈曲载荷系数为1.702 2，大于设计目标值1.5，满足设计要求。

3 开口后梁结构稳定性分析

开口将会对结构的承载能力造成很大的削弱，对满足静力要求的补强设计之前需要进一步进行屈曲承载验证，首先可根据未开口后梁结构设计的立柱布局进行开口补强后梁结构的有限元稳定性计算。

3.1 后梁大开口支柱补强稳定性计算

根据前文所得未开口后梁结构的立柱设计进行开口后梁结构有限元建模分析，图12所示为15根立柱按简支边界处理的后梁结构稳定性计算结果，与未开口计算结果相比，屈曲承载能力并无显著降低，且开口处未发生屈曲变形；图13为含有15根“Z”型立柱的后梁结构稳定性计算结果，建模过程中立柱与后梁腹板在螺栓点采用螺栓连接模拟，但忽略立柱与后梁腹板间的胶结处理以及接触问题，所得仿真结果偏小，但腹板的屈曲变形相差不大。

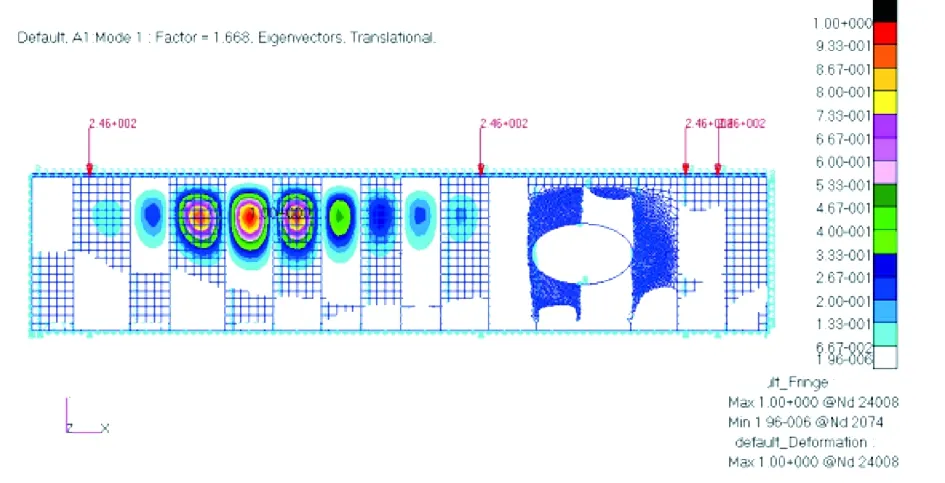
图12 带15个“Z”型立柱简支边界开口后梁结构腹板屈曲模态

图13 带15个“Z”型立柱开口后梁结构腹板屈曲模态

从以上两个计算结果可以看出，虽然采用不同的手段进行立柱建模分析，开口处均无屈曲变形。为避免开口处补强太多引起的质量浪费，减去开口正中间的被断开的立柱进行稳定性计算，采用简支边界和真实尺寸两种立柱建模方法的计算结果分别如图14所示，与以上两个计算结果相比，屈曲承载能力和屈曲模态都相差不大，因此此次立柱调整为14根是合理可行的。

图14 带14个“Z”型立柱开口后梁结构腹板屈曲模态

至此，对于”Z“型立柱补强后梁结构的立柱布局设计最终完成，具体布置尺寸如图15所示。

图15 “Z”型立柱位置布置图

4 结论

通过对复合材料后梁开口稳定性的分析和计算，得出以下结论：

1)提出了结构设计和稳定性分析的基本方法，为其他复合材料结构稳定性设计提供计算和分析方法；

2)随着屈曲承载能力的提高，弯矩对屈曲的影响越来越大，采用增加立柱的方法所得到的效果也越来越不明显，也增加了设计的复杂度，因此，如果要进一步提高屈曲承载能力，应该进一步增强支撑立柱截面面积和上下翼缘的尺寸，从而提高承载效率；

3)“Z”型立柱加强结构，对复合材料梁式结构稳定性加强作用明显。后续可通过更详细的优化设计方法来达到重量最优设计；

4)在给定的载荷工况条件下，利用理论计算与有限元仿真相结合的手段对后梁结构立柱进行布局了优化设计和截面尺寸设计，为复合材料后梁详细设计提供了参数支持。