多层土地基扩底抗拔桩离散元颗粒流研究

李飞，杨俊杰，宋琦，孙涛

(1.中国海洋大学海洋环境与生态教育部重点实验室，山东青岛，266100；2.中国海洋大学环境科学与工程学院，山东青岛，266100；3.昌大建筑科技有限公司，山东潍坊，261000；4.山东科技大学地球科学与工程学院，山东青岛，266590)

离散元方法适用于诸如散体材料的破坏准则、非饱和状态下的材料抗剪强度等问题[1]。NARDIN等[2]根据定义的离散元颗粒流接触模型建立了细观参数与宏观力学特性的定性关系。砂土是一种散粒体介质，在结构体荷载作用下的本构关系非常复杂，而颗粒流作为一种基于离散单元而开发的数值模拟方法[3]，可以很好地模拟近似圆形颗粒介质法向、切向和滑移作用关系的运动。刘文白等[4−5]运用现场试验及颗粒流理论，研究了黄土中扩底桩承受上拔荷载的宏观及其细观力学结构性能；柴浩等[6−7]结合颗粒流理论，研究了黏土地基中挤扩支盘桩受上拔荷载时，荷载−位移关系、土体变形破坏及地基位移场分布；周健等[8−9]通过颗粒流模拟研究了等截面桩桩端和桩周土体的孔隙率变化规律；王浩等[10]从桩端周围土体位移场、应力场和孔隙率变化等角度，研究了砂土中桩端阻力随位移发挥的内在机理；陈亚东等[11−13]从单桩的宏观和细观工作性质进行了研究；李阳等[14−16]从细观角度研究了分层土中桩土相互作用和桩基受力特性。目前，针对扩底桩的颗粒流细观分析还不够深入和完善，现有颗粒流数值模拟多偏重于单层土中压入桩或等截面桩的研究。基于此，本文以室内模型试验为研究基础，通过建立与扩底桩承载特性、地基变形特征及对破坏模式产生影响的宏观和细观参数之间的内在联系，从细观角度分析扩底抗拔桩桩周土颗粒的位移、应力分布及破裂面的形成规律。

1 模型试验简述

1.1 试验概况

本文依托的模型试验共2组13个。第Ⅰ组有8个试验，研究持力层厚度对扩底桩单桩抗拔承载特性的影响；第Ⅱ组有5个试验，研究持力层密度对扩底桩单桩抗拔承载特性的影响。

模型箱由1个铁质半圆筒与钢化玻璃隔板拼接而成，半圆筒内径为800 mm，高为1200 mm，壁厚为10 mm，钢化玻璃厚为12 mm[17]。使用KYOWA EDX-10A 型采集仪对荷载、位移以及桩身应变实施同步采集，采集频率设为1 Hz，加载方式为应变控制式，加载速率为1 mm/min。

图1所示为模型桩尺寸示意图，由图1 可见：1 号和2 号扩底桩长分别为730 mm和790 mm，埋置在土中的长度分别为710 mm和770 mm，模型桩主桩桩径为20 mm，扩大头直径D为40 mm，高度为20 mm。因此，模型桩入土长度与扩大头直径之比约为17.8。试验用模型桩的抗拔弹性模量为67.63 GPa，抗拔刚度为2 947.99 kN。

模型箱内径与扩大头直径之比为20，可以忽略模型箱的边界效应[18−19]，试验用土石英砂，分别使用0.1 mm 与1.0 mm 标准筛筛分，取粒径为0.1～1.0 mm的砂作为试验用砂，并在扩大头附近铺设染色砂作为标志层。试验用土的基本物理性质如表1所示。砂土不均匀系数为2.38，曲率系数为1.29，均匀性良好。模型地基相对密度分别为0.55±0.05(中密)和0.94±0.05(密实)。

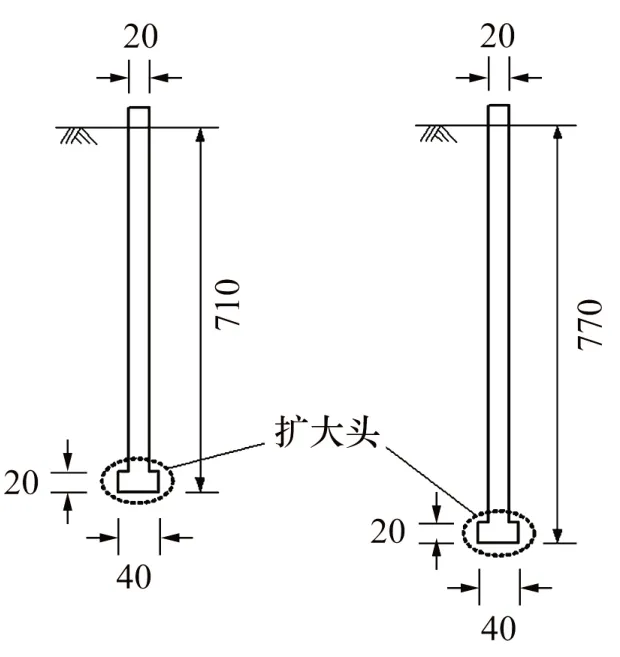
图1 模型桩尺寸示意图Fig.1 Schematic diagram of model pile size

表1 试验用土的基本物理性质Table 1 Basic physical properties of soil for testing

1.2 试验结果

1.2.1 抗拔承载力（第I组试验）

图2所示为基于持力层厚度变化的单桩荷载-位移(Q-s)曲线。由图2 可知：荷载随桩顶位移逐渐增加，随着位移增大，荷载增加速率逐渐变小。当H/D超过2.5 时，极限承载力不再增加，此时，极限承载力稳定在187.82～194.55 N，是H/D=0.5时极限承载力(50.92 N)的3.7～3.8 倍。因此，为充分发挥扩大头作用，可以把H/D=2.5作为扩底抗拔单桩持力层厚度的临界值。采用双曲线拟合方法[17−20]确定极限承载力，结果如表2所示。

表2 单桩抗拔极限承载力Qu(持力层厚度不同)Table 2 Ultimate bearing capacity of single pile Qu(different bearing layer thicknesses)

1.2.2 抗拔承载力（第Ⅱ组试验）

图3所示为持力层密度发生变化时的单桩抗拔Q-s曲线。由图3 可知：桩顶位移在0～3 mm 时荷载增加速率较快，随着位移增大，荷载增加速率逐渐变小后趋于平稳。采用双曲线拟合方法确定极限承载力，结果如表3所示。

图3 不同持力层密度下的单桩抗拔Q-s曲线Fig.3 Pull-up Q-s curve of single pile with different bearing layer density

表3 单桩抗拔极限承载力Qu(持力层密度不同)Table 3 Single pile uplift ultimate bearing capacity Qu(different bearing layer density)

2 颗粒流模型的建立

目前普遍采用的宏观有限元分析方法可以获得桩的承载力和变形特性。但随着桩体上拔量的增加，桩底环境变得复杂，扩大头周围土体位移出现非常规变化，从宏观角度进行的模拟无法更真实地体现土颗粒的细观运动规律。而离散元以土颗粒为单元，可以合理地描述桩土的位移及变形规律，且单元数目可以按照模型几何尺寸有针对性地设定，以满足对桩承载力及砂土变形的分析要求。

2.1 建立模型

运用PFC软件[1]，编写颗粒流代码，通过试算后选择相匹配的颗粒及墙体参数，构成符合数值模拟的计算模型，接触模型采用线性接触。

颗粒数量直接影响数值模拟的计算速度与精度，因此，在进行颗粒流模拟之前，需要选取最合适的颗粒数量。图4所示为颗粒数量与轴向峰值应力的关系。由图4可见：随模型体颗粒组成数量的变化，模型轴向峰值应力在初始阶段呈现波动特征，当颗粒数超过2.0×104个后，纵轴基本维持稳定，因此，本文模型中共生成2.0×104个砂土颗粒。

图4 颗粒数量与轴向峰值应力的关系[1]Fig.4 Relationship between particle number and axial peak stress[1]

考虑到与模型试验相匹配，采用的模型箱高为1 100 mm，宽为800 mm，1 号桩和2 号桩几何形状与模型试验的一致，如图5所示。

2.2 确定模型参数

图5 扩底单桩颗粒流模型Fig.5 Expanded single pile particle flow model

通过匹配计算或数值仿真试验等方法建立颗粒流细观力学参数与土体宏观力学参数之间的联系[21]，并通过参数试算和分析[22−23]得到土层颗粒的法向刚度和剪切刚度，桩和模型箱墙体的法向刚度和剪切刚度，颗粒及墙体的摩擦因数。砂土由颗粒形成，模型箱、模型桩由墙体形成。颗粒流模型基本参数如表4所示。

2.3 确定加载方式

对构成桩的墙体施加速度，完成加载。这一过程等同于模型试验中控制位移的加载方式。在程序中，采用匀速加载，加载速度控制为4×10−5m/时步。控制总上拔量为10 mm。在加载过程中，监测桩的荷载−位移变化情况，研究桩周土体位移、力链的发展规律。

3 持力层厚度对抗拔承载特性的影响

3.1 抗拔承载力的颗粒表现

图6所示为不同持力层厚度Q-s曲线(数值模拟)，模型试验和颗粒流模拟方法得到的H=0.5D，H=2.5D扩底桩单桩抗拔(Q-s)对比分析曲线。由于接触的归属问题和扩大头附近颗粒接触数量的变动，使曲线发生了一定波动，但数值模拟得出的结果与模型试验结果基本一致，证明了颗粒流理论在参数选择上的合理性。

表4 颗粒流模型基本参数Table 4 Basic parameters of particle flow model

由图6(c)可见：静止状态下的砂土颗粒在重力作用下处于相对均匀分布状态，施加荷载后，0～2 mm位移区间荷载增加速率较快。随着桩顶上拔位移增大，颗粒趋于密实，土颗粒间的作用应力加强，荷载增加速率逐渐变小而后趋于平缓；当H/D超过2.5 时，极限承载力得以充分发挥。土体表现出来的承载特性是其系统内部各种要素共同作用的结果，与土的细观结构存在一定联系。

3.2 荷载分担规律颗粒位移表现

3.2.1 荷载分担比

通过颗粒流数值模拟分析发现，扩大头阻力和桩侧摩阻力均随桩顶位移逐渐增加，开始快速增加，但随着位移增大，荷载增加速率逐渐变小。图7所示为扩底桩荷载与桩顶位移的关系。由图7可见：稳定后的扩大头阻力从20.77 N 增加至106.13 N，2.5D时扩大头分担的荷载是0.5D荷载的5.1 倍；当H/D超过2.5 时，扩大头阻力不再增加，桩顶荷载分担比始终大于扩大头荷载分担比。

3.2.2 接触力分布

图8所示为持力层厚度为2.5D的扩底桩桩周土体随桩位移发生变化的力链图。力链短线的方向代表力的传递方向，粗细代表接触力。接触力主要分布在桩体的中下部。扩大头附近区域砂土承受颗粒间的接触力较大，随着上拔位移的增加，接触力逐渐向土体外围发展；当s=1.5 mm 时，扩大头开始发挥作用，上端土体被挤密；当s=4.0 mm时，随着上拔荷载增加，桩侧及桩端阻力同比例增加，力链发展区域扩大；当s=7.5 mm 时，接触力向斜上方均匀延展；当s=10.0 mm 时停止加载，荷载分担比保持平衡。

图9所示为极限荷载作用下H=2.5D模型试验地基变形过程，图9中将桩土相对位移划分为4个区域。从图9可见：桩顶抗拔荷载作用下，区域A土体首先发挥作用，但该区域的侧摩阻力影响范围不大，区域A′力链较少，说明扩底桩中上部桩侧摩阻力对桩承载力的贡献率偏低；在工作荷载条件下，扩大头开始发挥作用，扩大头上部土体受到挤压，区域B是扩底抗拔桩的主受力区，对应区域B′。由于扩大头的存在，砂土沿着扩大头的边缘向斜上方发展并在达到区域B的最远端受力区后向桩内侧区域A收拢，区域C反映了扩大头桩侧土体颗粒位移变化情况，区域C′的力链分布也较小，对抗拔承载力的贡献率不高；力链图中的力链从区域B′向斜上方延伸，从传递方向可以清晰地判断竖向荷载作用下扩大头两侧一定范围土层中土颗粒的应力发散方向，应力产生差异的地方即为桩土破裂面形成的地方；区域D 是抗拔桩的桩底悬空区，桩上拔过程中，扩大头底部的吸附力使少部分砂土回流，随着荷载增加，吸附力逐渐消失，区域D′仅存在很少的力链，证明了试验模拟的合理性，也进一步通过细观角度验证了在宏观理论及试验研究中[25−26]桩底存在吸附力。

图6 不同持力层厚度下Q-s曲线(数值模拟)Fig.6 Q-s curve with different bearing layer thicknesses(numerical simulation)

图7 扩底桩荷载与桩顶位移的关系Fig.7 Relationship between excavation pile loading and pile top displacement

图8 不同桩顶位移下接触力分布图(H=2.5D)Fig.8 Contact force distribution diagram under different pile top displacement(H=2.5D)

3.2.3 持力层厚度不变荷载分担比颗粒表现

图10所示为不同位移条件下扩大头阻力占桩顶荷载比例与H/D的关系。由图10 可见：当H/D一定时，扩大头阻力占桩顶荷载的比例随桩顶位移逐渐增加，接触力向斜上方延展；当桩顶位移超过4 mm时，扩大头阻力占桩顶荷载的比例不再增加；当H/D超过2.5时，扩大头阻力占桩顶荷载的比例为36.42%～40.18%，是H/D=0.5 时扩大头阻力占桩顶荷载平均比例(20.50%)的1.78～1.96倍。

3.3 地基变形规律的对比

图9 极限荷载作用下模型试验地基变形与颗粒流力链对比Fig.9 Foundation deformation and particle flow force chains comparison of single pile uplift model test under ultimate load

图10 扩大头阻力占桩顶荷载的比例与H/D关系Fig.10 Relationship between ratio of the head resistance to the top load and the H/D

为进一步分析土颗粒的移动规律，研究H=2.5D在1/2极限荷载(97.28 N)和极限荷载(194.55 N)作用下扩大头周围砂土颗粒的位移场，如图11所示。由图11(a)可见：在1/2极限荷载作用下，桩侧0.5D范围内土体受到桩的扰动，土颗粒主要沿着桩侧竖向移动，与桩产生相对位移，在桩体的中上方形成沿桩体竖直方向的破裂面；扩大头上部土体发生挤压的效果比较明显，破裂面在此处向斜上方延伸，达到远端后内收，与桩中上部形成的破裂面汇合。扩大头顶部土体的相对位移虽有变化，但差别并不大，土体处于弹性状态，扩大头周边仅顶部一定范围内的土体受到挤压，土应力向四周发散的范围有限，扩展角为25°左右，如图11(b)所示。

由图11(c)可见：在极限荷载作用下，扩大头承担40.18%的抗拔荷载，桩侧1.0D范围内的桩侧土体受到扰动，桩侧土体先于扩大头部位受力，在扩大头顶面出现与1/2极限荷载作用相同的土颗粒先外延然后内缩的现象，但应力发展区域的角度大于1/2极限作用下的应力。由图11(d)可见：处于扩大头顶部及桩周交界范围内土压力变化更为复杂，土压力剧烈变化的范围也越来越大，桩端顶面土压力逐渐增大；破裂面角度逐渐增大，扩大头远端土体受干扰程度较小，土颗粒的相对移动在此处停止；土压力发生变化的部位同时反映荷载传递过程中桩底土逐渐屈服的过程，破裂面扩展角度保持在32°左右。

图12所示为不同持力层厚度地基变形特征(模型试验)，图13所示为不同持力层厚度地基变形特征(数值模拟)。从工作荷载加载至极限荷载，扩大头上部土体发生局部压缩−剪切破坏，破坏面从扩大头顶面边缘沿倾斜直线向上扩展，在水平方向影响范围达到最大后向桩侧收缩，与桩体上部沿桩体形成的破裂面连接。将试验图像右侧进行处理，可以发现持力层厚度从0.5D增大至2.5D，破坏面的起始扩展角度从25°增大至32°，剖面上形成椭圆形破坏面，水平方向破坏范围为2.3D～3.3D，竖直方向破坏范围为2.0D～3.5D。当持力层厚度超过2.5D时，扩大头影响范围不再增加。持力层越厚，地基破坏区域越大，极限抗拔承载力也越大。

图11 H=2.5D时颗粒位移场Fig.11 Particle displacement field when H=2.5D

图12 不同持力层厚度地基变形特征(模型试验)Fig.12 Deformation characteristics of different bearing layer thickness foundations(model test)

图13 不同持力层厚度地基变形特征(数值模拟)Fig.13 Deformation characteristics of different bearing layer thickness foundations(numerical test)

根据离散单元体的基本假设，在单个时间步长期间，颗粒运动的速度保持恒定，作用在任意断面上的颗粒始终由与其接触的桩附近砂土颗粒的相互作用唯一确定。数值模拟得出的砂土破裂面形态及扩展角度与模型试验结果基本一致，证明通过动态变形全过程研究承载特性的模型试验可以很好地表征扩底桩在多层土地基中砂土颗粒的位移及破裂面形态。

4 持力层密度对抗拔承载特性的影响

4.1 抗拔承载力的颗粒表现

持力层厚度超过2.5D，抗拔承载力不再增加，因此将持力层厚度设置为3.0D，研究持力层密度对单桩抗拔承载特性的影响。图14所示为通过颗粒流模拟分析得到的不同密度持力层Q-s曲线。

图14 不同密度持力层Q-s曲线Fig.14 Q-s curves of different density bearing layers

对比试验3和试验5发现：扩大头置于密实的持力层中，即使桩长相对较短，其极限承载力仍要比扩大头置于较松软的持力层大。对比试验2和试验5发现：当桩长相同时，密实持力层极限承载力远比较松软持力层的大；试验4极限承载力是试验1的4.9 倍，说明将扩大头置于密实土层中可以有效提高桩的极限承载力；试验4和试验5的极限承载力基本相同，进一步说明持力层达到临界值后，继续增加持力层的厚度不会显著提高扩底抗拔桩的极限承载力；持力层为密实砂(相对密度为0.94)时的极限抗拔承载力是中密砂(相对密度为0.55)3种试验情况下的1.3～5.1倍。

4.2 不同密度土层桩土接触力分布特征

图15所示为扩大头阻力占桩顶荷载的比例与桩顶位移的关系。从图15 可见：在加载初期，桩顶位移较小，扩大头分担的荷载比例随着桩顶位移增加较快；达到极限荷载时，扩大头分担的荷载比例趋于稳定。试验5和试验4扩大头分担的荷载比例峰值稳定时为35%～40%，对应的桩顶位移约为4 mm；试验3的荷载比例峰值稳定时为30%左右，对应的桩顶位移约为3 mm，曲线波动趋于平稳；试验1和试验2稳定时为20%左右，对应的桩顶位移为1.0～1.5 mm。试验4和5的扩大头荷载分担比是试验1，2和3的1.5倍左右。持力层密度越大，扩大头分担的荷载比例越大，扩大头分担的荷载达到稳定需要的桩顶上拔位移也越大。

图15 扩大头阻力占桩顶荷载的比例与桩顶位移的关系Fig.15 The relationship between the ratio of pile tip resistance to load on pile top and pile top displacement

4.3 地基变形规律

图16 不同密度持力层地基变形特征(模型试验)Fig.16 Deformation characteristics of foundations with different bearing layer densities(model test)

图17 不同密度持力层抗拔单桩桩周土体位移图(数值模拟)Fig.17 Displacement diagram of soil around the pile with different densities of bearing layer(numerical test)

图16所示为不同密度持力层地基变形特征(模型试验)，图17所示为不同密度持力层抗拔单桩桩周土体位移图(数值模拟)。在相同桩顶荷载作用下，5种不同密度土层的桩土接触力表现出不同破裂面形态，可以发现如下规律：1)试验1与试验4靠近桩的砂体移动方向基本一致，沿扩大头向上移动，但由于试验4中砂的密度比试验1的大，使得试验4的砂土位移的扩展角及扩展面积比试验1的大；2)试验2的扩大头置于中密砂土中，砂土位移竖直向上发展，试验5的扩大头密实砂持力层中，砂土位移成椭圆形向斜上方发展，极限承载力远高于前者；3)试验4 与试验5的砂土位移相似，承载力基本相同，说明当满足一定厚度持力层(2.5D以上)时，即可达到等密度单层土同样的桩体承载力，试验5的方案更合理并具有实用价值。

5 结论

1)当持力层厚度超过2.5D时，接触力及砂土颗粒形成的破裂面角度趋于稳定，极限承载力、扩大头分担的荷载及地基破坏区域均不再明显增加。极限承载力、扩大头分担的荷载及地基破坏面水平方向与竖直方向的影响范围分别是持力层厚度为0.5D时的3.7～3.8 倍、5.1 倍及1.4 倍和1.7倍；扩大头阻力占桩顶荷载的比例稳定在36.42%～40.18%，是H/D=0.5时扩大头阻力占桩顶荷载平均比例(20.50%)的1.78～1.96倍。

2)扩大头上方的土体发生压缩变形，扩大头顶部边缘的土体发生局部剪切变形。随着荷载继续增加，土体发生剪切和压缩的范围逐渐向上扩展，沿扩大头顶面边缘向上发展出近似椭圆形的破坏面。持力层是密实砂(相对密度为0.94)时的极限抗拔承载力和扩大头分担的荷载分别为中密砂(相对密度为0.55)的1.3～5.1倍和1.5倍。

3)不同密度土层在相同抗拔荷载作用下，扩大头周围桩土破坏面的影响范围不同，这也是在相同抗拔荷载作用下，扩大头周围破裂面形态在土层密度不同条件下存在差异的主要原因，数值模拟分析结果与模型试验分析结果一致。

4)颗粒流理论从细观角度模拟扩底单桩的竖向承载特性，可与室内模型试验共同揭示砂土在受竖向荷载作用下的内部变形及接触力变化等方面的特征。