基于球面对称设计的离散元细观参数定量确定方法

2019-04-17彭霞饶秋华李卓张杰

中南大学学报（自然科学版） 2019年11期

彭霞，饶秋华，李卓，张杰

(中南大学土木工程学院，湖南长沙，410075)

在深部采矿、地热开采、隧道开挖等岩体工程中，岩体内部含有的多种缺陷(如孔隙、裂纹、节理等)在长期荷载作用下会发生损伤演变，造成工程安全隐患，因此，研究岩石破坏的宏−细观机理对岩体工程的安全评定、防灾减灾等具有重大的理论指导意义。连续介质力学难以解决多裂纹扩展问题，且实验研究存在一定的局限性。目前，数值方法已成为研究岩石细观破坏机理的有效方法，其中，基于非连续性介质理论的颗粒流软件PFC(particle flow code)[1]已广泛应用于岩土工程领域。颗粒流软件(PFC)是将材料离散成刚性颗粒后，通过模拟颗粒间的相互运动及其作用来研究真实材料的力学特性，其前提条件是选取合适的细观参数。孟京京等[2−3]采用“试错法”标定PFC细观参数，但由于细观参数因素多且标定具有一定的盲目性与不确定性，导致标定周期长，模拟试验次数多。YOON等[4]采用PB(Plackett-Burman)设计法测试细观参数对宏观参数(如单轴抗压强度、弹性模量、泊松比等)的敏感性，选取影响最大的2个细观参数，再通过CCD(central composite design)设计法建立宏−细观参数之间的非线性关系，可以求得细观参数，但每个宏观参数仅由较少的细观参数确定，没有考虑其他细观参数对宏观参数的影响。周喻等[5]采用BP(back propagation)神经网络法方法，建立了宏−细观参数的非线性模型，输入宏观力学参数，即可得到岩土体细观力学参数，但BP神经网络模型的创建、学习、训练需要大量的随机组合样本。陈鹏宇等[6]对细观参数进行正交设计，以多因素分析、量纲分析研究宏−细观参数之间的关系，确定的函数关系式只考虑单个细观参数的影响，提出了试错法标定细观参数的具体流程。目前，对于PFC 细观参数的定量确定方法仍较少。为降低模拟试验次数且提高精度，需引入一种新方法来定量建立PFC宏−细观参数关系式。盛海林等[7]提出了球面对称设计法，在球面上均匀、对称地选取试验点，通过试验建立了自变量与因变量之间的关系，该方法具有试验次数较少、精度较高等优点，更适用于多因素、多水平试验。本文采用球面对称设计法，建立PFC2D宏−细观参数定量关系式。依据材料宏观力学参数定量确定其细观参数，模拟计算单轴压缩下完整岩石试件的应力−应变曲线和宏观力学参数、含多裂纹岩石试件的断裂轨迹，并与试验结果进行对比验证，以便为PFC 细观参数的定量分析提供一种有效方法。

1 球面对称设计法

在球面对称设计方法中，设因素个数为n，则球的半径r为n的平方根，球的空间维数等于n，在该球面上均匀、对称地选取试验点。考虑到任意因素对各因变量的影响均有一定范围，将这些范围以一定的代码予以统一，规定每个因素有5个水平，分别用−r，−1，0，+1和+r共5个代码表示，其中，各因素水平代码−r，0和+r对应的值分别为该因素范围的最小值、平均值、最大值；根据任意2个水平代码差的比值与该水平代码对应值差的比值相等的原则，可得到各因素水平代码−1和+1 对应的值。试验次数包含3 部分：所有因素的水平代码仅为−1或+1的试验次数(2n次)；1个因素水平代码为−r或+r、其余因素水平代码为0的试验次数(2n次)；各因素水平代码为0的试验次数(1次)。总试验次数为2n+2n+1次。

以5因素为例建立球面对称设计表。设5个因素为X1，X2，X3，X4和X5，即n=5，球半径r=5，则各因素的5个水平代码为-5，−1，0，+1和+5。在设计表中，总列数为6(第1列为试验次数号)，其余每一列元素为某一因素在每次试验中的水平代码；总行数与试验总次数43(25+2×5+1)相同，每行元素为5个因素的某个水平代码(5个水平代码之一)。其中，第1～32行(2n次试验)中的每一行是各因素的水平代码−1 或+1的任意组合，且各行不重复；第33～42 行(2n次试验)中的每一行是某一因素水平代码为-5 或+5、其余因素水平代码为0的任意组合，且各行不重复；第43 行为各因素水平代码为0的组合。由此可得5因素球面对称设计表，见表1。

2 细观参数计算公式

2.1 PFC2D建模

在PFC2D 中，颗粒之间通过黏结产生相互作用，黏结模型包含接触黏结模型、平行黏结模型、平直节理接触模型3种[8−9]。接触黏结模型中的圆形颗粒与颗粒之间为点接触，因此，不能传递力矩，当法向或切向力超过对应的黏结强度时，黏结破坏。平行黏结模型中两圆形颗粒间由平行键黏结，可以传递颗粒之间的力与力矩，该模型比接触黏结模型更接近于岩石材料真实受力情况，应用更广。平直节理接触模型是将多边形颗粒代替圆形颗粒，能够传递力与力矩，同时能抑制颗粒黏结破坏后的旋转，但需要确定更多的细观参数。

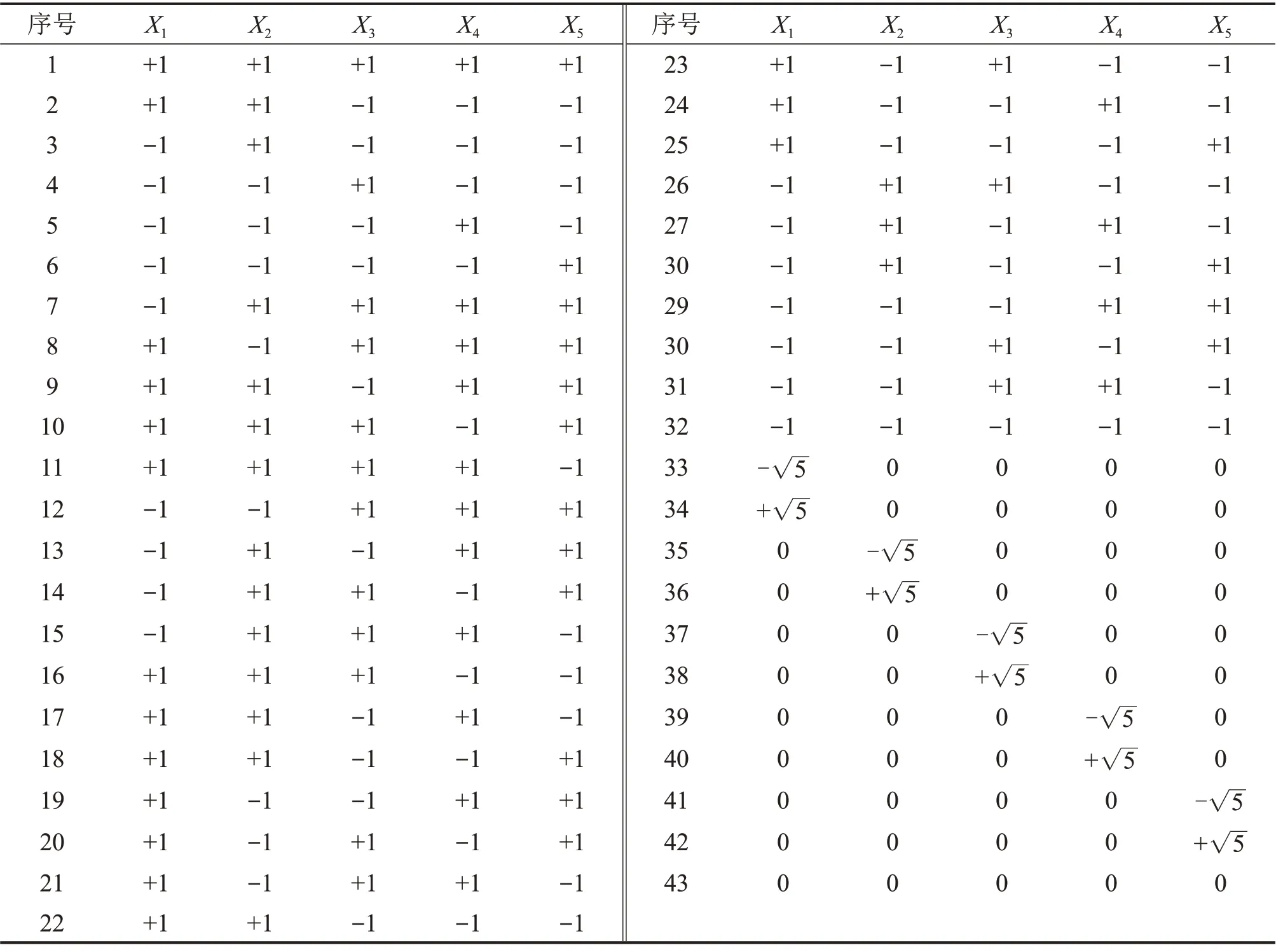
表1 5因素球面对称设计表Table 1 Spherical symmetric design table of five factors

本文选取平行黏结模型，其细观参数如表2所示。为简化计算，进行以下假设[9−11]：；。设平行黏结法向应力强度与法向应力强度之比σn/σs=m(m为比例系数)，本文取m=1[12−13]，故待定的独立细观参数为6个，即Rmin，Ec，kn/ks，σn，μ和Rσ。

在PCF2D 建模中，先确定模型的最小颗粒半径Rmin。研究结果表明[14−15]，当Rmin小到一定程度时，宏观力学参数计算结果变化不大，但Rmin过小会降低数值模拟计算效率。为得到合适的Rmin，以岩石单轴压缩试验为例说明。采用长为100 mm、宽为50 mm的长方形标准试样，选取4 种不同的Rmin(0.1，0.2，0.3和0.4 mm)进行建模，如图1所示。设其他细观参数为：，模拟计算不同Rmin下的岩石宏观力学参数。由表3 可见计算得到的弹性模量E、泊松比v、单轴抗压强度σc均在岩石的宏观力学参数范围内[16]，E=10～70 GPa，v=0.15～0.30，σc=50～200 MPa，表明所选取的细观参数是合理可行的；当Rmin减少至0.1 mm时，E，v和σc的计算结果与Rmin=0.2时所得结果变化不大，但当Rmin=0.2 mm 时，所需生成的颗粒数目比Rmin=0.1 mm 时大大减少，因而，选定Rmin=0.2 mm。待定的独立细观参数只有5个：Ec，kn/ks，σn，μ和Rσ。

表2 PFC2D平行黏结模型中的细观参数Table 2 Microscopic parameters of PFC2D parallel bonded model

图1 单轴压缩下岩石试件PFC2D模型(Rmin=0.2 mm)Fig.1 PFC2D model of rock specimen under uniaxial compression(Rmin=0.2 mm)

表3 不同Rmin下岩石宏观力学参数的模拟结果Table 3 Simulation results of macroscopic mechanical parameters of rock with different Rmin

2.2 细观参数范围确定

利用球面对称设计法确定PFC2D细观参数时，首先需根据宏观参数的范围确定细观参数的取值范围。对于岩石材料，其宏观力学参数范围[16]为：弹性模量E=10～70 GPa，泊松比v=0.15～0.30，单轴抗压强度σc=50～200 MPa，起裂应力与单轴抗压强度σci/σc=0.2～0.6。在PFC2D 中，σci通过出现初始裂纹的应力与峰值应力的比值R设定，本文设定R为1%，即σci等于当裂纹数达到峰值裂纹数的1%时所对应的应力。

图2 细观参数对v的影响Fig.2 Effect of mesoscopic parameters on v

图3 细观参数对E的影响Fig.3 Effect of mesoscopic parameters on E

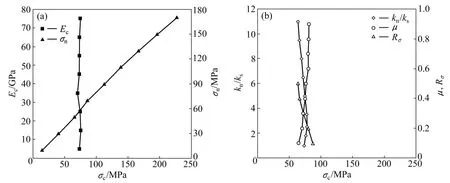
图4 细观参数对σc的影响Fig.4 Effect of mesoscopic parameters on σc

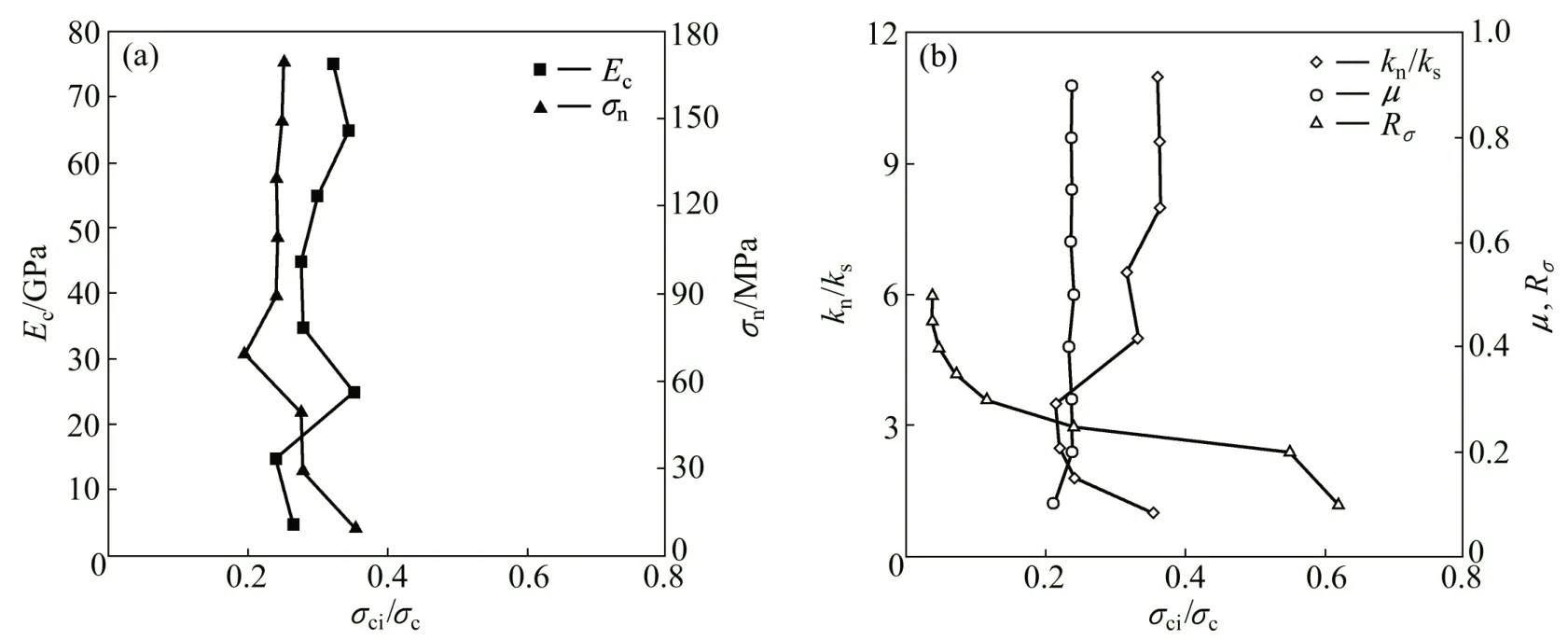
图5 细观参数对σci/σc的影响Fig.5 Effect of mesoscopic parameters on σci/σc

2.3 宏−细观参数关系式

考虑到待定的细观参数有5个，采用5因素球面对称设计表(表1)，5因素X1，X2，X3，X4和X5分别为Ec，kn/ks，σn，μ和Rσ。为确定表1中各因素水平代码对应的值，以因素Ec为例说明，Ec的范围为7～51，则Ec的水平代码，0和所对应的值分别为7，29和51。令X1的水平代码−1和1对应的值分别为x和y(表4)，根据上述比值相等的原则，有

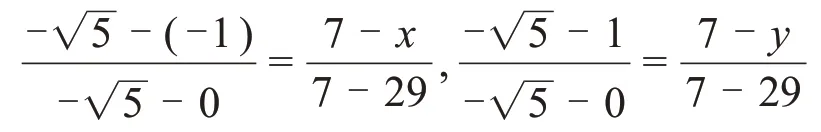
解得x=19.16，y=38.84。同理，可求得其他因素水平代码对应的值，如表5所示。将表5中各因素水平代码对应的值与表1中的值相对照，可得到具体的球面对称设计试验表，如表6所示。

根据球面对称设计试验表(表6)，选取每行中的5个细观参数值，进行PFC2D模拟计算。表7所示为模拟计算43 次试验得到的岩石单轴压缩试件宏观力学参数(E，v，σc和σci/σc)，参数范围为：E=10.16～72.77 GPa，v=0.1603～0.315，σc=49.70～198.98 GPa，σci/σc=0.244～0.674，基本符合岩石的力学参数范围。

表4 因素Ec水平代码对应的值Table 4 Corresponding values for horizontal codes of factor Ec

表5 各因素水平代码对应的值Table 5 Corresponding values for horizontal codes of each factor

表6 球面对称设计试验表Table 6 Spherical symmetric design table

表7 球面对称设计试验模拟结果Table 7 Simulation results of spherical symmetry design test

球面对称设计的试验结果可采用线性或非线性方法拟合[7]，本文采用多元线性回归对表7 中模拟试验结果进行拟合，分别建立4个宏观参数(E，v，σc和σci)与5个细观参数(Ec，kn/ks，σn，μ和Rσ)之间的关系式：

相关系数R2均在90%以上，表明拟合精度较高，能够准确反映岩石宏−细观参数的关联性，其中摩擦因数主要影响峰值后的响应，建议取μ=0.5[9]。式(1)适用于宏观力学参数满足E=10～70 GPa，v=0.15～0.30，σc=50～200 MPa，σci/σc=0.2～0.6的岩石材料。若已知岩石4个宏观参数(E，v，σc和σci)，由式(1)可计算得到4个细观参数。

3 实验验证

3.1 岩石单轴压缩实验

为验证宏−细观参数关系式(1)，选取7 种不同的岩石材料，根据其宏观力学参数(见表8)，分别计算得到PFC2D 细观参数值(Ec，kn/ks，σn和Rσ)，如表9所示。

基于不同岩石材料的PFC2D 细观参数(表9)，采用标准岩石试样(长×宽为50 mm×100 mm)进行单轴压缩模拟计算，得到应力−应变曲线(见图6，以砂岩和BS 花岗岩为例)和宏观力学参数(见表10)，并与试验结果进行对比。由图6 可见：模拟应力−应变模拟曲线(OB′C′D′)可分为弹性(OB′)、损伤(B′C′)和破坏(C′D′)3个阶段，但没有出现类似试验曲线(OABCD)的压密过程(OA)，这是由于在压缩试验的初始阶段，微孔、微裂缝等闭合引起非线性不可逆变形(OE)。计算得到的砂岩弹性模量E(OB′段斜率)和压缩强度σc(峰值点C′应力)分别为34.17 GPa和193.53 MPa，与实测值E=34.68 GPa，σc=190.8 MPa 相比相对误差均较小，均约为2%；同理，计算得到的BS花岗岩E和σc与实测值相对误差均小于2%。当忽略压密阶段、试验曲线ABCD向原点水平左移OE段后，所得曲线与模拟曲线基本重合，两者吻合较好。

表8 不同岩石的宏观力学参数(试验结果)Table 8 Macroscopic mechanical parameters of different rocks(experimental results)

不同岩石试样在单轴压缩下宏观力学参数的模拟结果与试验结果对比见表10。从表10 可见：两者相对误差小于5%，精度较高，表明采用球面对称设计建立的宏−细观关系式(1)计算PFC2D 细观参数的方法是合理的、有效的。

3.2 岩石多裂纹断裂试验

为进一步验证宏−细观参数关系式(1)，模拟含3 条平行裂纹的砂岩试件(长160 mm、宽80 mm、厚30 mm)的单轴压缩断裂试验[17]。如图7所示，试件模型中从上至下依次为预制裂纹1、预制裂纹2、预制裂纹3，预制裂纹长为15 mm，宽为2.5 mm，预制裂纹1 与预制裂纹2和3 内尖端的距离2b=20 mm，垂直于预制裂纹2和3的距离d=10 mm，预制裂纹1的水平夹角α=45°，预制裂纹1和3内尖端连线与水平方向的夹角β=75°，实测的砂岩宏观力学参数和基于关系式(1)计算得到的PFC2D 细观参数见表8和表9。

表9 不同岩石的PFC2D细观参数(计算结果)Table 9 PFC2D microscopic parameters of different rocks(calculated results)

图6 单轴压缩下完整岩石的应力σ−应变ε曲线Fig.6 Stress−strain curves of intact rocks under uniaxial compression

表10 不同岩石的宏观力学参数(模拟与试验结果对比)Table 10 Macroscopic mechanical parameters of different rocks(comparison of simulation and test results)

图7 含3条平行裂纹砂岩试件模型Fig.7 Model of sandstone specimen with three parallel cracks

图8 单轴压缩下含3条平行裂纹的砂岩试件裂纹扩展轨迹(模拟结果)Fig.8 Propagation trajectories of sandstone specimen with three parallel cracks under uniaxial compression(simulation results)

图9 单轴压缩下含3条平行裂纹的砂岩试件裂纹扩展轨迹(试验结果)[17]Fig.9 Propagation trajectories of sandstone specimen with three parallel cracks under uniaxial compression(test results)

在单轴压缩下，含3条平行裂纹的砂岩试件裂纹扩展轨迹其PFC2D 模拟结果和试验结果分别如图8和图9所示。由模拟结果可知：3 条平行裂纹AB，CD和EF均有新裂纹分别从裂尖起裂(图8(a))，沿着轴向加载方向扩展(与含单一斜裂纹的试件扩展形式相同)，其中，浅色和深色分别表示拉应力和剪应力超过平行键法向强度、剪切强度而形成的拉裂纹、剪裂纹，拉裂纹居多，起裂主要受拉应力控制。从图9(a)可见：只有2条平行裂纹AB和CD的尖端先出现新裂纹，这可能是实际岩石材料的非均质性所致。从图8(b)可见；随着荷载增加，裂尖E的新裂纹因到裂纹AB和CD的距离较远，相互影响较小，仍沿原轴向加载方向扩展，而裂尖F的新裂纹逐渐扩展至裂尖C附近区域，最终与裂尖C贯通；裂尖B和裂纹C扩展因受到裂尖D和A的应力强度因子影响而改变方向，最终与裂尖D和A贯通尖端；裂尖A和D新裂纹沿轴向加载方向双向扩展，裂尖A和D逐渐贯通，与图9(b)所示实验结果相符，此时，裂尖A，C和D均有2 条裂纹相互贯通，应力集中得到释放，裂尖B只有1条新裂纹，故产生次生裂纹(图8(c)，9(c))。从图8(d)和图9(d)可见：随着进一步加载，裂尖E的新裂纹逐步向试件上端扩展时受到压密阻碍，又分叉衍生出向下扩展的次生裂纹。但模拟中次生裂纹趋向于与试件右侧边缘贯通，试验中次生裂纹轴向加载方向延伸，其中差异可能是实际岩石材料的非均质性所致。由此可见：在单轴压缩下，含3条平行裂纹的砂岩试件裂纹扩展轨迹其PFC2D 模拟结果与试验结果较吻合，从而验证了采用球面对称设计法标定PFC2D 细观参数的合理性和可靠性。