K型及T型管节点的极限承载力参数分析

雷 婷

(宁夏大学新华学院 宁夏银川 750021)

0 引言

近年来，随着多维数控设备的发展，直接焊接连接的钢管桁架结构被广泛应用于大跨度空间结构中。对于相贯线焊缝，在焊接过程中，由于焊接接头及近焊缝区的母材经历了相当复杂的高温加热及冷却过程，从而使材料特性和损伤累积特性比钢材复杂许多。在实际工程中，焊接节点处的断裂也是钢结构的主要破坏形式，在地震作用下焊缝处及热影响区更敏感，焊缝的破坏对结构的损伤极大，在影响结构承载力性能的同时有可能造成整个结构破坏。近年来，多通过有限元法进行钢管节点的承载力模拟计算。J.C.Paul[1]利用有限元软件计算了XX型圆管节点的承载力，并与X型圆钢管节点做了比较。Vegte[2]在前人有限元研究基础上，用壳体单元模拟焊缝，给出了焊缝壳体单元有限元模型。杨文伟等[3]利用ABAQUS软件对KK型搭接节点的隐藏焊缝是否焊接进行了讨论，得到隐藏焊缝在不焊时节点的滞回性能好于焊时的节点。本文基于前人研究的基础，主要对考虑焊缝的K型及T型钢管节点，通过参数变化，量化分析其对节点承载力的影响，以研究K型及T型钢管节点在不同参数变化下的极限承载力，并给出实际工程中的一些建议。

1 模型参数选取

为方便计算，本文所选几何模型弦杆直径均取200mm，仅对几何参数β，γ、τ进行变化，对K型钢管节点和T型钢管节点各设计了3×3×3=27个模型进行有限元计算。β分别取为0.4、0.7、0.9，γ分别取为10、20、30，τ分别取为0.4、0.7、1.0。另外，对K型节点弦杆与腹杆夹角均取60°，两腹杆的几何尺寸取相同数值，贯通腹杆受压，内隐藏焊缝不焊。

2 建立有限元分析模型

本次数值模拟分析，选用ANSYS有限元软件单元类型库中三维四节点弹塑性壳单元Shell181。Shell181单元适用于分析非线性的大变形试件，尤其是在采用其他单元不收敛时使用该单元则更容易收敛。焊缝的模拟均为沿腹杆与弦杆的全周角焊缝，焊缝单元宽度参数hw=t，焊缝单元高度参数hh=0.5T+t，焊缝壳体厚度取为0.5t，K型和T型钢管节点焊缝单元有限元模型如图1所示。

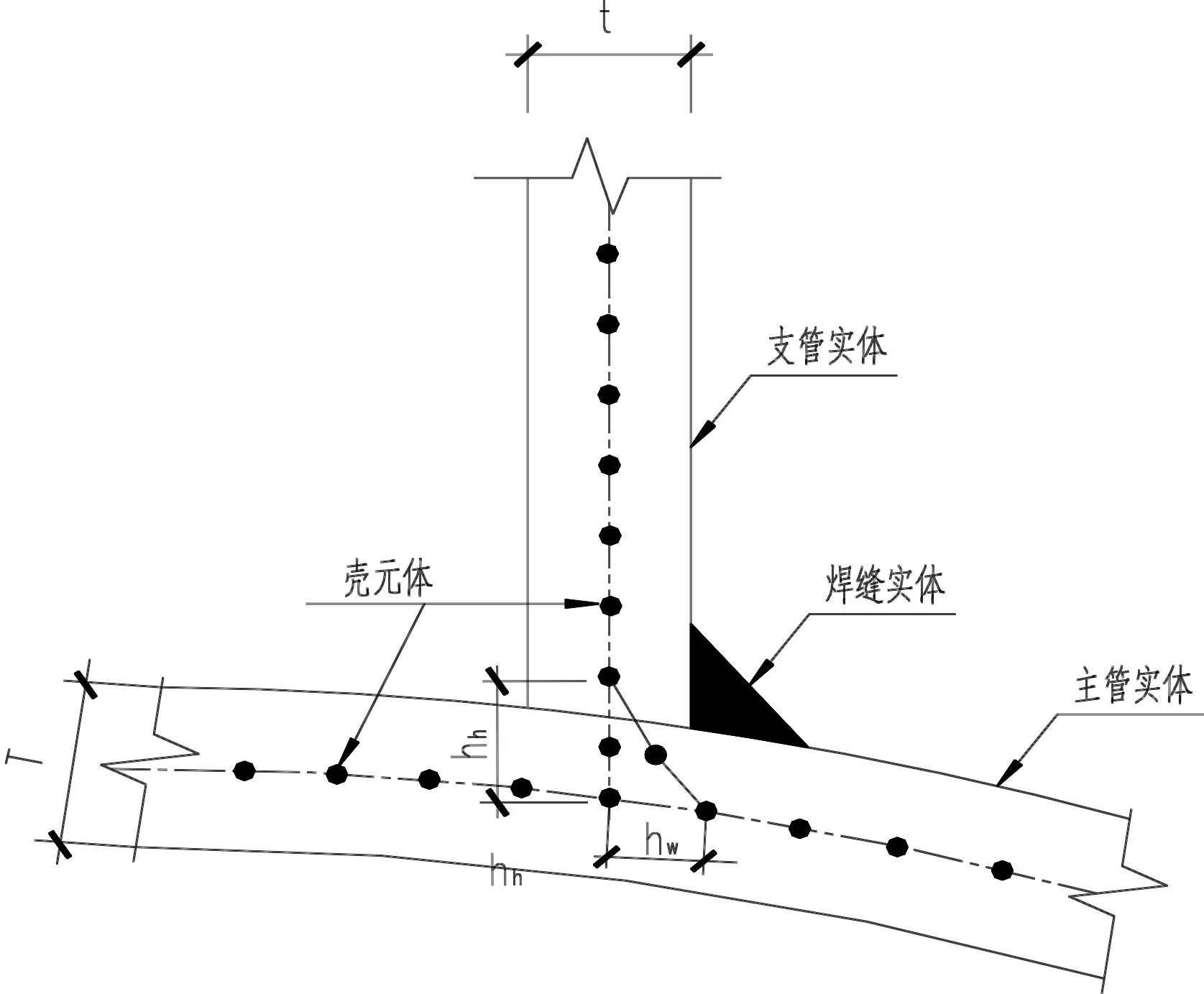
图1 焊缝单元有限元模型

对钢管节点的网格划分考虑了网格的均匀过渡，划分时先对模型进行分区，用自由网格划分和映射网格划分相结合的方法，如图2所示。对于焊接模型，因弦杆、腹杆交界处应力集中严重，是分析重点，因此采用自由网格划分且网格划分较密；远离相贯线处，采用映射网格划分且划分渐变稀疏，便能达到此处要求的计算精度，从而提高计算效率。最后，根据ANSYS的误差信息，判断网格划分是否满足要求。

边界条件、加载方式及极限承载力的确定均与文献[4-6]相同，如图3所示。即：K型节点边界条件和加载方式为弦杆一端按固定支座考虑，另外一端为仅有沿杆轴线方向位移的固定支座。两腹杆端部仅允许沿管轴线方向有位移，径向位移被约束；在拉压腹杆端部截面中所有节点上施加沿腹杆轴向的集中荷载。

T型节点试验中节点弦管边界均为铰接，有限元模型相应约束弦管端部节点Y、Z向平动自由度，放松X向平动自由度及旋转自由度。为保证轴向加载，约束支管端部X、Z向平动自由度，同时为防止弦管发生沿X向的平动而不能保持支管的轴向受力状态，将弦管中央顶部节点与支管端部节点的X、Z向平动自由度耦合。支管轴向荷载通过支管端部四节点对称施加。

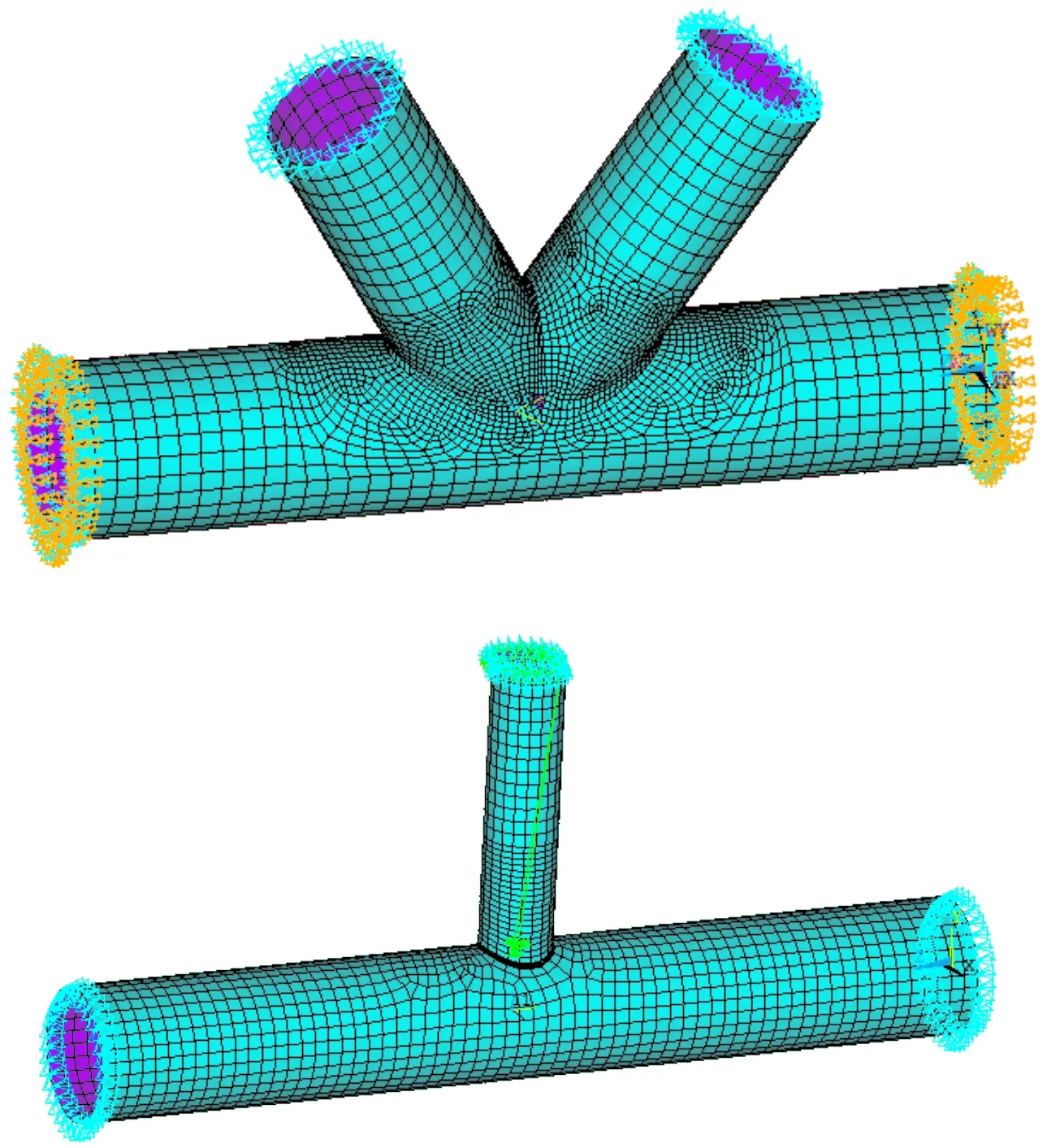
图2 节点单元模型

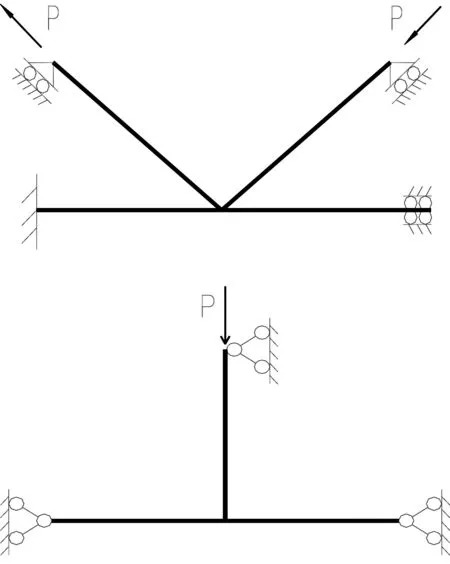
图3 边界条件和加载方式

研究表明，当采用Newton-Raphson方法进行非线性迭代求解时，刚度矩阵可能会变成奇异矩阵。而弧长法可以使得Newton-Raphson平衡迭代沿一条弧收敛到其平衡路径，从而帮助稳定求解。因此，本文采用基于弧长控制的Newton-Raphson方法求解，在出现负刚度时终止分析。使用此法需要关闭自动时间步、线性搜索和DOF结果预测选项。

本文极限承载力判定采用Lu的方法，即：对于荷载位移曲线有极值点的情况，如果对应的变形小于3%D，则以该极值为极限承载力；反之，则以变形为3%D的荷载为极限承载力。对于荷载位移曲线无极值点的情况，统一以变形为3%D的荷载为极限承载力。

3 K型钢管节点几何参数对极限承载力的影响

β的影响：由图4可知，当其他参数不变时，节点的极限承载力随β值的增大线性增加。其中对γ=10的节点承载力增幅最多，β值的增加导致腹杆截面面积增加，使承载力大幅提升。而对于γ=30的节点增加的幅度最少，β值的提高虽然增大了腹杆的截面面积，但使腹杆产生局部屈曲的概率加大，所以增加的幅度不显著。在工程实际中，建议使拉压腹杆直径和壁厚搭配合适。

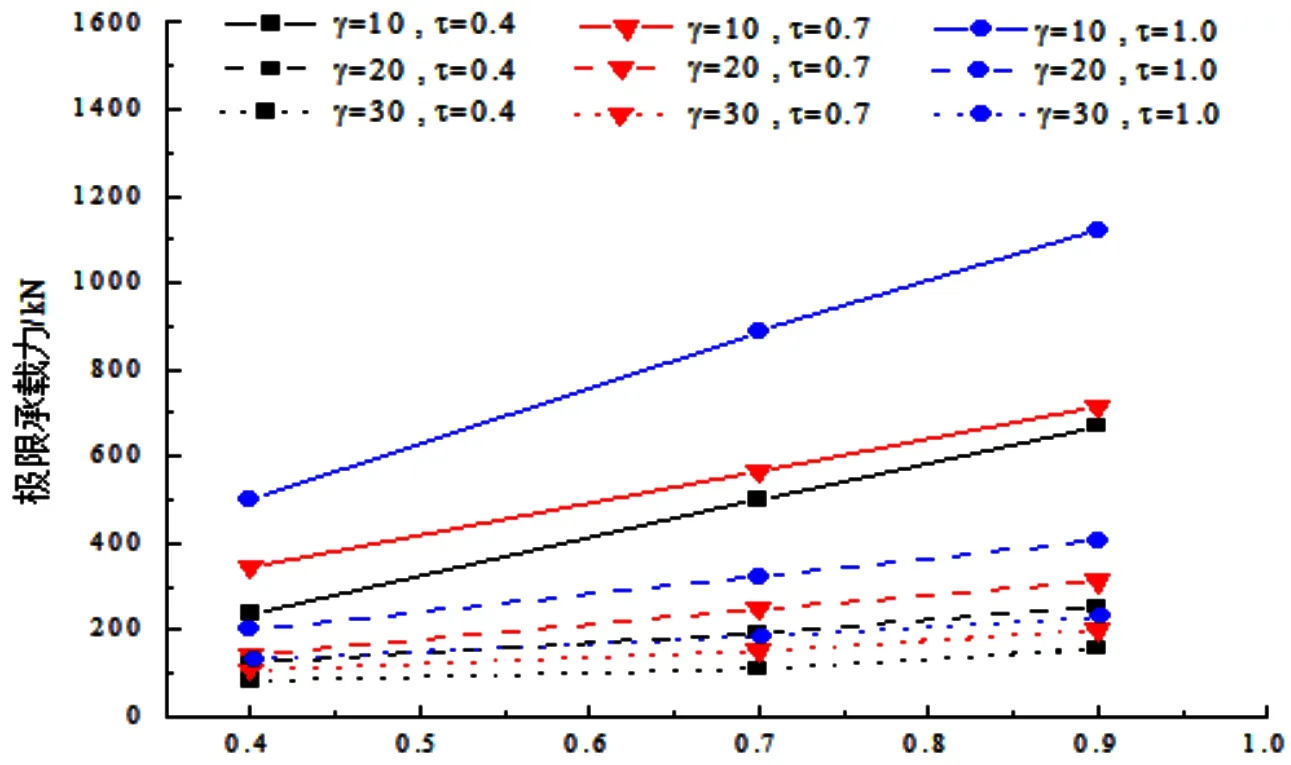
图4 K型节点极限承载力与β值的关系

γ的影响：由图5可知，当其他参数不变时，节点的极限承载力随γ值的增大而减少。因为γ值增加相当于弦杆壁厚减少，使弦杆抗弯能力减弱，从而减少了节点的极限承载力。10<γ<20时，节点的承载力减小的比较快，而20<γ<30时，节点的承载力减少的比较慢。此外，当0.7<β<0.9时，其承载力随γ值降低的幅度高于β=0.4的节点。

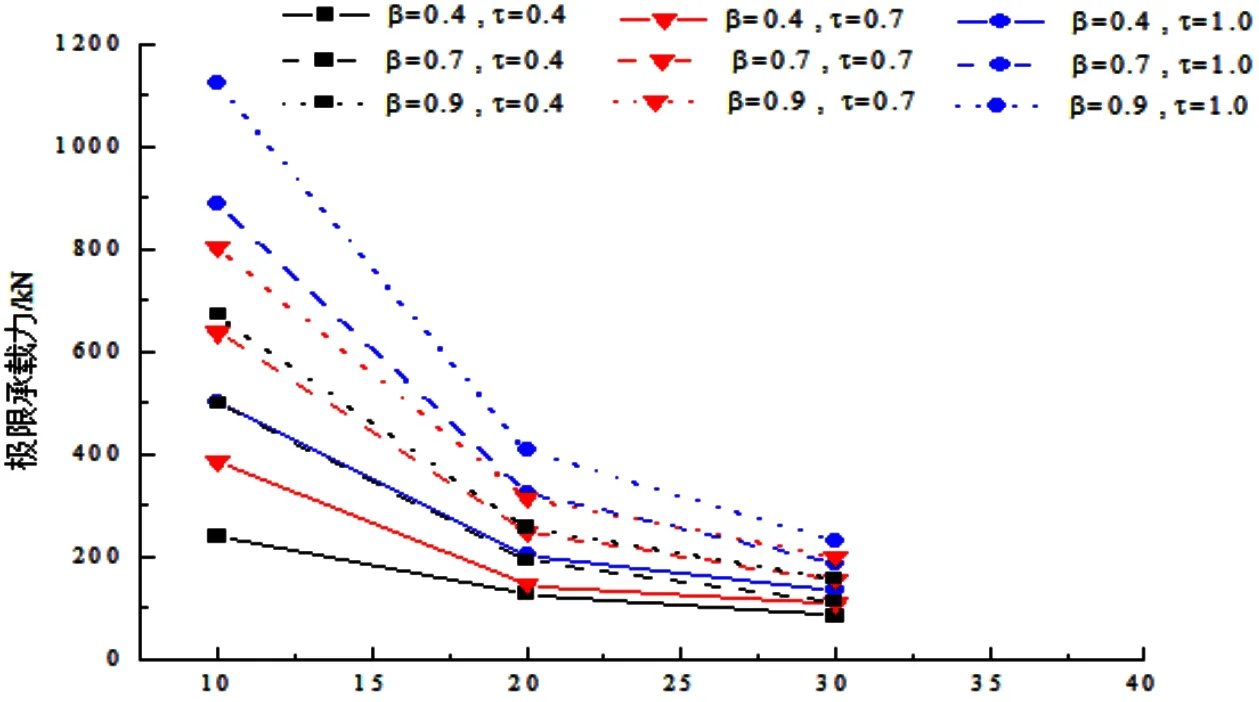
图5 K型节点极限承载力与γ值的关系

τ的影响：由图6可知，当其他参数不变时，随着τ值的增大节点极限承载力随之增大，主要因为τ值的增大提高了腹杆抵抗局部屈服的能力。

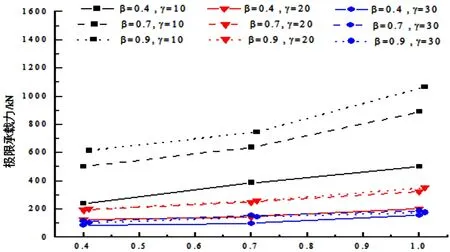
图6 K型节点极限承载力与τ值的关系

4 T型钢管节点的几何参数对极限承载力的影响

β的影响：由图7可知，当β值增大时，节点的极限承载力随之增大，当β>0.7，γ=10时极限承载力增加的幅度较多，而γ=30的节点增加的幅度较少。

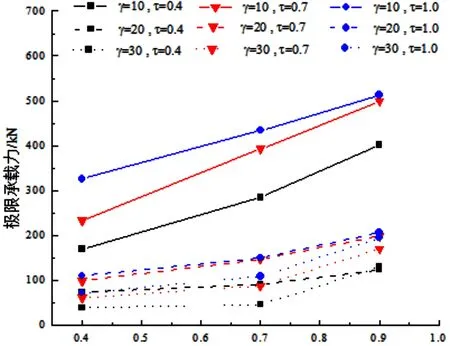
图7 T型节点极限承载力与β值的关系

γ的影响：由图8可知，当γ值增大时，对腹杆的约束能力越弱，节点的极限承载力越小。10<γ<20时极限承载力减少得较快，而20<γ<30时，节点承载力减少得较慢。

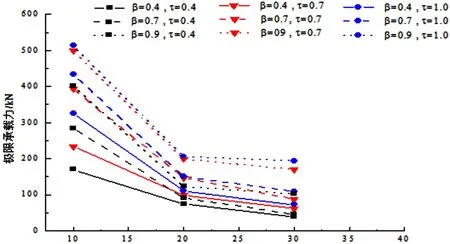
图8 T型节点极限承载力与γ值的关系曲线

τ的影响：由图9可知，τ值对节点的极限承载力的影响不是特别大，由此可知，T型节点的极限承载力与主支管壁厚比的关系不大，在满足承载力的前提下，可适当减少腹杆的厚度。

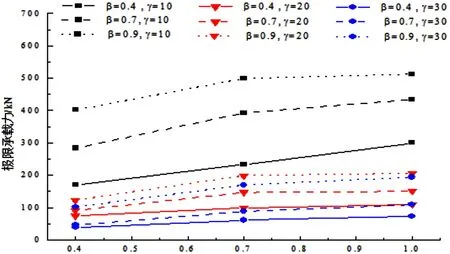
图9 T型节点极限承载力与τ值的关系曲线

5 结论

(1)本文建立K型及T型钢管节点考虑焊缝的有限元模型，所得结果与试验数据吻合良好，可作为有限元分析依据。

(2)对K型节点，弦杆与腹杆的夹角θ不变时，节点极限承载力与β、γ及τ值有关。当β值、τ值增大时，节点的极限承载力增大，但是当γ值增大时节点的极限承载力减少。在工程实际中，建议使拉压腹杆直径和壁厚搭配合适。

(3)对T型节点，当β值增大而γ值减少时，节点的极限承载力增大。但是τ值对节点的极限承载力影响不是特别大，在满足承载力的前提下，可适当减少腹杆的厚度。