论数学教学中如何体会图形运动思想并领悟其中独特妙用

◆李春燕

(山东省滨州市滨城区第四中学)

数学思想方法是数学中的精髓，是联系数学中各类知识的纽带.掌握这些思想方法，将使人终身受益.图形运动的思想在初中数学中，一般指图形的平移、对称、和旋转三种.对称包括轴对称和中心对称.在操作中，轴对称常以翻折形式出现，中心对称是旋转角为180°时的旋转运动.点的运动问题也体现了图形运动的思想.

首先要熟悉各类图形运动后产生的性质.运动后的图形与原图形是全等形；平移后的图形与原图形对应线段平行且相等，原图形上的每一点都沿同一方向移动了同一距离；若两个图形关于某直线成轴对称，则这两个图形上对应点的连结线段被对称轴垂直平分，对应线段或互相平行或它们所在直线的交点必在对称轴上；若两个图形关于某点成中心对称，则这两个图形上对应线段互相平行且相等，对应点连结的线段都通过对称中心，且被对称中心平分；旋转运动中，注意旋转中心，旋转方向和旋转角.

解几何题时，由于条件分散，相关图形又不集中，很难发现量与量之间的关系，此时，将图形进行平移、对称、旋转变换，将分散的条件集中起来，或置于某一熟悉的图形之中，以改变问题情景，发现和运用某些特征、性质或联系，由此找到问题的突破口和解决问题的关键，从而使原有问题得到解决.

这类问题的解题关键在于如何“化动为静”，“以静制动”，如何化繁为简，化分散为集中，化难为易，体现“以不变应万变”的核心规律.以下通过实例来渗透，理解，把握，体会，进而达到举一反三，熟练运用.

例1：如图，梯形ABCD中，AD∥BC，且∠C=90°-1/2∠B.求证:AB=BC-AD.

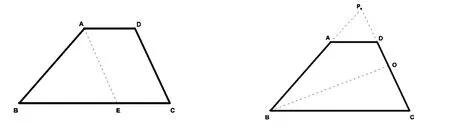
简解：1.利用平移.将线段DC沿DA方向平移到AE，其中点E在边BC上.则AECD为平行四边形，∠DAC=∠AEB=∠C，AD=EC.又∠C=90°-1/2∠B，∴2∠C+∠B =180°，又∵∠DAB+∠B==180°∴∠BAE+∠EAD+∠B=∠BAE+∠C+∠B=180°，∴∠BAE=∠C=∠AEB，∴AB=BE=BC-EC=BC-AD.

2.常规解法.延长BA交CD的延长线于点P.过点B作CD边的垂线，垂足为点O.利用已知条件证得△BPC与△APD皆为等腰三角形，进而证得结论.

点评：比较两种证法，前者利用平移变换，将已知条件集中一个三角形中，到化繁为简，求解十分方便，体现了运动思想解题的优越性;而第二种解法过程较复杂，烦琐.

变式训练：如图，线段01O2与线段AB相交于点P，且01A⊥AB，O2B⊥AB，已知01A=r，O2B=R，01O2=d，(R、r、d均为常数).试求线段AB的长.

提示:利用平移，将AB平移到O1B1，将已知量R、r、d都集中在Rt△01O2B中，易求得AB即O1B1的长.(而利用平行线分线段成比例定理和方程思想，求得O1P、O2P的长，再利用勾股定理求得AP、BP的长，进而求得AB的长却很烦琐.)

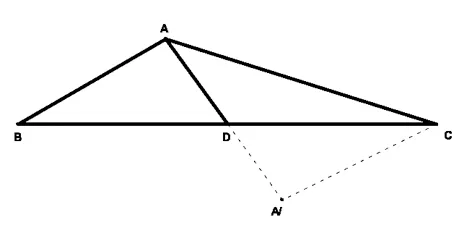
例2：如图，△ABC中，BC的垂直平分线交∠BAC的外角平分线于点D，连结DC 、DB.求证:∠DBA=∠DCA.

简解:将△BAD沿AD翻折到△B1AD，∵DA平分∠BAC的外角，∴AB1线在CA的延长线上，∴△ABD≌△AB1D，∴BD=B1D，且∠DBA=∠D B1A

∵DE垂直平分BC，∴DC=DB，∴DC=DB1，∴∠D B1A=∠DCA.因此，∠DBA=∠DCA.

点评：此题直接证∠DBA=∠DCA非常困难，而通过翻折(周对称运动)，使∠DBA=∠D B1A，且∠DB1A与∠DCA在同一个三角形中，又是等腰三角形，因而得到∠DBA=∠DCA.本题通过运用图形运动思想，找准问题的切入点，化难为易，妙笔生花，殊途同归，不失为一典范好例.遇中点或中线考虑，作轴对称图形，也是常用辅助线之一.

变式训练：已知:△ABC中，AB=AC，∠BAC=120°，BD平分∠ABC，且与AC交于点D.求：AD:DC的值.

提示：将△ABC沿BD翻折，使点A落在BC边上A1点，此时△DA1C是直角三角形.运用30°角对的直角边是斜边的一半，进而得出结论.

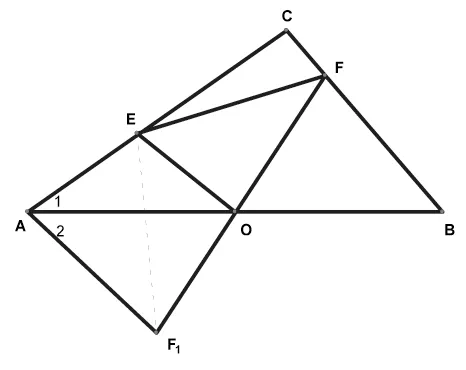
例3：如图，△ABC中，∠C=90°，O是AB的中点，将三角尺的直角顶点置于点O，并绕点旋转，使直角尺的另一边交边AC于E，直角尺的另一边交边BC于F(E、F均不与A、C、B重合)，连结EF.试问：三条线段AE、EF、FB是否总能构成一个直角三角形？请做出判断，并证明你的结论.

简解：三条线段AE、EF 、FB总能构成一个直角三角形，且EF是斜边，最长边.将△BOF绕点O旋转180°至△AOF1，(即作出△BOF关于O点的中心对称图形△AOF1)，连结AF1，∵AF1=BF，∠2=∠B，∠ACB=90°，∴∠1+∠2=90°.即∠EAF=90°.∵EO⊥FF1，且F1O=FO，∴EF1=EF.

又△AEF1是直角三角形，有AE2+AF12=EF12，即AE2+BF2=EF2，∴AE、EF、FB总能构成一个直角三角形，且EF是斜边，最长边.

点评:此题是一结论开放性题，由于三线段AE、EF、FB较分散，通过图形的中心对称运动，使它们集中于一个AEF1中，而此三角形恰好是直角三角形，从而证明AE、EF、FB总能构成一个直角三角形，且EF是斜边，最长边.由此看来，将分散条件集中，是图形运动思想在解题中的独特妙用.

变式训练：已知:△ABC中，AD是BC边上中线，且AD⊥AB，AC=10，AD=4.求:边BC的长.

提示：作△ABD关于点D的中心对称图形△A1CD，则△AA1C是直角三角形，由勾股定理得A1C=6，再由Rt△A1CD，求得DC，最后得BC=2DC.进而求得结果.

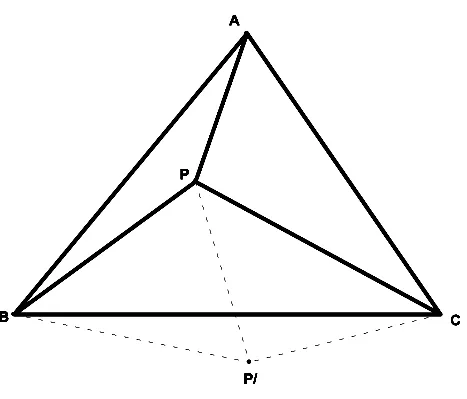
例4：已知点P是等边三角形ABC内一点，∠APB=150°，PA=3，PB=4.求PC的长.

简解：将△APB绕点B顺时针旋转60度，连结P P′.

因△ABC是等边三角形，故△APB与△CP′B全等.BP=B P′，∠PB P′=60°.则得△PB P′为等边三角形，BP′=BP=4，P′C=PA=3.

∴∠PB P′=60°，P′P= BP=4.又∵∠APB=150°∴∠P P′C=90°.在Rt△PP′C中，由勾股定理得PC=5.

点评:此题所求线段PC与已知线段PA、PB构不成一个三角形，条件分散，不易求解.由于△ABC是等边三角形，具备旋转角60°的旋转条件，因此可作旋转运动，将已知条件集中到一个直角三角形中，便于求解.此题解法新颖，充满魅力.

变式训练1：如图，Rt△ABC中，∠ABC=90°，AB=3，BC=5，

以AC为边向△ABC外作正方形ACEF，设O为正方形ACEF的中心，连结BO.求BO的长.

提示：连结AO、CO.将△OAB绕点O逆时针旋转90°到△OCB1，可证∠OC B1=∠OAB，点B、C、B1共线，进而证得△OBB1是等腰直角三角形，再求得BO长.

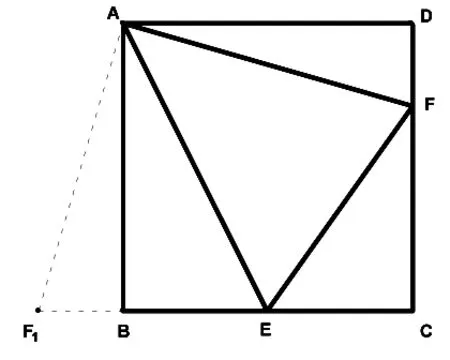
提示：将△ADF绕点A顺时针旋转90°到△ABF1，可证△AEF≌△AEF1，∠AEF=∠AEF1=60°进而求的EC、EF、EF1.将△AEF的面积转化为△AE F1的面积.可为构思独特.

将图形运动的数学思想运用于数学实际，利用平移、对称、和旋转变换，寻求变化过程中的不变因素，抓住变换特征，研究内在联系，找准突破口，将条件集中，数形结合，化难为易，化繁为简，建立数量关系，就能达到动静结合，以不变应万变的核心目的.更会提升思维的高度，发展创新能力.