基于ANFIS的RPC中钢筋搭接性能预测

陈潇， 方志， 陈佳醒

(湖南大学 土木工程学院, 湖南 长沙 410082)

1 前言

活性粉末混凝土(Reactive Powder Concrete，简称RPC)系基于最大密实度原理配制的一种超高性能混凝土，通过提高其组分的细度与活性、减少内部缺陷，以获得由其组分材料所决定的最大承载力及优异的耐久性。与普通混凝土相比，RPC具有超高的抗压强度和较高的抗拉强度、良好的韧性、优异的耐久性、热养护后基本无收缩且徐变大幅降低等特征，RPC也由此被归于超高性能混凝土范畴并被视为新一代水泥基材料，在土木工程中具有良好的应用前景。有关RPC材料的国家标准GB/T 31387-2015《活性粉末混凝土》已颁布实施，但目前中国国内尚无相应结构设计方面的国家规范。

配筋混凝土结构中钢筋的连接接长不可避免，一般有搭接、焊接和机械连接等连接方式，且以搭接连接最为简便。搭接连接通过搭接区域的混凝土来实现钢筋之间的应力传递。目前对于普通混凝土中钢筋搭接连接性能的研究较为充分。徐有邻等通过32个钢筋搭接对拉试验和8个钢筋搭接梁受弯试验，研究了搭接传力性能及其影响因素，提出了搭接强度和钢筋搭接长度计算公式，并被现行的GB 50010-2010《混凝土结构设计规范》所采用；赵培完成了123个约束浆锚搭接连接试件的对拉试验，获得了螺旋箍筋配箍率对钢筋搭接长度的影响规律；Mehmet Karatas等通过不同硅灰含量自密实混凝土梁和普通混凝土梁的受弯试验，研究了硅灰含量对搭接性能的影响。

国内外对RPC中钢筋搭接连接性能的研究尚才开始。Lee基于10个采用搭接钢筋配筋的超高强度混凝土梁的受弯试验，研究了不同搭接长度对搭接性能的影响，结果显示：在钢纤维体积掺量为2%、强度等级为130 MPa的超高强度混凝土中，130 mm搭接长度对于13 mm直径钢筋的搭接连接足够可靠；Choi等完成了12个复合纤维增强超高性能混凝土中钢筋搭接对拉试验，结果表明：在强度等级为100 MPa的超高性能混凝土中，140 mm搭接长度可为直径为16 mm钢筋提供可靠的传力搭接。

总之，目前国内外有关RPC中钢筋搭接连接性能的研究才刚起步，RPC强度和配箍率等参数对搭接性能影响规律的研究尚未涉及，限制了RPC这种超高性能水泥基材料的工程应用。

自适应神经模糊推理系统(Adaptive Network based Fuzzy Inference System，简称ANFIS)，是模糊推理系统与神经网络相结合的产物，既继承了传统神经网络自适应性以及学习能力强等方面的优点，又克服了传统神经网络存在的局部极小值等缺陷，因而在土木工程中得到了较为广泛的应用。

搭接应力-滑移曲线是对搭接连接性能的综合反映。为了确定RPC中搭接钢筋在对拉荷载下的连接性能，该文以搭接长度、RPC强度和配箍率为试验参数，对13个RPC中钢筋搭接连接试件进行对拉试验，得到各试件的搭接应力-滑移曲线，并以试验结果为样本，建立基于ANFIS的RPC中钢筋搭接应力-滑移曲线模型。以期通过该模型预测不同搭接长度、RPC强度和配箍率下RPC中钢筋搭接试件的搭接应力-滑移曲线，为RPC中钢筋搭接的有限元分析和工程设计提供依据。

2 试验概况

2.1 试件设计

设计制作了13个RPC中的钢筋搭接试件，试验的主要参数为搭接长度、RPC强度和配箍率。试件RPC块体部分的截面尺寸为150 mm×150 mm，长度即为搭接长度，分别取100、150和200 mm；RPC强度分别为100、120和150 MPa；搭接钢筋采用强度等级为HRB400、直径为20 mm的带肋钢筋；箍筋采用强度等级为HRB335、直径分别为6、4 mm的带肋钢筋，对所有配箍试件，箍筋间距均保持为50 mm，搭接长度100、150和200 mm试件内的箍筋个数分别为2、3和4个，同一搭接长度试件内的配箍率分别为0、0.34%和0.75%；试件内的架立筋采用强度等级为HRB335、直径为6 mm的带肋钢筋。试件尺寸及配筋构造见图1。

图1 试件尺寸及配筋构造(单位：mm)

试件编号及主要参数见表1。编号中L、R和S及其后的数字分别表示搭接长度、RPC强度和配箍率，如试件编号L100-R100-S34表示试件的搭接长度为100 mm、RPC强度为100 MPa、配箍率为0.34%。

表1 试件参数及主要试验结果

注：表中L为搭接长度；fcu为RPC立方体抗压强度；ρv为配箍率；Fu为极限荷载；τu为与Fu对应的搭接应力；τau为ANFIS模型得到的搭接强度；破坏模式中：P为钢筋拔出破坏，B为钢筋拉断破坏，Y表示钢筋屈服。

2.2 材料力学性能

所用钢筋力学性能的测试结果如表2所示。

RPC的配合比(质量比)及实测强度见表3，其中钢纤维体积掺量为2%，RPC的强度为边长100 mm立方体28 d的实测抗压强度。

2.3 加载方式与测点布置

采用单向拉伸的方法进行钢筋搭接性能试验，加载在专门加工制作的反力架上进行，加载设备采用500 kN穿心式液压千斤顶。采用压力传感器控制荷载大小，主要测点布置如图2所示。在两根搭接钢筋的加载端和自由端均布置百分表，用于测量搭接钢筋滑移量，获取搭接应力-滑移曲线。

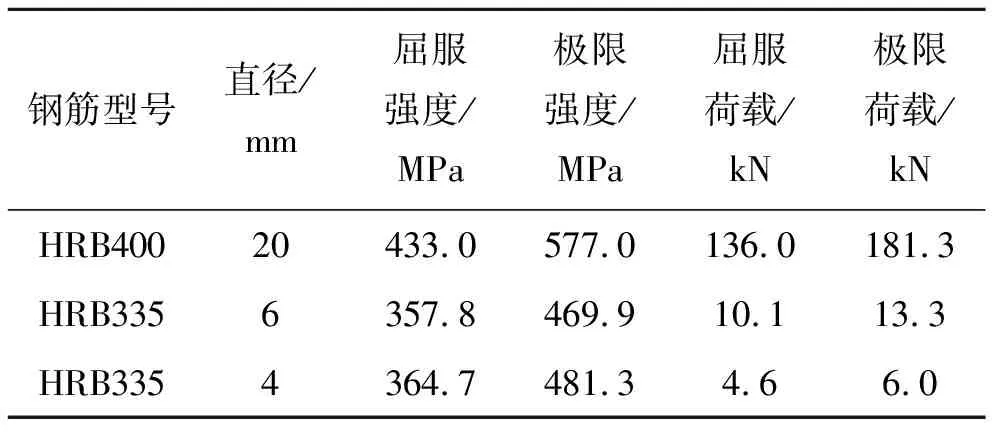
表2 钢筋力学性能

表3 RPC配合比及抗压强度

试验采用分级加载。极限荷载前采用力控制，每级荷载增量约为10 kN，达到极限荷载后采用位移控制，每级位移增量根据滑移发展情况取0.5～1 mm，直至加载钢筋自由端位移超过15 mm左右为止。

3 试验结果

定义试件受力过程中经历的最大荷载为极限荷载，与极限荷载对应的加载钢筋自由端滑移为极限滑移。根据试验量测的荷载值F及搭接长度L，采用式(1)计算搭接区钢筋表面的平均黏结应力(或称搭接应力)。

(1)

图2 加载装置及测点布置

式中：F为对拉荷载；d为钢筋直径；L为搭接长度。

主要试验结果见表1，RPC中钢筋的搭接强度为15.56～21.39 MPa。

试验中出现了搭接钢筋拔出破坏和拉断两种破坏模式。

搭接长度为100、150 mm的试件均发生钢筋拔出破坏，其搭接应力-滑移曲线如图3所示。

图3 钢筋拔出破坏试件的搭接应力-滑移曲线

由图3可知：发生钢筋拔出破坏试件的搭接应力-滑移曲线包含上升段、下降段和残余段。上升段表明：加载之初搭接钢筋与RPC的胶结破坏和滑脱尚未渗透到搭接全长，相对滑移S很小，随着荷载的增大，搭接钢筋与RPC的胶结面被破坏，荷载由摩阻和咬合承担，滑移增长加快，曲线呈现非线性特征；下降段表明：承载力达到峰值后，迅速减小，滑移大幅度增长；残余段表明：滑移发展至一个横肋间距时(直径为20 mm的带肋钢筋横肋间距为10 mm)进入残余段，承载力由RPC与钢筋的摩阻力维持。搭接长度为100 mm与搭接长度为150 mm试件的搭接应力-滑移曲线上升段基本一致，残余段接近平行，形态相近。

搭接长度为200 mm的试件均发生钢筋拉断破坏。试件发生钢筋拉断破坏时搭接钢筋自由端滑移值较小，搭接应力-滑移曲线如图4所示，仅包含上升段。

图4 钢筋拉断破坏试件的搭接应力-滑移曲线

由图4可知：加载初期RPC与钢筋表面的胶结力尚未破坏时，钢筋未发生明显滑移；随着荷载的增大，滑移缓慢增加，直至钢筋被拉断。极限荷载由钢筋的抗拉强度所决定。

4 ANFIS基本原理及结构

自适应网络模糊推理系统，也称为基于网络的自适应模糊推理系统(Adaptive Network-based Fuzzy Inference System，简称ANFIS)。ANFIS是将神经网络与模糊推理系统结合在一起，并基于自适应的建模方法建立起来的模糊推理系统。

ANFIS结构有5层，如图5所示，为简单起见，假定所考虑的模糊推理系统有两个输入x和y，输出为f，用Oi,j表示第i层第j个节点的输出值。各层的功能如下：

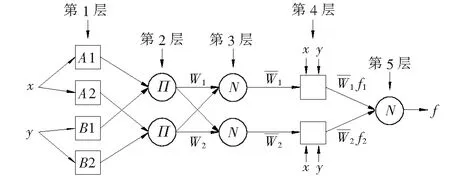
图5 ANFIS结构图

第1层为输入层：

(2)

式中：O1,j表示第1层第j个结点的输出；x，y为各结点的输入；uAj、uBj分别为描述输入量x、y的隶属度函数。

第2层的每个结点为以Π表示的固定结点，将本层输入信号相乘并输出：

O2,j=wj=uAj(x)×uBj(y)，j=1,2

(3)

第3层的每个结点为以N表示的固定结点，其输出为第j条输入与本层所有输入之和的比值：

(4)

第4层中的每个结点均是一个有结点函数的自适应结点：

(5)

第5层为标以∑的固定单结点，其功能在于将本层输入求和并输出：

(6)

5 基于ANFIS的搭接应力-滑移曲线模型

5.1 ANFIS模型的建立

通过Matlab中模糊逻辑工具箱完成RPC中钢筋搭接应力-滑移曲线建模。考虑搭接长度、RPC强度和配箍率3个参数对RPC中钢筋搭接应力-滑移曲线的影响。因此模型的输入变量有4个：搭接长度、RPC强度、配箍率和滑移值。模型的训练结构为网格分类法，输入变量搭接长度、RPC强度、配箍率和滑移值分别赋予2、2、3、5个隶属度函数，其类型均为双S型，输出搭接应力的函数类型设置为线性函数；模型的学习算法设置为混合学习算法。具体结构见图6。

图6 搭接应力-滑移曲线模型的ANFIS结构图

5.2 ANFIS模型与试验结果对比

将10个试件的试验数据进行模型训练，在模型训练完成后，对其余3个试件L100-R120-S34、L100-R120-S75和L150-100-S34的搭接应力-滑移曲线进行检验，并与试验结果对比，以验证模型的适用性。模型的训练和对比情况如表1和图7所示。

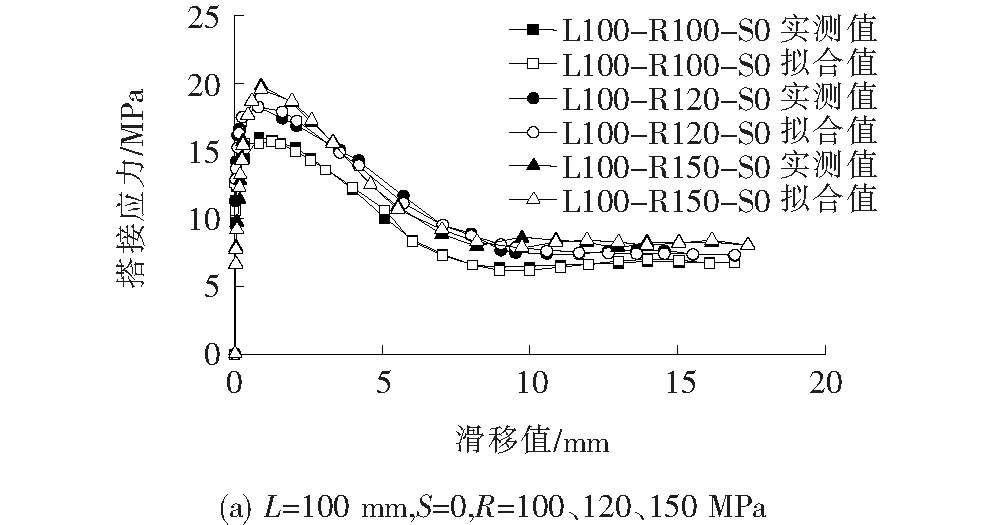
图7 ANFIS模型结果与试验结果对比

由表1 及图7可知:① RPC中钢筋搭接应力-滑移曲线模型对不同参数下各试件的搭接强度拟合和预测效果良好。② RPC中钢筋搭接应力-滑移曲线模型对不同参数下各试件的搭接应力-滑移曲线拟合效果良好。经检验，RPC中钢筋搭接应力-滑移曲线模型对试件L100-R120-S34、L100-R120-S75和L150-R100-S34搭接应力-滑移曲线预测较准确，即该文所提出的基于ANFIS的RPC中钢筋搭接应力-滑移曲线模型可以较好地描述RPC中钢筋的搭接性能。

5.3 搭接性能的参数分析

利用得到的ANFIS模型对不同搭接长度、RPC强度和配箍率下RPC中钢筋搭接试件的试验结果进行预测，并分析各参数对搭接性能的影响。

5.3.1 搭接长度的影响

ANFIS模型预测的不同搭接长度对搭接应力-滑移曲线的影响如图8所示。

图8 不同搭接长度试件的搭接应力-滑移曲线

由图8可知:试件L75-R100-S34、L125-R100-S34发生钢筋拔出破坏，而试件L200-R100-S34发生钢筋拉断破坏。对于发生拔出破坏的试件，当搭接长度由75 mm增加至125 mm时，搭接强度降低3.6%。

5.3.2 RPC强度的影响

ANFIS模型预测的不同RPC强度对搭接应力-滑移曲线的影响如图9所示。

图9 不同RPC强度试件的搭接应力-滑移曲线

由图9可知:与RPC强度为100 MPa的试件相比，强度为150 MPa和200 MPa试件的极限搭接强度分别提高24.1%和42.7%。

5.3.3 配箍率的影响

ANFIS模型预测的不同配箍率对搭接应力-滑移曲线的影响如图10所示。L100-R100-S0、L100-R100-S50和L100-R100-S100分别表示配箍率为0%、0.5%和1%且搭接长度为100 mm、RPC强度为100 MPa的试件。由图10可知:与配箍率为0的试件相比，配箍率为0.5%和1%试件的极限荷载和搭接强度分别提高5.2%和8.3%。

图10 不同配箍率试件的搭接应力-滑移曲线

6 结论

(1) 通过对13个RPC中钢筋搭接连接试件进行对拉试验，结果表明：在对拉荷载下，RPC中钢筋搭接连接分别出现钢筋拔出和拉断两种破坏模式；RPC中钢筋的搭接强度为15.56～21.39 MPa。

(2) 通过试验所得的搭接应力-滑移曲线，建立了基于ANFIS的RPC中钢筋搭接应力-滑移曲线模型，该模型综合考虑了搭接长度、RPC强度和配箍率对搭接性能的影响。通过所得模型拟合和检验的搭接应力滑移曲线与试验结果对比，结果表明：该文所提出的基于ANFIS的RPC中钢筋搭接应力-滑移曲线模型可以较好地描述RPC中钢筋的搭接性能。

(3) 利用得到的ANFIS模型对不同搭接长度、RPC强度和配箍率下RPC中钢筋搭接试件的试验结果进行预测，并分析各参数对搭接性能的影响。结果表明：搭接强度随RPC强度、配箍率的增加而增加，随搭接长度的增加而降低。

(4) 根据试验结果和ANFIS预测模型可知，在强度等级为100 MPa、配箍率为0.34%的RPC中，直径为20 mm带肋钢筋的临界搭接长度约为10倍钢筋直径。