基于模型预测控制和干扰观测器的电子节气门控制
2019-04-16李世华
朱 科,李世华,孙 昊
(东南大学自动化学院,南京 210096)
0 引言
在电子节气门控制系统中,由于非线性和扰动等不确定性的存在使得传统的比例积分控制难以满足高性能控制的要求,因此很多研究者提出了先进的控制算法应用于电子节气门控制系统,主要包括自适应控制[1-2]、滑模控制[3-4]、神经网络控制[5]及模糊控制[6]等.上述方法虽然能在不同方面提高电子节气门控制性能,但是都未从实现某一性能优化指标的角度出发.Vašak等[7]通过线性二次型最优控制方案改善了控制器的动态响应速度,但并未考虑干扰的影响.而在电子节气门系统中,一方面系统会受节气门参数变化及摩擦非线性等不确定性[8]的影响,另一方面电子节气门也会受到发动机抖动和气流冲击等众多外部干扰的影响. 模型预测控制[9](model predictive control,MPC)作为一种新型优化控制算法,通过一段时间内某一性能指标最优来确定未来控制作用,目前已被广泛应用于电机[10]和飞行器[11]等的设计.然而,模型预测控制仅依靠反馈校正并不足以抵抗强干扰,故本文拟通过干扰观测器(disturbance observer,DOB)对扰动进行估算,以期有效抑制扰动,提出一种基于模型预测控制的电子节气门控制算法.
1 电子节气门建模
电子节气门体主要由直流电机、传动齿轮组、阀片、回位弹簧和位置传感器等组成,其结构如图1所示.当驾驶员踩踏加速踏板时,电子计算单元会计算节气门最佳开度,并与节气门当前角度相比较,通过微控制器产生控制电压,Chopper变换器根据控制电压输出电机脉宽调制信号至直流电机,直流电机带动齿轮组转动调节节气门阀片角度到目标开度.同时,节气门位置传感器实时反馈阀片位置信息至控制器,以调整控制输出.

1.微控制器;2.汽车电源;3.Chopper变换器;4.直流电机;5.齿轮箱;6.阀片;7.回位弹簧;8.节气门位置传感器;9.进气气流.图1 电子节气门结构原理图Fig.1 Structural schematic diagram of electronic throttle
根据基尔霍夫定律和电磁感应定律,得到节气门电机侧的电压平衡方程
(1)
式中R为等效电阻;i为电枢电流;L为电枢电感,因其值很小,故可忽略不计;um为电机反电动势;u为输入电压;km为电机反电动势系数;ωm为电机转子角速度.电机转动产生的扭矩Tm与电枢电流i呈正比Tm=kti=kmi,其中kt为电机扭矩系数,直流电机中扭矩系数kt与反电动势系数km相同.根据刚体定轴转动定律,得到电子节气门运动学微分方程
Jtdω/dt=n(Tm-Jmdωm/dt)-Ts-Tf,
(2)
式中Jt为节气门轴转动惯量;ω为节气门阀片角速度;n为齿轮组传动比;Jm为电机主轴转动惯量;Tf为摩擦力矩;Ts为回位弹簧扭矩,Ts=ksθ+T0,其中ks为回位弹簧的弹性系数,θ为节气门阀片角度,T0为弹簧在初始位置受到的预紧扭矩.本文将摩擦力矩和弹簧初始力矩作为扰动d,d=T0+Tf,以扰动观测的方式进行处理,得到电子节气门的数学模型:
(3)
式中J=n2Jm+Jt为Jt及Jm折算到节气门轴后总的转动惯量.
(4)

2 控制器设计
2.1 干扰观测器
干扰观测器能通过对象的输入/输出及名义模型信息对干扰进行估计,从而有效抑制扰动.根据方程(4),设计基于状态空间的干扰观测器
(5)


考虑系统

(6)
其中f:[0,∞)×Rn×Rm→Rn是关于t的连续分段函数和关于x和u的局部Lipschitz函数.
定义1[12]如果存在一个KL类函数β和一个K类函数γ,使得对于任意初始状态x(t0)和有界输入u(t),解x(t)对于所有的t≥t0都存在,且满足
‖x(t)‖≤β(‖x(t0)‖,t-t0)+γ(supt0≤τ≤t‖u(τ)‖),
(7)
则称系统(6)是输入-状态稳定的.
引理1[12]若连续可微函数V:[0,∞)×Rn→R满足
α1(‖x‖)≤V(t,x)≤α2(‖x‖);
(8)
∂V/∂t+f(t,x,u)∂V/∂x≤-W(x),∀‖x‖≥ρ(‖u‖)>0,
(9)
∀(t,x,u)∈[0,∞)×Rn×Rm,其中α1,α2是K∞类函数,ρ是K类函数,W(x)是Rn上的连续正定函数,则系统(6)是输入-状态稳定的.


(10)
选取Lyapunov函数V=e2/2,对其求导可得
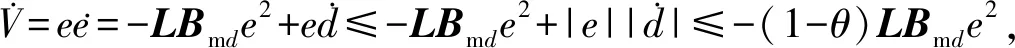
(11)
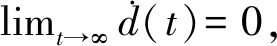
2.2 模型预测控制器

(12)
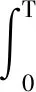
(13)


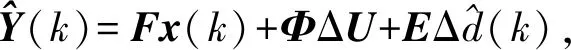
(14)


由于电子节气门受直流电机的饱和限制,控制量一般在-12 V至+12 V,同时阀片的行程为有限区间,其旋转角度在0°至90°间,即弧度为0至π/2;因此,电子节气门控制量的求解是一个约束优化问题,可描述为
(15)

上述约束优化问题可以转化为标准二次规划问题,首先通过有效集法和内点法等方法进行求解,得到控制量序列U=[u(k),u(k+1),…,u(k+Nc-1)],然后将第一个元素u(k)作为控制器当前时刻的输出,再基于更新后的系统状态和输出等重新求解约束优化问题得到下一时刻的控制量,最终实现滚动优化策略.
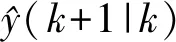
(16)

3 仿真分析
为了验证基于干扰观测器的模型预测控制方案的有效性,笔者在Matlab/Simullink环境下搭建了系统仿真模型,选用的电子节气门具体参数:R=2.01 Ω,km=0.021 7 N·m·A-1,Jt=2×10-6kg·m2,Jm=3×10-6kg·m2,n=40,ks=0.1 N·m·rad-1.将本文控制方案与工业过程中普遍采用的PID(proportion integral differential)控制以及传统的模型预测控制(MPC)进行比较.首先给定一个阶跃信号,观察3种控制器的阶跃响应曲线,在1 s后突加扰动,观察对于扰动的响应.仿真采用离散形式,仿真步长为1 ms,控制器采样周期为1 ms,其中PID控制器中比例项增益kp=10,积分项增益ki=2,微分项增益kd=0,模型预测控制器中预测时域Np=100,控制时域Nc=10,干扰观测器增益L=[0 -1],仿真结果如图2 ~3所示.
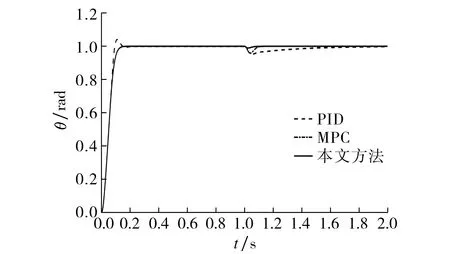
图2 3种控制器的角度响应曲线Fig.2 Angel response of three controllers
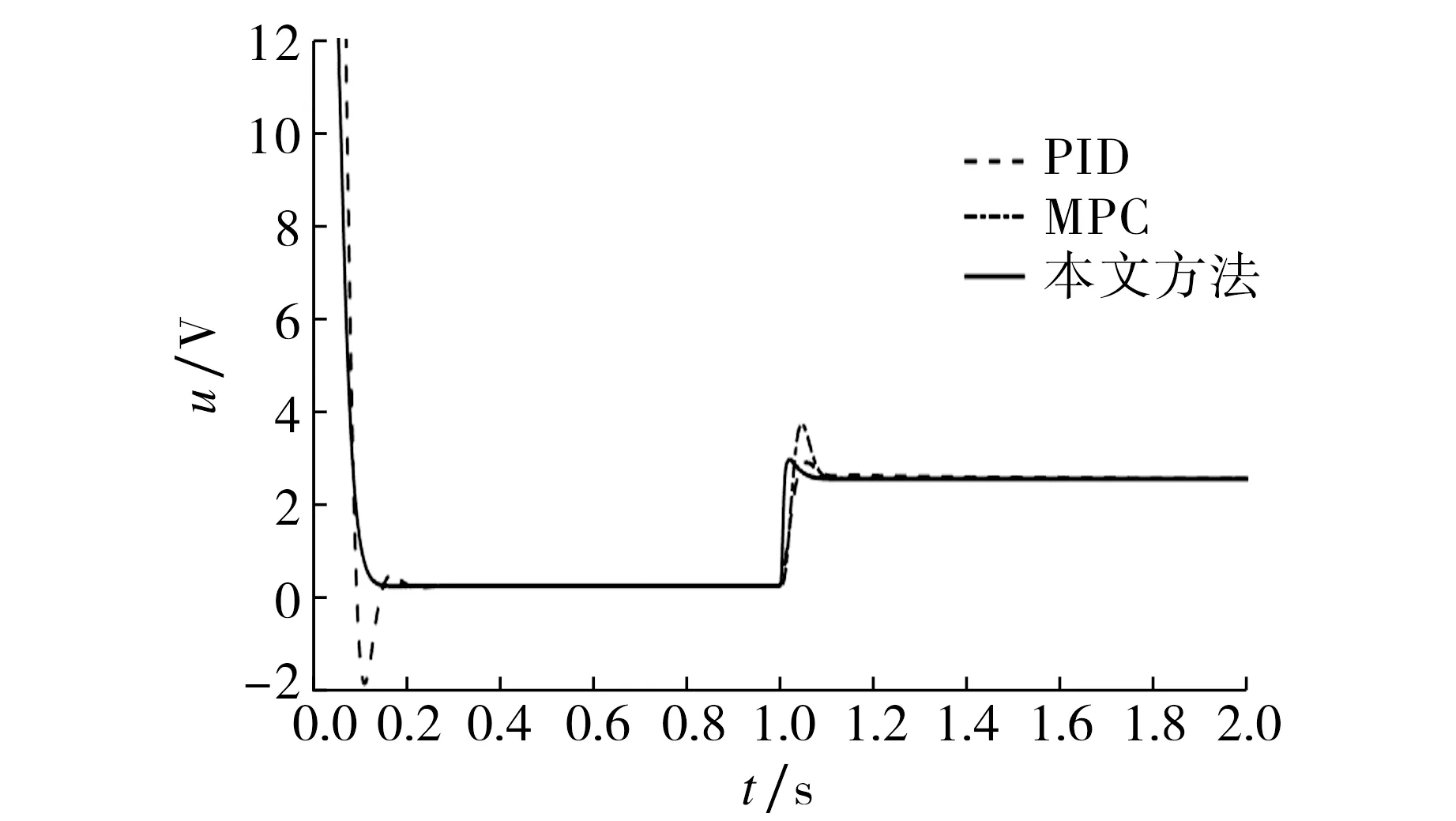
图3 3种控制器的控制量曲线Fig.3 Control volume of three controllers
由图2~3可见: PID方法对阶跃信号的角度响应会出现超调现象从而降低动态性能,而传统的模型预测控制以及基于干扰观测器的模型预测控制对于阶跃信号表现出良好的跟踪能力;在突加扰动时,基于干扰观测器的模型预测控制对于扰动的抑制作用更优,抗干扰能力更强.
