新疆石河子多年气温、降水突变分析

（新疆石河子气象局，石河子市，832000） 韩春光 蒲云锦

气 候 突 变（climate jump，abrupt climatic change，jump transition）是指气候从一种稳定态(或稳定持续的变化趋势)跳跃式地转变到另一种稳定态的现象,它表现为气候在时空上从一个统计特性到另一个统计特性的急剧变化。气候变化是一个非常复杂的问题，存在线性变化的同时也存在着一定的非线性变化,非线性变化指的就是气候的相对稳定性和突变现象等。章名立等[1]指出近百年来,全球气候变暖并日趋加剧已成为公认的事实，但在总的变暖趋势中却有起有伏,有渐变和突变，且气候变化的区域性和季节性差异显著。魏凤英、刘莉红、向辽元、郭志梅等[2-5]从气温的长时间序列中检测到了结论一致的突变点，此外，不同区域的研究者[6-15]也相继发现了本地气候要素存在突变的事实。本文利用新疆石河子多年气温、降水资料，研究其突变事实，为气候预测提供依据。

1 资料与研究方法

1.1 资料整理

选用新疆石河子建站时间早、年代资料完整的石河子市气象站为代表站，从国家气象信息中心取1954～2017年月均气温、月总降水量资料，样本总数n=1296。以3～5月为春季，6～8月为夏季，9～l1月为秋季，l2～2月为冬季。春季气温取3个月的平均值，降水量取三个月的降水总量，据此得到四季、年均气温和降水量分析序列。

1.2 研究方法

气候突变是普遍存在于气候变化中的一个重要现象，是气候预测与模拟要考虑的重要因素。符淙斌等[16-17]在给出气候突变普适定义的同时指出气候突变有均值突变、方差突变、跷跷板突变和转折突变四种基本类型，实际的突变往往是它们的组合。利用突变理论研究均值突变，采用Mann-Kendall 法(简 称M-K)、滑 动T 法（简 称Mtt）和Yamamoto法联合检测气候变化过程中的突变现象,综合M-K 非参数法检测范围宽、人为性少,Mtt 客观、准确，Yamamoto 直观、简便的特点,从而在方法上增强和提高研究结果的可信度和确定性。

1.2.1 Mann-Kendall方法

Mann-Kendall 法是一种非参数统计检验方法[18]，其优点是不需要样本遵从一定的分布，也不受少数异常值的干扰，适用于类型变量和顺序变量，计算也比较简便，而且可以明确突变开始的时间，并指出突变区域。方法是对于平稳随机序列Xi(1≤i≤N),构造统计量：,式中dK=ΣMi，Mi是1至i之间小于Xi的样本数,即Mi={Xj:j＜i且Xi＜Xj}，E[dK]为均值，Var[dK]为方差。在原序列随机平稳假设下,dK的分布渐进正态,U(dK)则为标准正态分布。其概率α可以通过计算或查表获得，给定显著水平α0，若α＞α0，则接受序列无变化的原假设；若α＜α0，则拒绝原假设。把U(dK)沿时间轴绘成曲线UF，而后将序列反向，计算出U(dK),绘成曲线UB,若UF与UB交叉点位于置信区间内,则此点即为突变点。当UF存在明显的变化趋势、超过置信线时, 或是突变增加，或是突变减少。

1.2.2 滑动t检验方法

此法通过考察2组样本平均值的差异是否显著来检验突变。对于总样本量为n的序列x，人为设置某一时刻为基准点，取前后长度分别为n1、n2的两子序列(一般取n1=n2)进行连续的滑动计算，得到t的统计量序列。给定显著性水平a，确定临界值ta，若|t|＜ta，则认为基准点前后的两子序列均值无显著差异，否则认为在基准点时刻出现了突变[18]。

1.2.3 Yamamoto方法

2 流域气温突变分析

三种方法检测出的气温序列突变见图1 和表1。

2.1 年均气温突变

由图1（a、b、c）和表一看出：三种方法均检测出发生在20 世纪90 年代中期的一次明显增温突变。Mtt、Yamamoto法最大t值和信噪比年都在1996年，|t|＝7.14、RSN=1.93，Mtt 通过了a=0.0001 的信度检验,M-K 法中UF、UB 曲线相交于1993 年，落在99%信度线内。

2.2 四季气温突变

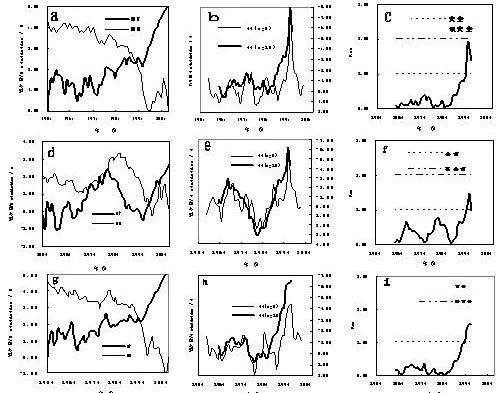
图1 Mann-kendall、滑动t、 Yamamoto法确定的石河子年、季气温序列突变

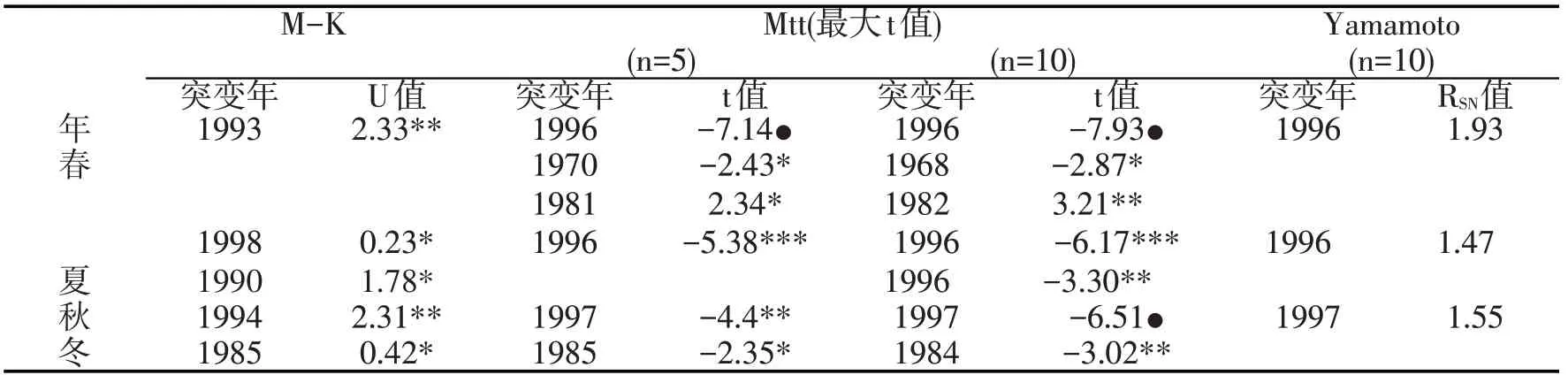
表1 Mann-kendall、滑动t、Yamamoto法检测出的石河子年、季气温突变

1954 年来，四季平均气温均有突变现象发生，且春、秋突变较夏、冬（图略）明显。

春季平均气温有三次突变，20 世纪60 年代末和90年代中期为增温突变，80年代初为降温突变。Mtt 法（图1e）检出第一次增温突变年份在1970(n=5)、1968(n=10)年，通过了a=0.05的信度检验，第二次降温突变年份在1981、1982 年，分别通过了a=0.05和0.01的信度检验，第三次增温突变年份均在1996年，通过了a=0.001的信度检验；Yamamoto法（图1f）第一、二次Rsn 接近1，认为突变不明显，第三次在1996 年，RSN=1.47，发生突变；M-K 法（图1d）UF、UB曲线在95%信度内相交于1998 年。三次突变中以90年代中期1996年出现的暖突变最为显著。

夏季平均气温仅在20 世纪90 年代有一次增温突变，Mtt法（n=10）检出突变年在1996年，检验信度通过a=0.01，M-K法UF、UB曲线在a=0.05信度线内相交于1990年。

秋季平均气温在90 年代中期出现一次增温突变，Mtt法（图1h）、Yamamoto法（图1i）检出突变年都在1997 年，Mtt 法超过了99%的检验信度，M-K 法UF、UB 曲线相交于1994 年，交点统计值U 等于2.31。

冬季平均气温在20世纪80年代中期发生一次增温突变，Mtt法突变年在1984～1985年，M-K法在1985 年，均通过了a=0.05 的信度检验，Yamamoto 法未检出冬季突变。

综合气温年、季突变得出：60 年代末1968～1970 年春季气温发生增温突变；80 年代初1981～1982年春季出现降温突变，80年代中期1984～1985年冬季出现增温突变；90 年代中期1996～1997 年春、夏、秋三季、年气温出现显著暖突变。1996 年春、夏季出现的显著暖突变直接导致同年年气温的显著暖突变。

图2 Mann-kendall、滑动t、Yamamoto法确定的石河子年、季降水序列突变

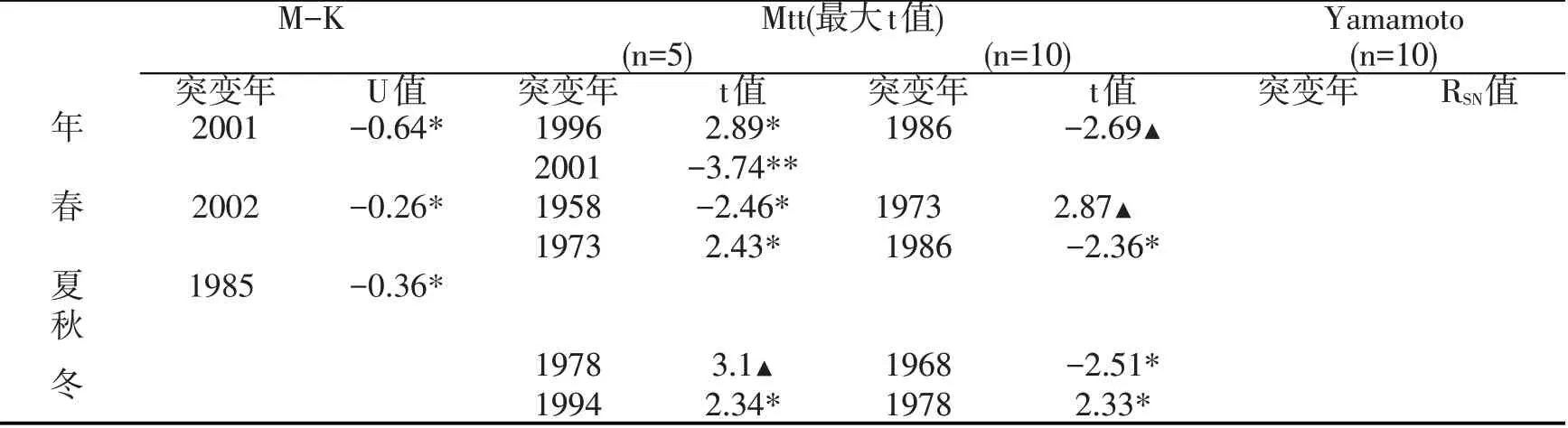
表2 Mann-kendall、滑动t、Yamamoto法检测出的石河子年、季降水突变

3 流域降水突变分析

图2 和表2 为三种方法检测出的降水突变结果。

3.1 年降水突变

检测图中（图2，a、b、c），1986 年的降水增加趋势三种方法曲线上都有反映，但仅在Mtt 法步长n=10时检出增加突变点。Mtt（n=5）、M-K法同时检测出2001 年的降水增加突变，Mtt 法检验信度超过99%，Mtt 法还检测出发生在1996 年的降水减少突变。Yamamoto法年降水突变不明显，下面四季降水突变检测中亦有体现。

3.2 四季降水突变

对比三种方法的检测结果，确定春季降水（图2d）在50年代末的1958年有一次增加突变，70年代初期的1973 年有一次减少突变，80 年代中期1986年有一次降水增加突变，M-K 法(图略)还检测出2002年的一次降水增加突变；夏季降水（图2e）仅在80 年代中期的1985 年有增加突变；秋季未出现突变；冬季降水（图2f）在60 年代末期的1968 年有一次降水增加突变，70年代末期的1978年、90年代中期的1994年各有一次减少突变。

综合降水年、季突变得出：50 年代末期1958 年石河子春季降水发生突变增加；60年代末期1968年冬季降水突变增加；70 年代初期1973 年春季、后期1978年冬季发生降水突变减少；80年代中期1985～1986 年春季、夏季、年降水突变增加；90 年代中期1996 年前冬季、年降水出现突变减少；21 世纪初的2001～2002 年，年、春季降水突变增加。1986 年春季降水的突变增加直接导致同年降水的突变增加。

4 结论

（1）应用三种方法检测突变，得出结果不尽相同，Mtt步长不同检测点亦不同，气温检测中对出现的较显著突变点Mtt 和yamamoto 法有一致结果，降水检测中yamamoto法不敏感。由此看出，不同方法灵敏性不同，应将多种方法结合使用并给定严格的检验信度，以增加突变检测点的可信度和确定性。

（2）多年来，石河子年、四季气温均发生突变，春、秋突变较夏、冬明显。年气温在1996 年发生显著暖突变；春季气温发生三次突变：1968、1970年和1996年为暖突变，1981、1982年为冷突变；夏、秋、冬季均发生暖突变，夏季突变年在1996 年、秋季在1997年、冬季在1984～1985年。

（3）除秋季外，年和春、夏、冬三季降水都有突变。年降水在1986、2001 年发生增加突变，在1996年发生减少突变；春季降水在1958 年、1986 年和2002 年发生增加突变，1973 年发生减少突变；夏季降水仅在1985年发生增加突变；冬季降水有一次增加和两次减少突变，1968 年为增加突变，1978 年、1994年为减少突变。

（4）气温虽较降水突变明显，但互有影响。1996年春、夏季出现的显著暖突变直接导致同年年气温的显著暖突变，1986年春季降水的突变增加直接导致同年降水的突变增加，1996年气温的显著暖突变引起同年年降水的显著减少突变。