基于2D Chebyshev-Sine映射的图像加密算法

2019-04-15钟艳如刘华役孙希延蓝如师罗笑南

浙江大学学报（理学版） 2019年2期

钟艳如，刘华役，孙希延，蓝如师*，罗笑南

（1.桂林电子科技大学计算机与信息安全学院，广西桂林541004；2.桂林电子科技大学信息与通信学院，广西桂林 541004）

0 引言

21世纪是信息科技时代，伴随着计算机技术的迅速发展，通信信息技术与多媒体技术互相融合、渗透，成为信息技术的实质。互联网时代，许多通信设施具有开放和共享的特点，安全问题正接受有史以来最严峻的考验。传统的信息加密方式只适用于纯文本类型的数据加密，而其他类型的信息，如图像数据信息［1⁃3］，并不可用。由于图像数据信息具有存储量大、冗余性高、相关性极高的特性，研究者从各个方面对图像数据信息进行了研究。随着混沌理论的出现，研究者将其应用于图像加密，发现其与密码学有密不可分的联系［4-6］，于是，就形成了基于混沌的图像加密算法［7］，有混沌映射［8-9］、波扰动［10］、小波变换［11-12］和魔方变换［13］等。

混沌图像加密算法可分为一维混沌系统、高维混沌系统。一维混沌系统包括Logistic映射、Sine映射、Tent映射、面包师（baker）映射以及各种一维映射的混合等，因其具有简单、快速的特点，一直被用于各种加密算法。蒋爱平等［14］提出了一种基于超混和改进AES的图像加密算法，利用超混沌Qi系统的混沌序列对灰度图像进行了加密和二值化，该算法比传统的AES算法具有更大的密钥空间，增强了图像信息的保密性。赵芮等［15］提出了基于二维Logistic与Chebyshev映射的AES混沌加密算法，克服了传统AES算法中由密钥唯一导致的安全性低的缺点，实验结果显示，该算法较传统AES算法具有更高的安全性。 ZHU等［16］提出了用Arnold猫图的对称图像加密方案。ZHOU等［17］提出了一种新的图像加密1D混沌系统，一维混沌映射，其混沌轨道很简单，易被预测，信息一旦被提取［18-20］，很可能通过某些技术计算出其初始状态［21-24］。因此，一维混沌系统的图像加密方案很容易被攻击［25-28］，须有更高维的混沌映射。 2DSLMM［7］，2D-LASM［29］，2D-SIMM［30］的混沌轨道较一维的复杂，也不容易被预测，但其硬件实现较困难。为此，本文提出了一种具有良好混沌性能和低消耗成本的混沌映射。

为了进一步提高基于线性层组合的图像加密算法的安全性能，本文通过使用AES算法产生的序列来控制二维Chebyshev映射与Sine映射的密钥，利用行移位和列混合，改变图像像素空间位置和像素频域中的值，最后根据中国剩余定理的增强扩散操作对图像进行二次加密。同时，给出了仿真的实验结果与安全性分析。

下文组织如下：第1章，介绍二维Chebyshev映射与Sine映射，并对轨迹图进行分析；第2章，新的图像加密算法——线性层组合，介绍线性层组合，包括行移位和列混合；第3章，对此算法做仿真实验和时间复杂度分析；第4章，分析线性层组合算法的安全性；第5章为结论。

1 2D Chebyshev-Sine映射

1.1 定义

以下是本文用到的2个一维映射，分别为Chebyshev map［15］和 Sine map，其定义分别为：

其中，u和n为参数，u在［0，1］范围内，n在［0，4］范围内。

此2映射均为非线性变换，用以生成简单结构的下一个迭代值。因此，通过混沌信号易预测其轨道。为解决这一问题，本文提出了一种新的二维混沌映射——Chebyshev-Sine map方法，定义为

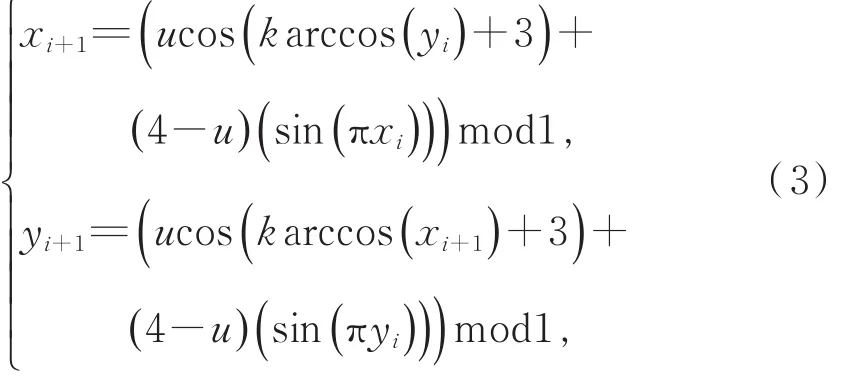
其中，u和k都为参数，u的取值范围为［0，4］，k的取值范围为［0，1］，当k=0.162 5，u=1.5时，具有混沌行为。

1.2 2D Chebyshev-Sine映射性能的评估

本文提出的2D Chebyshev-Sine map具有良好的混沌行为。通过生成的轨迹来判断其混沌性能。

图 1显示了 2D Chebyshev-Sine map、2DSLMM［7］的轨迹图，并设置他们的初始值均为的（x0，y0）=（0.3，0.4）。显见，2D Chebyshev-Sine map在相平面上的轨迹较2D-SLMM分布更宽广，因此，2D Chebyshev-Sine map具有更好的遍历性，其输出也是随机的。

2 线性层组合图像加密算法

图2为2D Chebyshev-Sine map的图像加密算法流程图，包括原文图像、安全密钥、2D Chebyshev-Sine map、密文图像以及核心的行移位、列混合、中国剩余定理扩散的原则。图3为解密过程流程图，加密过程为C=Enc（P，K），解密过程为P=Dec（C，K）。

2.1 安全密钥的结构和2D Chebyshev-Sine映射序列发生器

图1 轨迹图Fig.1 The trajectories

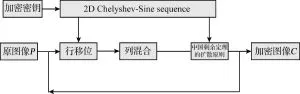
图2 加密流程图Fig.2 Encryption flow chart

图3 解密流程图Fig.3 Decryption flow chart

将加密的安全密钥K值定义为256位字符串序列，分别由x0、y0、q、A、B1、B2、B3、B4组成，如图 4 所示。其中（x0，y0）和q是二维 Chebyshev-Sine映射的初始值和控制参数。A和B的目的是改变初始值和控制参数，以增大安全密钥。

图4 安全密钥的结构Fig.4 Structure of security key

具体来说，通过使用 IEEE 754［31］格式的 52 位字符串（b1，b2，…，b52）来生成十进制的数值x0，y0，q，A，公式为

B1，B2，B3，B4由 12位字符串｛b0，b2，…，b11｝组成，将这12位字符串转换为整数并获得所需的系数。对于每一轮的初始值可定义为

2.2 行移位变换

如果明文图像P的大小为M×N，那么图像P中像素点的总量为M×N，由式（3）生成X和Y序列。

现在使用行移位变换对二维Chebyshev-Sine映射生成的X序列进行转换，其中图像（M—1）行的像素点被循环偏移到同行不同列的像素位置上，而图像的元素值未发生任何变化。假设矩阵为state，行移位变换公式为

state´[i][j]=state[i][(j+i)%n],n∈ N。（6）

图5 行移位的变化Fig.5 The change of row shift

2.3 列混合变换

在1.1节中，通过式（3）生成X和Y序列，X已对行移位做了变换。现用Y序列通过矩阵相乘对图像进行列混合变换，即经行移位后的状态矩阵与固定的矩阵相乘，得到混淆后的状态矩阵。

列混合变换操作：将每一列视为一个t项多项式。现对t=4用四项多项式进行列操作。这些列为 GF（28），乘以模x4+1，其固定多项式a（x）定义为

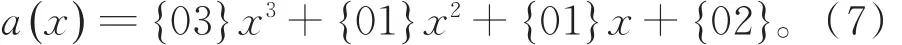
根据 Polynomials with Coefficients in GF（28），可将其写成矩阵形式。令

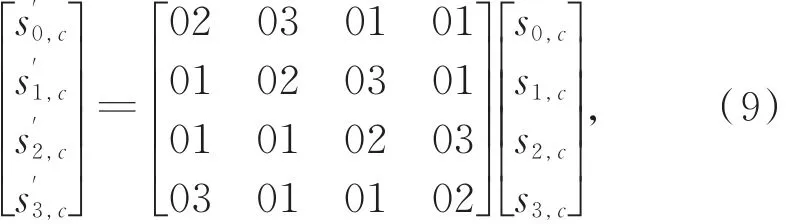
对

根据上述矩阵乘法，可将图像中列的像素数替换为：

图6给出了列混合变换。

图6 加密算法列混合的变化Fig.6 The changes in column mix of encryption algorithm

2.4 中国剩余定理的扩散原则

通过行移位和列混合操作得到的密文图像很容易被破译。于是提出了中国剩余定理［32-34］的扩散原则。

2.4.1 中国剩余定理

定理1 设g1，g2，…，gk为k个两两互素的整数，Gi-1为Gi模gi的乘法逆元，满足GiGi-1≡1（modgi），i=1，2，…，k。对于任意给定的k个整数：b1，b2，…，bk（k≥2），一次同余方程组：

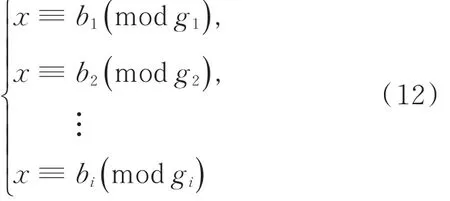
有唯一解

该定理通过将k个整数转化为一个较大的整数实现加密。

2.4.2 中国剩余定理的扩散原则

将行移位和列混合操作之后的密文图像进行转化。将密文图像转化为一维序列P（p1，p2，…，p（M×N））。下面用中国剩余定理扩散原则，随机选取s个两两互素的整数m1，m2，…，ms，其中mi＞28。

将转化后的一维序列P（p1，p2，…，p（M×N））分成s组：

将pi代入式（12）和（13），计算得到序列Qi=｛Q1，Q2，…，Q（M×N）/s｝。再对得到的Qi序列进行取模28，得到加密序列D=｛D1，D2，…，D（M×N）｝，最后将加密序列D转化成二维图像矩阵，得到加密图像。

经上述行移位和列混合后，再对密文图像进行中国剩余定理扩散。

3 仿真实验结果和时间复杂度分析

验证一个图像加密算法是否具有良好的遍历性和混沌行为，主要看其能不能将不同类型的明文图像转化成随机的密文图像。本文对线性组合算法进行了仿真实验，并与其他图像加密算法的运行时间进行了比较。

3.1 直方图分析

直方图是验证图像加密算法是否良好的最直观方法之一。密文直方图的平坦程度直接影响算法的安全性，密文直方图越平坦，破译者越难得到明文信息。因为一个好的图像加密算法可以将明文图像加密成类似随机密文图像，而直方图是均匀分布的。图7为线性层组合算法的图像仿真实验。可将所有图像转换成类似噪声的密文图像，反映图像像素点所在灰度的分布情况［35］，分布越均匀，越难辨别，可视化能力越差。通过图7知，所有明文图像的直方图具有某种特定的模式。若将明文图像加密成密文图像，又不呈现任何明文图像信息，则说明此算法具有良好的加密性能。

3.2 时间复杂度分析

线性层组合算法具有较高的加密速度。在Matlab下通过测试使用数据集的图像，得到CCM的加密/解密时间是0.038 001 s。表1为图像的平均加密时间，发现线性层组合算法比其他二维加密算法快些，但明显较一维算法慢。原因在于一维的结构较简单，本文方法是基于复杂的二维混沌结构的。因此，线性组合算法以较短的运行时间、良好的加密性能胜出。

4 安全性分析与测试

为了验证线性层组合算法的安全性能，本节采用以下方法进行分析，测试图像基本来自USCSIPI‘Miscellaneous’图像数据库。

图7 线性层组合的仿真实验结果Fig.7 Simulation results of linear layer combination

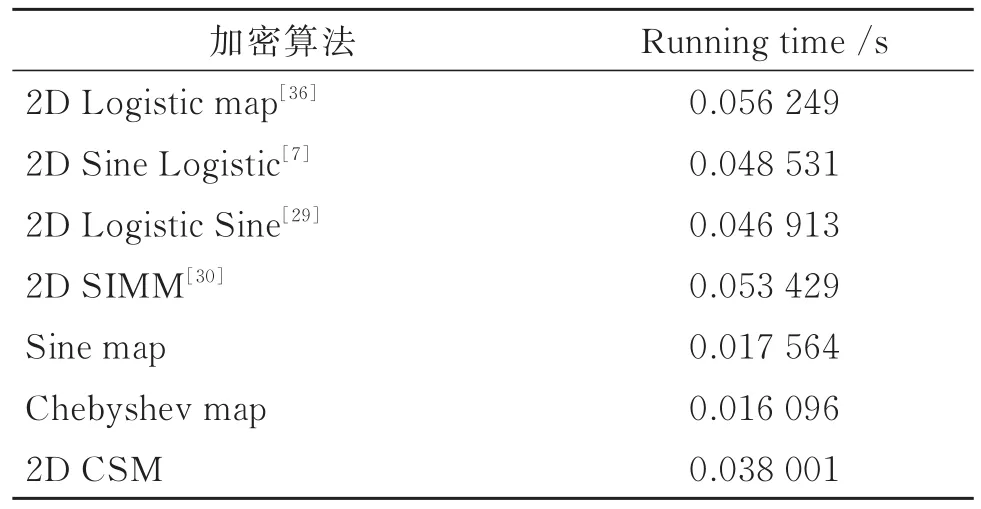
表1 不同图像加密算法的运行时间对比Table 1 Comparison experiments on running time of different image encryption algorithms

4.1 安全密钥分析

为有效抵抗强有力的攻击，图像加密算法应该对安全密钥十分敏感，且确保密钥空间足够大。即安全密钥的敏感性可从以下两方面校正：

（1）如果加密端的安全密钥与原密钥有微小差异，那么得到的密文图像应该完全不同。

（2）如果解密端密钥与加密端密钥有微小差别，那么得到的明文图像无法被正确解密。

图8和图9展示了本文算法在加密与解密方面的敏感性分析结果。其中，K1为原安全密钥，K2与K1间有1个比特字节之差，K3与K1间有1个比特字节之差。当用K1、K2分别对明文图像进行加密时，得到的密文图像是完全不同的，这2幅加密后的图像的差异为|C1―C2|。该算法证明了加密过程中安全密钥的敏感性，现对解密过程进行验证。用K1对加密后的图像进行解密，得到的图像可恢复为原始图像。用K2、K3分别进行解密，得到完全不同的图像，且无法辨别。解密后的图像也存在差异，差异为|D2－D3|。证明了解密过程中安全密钥的敏感性。

图8 加密过程中安全密钥的分析Fig.8 Analysis of the security key in the encryption process

图9 加密过程中安全密钥的分析Fig.9 Analysis of security keys in the encryption process

4.2 信息熵测试

图像的直方图非常明了，可用于检验密文图像像素分布是否均匀。如何判断图像直方图分布的好坏是一个比较难的问题。本文引入香农理论，用信息熵来判断图像灰度值的分布是固定还是随机的。一个图像粗糙程度越大，信息量就越大，得到的信息熵也就越大。反之，图像越平滑，得到的信息熵就越小。对于一个灰度值为256的随机图像，理想的信息熵为8，安全性能越强，图像被攻击的可能性越小，熵的计算公式为

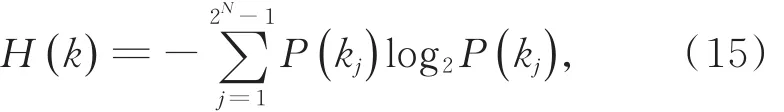
P表示符号kj的概率。

为保证实验的客观、公平，直接使用吴算法、周算法、吴氏算法以及Hua’s算法。表2列出了各算法的平均信息熵。由表2可知，本文算法平均信息熵更接近理想值8，密文内容不容易泄露，安全性较高。

表2 各图像加密算法的信息熵测试值Table 2 Information entropy test value on different image encryption algorithms

4.3 差分攻击测试

差分攻击又称为选择明文攻击，是在特定区域，将原始图像加密后来攻击密码的算法。验证一个加密算法是否具有扩散性，主要看是否能够抵抗差分攻击。像素变化率（NPCR）和统一变化强度（UACI）是图像加密算法中最常用的2种度量方法［39］。 PCR（C1，C2）和 UACI（C1，C2）在 2 幅密文图像C1和C2之间的分数定义为：

其中，K（i，j）表示函数，C1和C2表示在图像网格（i，j）上的2个像素，T和L表示图像中的像素数和允许的最大像素强度。由式（16）和（17）知，NPCR和UACI的预期分数取决于最大像素强度L。当选取的测试图像灰度为8位时，得到的NPCR和UACI的预期分数分别为99.609 6%和33.46%。

从USC-SIPI‘Miscellaneous’图像数据集中选取27个测试图像进行了实验测试。原图像像素改变1个比特值，生成一个新的明文图像，然后对2个明文图像用相同的安全密钥进行加密。为保证公平并兼顾方便，直接使用 WU［36］、ZHOU 等［37］、WU 等［38］、HUA等［7］的NPCR和UACI测试分数。表3和表4分别为NPCR和UACI的实验结果。由表3和表4知，本文的加密算法与预测分数相似。因此，线性层组合具有很好的抗差分攻击能力。

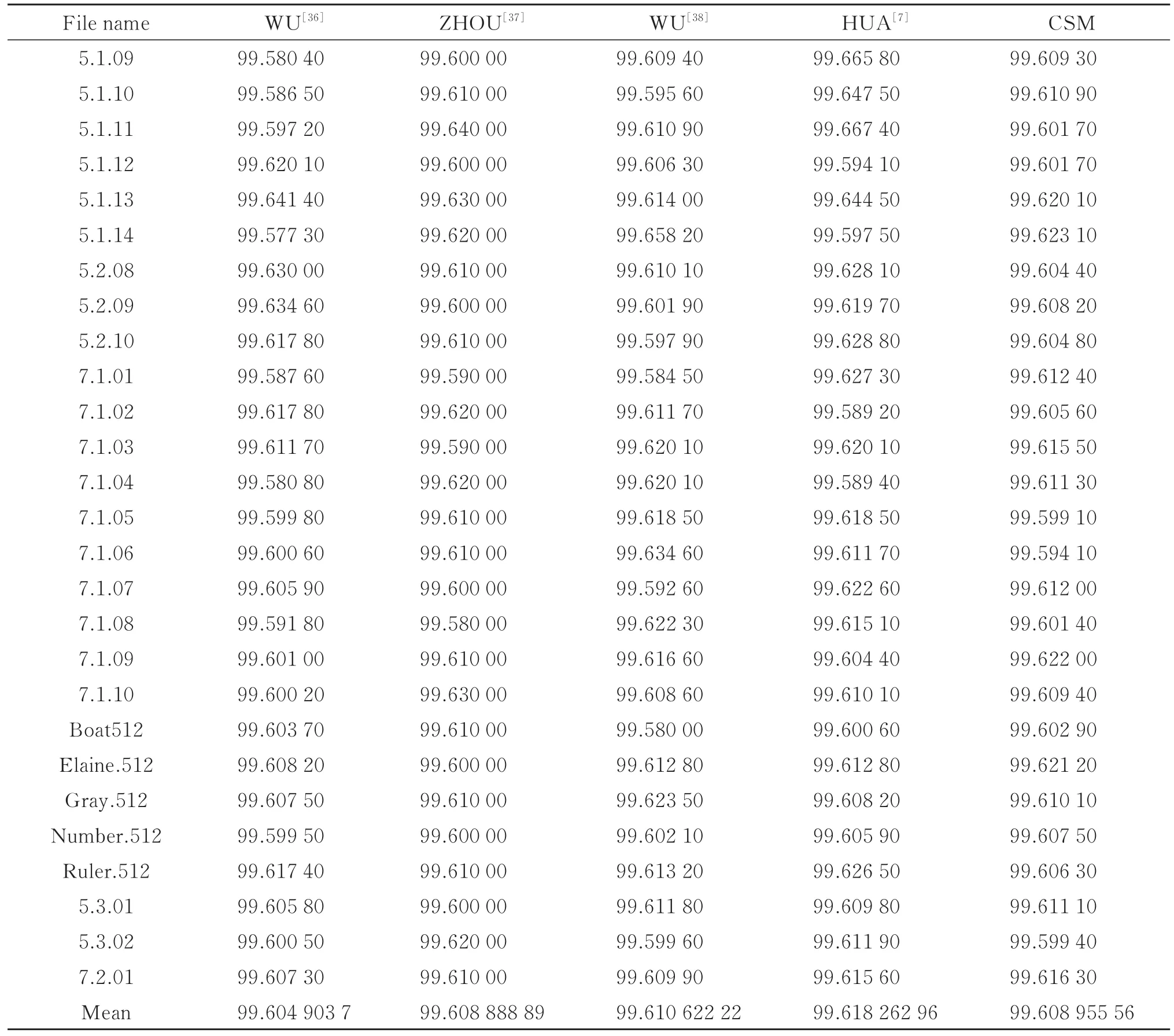
表3 各图像加密算法的NPCR测试值Table 3 The NPCR test value on different image encryption algorithms

4.4 相邻像素相关性测试

对于灰度值为256的图像来说，像素与邻近的像素之间具有很强的相关性，攻击者常利用此原理寻找明文图像和密文图像之间的关系。所以往往通过相邻像素之间的相关性来验证图像加密方案的优劣［40］。由式（18）计算相邻像素的相关系数：

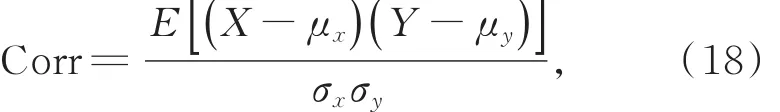
其中，x，y分别为图像的2个数据序列，μ，σ分别为平均值和标准差。通过计算得到它们的相关值约为1，说明2个序列X，Y具有很强的相关性，反之接近于0。

从明文图像和密文图像中随机选择2 000对相邻的像素，并分别研究水平方向、垂直方向和对角线方向的像素分布。明文图像“elaine”图在水平方向、垂直方向及对角线方向相邻像素的相关分布和密文图像相邻像素的相关分布如表5所示。其中，明文图像的结果接近于1，密文图像的结果接近于0。图10为图像加密前后的像素序列对的分布情况，可看出明文图像相邻像素的值彼此接近，而密文图像相邻像素的值发生了变化。从而验证了线性层组合算法可大大降低相邻像素间的相关性。

4.5 相似度测试

在图像加密中，常常比较2个图像是否相同。如果加密后的图像与原图像相似地方较多，说明此加密图像的安全性能较差。下面给出2个图像相似度参数XSD的计算式［41］，以判断2个图像是否相似：

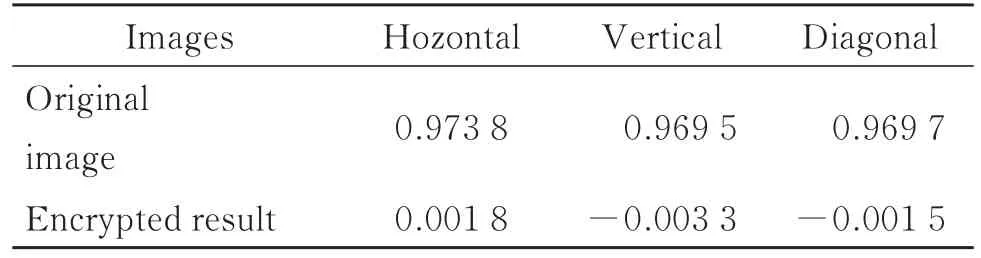
表5 Elaine原图像像素与其加密图像像素的相关性Table 5 The correlation between the original image of Elaine and the pixels of its encrypted image

其中，G=（gij）m×n，C=（cij）m×n为 2个灰度图像。α，β为 2个十进制数，并且α∈［0，m-1］，β∈［0，n-1］。

由式（19）知，Cij与Gij的值相差越大，2个图像的相似度就越小。对加密图像而言，与原图像的相似度越小，安全性能就越高。因此，用图像elaine进行测试，分别用2D Logistic［36］、Hénon［42］、2D Sine logistic［7］、2D Logistic Sine［29］、2D SIMM［30］、CSM 对图像进行加密。表6为图像各加密算法的相似度，加密前后图像相似度越低，加密性能越好。可得CSM是性能良好、安全强度高的图像加密方案。

图10 图像相邻像素序列对的分布Fig.10 The distribution of adjacent pixel sequence pairs

表6 Elaine图像的相似度分析Table 6 Similarity analysis of Elaine images

4.6 抗噪声和数据丢失测试

图11 抗噪声和抗数据丢失结果Fig.11 The analysis results of anti-noise and data loss

图像在传输过程中，部分数据不可避免地会受到高斯噪声和盐噪声的影响，且存在丢失的可能。图像加密算法对数据丢失造成的影响应具有免疫功能，即图像在传输过程中具有抗噪声和抗数据丢失的能力。本文的线性层组合算法具有抗噪声和抗数据丢失的能力。图11给出了线性层组合抗噪声和抗数据丢失的鲁棒性分析结果。从图11可以看出，即使密文图像受不同类型噪声的干扰或有不同程度数据缺失，线性层组合算法在解密过程中仍能将图像复原。尽管复原后的图像还存在一些噪声，但大部分已可识别。实验结果表明，本文算法在抗数据丢失和抗噪声攻击上性能良好。