干支流洪水作用下的水利工程洪水漫顶风险率计算研究

甘富万，张华国，覃丽娜，高 扬，黄宇明，肖 良

(1.广西大学土木建筑工程学院，广西 南宁 530004；2.广西大学工程防灾与结构安全教育部重点实验室，广西 南宁 530004)

0 引 言

水库的防洪标准[1]是与大坝的防洪安全密切相关的。大坝防洪安全最值得关注的是洪水漫顶[2]，洪水漫顶是影响水利工程安全的一个重要因素。因此，洪水漫顶风险率的计算分析对于大坝的防洪安全至关重要。大坝防洪风险分析的方法主要有直接积分方法、一次二阶矩方法和蒙特卡罗模拟方法。直接积分法[3]可求得精确解，但由于涉及多重积分的问题，只适用于低维且调洪函数为简单表达式的情况。一次二阶矩方法要求计算函数对变量的偏导数，只能给出近似结果，如莫崇勋、董增川等[4]采用一次二阶矩法计算澄碧河水库漫坝风险。蒙特卡罗模拟方法是通过对实测资料统计分析，确定合适的随机模型，然后应用随机模型，生成足够多的、各种可能组合形式的洪水过程，供水库调洪计算所用，如梅亚东和谈广鸣[5]采用蒙特卡罗模拟法计算大坝防洪安全综合风险率；吕弯弯等[6]运用蒙特卡罗法计算土石坝洪水漫顶风险率的模型，分析洪水、风浪、水库运行调度方式和水库特性对洪水漫顶风险率的影响。

传统的大坝洪水漫顶风险率计算方法通常只对洪峰流量进行单变量频率分析经调洪演算计算漫坝风险率。后来，越来越多学者认为洪水是一个多变量的随机事件，研究了同时考虑洪峰洪量的两变量洪水频率分析的大坝洪水漫顶风险率[7]，表明两变量洪水频率分析更合理，以上都是仅基于单一洪水作用下的洪水漫坝风险率研究。然而随着我国经济的快速发展，越来越多沿江城市在穿越河流的支流入汇处修建了大量的水利工程，这些工程同时起着抵御外江洪水倒灌和保证城市排涝及生态需水等多重作用。对于这些干支流洪水作用下的水利工程而言，漫顶风险率的计算需要考虑干支流洪水的共同作用。目前国内外研究较多的是入库洪水、泄流能力、水库调度规则等对漫顶风险率计算的影响，还未见对于同时考虑干支流洪水对漫顶风险影响的研究。为此，本文通过引入Copula函数，开展基于Copula函数的干支流洪水作用下的水利工程洪水漫顶风险率的研究，分析不同Copula函数以及不同干支流洪水相关性对漫顶风险率计算的影响。

1 干支流洪水作用下的水利工程洪水漫顶风险率计算模型

1.1 大坝洪水漫顶风险分析模型

洪水漫顶风险率是坝前最高水位Z超过坝顶高程Zd发生的概率，可表示为

Pf=P(Z>Zd)

(1)

一般而言，坝顶高程Zd随机变动幅度变动不大，可将它视为确定值。坝前最高水位Z则存在着诸多不确定的因素，如入库洪水过程的不确定性，泄流能力的不确定性等，因此坝前最高水位Z属于随机变量，漫顶率的计算可转化为坝前最高水位Z的分布研究，一旦累积分布F(Z)确定，漫顶率就可以通过Pf=P(Z>Zd)=1-F(Z)计算求得。

由于干支流洪水作用下水利工程的设计洪水位不仅会受支流洪水的影响还会受到干流洪水顶托影响，利用坝址洪水进行调洪演算反推坝前水位Z时需考虑干支流洪水流量间的相关性。因此，本文将采用Copula-Monte Carlo模拟法求解干支流洪水作用下水利工程的洪水漫顶风险率。

1.2 基于Copula的干支流洪水联合分布

Copula函数可用来描述多变量水文要素间的相关性，可构造出边缘分布服从任意分布的联合分布。假设X干和Y支分别表示干流和支流的洪水流量，则二维Copula函数为

F(x干，y支)=Cθ(F(x干)，F(y支))=Cθ(u，v)

(2)

式中，F(x干，y支)为干流和支流洪水流量的联合分布，u=F(x干)，v=F(y支)分别为边缘分布函数。

本文选取5种常用的阿基米德Copula函数，即GH、Frank 、AMH、Clayton和CClayton Copula函数来描述干支流洪水间相关结构，其中，GH和CClayton Copula均具有上尾相关性，相关系数分别为2-2-1/θ和2-1/θ，Clayton Copula具有下尾相关性，Frank和AMH Copula函数则是尾部渐近独立的。采用K-S检验法对五种Copula函数进行假设检验，利用图形分析法、AIC信息准则法、均方根误差法进行优选。

1.3 Copula-Monte Carlo方法计算漫顶率

漫顶风险率的核心内容是获取坝上水位的分布。本文采用的Copula-Monte Carlo方法的模拟思路为：

(1)根据建立的干支流洪水联合分布函数，可以得到当x干为指定值时Y支的条件分布，数学表达式为

SX干(y支|X干=x干)=∂F(x干，y支)/∂x干

(3)

(2)产生服从[0，1]均匀分布的两个独立的随机数n1和n2。

(3)令n1为x干发生的不超过概率F(x干)，根据其反函数得到x干，即

x干=F-1(u)

(4)

(4)令n2为x干发生时y支的条件概率值，根据条件概率的反函数可得到y支，即

(5)

(5)由步骤(3)和(4)即可抽取一对干支流洪水组合流量(x干，y支)，将该组合洪水组合代入调洪模型进行计算，可得到该组合对应的坝上水位。

(6)重复上述步骤n次，可以模拟出n个坝上水位Z值。当模拟的样本容量足够大，采用数学期望公式计算经验频率，获得坝上水位的累积分布函数F(Z)，再利用公式Pf=P(Z>Zd)=1-F(Z)可得洪水漫顶率Pf。

2 实例应用

2.1 工程概况

桂平航运枢纽位于广西桂平市郁江河段，是一个集航运、发电、灌溉、交通于一体的综合利用性航运枢纽工程，处于郁江与浔江干流(包括黔江、浔江)汇合口附近的郁江段，主要由船闸、溢洪坝及水闸组成。桂平航运枢纽同时受到郁江支流和浔江干流洪水的作用，正常挡水位29.6 m，死水位28.6 m，坝顶高程为47.8 m，工程等级为2级。

2.2 干支流洪水联合分布构建

浔江干流选择大湟江口站1951年～2010年最大洪峰流量系列，郁江以大湟江口站发生最大洪峰流量的时间为控制，统计贵港站相应场次洪水的相应洪峰流量并进行频率计算及P-III型曲线适线得到边缘分布，参数估计和检验结果见表1。

表1 边缘分布参数估计及检验结果

计算两变量间的Kendall相关系数τ为0.158 5，采用Kendall相关系数法计算5种备选Copula函数的参数θ，如表2所示。表2还给出了K-S检验值，均方根误差值，AIC值，经验值与理论值的拟合效果如图1所示。从表2可看出，5种备选Copula函数均通过了K-S检验，但Clayton Copula函数的均方根误差和AIC值最小，被选为最优的Copula函数。

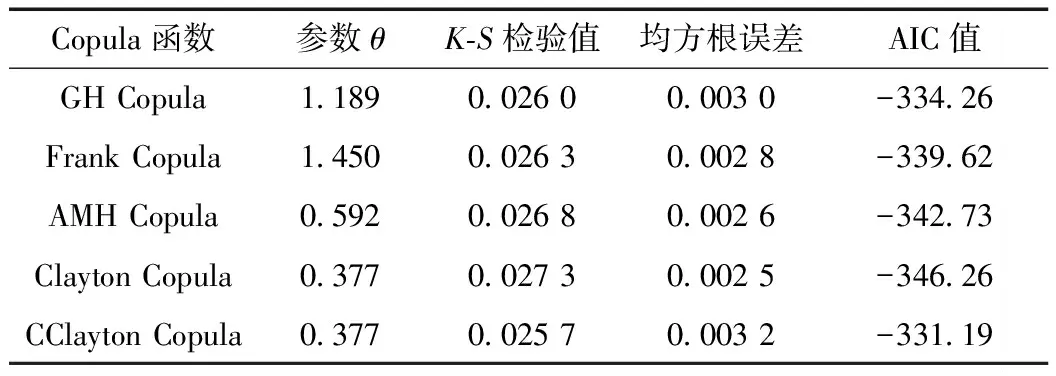
表2 五种候选Copula函数参数估计与拟合检验结果

图1 经验频率与理论频率拟合

2.3 漫顶计算结果

根据1.3节中Copula-Monte Carlo方法的模拟思路，随机生成50万组干流流量、支流流量组合，最优Copula随机模拟的浔江、郁江洪水流量点据与实测点据的对比如图2所示。查询坝址水位与浔江流量、郁江流量的关系表，通过插值可得到50万组洪水组合所对应的坝址水位。根据桂平航运枢纽的调度规则[9]进行调蓄计算可得到对应的50万个坝上水位。最优Copula函数的坝上水位的累积分布曲线见图3。为了更好地展示结果，只给出了累积概率值大于0.95，即重现期20年一遇的上尾部分。由图3可看出，桂平航运枢纽坝顶高程47.8 m所对应的累积分布概率F(Z)为0.999 862，相应的漫顶率Pf=1-F(Z)=1.38×10-4，表明桂平航运枢纽有着较高的防洪安全度。

图2 最优Copula蒙特卡罗模拟点与实测点比较

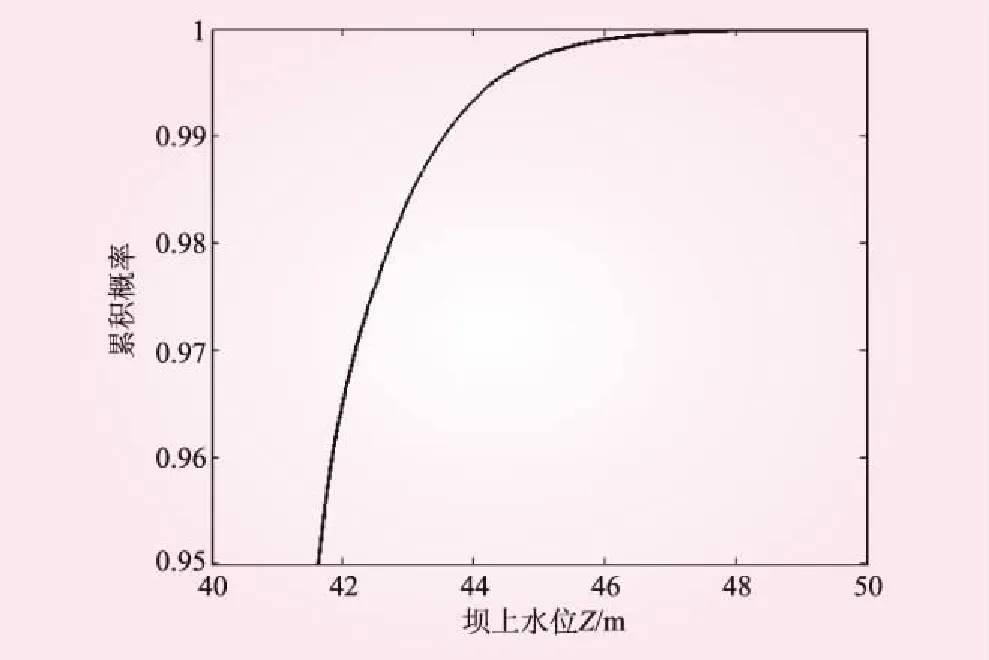
图3 最优Copula函数的坝上水位累积分布曲线

2.4 不同Copula函数对洪水漫顶影响

一般来说，不同的Copula函数描述干支流洪水两变量间的相关关系是不一样的，因此有必要对不同Copula函数进行比较，分析不同Copula函数构造联合概率分布函数对洪水漫顶的影响，如图4所示。从图4中可以看出，不同Copula函数对洪水漫顶的影响并不明显。出现这种现象的主要原因有两方面：①由于本研究区域的干支流洪水间相关性为0.158 5相对较小，由Copula函数理论可知，当变量相对独立时，不同Copula函数收敛于独立Copula函数，此时不同Copula函数之间没有差异。当相关性增加时，不同Copula函数差别随相关系数的增加先增大后减小。因此，不同Copula函数间差异与相关性有着一定联系。也就是说，当模拟的干支流洪水间相关性较小时，不同Copula函数对洪水漫顶的影响不会太大。②水位等值线接近与X轴垂直，略微向左倾斜(见图5)，因此相比支流流量Q贵港而言，干流流量Q大湟对坝上水位的影响更大。然而，从表2中可以看出，大湟江年最大洪峰流量的变异系数Cv小于贵港相应洪峰流量的Cv，从而导致不同Copula函数对洪水漫顶的影响较小。

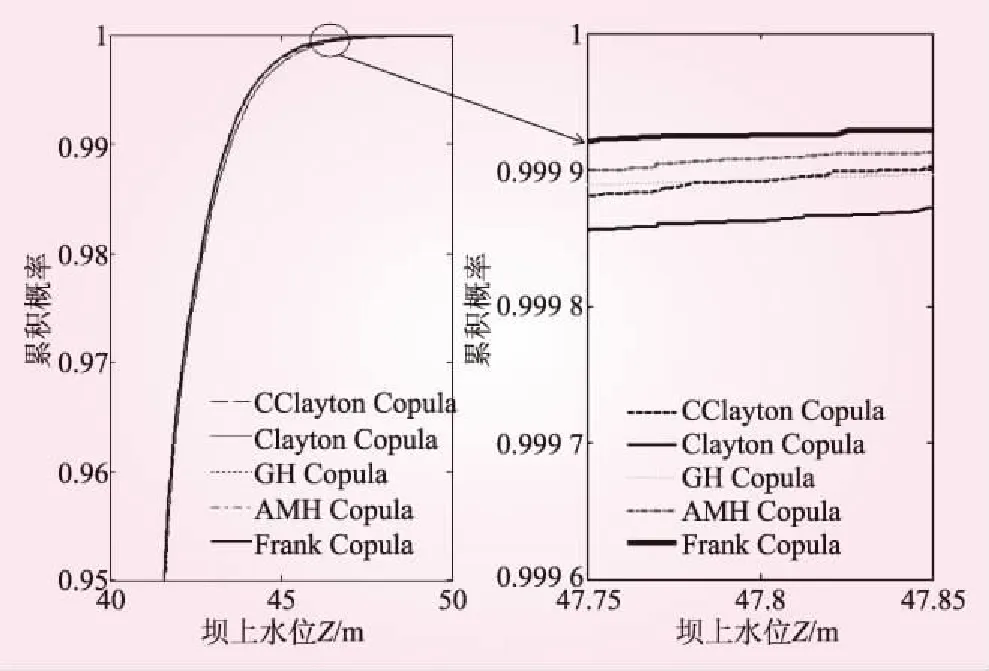
图4 五种不同Copula函数坝上水位累积分布曲线

图5 不同设计重现期对应的坝上水位

由图4中还可看出，GH、CClayton、AMH、Frank Copula均位于Clayton Copula的上方，会低估洪水风险。具有上尾相关性GH、CClaytonCopula函数计算的洪水漫顶率略高于上下尾部均为0的AMH、Frank Copula，可见尾部相关性对洪水漫顶率的计算也产生了一定影响。5种Copula函数计算的洪水漫顶率结果见图6。由于大坝失事将会带来十分严重的后果，工程上往往采用更保守的设计，因此采用最优的Clayton Copula函数计算的洪水漫顶率更符合工程设计要求。

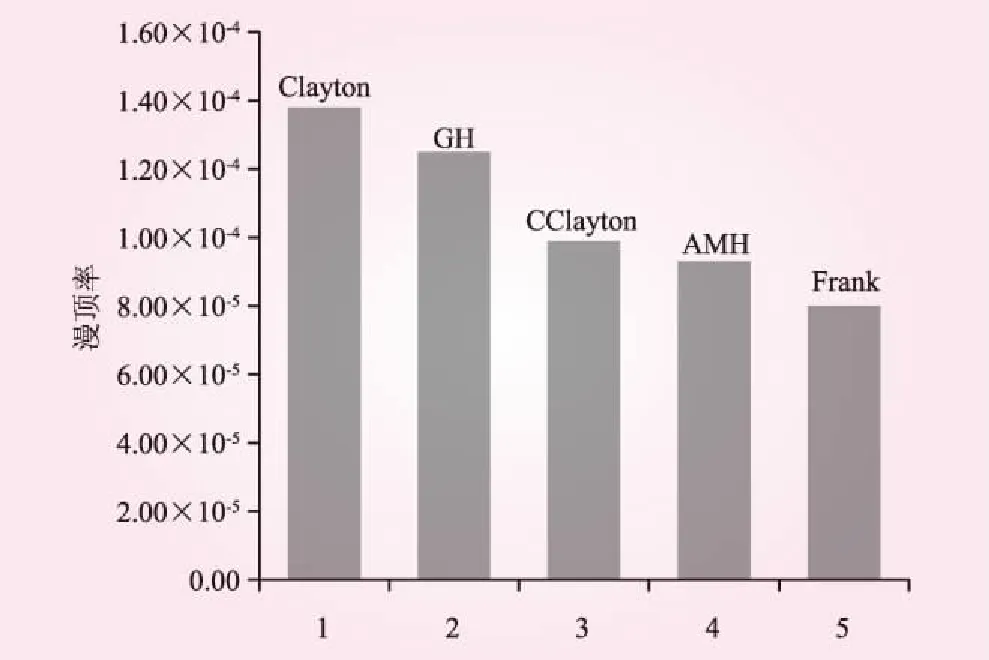
图6 不同Copula函数计算的洪水漫顶率

2.5 不同干支流洪水相关性对洪水漫顶影响

一般而言，干支流洪水变量间往往存在着较弱的正相关性[10-11]，因此，本文主要讨论τ=0.1，0.2，0.3，0.4，0.5等5种干支流洪水相关情况对洪水漫顶的影响。图7分别给出基于Clayton Copula函数的五种不同干支流洪水相关性下的坝上水位累积分布曲线，相应的洪水漫顶风险率计算结果见图8。由图7可以看出，当τ=0.1时，坝上水位累积分布曲线位于最上端，当τ=0.5时，累积分布曲线位于最下端，也就是说随着干支流洪水相关性的增强，漫顶率也在增加。因此在干支流洪水共同作用下的水利工程设计中，若忽略干支流洪水间的相关性，将会低估洪水漫顶风险，使得工程偏危险。

图7 不同干支流洪水相关性坝上水位累积分布曲线

图8 不同干支流洪水相关性的洪水漫顶风险率

3 结 论

本文以桂平航运枢纽为例，采用Copula-Monte Carlo模拟方法构建干支流洪水作用下大坝的洪水漫顶率计算模型，并分析不同Copula函数、不同干支流洪水相关性对漫顶风险率的影响。得到以下结论：

(1)最优的Clayton Copula计算的洪水漫顶率为1.38×10-4。

(2)由于干支流洪水间相关性较弱，不同Copula函数对洪水漫顶的影响并不很明显，GH、CClayton、AMH、FrankCopula均会低估洪水漫顶风险，从防洪安全角度考虑，采用最优的Clayton Copula计算的洪水漫顶率更合理。

(3)随着干支流洪水流量相关性的增强，洪水漫顶率也会相应的增大，若忽略干支流洪水间的相关性，将会低估洪水漫顶风险，使得工程偏危险。