Transport properties of topological nodal-line semimetal candidate CaAs3under hydrostatic pressure∗
2019-04-13JingLi李婧LingXiaoZhao赵凌霄YiYanWang王义炎XinMinWang王欣敏ChaoYangMa麻朝阳WenLiangZhu朱文亮MoRanGao高默然ShuaiZhang张帅ZhiAnRen任治安3andGenFuChen陈根富
Jing Li(李婧),Ling-Xiao Zhao(赵凌霄),Yi-Yan Wang(王义炎),Xin-Min Wang(王欣敏),Chao-Yang Ma(麻朝阳),Wen-Liang Zhu(朱文亮),Mo-Ran Gao(高默然),Shuai Zhang(张帅),Zhi-An Ren(任治安),3and Gen-Fu Chen(陈根富),3,†
1Institute of Physics and Beijing National Laboratory for Condensed Matter Physics,Chinese Academy of Sciences,Beijing 100190,China
2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China
3SongShan Lake Materials Laboratory,Dongguan 523808,China
1.Introduction
The discovery of topological semimetals(TSMs)has attracted broad attention in condensed matter physics and material science because of the topologically protected band structure.TSMs give rise to some exotic physical properties,including giant magnetoresistance(MR),ultrahigh carrier mobility,nontrivial Berry phase,and negative longitudinal MR.[1–4]According to the degeneracy of the band crossing points and their distribution in the Brillouin zone(BZ),TSMs can classify into Dirac semimetals(DSMs),Weyl semimetals(WSMs),and nodal-line semimetals(NLSMs).[5]The band crossing points are four-fold degenerate for DSMs,such as Na3Bi and Cd3As2.[6–8]WSMs exhibit two-fold degenerate band crossing points with definite chirality,and it is located at an even number of discrete points in the BZ,such as TaAs[9,10]and WTe2.[11,12]Different from the discrete points in DSMs and WSMs,the band crossing points form closed loops in the BZ of NLSMs.[13,14]
Recently,it has been reported that black phosphorus(BP)exhibits a topological phase transition from band semiconductor to zero-gap Dirac semimetal state[15,16]under hydrostatic pressure. The semimetal phase in BP is characterized by the large MR,the coexistence of electron and hole pockets,low carrier densities,small cyclotron masses,weak localization-weak antilocalization transition at low magnetic fields and the emergence of a nontrivial Berry phase of π detected by Shubnikov-de Haas(SdH)magneto-oscillations.BP has a puckered honeycomb lattice,[17–19]in which the direct band gap is mainly determined by the out-of-plane pzlike orbital of P and can be further reduced by tuning the interlayer coupling.[15,20,21]Interestingly,in CaAs3,the twodimensional infinite polyanionic As23−nets are derivatives of the BP structure.While a deeper and systematic study on CaAs3single crystals is still missing except for the semiconducting behavior.[22,23]More recently,CaAs3was predicted theoretically to be a candidate for topological insulator(TI)or NLSMs when the spin–orbit coupling(SOC)was taken into consideration or not and the topological transition could be engineered via strain,or chemical doping.[5,24]While it should be degenerate to a strong topological insulator(TI)with taking the SOC into consideration.[5,24]Hydrostatic pressure has been recognized as a powerful tool for studying band structures of semiconductors.Therefore,combined with the theoretical prediction,it is necessary to study the pressure effect on the transport properties of CaAs3.
In this work,we have grown the single crystals of CaAs3and performed the studies of transport properties at atmospheric and hydrostatic pressures.CaAs3shows a semiconducting-like behavior at atmospheric pressure. A large hump in the resistivity is also observed for some crystals containing tiny defects or impurities.Hydrostatic pressure can effectively reduce its resistivity,but it is not fully metallized up to 2 GPa.However,a small drop of resistivity is observed above 1.5 GPa for some samples,indicating the onset of superconducting transition.
2.Experiment and method
Single crystals of CaAs3were grown by the modified Bridgman method.Firstly,stoichiometric amounts of Ca and As granule were put into an Al2O3crucible,and sealed in an evacuated quartz ampule,which was then heated extremely slowly and kept at 900◦C for 10 h before turning the furnace off.Secondly,the precursor was grinded,tableted,put into an Al2O3crucible,and then sealed again as described in the first step.The quartz ampule was heated to 800◦C,kept at this temperature for 50 h,and then cooled to 400◦C slowly.The phase of obtained single crystals was characterized by xray diffraction(XRD)on a PANalytical diffractometer with Cu Kα radiation at room temperature and atmospheric pressure.The elemental compositions were checked by Oxford XMax energy dispersive x-ray(EDX)spectroscopy analysis in a Hitachi S-4800 scanning electron microscope. Electrical resistivity was measured by the conventional dc four-probe method and the measurements were performed on a Quantum Design physical properties measurement system(PPMS-9).Samples were pressurized in a piston cylinder device made of Be–Cu alloy.The pressure transmitting medium was Daphene Oil 7373.The pressure inside the device was determined by shifting the superconducting transition temperature of Pb strip.
3.Results and discussion
In Fig.1(a),the powder XRD pattern of CaAs3can be well indexed to the triclinic P1¯ structure with the lattice parameters a=5.88(1)A˚,b=5.85(1)A˚,and c=5.93(1)A˚,α =70.05(1)◦,β =80.16(1)◦,and γ=75.83(1)◦,which are in agreement with the previous reported values.[25]Figure 1(b)shows the single crystal XRD pattern of the CaAs3.All of peaks can be identified as the(0k0)reflections.For comparison,we also show the crystal structure of BP in Fig.1(c).BPis a two-dimensional(2D)layered material which is stacked together by weak van der Waals force.Each P atom is covalently bonded with three adjacent P atoms to form a puckered honeycomb structure in a single layer.One can clearly see that the crystal structure of CaAs3is similar to that of BP.Here CaAs3can be viewed as a list of 2D infinite puckered polyanionic layers As23−
stacking along the b-axis and Ca2+cations are inserted into the interstitial sites,in which the puckered arsenic layers are directly derived from the orthorhombic structure of BP by removing 1/4 of the P atoms in an ordered way.[23]
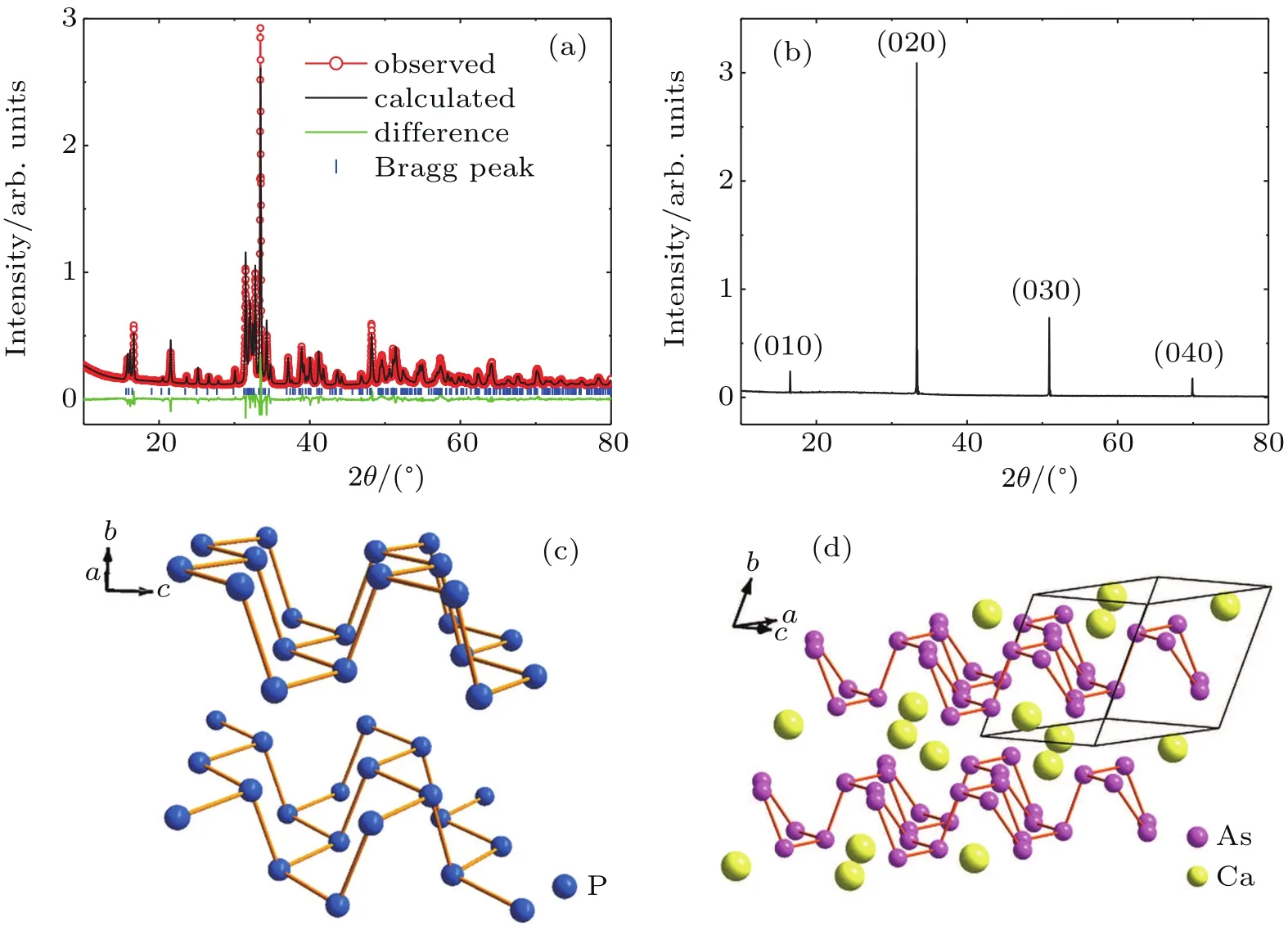
Fig.1.(a)Powder XRD pattern of CaAs3obtained by grinding the single crystals at room temperature and the refinement results.(b)The single crystal XRD of CaAs3.(c)and(d)The crystal structure of BP and CaAs3,respectively.
All the samples we measured were taken from different parts of a large crystal of CaAs3.We find that the transport properties show a large sample dependence.The crystals peeled from the bottom exhibit semiconducting-like behavior,while some crystals taken from the top show“bad metal”behavior with a big hump at the temperature T1,as shown in Figs.2(a)and 2(b),respectively.It is noted that the absolute value of resistivity is essentially same between samples#1 and#2 at 300 K.In Fig.2(a),the ρ(T)in the range from 195 K to 265 K can be fitted by Arrhenius equation,ρ = ρ0exp(Eg/kBT),where kBis the Boltzmann constant.The estimated activation energy Egis∼73 meV,which is consistent to the previous report.[22]
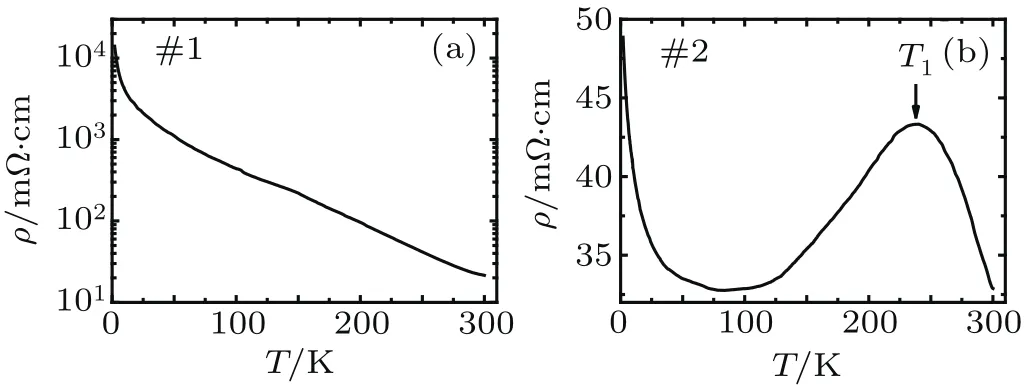
Fig.2.Resistivity ρ plotted as a function of temperature T measured on#1 crystal(a)and#2(b)at atmospheric pressure,respectively.
To further distinguish between the two type resistivity behaviors in the single crystals(#1 and#2)of CaAs3,we performed the Hall-effect measurements at various temperatures on the same samples,as shown in Figs.3(a)and 3(d),respectively.The magnetic field is applied perpendicular to the acplane.Figure 3(a)presents the magnetic field dependence of the Hall resistivity ρxyof the crystal(#1)at several temperatures from 2 K to 300 K.The slope of the ρxycurve is all negative,suggesting that the main carriers should be electrontype.One can find that the ρxyshows nonlinear behavior at 2 K,indicating the coexistence of two types of carriers at very low temperatures.[8,9]Different from sample#1,the slope of ρxyfor sample#2 changes from negative to positive with decreasing temperatures,as shown in Fig.3(d),indicating the transition from electrons dominated transport to holes dominated transport in this sample.All these show that CaAs3is a multiband system.We try to fit the Hall data obtained at 2 K for sample#1 using the semi-classical two-band model,in which Hall conductivity σxycan be expressed as the following equation:[26]

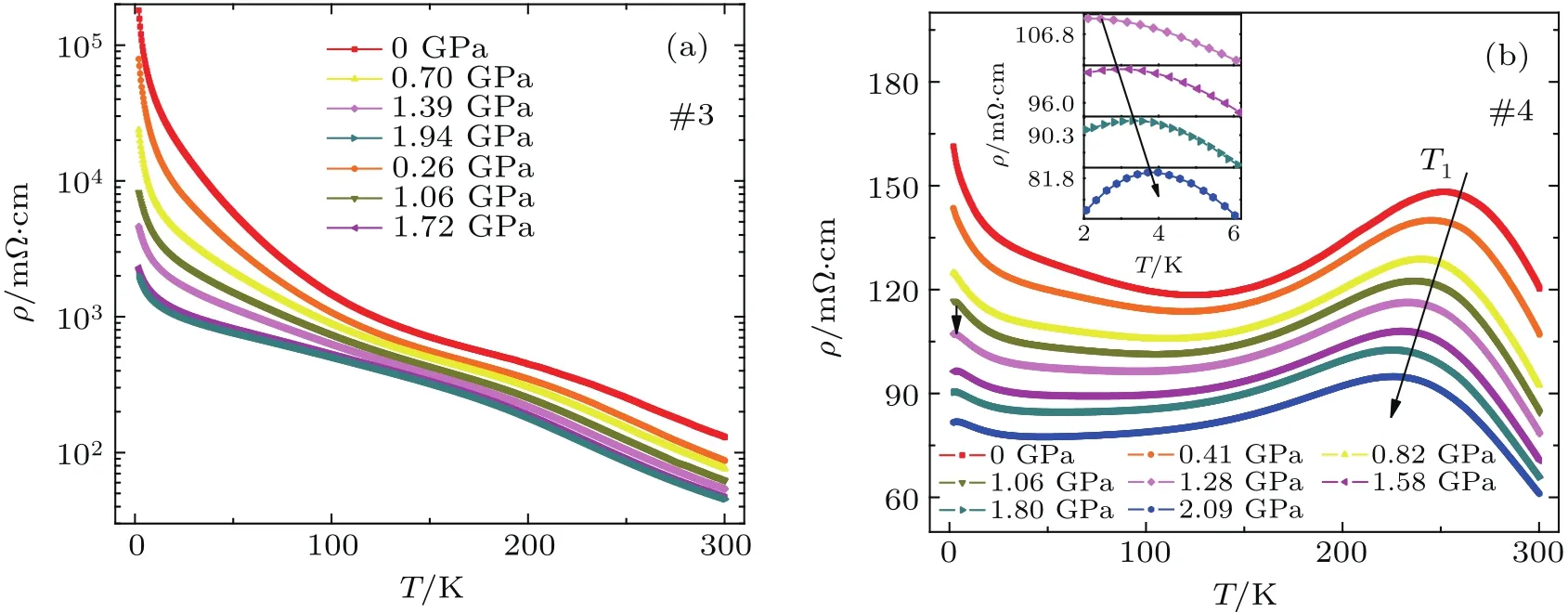
where nh(or ne)is the carrier density of the holes(or the electrons)andµh(orµe)is the mobility of the holes(or the electrons),respectively.For high temperatures,the ρxyappears to be approximately linear,and fitting with two-band model could bring uncertainty.Hence,we use the single-band model to estimate the carrier density nt=1/eRH,and carrier mobility µt=RH/ρ(0 T),where t=e,h indicate electrontype and hole-type carriers,respectively,and the Hall coefficient RHis estimated by the slope of ρxy(B)at low fields(−1 T CaAs3was predicted to hold engineered topological phase transitions by applying external tensile or compressive strains.[24]In order to test the pressure effect of CaAs3,we use the piston cylinder device to apply compressive strains to two samples#3 and#4 which are selected with two typical transport behaviors.Figures 4(a)and 4(b)display the temperature dependence of the resistivity ρ(T)under varying hydrostatic pressures for samples#3 and#4,respectively.The values of ρ(T)both for samples#3 and#4 decrease in its entirety under pressure.At low temperatures,the ρ(T)both for two samples changes more significantly,but not metallized up to 2 GPa.In Fig.4(b),the peak temperature,T1,also shifts to lower temperatures with increasing pressure,while we find that ρ(T)of sample#4 drops with the lowering temperature above 1.5 GPa as shown in the inset.The transition moves to higher temperature with the increasing pressure.It seems natural to ascribe this drop to the onset of superconductivity in such “doped”sample,which provides the possibility for CaAs3to realize a topological nodal-line semimetal or even topological superconductivity under much higher pressure in the future work. Fig.3.(a)and(d)The magnetic field dependence of Hall resistivity ρxyon samples#1 and#2 at various temperatures,respectively.(b),(c),(e),and(f)The temperature dependence of carrier mobilities and carrier densities of electrons and holes measured on samples#1 and#2,respectively. Fig.4.(a)and(b)Resistivity ρ of CaAs3plotted as a function of temperature T on#3 and#4 crystals at various hydrostatic pressures,respectively.Inset of(b):Resistivity ρ above 1.2 GPa in the low temperature region(2 K–6 K). In summary,we have synthesized the single crystals of CaAs3,which has been predicted to be a topological nodal-line semimetal candidate.CaAs3shows an n-type semiconductinglike behavior at atmospheric pressure.While for some samples with the presence of crystal defect and/or impurities,the resistivity shows an obvious hump around 230 K,at which the dominated carriers change from hole-type to electron-type.The application of hydrostatic pressure results in decrease of the resistivity for both samples,but they are not fully metallized on the whole.A possible superconducting transition is also observed in some “doped”samples above 1.5 GPa.Our work will provide valuable clues for further exploration of the topological phase in CaAs3,and in-depth studies are needed in future. [1]He J B,Chen D,Zhu W L,Zhang S,Zhao L X,Ren Z A and Chen G F 2017 Phys.Rev.B 95 195165 [2]Weng H M,Dai X and Fang Z 2016 J.Phys.:Condens.Matter 28 303001 [3]Bansil A,Lin H and Das T 2016 Rev.Mod.Phys.88 021004 [4]Chiu C K,Teo J C Y,Schnyder A P and Ryu S 2016 Rev.Mod.Phys.88 035005 [5]Xu Q N,Yu R,Fang Z,Dai X and Weng H M 2017 Phys.Rev.B 95 045136 [6]Xiong J,Kushwaha S K,Liang T,Krizan J W,Hirschberger M,Wang W,Cava R J and Ong N P 2015 Science 350 413 [7]Liu Z K,Zhou B,Zhang Y,Wang Z J,Weng H M,Prabhakaran D,Mo S K,Shen Z X,Fang Z,Dai X,Hussain Z and Chen Y L 2014 Science 343 864 [8]Liang T,Gibson Q,Ali M N,Liu M H,Cava R J and Ong N P 2015 Nat.Mater.14 280 [9]Huang X C,Zhao L X,Long Y J,Wang P P,Chen D,Yang Z H,Liang H,Xue M Q,Weng H M,Fang Z,Dai X and Chen G F 2015 Phys.Rev.X 5 031023 [10]Zhang C L,Xu S Y,Belopolski I,Yuan Z J,Lin Z Q,Tong B B,Bian G,Alidoust N,Lee C C,Huang S M,Chang T R,Chang G Q,Hsu C H,Jeng H T,Neupane M,Sanchez D S,Zheng H,Wang J F,Lin H,Zhang C,Lu H Z,Shen S Q,Neupert T,Hasan M Z and Jia S 2016 Nat.Commun.7 10735 [11]Soluyanov A A,Gresch D,Wang Z J,Wu Q S,Troyer M,Dai X and Bernevig B A 2015 Nature 527 495 [12]Cai P L,Hu J,He L P,Pan J,Hong X C,Zhang Z,Zhang J,Wei J,Mao Z Q and Li S Y 2015 Phys.Rev.Lett.115 057202 [13]Burkov A A,Hook M D and Balents L 2011 Phys.Rev.B 84 235126 [14]Weng H M,Liang Y Y,Xu Q N,Yu R,Fang Z,Dai X and Kawazoe Y 2015 Phys.Rev.B 92 045108 [15]Xiang Z J,Ye G J,Shang C,Lei B,Wang N Z,Yang K S,Liu D Y,Meng F B,Luo X G,Zou L J,Sun Z,Zhang Y and Chen X H 2015 Phys.Rev.Lett.115 186403 [16]Li C H,Long Y J,Zhao L X,Shan L,Ren Z A,Zhao J Z,Weng H M,Dai X,Fang Z,Ren C and Chen G F 2017 Phys.Rev.B 95 125417 [17]Rodin A S,Carvalho A and Castro Neto A H 2014 Phys.Rev.Lett.112 176801 [18]Li D A,Jussila H,Karvonen L,Ye G J,Lipsanen H,Chen X H and Sun Z P 2015 Sci.Rep.5 15899 [19]Morita A 1986 Appl.Phys.A 39 227 [20]Takao Y,Asahina H and Morita A 1981 J.Phys.Soc.Jpn.50 3362 [21]Asahina H,Shindo K and Morita A 1982 J.Phys.Soc.Jpn.51 1193 [22]Bauhofer W,Wittmann M,Gmelin E and van Schnering H G 1982 Physics of Narrow Gap Semiconductors(Berlin Heidelberg:Springer)p.30 [23]Bauhofer W,Wittmann M and Vonschnering H G 1981 J.Phys.Chem.Sol.42 687 [24]Quan Y,Yin Z P and Pickett W E 2017 Phys.Rev.Lett.118 176402 [25]Brice J F,Courtois A,Protas J and Aubry J 1976 J.Sol.St.Chem.17 393 [26]Ashcroft N W and Mermin N D 1976 Solid Sate Physics(New York:Holt,Rinehart and Winston) [27]Zhao L X,Huang X C,Long Y J,Chen D,Liang H,Yang Z H,Xue M Q,Ren Z A,Weng H M,Fang Z,Dai X and Chen G F 2017 Chin.Phys.Lett.34 037102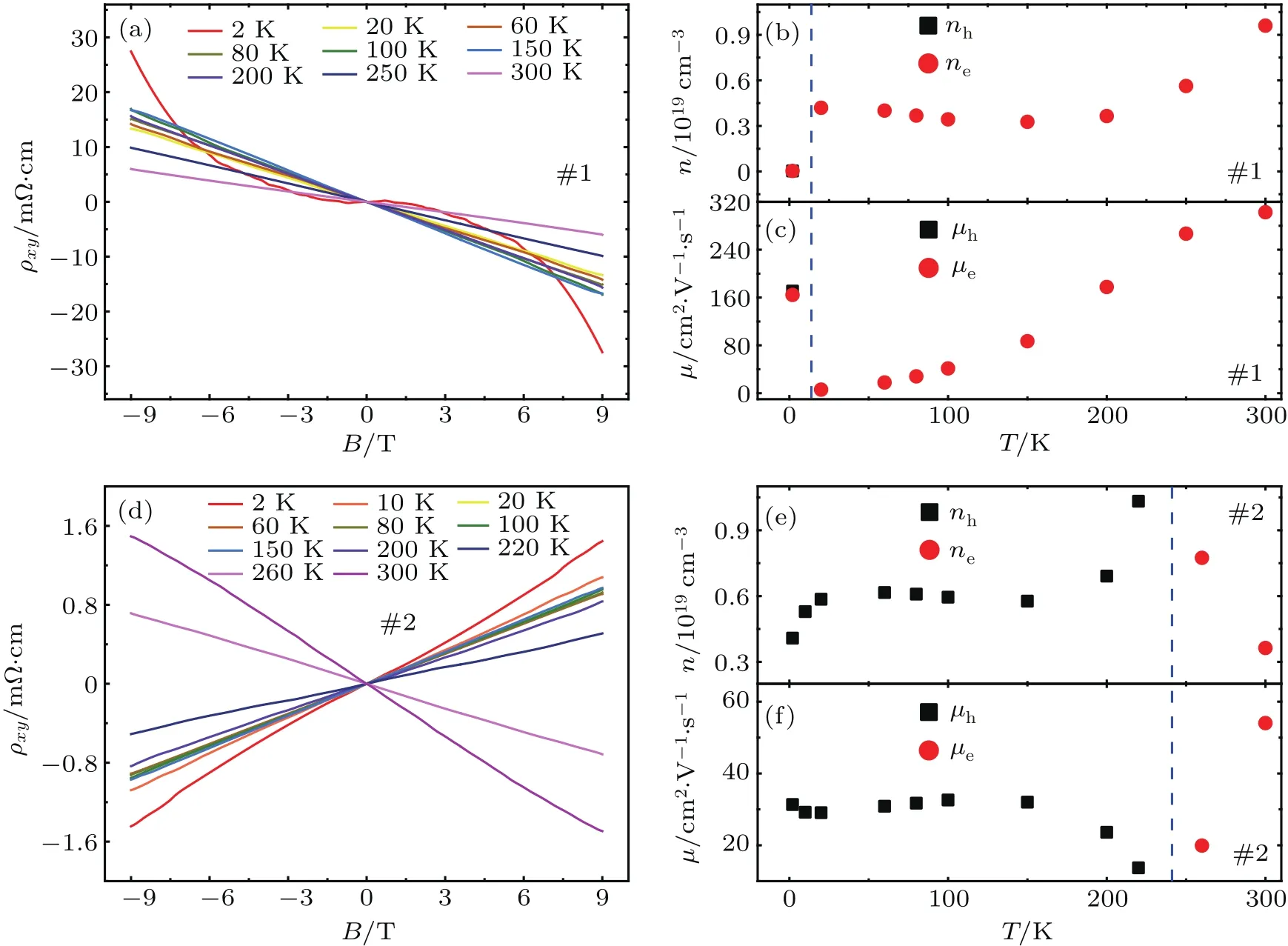
4.Conclusion
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Effect of carrier mobility on performance of perovskite solar cells∗
- Plasma electrolytic liquefaction of sawdust∗
- Insight into band alignment of Zn(O,S)/CZTSe solar cell by simulation∗
- Effect of terahertz pulse on gene expression in human eye cells∗
- Ultraviolet photodetectors based on wide bandgap oxide semiconductor films∗
- A primary model of decoherence in neuronal microtubules based on the interaction Hamiltonian between microtubules and plasmon in the neurons
