预应力锚索锚固段应力分布与锚固段长度研究

高 毅 博

(中国地质大学(武汉)工程学院，湖北 武汉 430074)

1 概述

目前，岩土工程在工程建设中所面临的问题越来越多，对于灾害有着越来越高的要求[1]。在工程防治领域，锚固技术能够充分发挥岩土体的内在强度，且锚固结构较轻，能够有效抑制岩土体的变形，此外，锚固技术工程成本较低，优势较为明显。因此，锚固技术在我国重大工程建设中发挥着越来越重要的作用。

而在进行锚固结构设计时，分析清楚锚固机理是至关重要的。锚固机理的核心问题是寻找锚固体的内力分布规律，因此，国内外学者进行了大量的研究工作，目前主要有剪应力均匀分布[2]、剪应力沿双曲线分布[3]和负指数分布[4]三种模型。然而，现行规范大多数采用剪应力均匀分布这种模型来选择锚固参数，这种锚固设计显然有很多不完善之处，计算的结果往往与实际有较大的出入[5]。

之前学者对于剪应力分布的假设和分析较为复杂，在工程建设中无法得到应用[5]。因此，本文结合弹性理论，将锚固段的受力视为半无限空间体边界上某点受到集中力的作用，对锚索锚固段的内力结构及锚固段长度取值问题进行探究。

2 基本微分方程

2.1 布西涅斯克(Boussinesq)问题的位移解

结合朱训国[6]的假定条件，则全长注浆锚索力学模型可以理解为半无限空间体边界上受一法向集中力P的作用，计算简图如图1所示，不计体力，则空间内某点的位移计算式为：

(1)

(2)

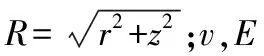
2.2 基本微分方程

(3)

对式(3)进行两次求导可得：

(4)

(5)

根据式(4)，结合式(5)，分析可以得到锚固段沿长度方向的剪应力分布函数，即为式(5)：

(6)

对式(6)沿锚固段长度方向上进行积分，即可得到轴力在锚固段长度上的分布函数，如式(7)所示：

(7)

2.3 锚固段长度

在工程运行期间只要不发生变形破坏，所需满足的条件为锚索所受的外力小于锚索的设计值，即:

(8)

根据式(7)，结合锚索不发生破坏的条件，即可得到锚固长度的设计值，如式(9)所示：

(9)

3 锚固段受力影响因素分析

根据剪应力和轴力沿锚固段长度方向上的分布函数，对锚索锚固段内力分布有影响的是外荷载P、岩土体和锚固体的弹性模量和锚固体的直径等。结合锚固段应力分布的函数，采用文献[7]中的数据，锚固体的半径为0.06 m，岩土体的泊松比μ=0.3，岩土体和锚固体的弹性模量分别为E=3×103MPa,Ep=2.1×105MPa。

3.1 外荷载P的影响

假定对试验锚固系统施加不同级别的外荷载P，P值由小及大为60 kN，80 kN，100 kN和120 kN，计算过程中的其他参数与文献[7]中的参数一致，根据上文中的式(6)和式(7)，可绘制出如下锚固段内力分布曲线。

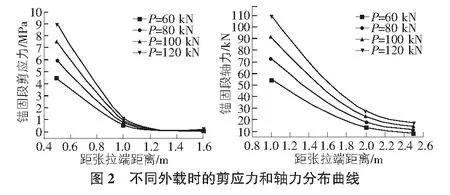
根据图2分析可知，随着外荷载值P的不断增大，剪应力和轴力不断增大，这说明增大预应力外部荷载值在一定程度上可以增强锚固效果，但锚固体轴力的不断增大，表明锚固体受到的拉应力越大，会产生较为明显的应力集中，导致锚固段注浆体容易开裂。同时可以看出，剪应力主要作用范围是一定的，荷载的增大对其影响不大。

3.2 孔径d的影响

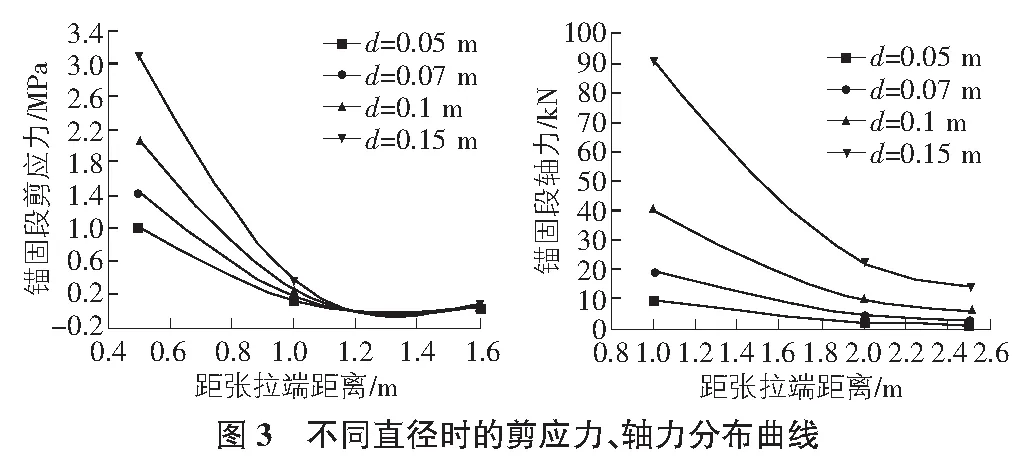
假定对不同孔径的锚固系统施加P=100 kN的荷载，采用当今锚固系统经常采用的几种孔径，孔径d分别为0.05 m,0.07 m,0.1 m,0.15 m，计算过程中的其他参数与文献[7]中的参数一致，根据上文中的式(6)和式(7)，可绘制出如下锚固段内力分布曲线。

根据图3分析可知，沿锚固段的应力分布是不均匀的，且随着锚固段长度的增大，剪应力和轴力不断减小，最大值出现的在顶部位置。说明锚固段的应力分布主要集中在锚固段的顶端，但随着锚固体直径的增大，应力衰减的越快。

3.3 不同弹性模量比值Ep/E的影响

假定对不同弹性模量比值Ep/E的锚固系统施加P=100 kN的荷载，孔径d为0.12 m，Ep/E分别为20,30,40,50，其他参数与算例中参数相同，根据式(6),式(7)可绘制出在不同岩土体时下的锚固段轴力、剪应力分布曲线。

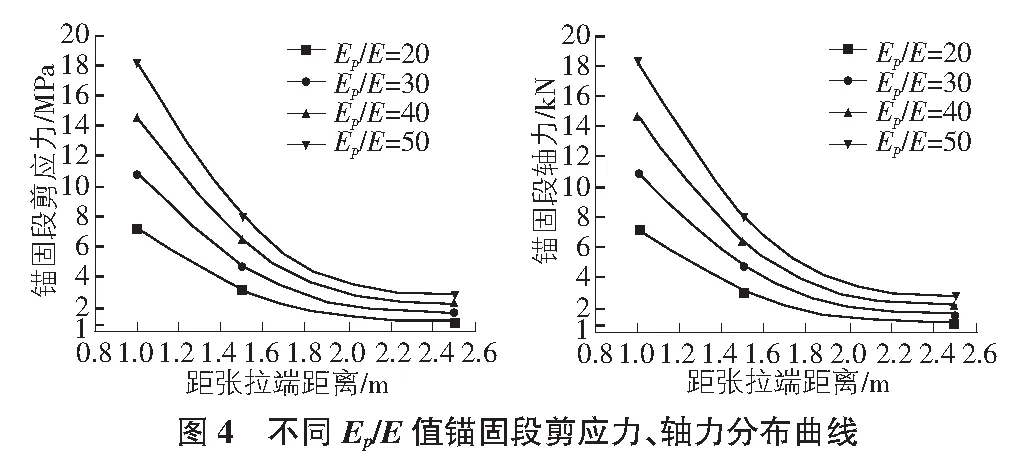
根据图4分析可知，随着Ep/E值的不断增大，沿锚固段的应力衰减速度越快，且随着锚固段长度的增大，剪应力和轴力不断减小，至锚固段远端接近于0，说明Ep/E值越大，锚固段应力曲线分布越不均匀，应力分布的范围越广，且锚固体顶部的剪应力越大，会产生较为明显的应力集中现象，容易导致该锚固系统发生破坏。

3.4 泊松比μ的影响

根据应力沿锚固段长度的分布函数，结合张建超文献可发现，岩土体的泊松比对于锚固段的应力分布影响不是很大，可以忽略。

4 结语

1)运用空间弹性理论，结合布西涅斯克(Boussinesq)问题的位移解推求了锚固段的剪应力和轴力沿锚固段的分布函数，并提出了锚固段长度的计算公式，为之后锚固系统的设计提供了一种理论依据。

2)在锚固系统中，对锚索锚固段内力分布有影响的是外荷载P、岩土体的和锚固体的弹性模量比值Ep/E和锚固体的孔径d等。锚固段的应力大小与外荷载P和锚固体孔径d正相关，而锚固体与岩土体的弹性模量比值Ep/E影响着锚固段应力分布的均匀程度。锚固段最大应力值与Ep/E值正相关。

3)在锚固系统中，过长的锚固段长度并不能改善锚固性能。

4)本文的方法是基于弹性理论，假设的内容较为理想，与实际工程建设存在一定的差距，因此，在今后的学习和研究中，对该问题仍需改善。