基于区间直觉模糊信息TODIM法的水利工程应急决策研究*

孙开畅，陈 璇，时训先，马文俊，朱自立

(1.三峡大学 水利与环境学院，湖北 宜昌 443002； 2.中国安全生产科学研究院 工业安全研究所，北京 100012)

0 引言

水利工程多处于高山峡谷地带，施工过程中不可预见因素较多，安全事故时有发生。随着对安全生产的高度重视，水利工程安全事故总体呈现下降趋势，但发生总量仍旧偏大[1-2]。水利工程事故的发展演变面临多种情景，如何在最短时间内选择出最优的应急方案，最大限度地减少人员伤亡和财产损失，已成为水利工程应急管理中的关键问题[3]。

陈孝国等[4]针对煤矿突发事件应急救援，提出基于直觉模糊集的TOPSIS群决策方法；马文笑等[5]将本体模型与案例推理结合，建立了“情景-应对”的应急决策模型；郑霞忠等[6]针对水电厂突发事件特点建立了应急救援方案云决策模型；樊治平等[7]针对突发事件发展演变存在的不同情形，提出了基于前景理论的应急响应风险决策方法；江新等[9]针对水电工程施工突发事件，建立了基于前景理论及云模型的应急决策方法。以上研究虽然考虑了决策环境的模糊性，但很少考虑决策者的心理行为[4-6]，有些研究虽然考虑了这一点[7-10]，却未考虑决策者的风险态度，影响决策结果的有效性和准确性。TODIM方法[11]是在考虑决策者心理行为的基础上选择接近决策者偏好的决策方法，相对于传统的前景理论方法，该方法不需要设置参照点，能较完整地保留决策信息。鉴于此，笔者针对水利水电工程应急决策的特点，将决策环境的模糊性和决策者的心理行为及风险态度相结合，建立基于区间直觉模糊集和TODIM方法的决策模型，并通过不同区间直觉距离测度公式验证模型的鲁棒性，以期提高水利工程应急决策的科学性和合理性。

1 水利工程安全事故应急决策特点分析

水利工程安全事故应急处置涉及技术事故、自然灾害(引发)、环境保护、公共卫生和人为突发事件等多个公共安全领域，是1个复杂的系统，进行科学及时的应急决策要求决策群体具备较强的能力。水利工程的特殊性导致应急决策有如下特点：

1)水利工程应急决策面临的形势严峻，时间紧迫，决策者需要在有限的时间内处理繁杂的信息，尽快选择并启动最符合实际情况的应急预案。

2)水利工程安全事故具有突发性、多样性和严重性等特点，一旦启动应急响应，决策者面临的决策压力较大，心理负担随之增加。在复杂的决策环境下，决策者的心理行为和风险态度是决策的重中之重。

3)水利工程应急决策是典型的非程序决策。决策程序应在不损害决策合理性的前提下适当简化，以提高决策效率。

4)水利工程安全事故具有多阶段不确定性。由于水利工程安全事故的发生、演变的过程不确定，应急决策应随着事态发展而变化，以适应复杂的环境，提高整个应急处置的效果。

5)水利工程受社会关注度高，应急决策应当重视社会影响，将之与救援时效性、经济性等结合考虑。

水利工程安全事故应急决策流程如图1所示。

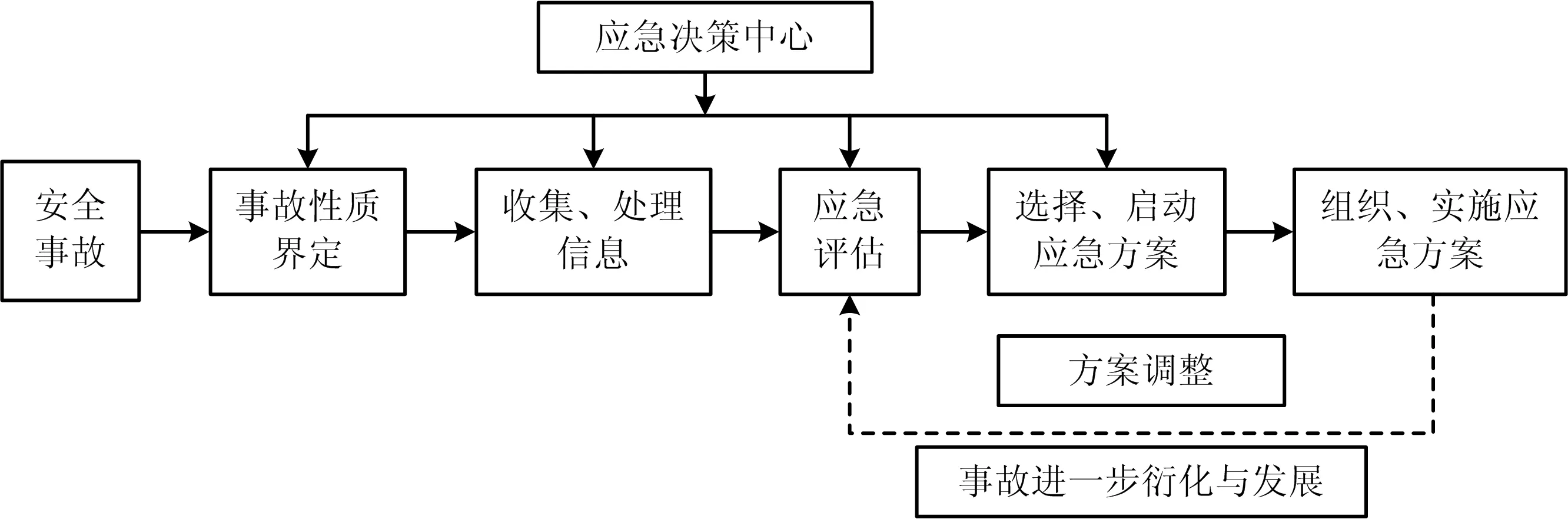
图1 水利工程安全事故应急决策流程Fig.1 Flow chart of emergency decision-making for safety accidents in water conservancy projects

2 区间直觉模糊集

由于客观事物的复杂性和不确定性，直觉模糊集中的隶属度和非隶属度的值往往难以用精确的实数值来表达，而用区间数则比较合适，更能刻画复杂决策环境下决策者的心理犹豫状态。Atanassov等[12]对直觉模糊集进行了扩展，提出了区间直觉模糊集的定义。

定义1.1[13]：设X=(x1,x2,…,xn)是1个非空集合，A={(x,μA(x),vA(x)|x∈X)}为区间直觉模糊集，其中μA(x)和vA(x)分别表示X中元素x属于A的隶属度和非隶属度，μA(x)∈[0,1]，γA(x)∈[0,1]，x∈X，且满足条件：

(1)

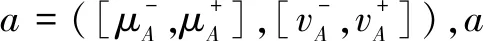
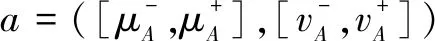
(2)

式中：S为a的得分函数，S(a)∈[-1,1]。

为有效测度区间直觉模糊数的差异程度，徐泽水[15]对常见的区间直觉模糊距离测度进行了总结，包括几种重要的距离测度公式：

1)标准的Hamming距离

(3)

2)标准的Euclidean距离

(4)

3)基于Hausdorff测度的标准的Hamming距离

(5)

4)基于Hausdorff测度的标准的Euclidean距离

(6)

3 区间直觉模糊TODIM决策模型

TODIM法是Gomes等[16]在前景理论的基础上，提出的1种既充分考虑决策者心理行为又不需要确定参照点的方法，该方法通过计算备选方案与其他方案的相对优势度进行方案比较排序。在实际决策过程中，为客观表达事故应急处理的实际信息，本文引进区间直觉模糊集理论，结合TODIM方法建立符合决策者心理状态的应急决策模型。

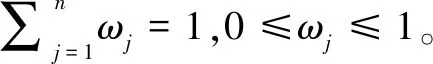
1)邀请决策专家小组对备选方案进行评价，得到决策矩阵X=[xij]m×n，并将决策矩阵规范化为标准矩阵Y=[yij]m×n，挖掘决策矩阵信息，运用区间直觉模糊熵计算得出各属性的权重及相对权重。

区间直觉模糊熵定义[17]为：

(7)

属性Cj权重和相对权重分别为：

(8)

(9)

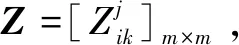
(10)

3)计算方案Ai在属性Cj下相对于方案Ak的占优度Φj(Ai,Ak))：

(11)

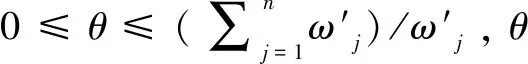
根据占优度矩阵，计算方案Ai对Ak的总体占优度Φ(Ai,Ak)，公式如下：

(12)

4)综合计算方案Ai相对于其他方案的总体占优度S(Ai)，根据S(Ai)大小进行排序：

(13)

4 实例分析

某集团施工队混凝土班在进行泄洪洞施工时突发山体滑坡，洞口值班室被滑下的4 000多m3土石及树木全部埋没。施工队长立即上报情况，不久，洞口再次滑坡，洞口被全部堵塞。经过6 h的抢救，有4位遇难职工的遗体被挖出。事故发生后，工程项目部联合各单位根据《水利工程建设重大质量与安全事故应急预案》，按事故的影响范围和严重性，确定此次事故应急响应级别为III级，并立即启动了生产安全应急救援预案。经初步判断迅速制定了5套应急救援方案A1～A5，应用本文提出的决策模型对应急救援方案进行决策分析。在滑坡救援过程中，为了高效有序地进行救援行动，首先要考虑救援工作的时效性，做好各类救援准备工作，妥善处理救援过程中的各种意外事故。为了避免山体二次滑坡完全堵塞洞口，需对灾害现场进行监测控制，及时搜集现场情况；在救援工作中需使用各种型号的掘进机械，在黄金时段内进行持续高效的挖掘。从社会影响的角度考虑，要尽全力做好善后恢复工作，降低灾害所造成的社会影响。针对工程实际情况，综合考虑水利工程施工作业和山体滑坡应急救援的特点，遵循系统性、科学性、可操作性、普遍性与特殊性的原则，从已建立的水利工程综合应急能力指标体系[18]中筛选出部分重要指标，并通过工程现场技术人员及安全生产专家对指标进行筛选，得到该事故应急救援方案优选指标，如表1所示。专家组根据表1对应急方案A1～A5进行评价，得到区间直觉模糊决策矩阵，如表2所示。

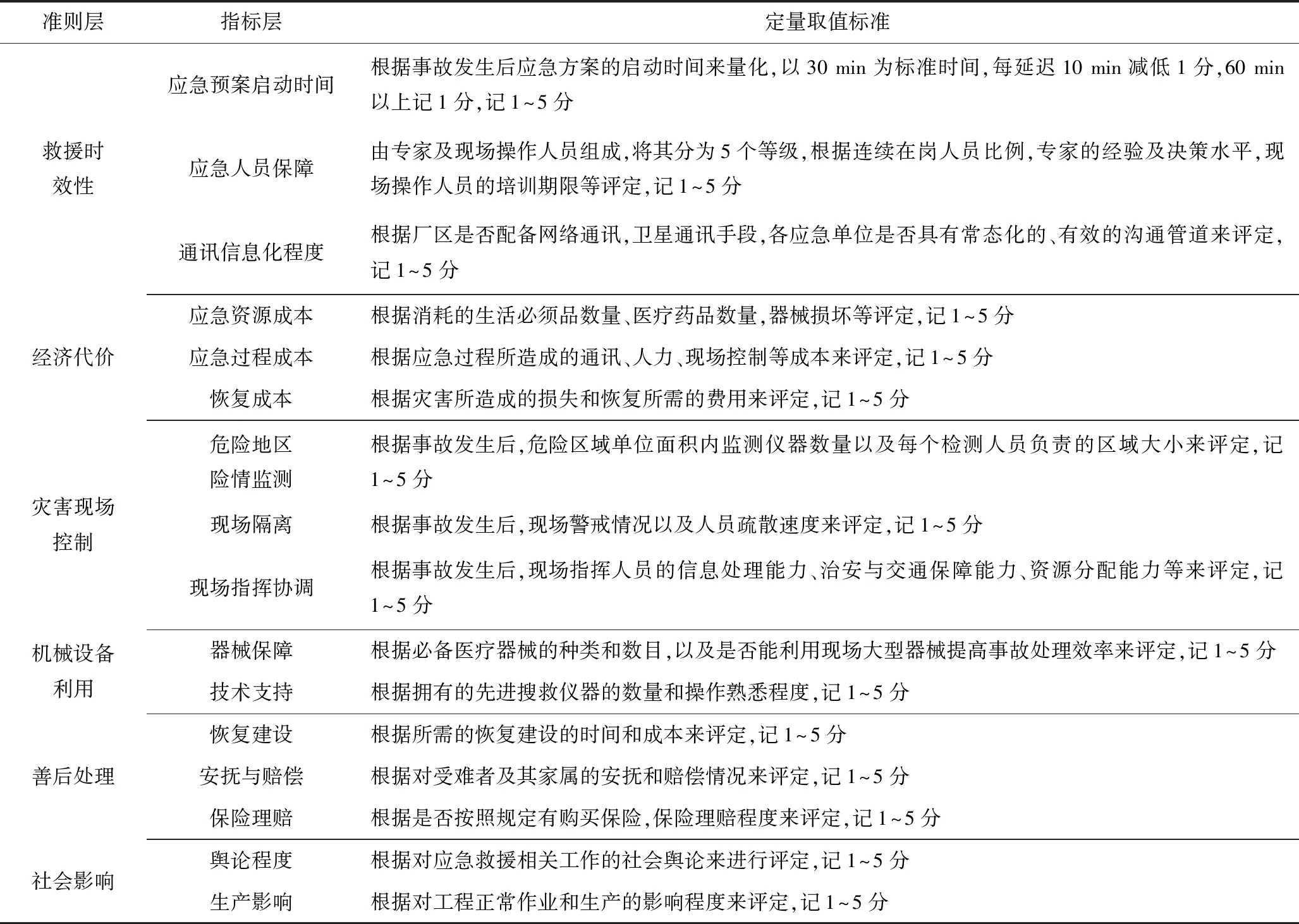
表1 水利工程应急救援方案优选指标Table 1 Index table of emergency rescue plan for water conservancy project

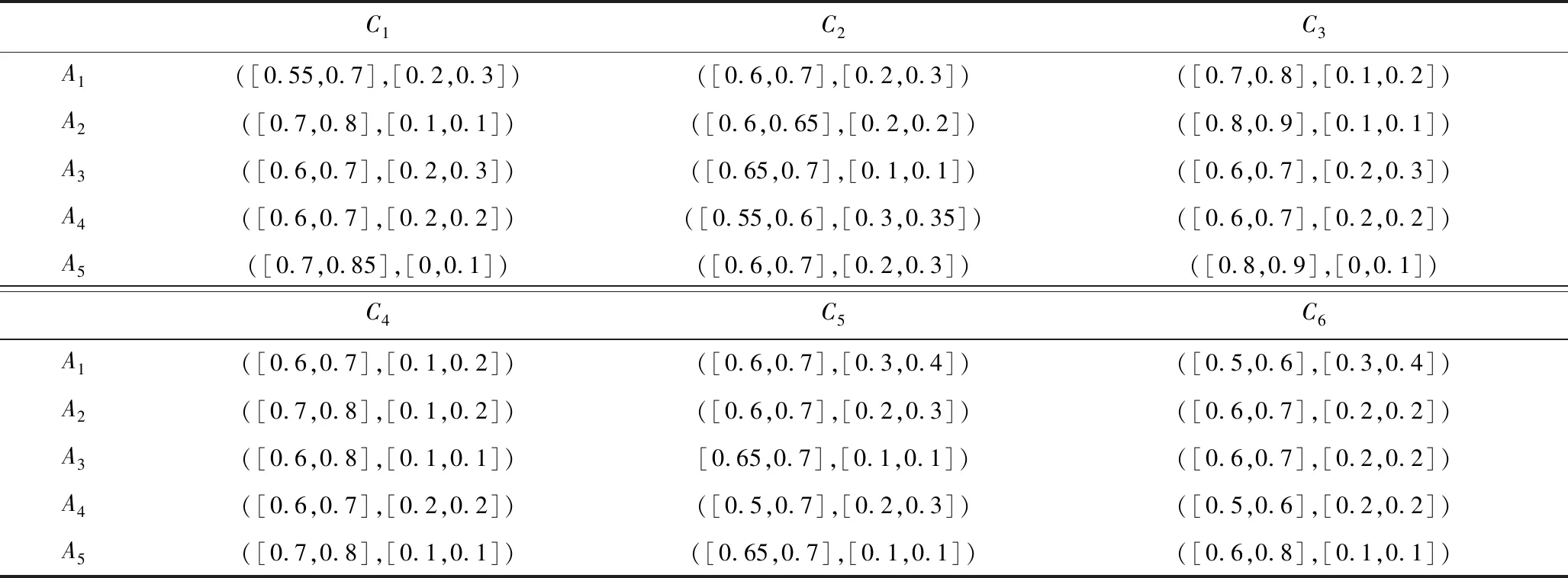
表2 区间直觉模糊决策矩阵Table 2 Interval intuitionistic fuzzy decision-making matrix

由式(7)～(8)计算各属性权重及相对权重分别为：ω=(0.174，0.147，0.197，0.184，0.143，0.155)，ω′=(0.750，1,0.933，0.730，0.788)；将区间直觉模糊决策矩阵化为标准矩阵，运用4种区间直觉模糊距离测度公式(式(3)～(6))，求得各属性Cj下方案两两比较的损益值。通过式(11)～(12)分别计算各方案相对占优度和总体优势度，θ=(0.3,0.8,1.0,2.5,3.0,4.0) ，计算结果如表3所示。

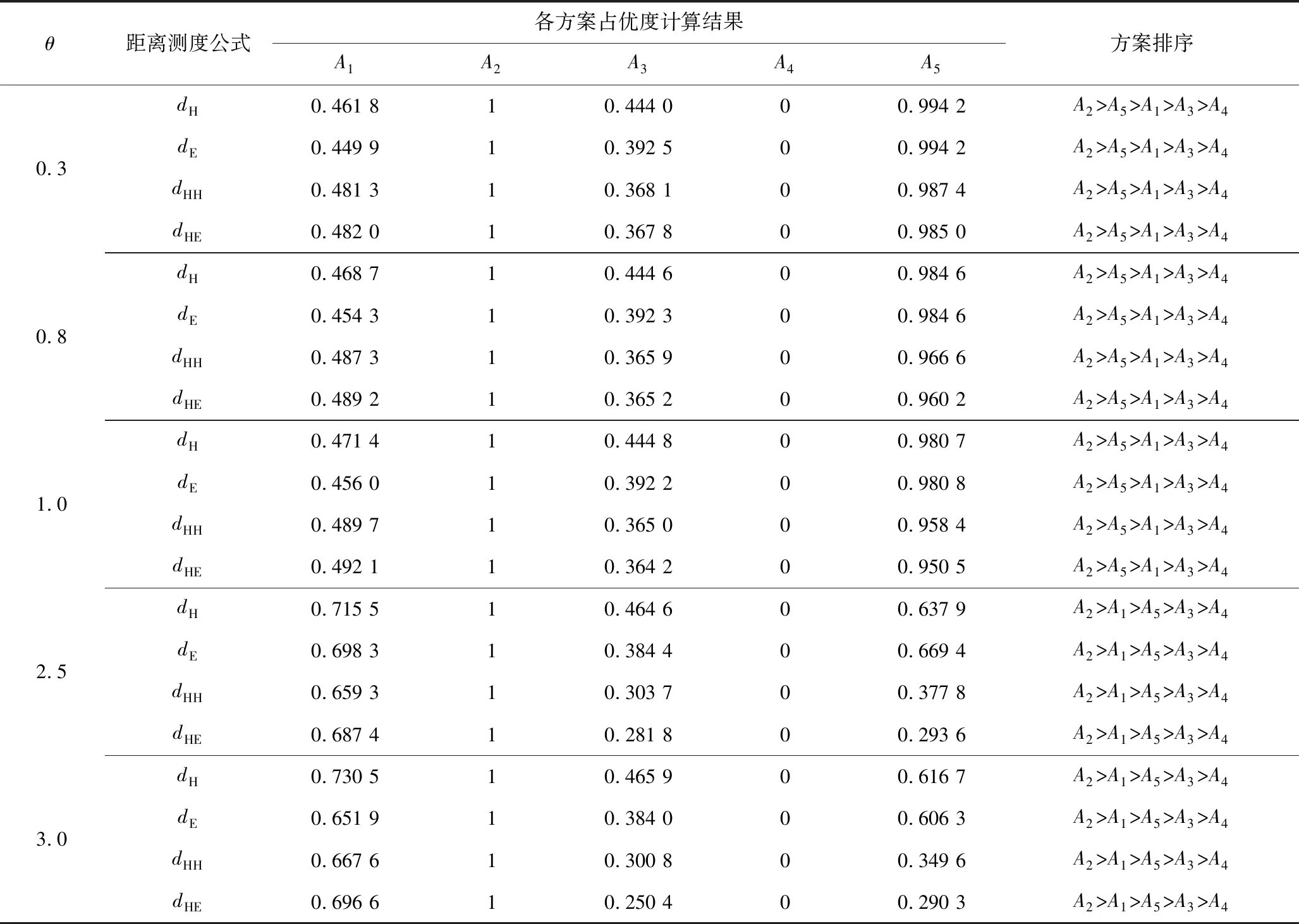
表3 不同θ下备选方案在4个距离公式下的占优度比较结果Table 3 The comparison results of the alternative dominance in the four distance formulas whenθ varies

表3(续)

通过计算可知，在参数θ确定的情况下，采用4种经典的区间直觉模糊距离公式计算并未影响备选方案结果排序，决策结果具有一定的鲁棒性。随着θ的增大，即决策者对待风险态度的变化，备选方案排序也发生了明显的变化。在θ较小时，备选方案A2，A5为优选方案；随着θ的增大，优选方案变为A2，A1。在实际水利工程事故中，若事故现场不稳定，抵御风险能力较弱，在使用本模型计算时可选取较小θ值；若事故现场情况较稳定，则可以选择较大的参数θ。研究结果表明：基于区间直觉模糊信息的TODIM方法可根据决策者的风险态度动态调整应急方案，且决策结果相对稳定。

5 结论

1)基于水利工程安全事故的特点及其应急能力特性，充分考虑到决策环境的不确定性及决策者的心理行为，构建了考虑决策者风险偏好的水利工程应急决策模型。

2)区间直觉模糊集的TODIM决策方法不仅充分考虑了决策者的心理因素及主观偏好对决策结果的影响，且不需要确立参照点计算备选方案的前景价值，只需通过方案两两比较计算相对占优度进行综合评价，简化了决策过程，提高了决策效率。

3)经典的区间直觉模糊距离测度公式对TODIM决策结果具有一定鲁棒性，验证了该模型具有一定的可靠性和稳定性。同时，可通过改变风险规避系数得到不同事故情景下的应急决策结果，使得该模型具有很好的适用性。