对有心圆锥曲线一组性质的研究

辽宁省沈阳北软信息职业技术学院计算机系2017 级软件5 班(110136) 刘新飞(学生)

辽宁省黑山县第一高级中学(121400) 刘大鹏

图1

笔者拜读文[1]受益匪浅并对该题进行更深入研究得到有心圆锥曲线的一组性质.以下是探究过程：

把数据一般化,探究定值的表达式,得到：

定理1 如图已知椭圆点B,C分别是椭圆O的上下顶点,点P是直线l∶y=-a上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.已知BM,BP的斜率分别为k1,k2,则k1k2为定值.

证明设P(x0,-a),联立

消y,得

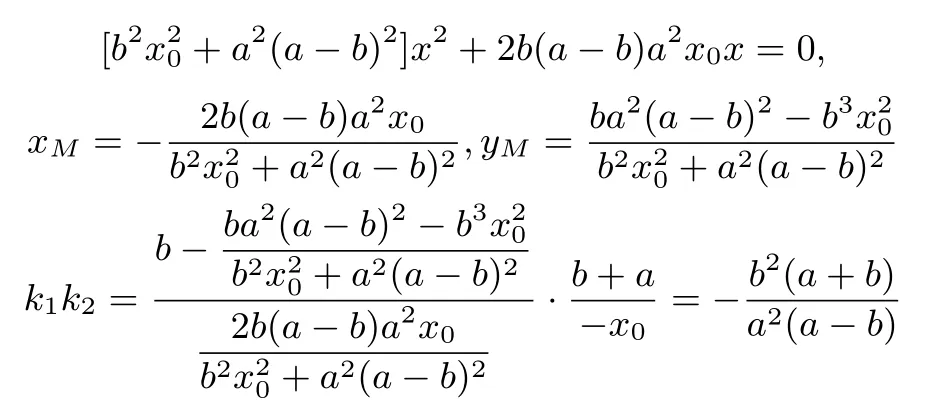
为定值.

改变直线l的位置,探究定值的表达式,得到：

定理2 如图已知椭圆点B,C分别是椭圆O的上下顶点,点P是直线l∶y=上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.已知BM,BP的斜率分别为k1,k2,则k1k2为定值.

证明设P(x0,-λa),联立消y,得[b2x20+a2(λa-b)2]x2+2b(λa-b)a2x0x=0,为定值.

将B换成长轴端点,直线l换成垂直于x轴的直线,得到：

定理3 如图2 已知椭圆点B,A分别是椭圆O的左右顶点,点P是直线上的一个动点(与x轴交点除外),直线PB交椭圆于另一点M. 已知AM,AP的斜率分别为k1,k2,则k1k2为定值.

图2

证明设P(λb,y0),联立消x,得[a2y20+b2(λb+a)2]y2-2ab2(λb+a)y0y=0,为定值.

将研究对象换成双曲线,得到：

定理4 如图3已知双曲线点B,A分别是双曲线O的左右顶点,点P是直线上的一个动点(与x轴交点除外,过B与渐近线平行的直线与l的交点除外),直线PB交双曲线于另一点M. 已知AM,AP的斜率分别为k1,k2,则k1k2为定值.

图3

证明设P(λb,y0),联立消x,得[-a2y20+b2(λb+a)2]y2-2ab2(λb+a)y0y=0,

为定值.

下面探究抛物线y2=2px是否具有类似性质.

已知抛物线y2=2px,点是直线l∶x=上的一个动点(与x轴交点除外),直线PO交抛物线于另一点M.A(x0,0),已知AM,AP的斜率分别为k1,k2,探究：k1k2能否为定值.

与P和A的位置有关,不是定值.所以抛物线不具有类似性质.

以上探究过程说明将问题一般化,并应用类比的方法由此及彼是研究圆锥曲线性质的很好方法,他能最大限度开发试题的价值,往往收获颇丰.

强化训练(2007年高考湖南卷理科第20 题)已知双曲线x2-y2=2 的左、右焦点分别为F1,F2,过点F2的动直线与双曲线相交于A,B两点,(1)略;(2)在x轴上是否存在定点C,使-→CA·--→CB为常数? 若存在,求出点C的坐标;若不存在,请说明理由.[3]

将数据一般化,你能得到什么结论?

答案已知双曲线x2-y2=a2(a＞0)的左、右焦点分别为F1,F2,过点F2的动直线与双曲线相交于A,B两点,在x轴上存在定点使为常数.