一种基于PS-粗糙集的动态三支决策算法
2019-04-12张春英王立亚
张春英,乔 鹏,王立亚,秦 豪,刘 璐,唐 虎
(1.华北理工大学 理学院 河北 唐山 063210;2.河北省数据科学与应用重点实验室 河北 唐山 063210;3.华北理工大学 信息工程学院 河北 唐山 063210)
0 引言
三支决策理论是在传统二支决策只有两种决策规则(接受、拒绝)的基础上, 增加一种决策规则,即不承诺决策规则, 从而拓展为包括接受、拒绝和不承诺三个决策规则的理论模型[1-7].目前,三支决策理论已成功应用在多个领域中.文献 [8]通过对现有的三支决策理论和方法的分析,提出基于集对信息粒空间的三支决策模型;文献 [9]建立了基于集对联系熵的三支决策模型;文献 [10]提出了基于概率图的三支决策模型.这些模型的构建都是基于确定的集合,没有考虑到集合的动态变化.文献[11]提出了一种基于区间概念格的三支决策动态策略调控模型;文献 [12]提出了动态三支概率粗糙集的统一结构;文献 [13]针对延迟决策问题,以动态视角将基于概率粗糙集的三支决策推广到一个序列,提出了一种三支决策的动态决策模型;文献 [14]提出了一种面向决策对象变化的动态三支决策方法,设计了基于概率粗糙集模型的增量式三支决策算法,该算法可以有效利用原有信息系统中所获得的粒度结构和知识结果,从而实现概率粗糙三支近似地快速更新求解.而在实际问题中,往往会针对某信息系统U中的一部分子集X进行研究,而X也是动态变化的,既有新的对象从U中迁入到X中,也有X中对象迁出返回到U中.
文献[15-16]提出奇异集(简称S-粗集),为解决动态系统识别、动态系统决策、动态系统推理与动态证据合成等问题提供了有力的工具.而双向概率PS-粗糙集模型[17]既考虑集合的动态特性,又考虑知识库中的统计信息,提高了决策精度,是Pawlak粗糙集[18-19]和双向S-粗糙集的进一步发展.文献[20]首次提出将概率PS-粗糙集与三支决策相融合,构建了基于PS-粗糙集的动态三支决策的初步模型,根据双向概率PS-粗糙集的上、下近似重新划分了三支决策中的正域、负域和边界域,并基于不同区域给出了决策规则,但并未给出具体的算法.因此,在前期研究工作的基础上,本文进一步提出基于PS-粗糙集的动态三支决策算法,根据对象的迁入和迁出,讨论不同情况下的动态决策算法,并通过实验验证了算法的有效性和高效性.
1 概率PS-粗糙集上的三支决策模型
本节介绍PS-粗糙集的基本定义[17]与基于PS-粗糙集的动态三支决策模型的相关动态性质[20].
定义1设X*是X⊆U的双向S-集合,f∈F是定义在U上的元素迁移,给定一对阈值(α,β),且满足0≤β≤α≤1,则称F-(X*)(α,β)={x|x∈U,Pr(X*|[x]R)≥α}为X*依参数(α,β)的概率PS-下近似,称F-(X*)(α,β)={x|x∈U,Pr(X*|[x]R)>β}为X*依参数(α,β)的概率PS-上近似.称(F-(X*)(α,β),F-(X*)(α,β))为X*依参数(α,β)的概率PS-粗糙集.
根据概率PS-粗糙集模型可以得到一种新的正域、负域和边界域的划分.
定义2设X*是X⊆U的概率PS-粗糙集,X*⊆U,基于X*的概率PS的上、下近似,则X*的概率PS-粗糙集的正域、负域、边界域分别定义为
POS(α,β)(X*)=F-(X*)(α,β)={x|x∈U,Pr(X*|[x]R)≥α},
NEG(α,β)(X*)=U-F-(X*)(α,β)={x|x∈U,Pr(X*|[x]R)>β},
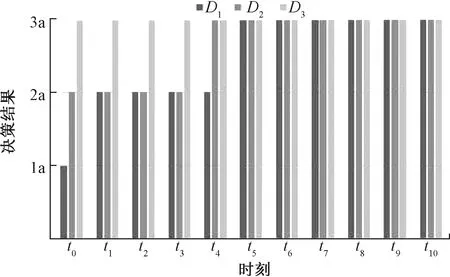
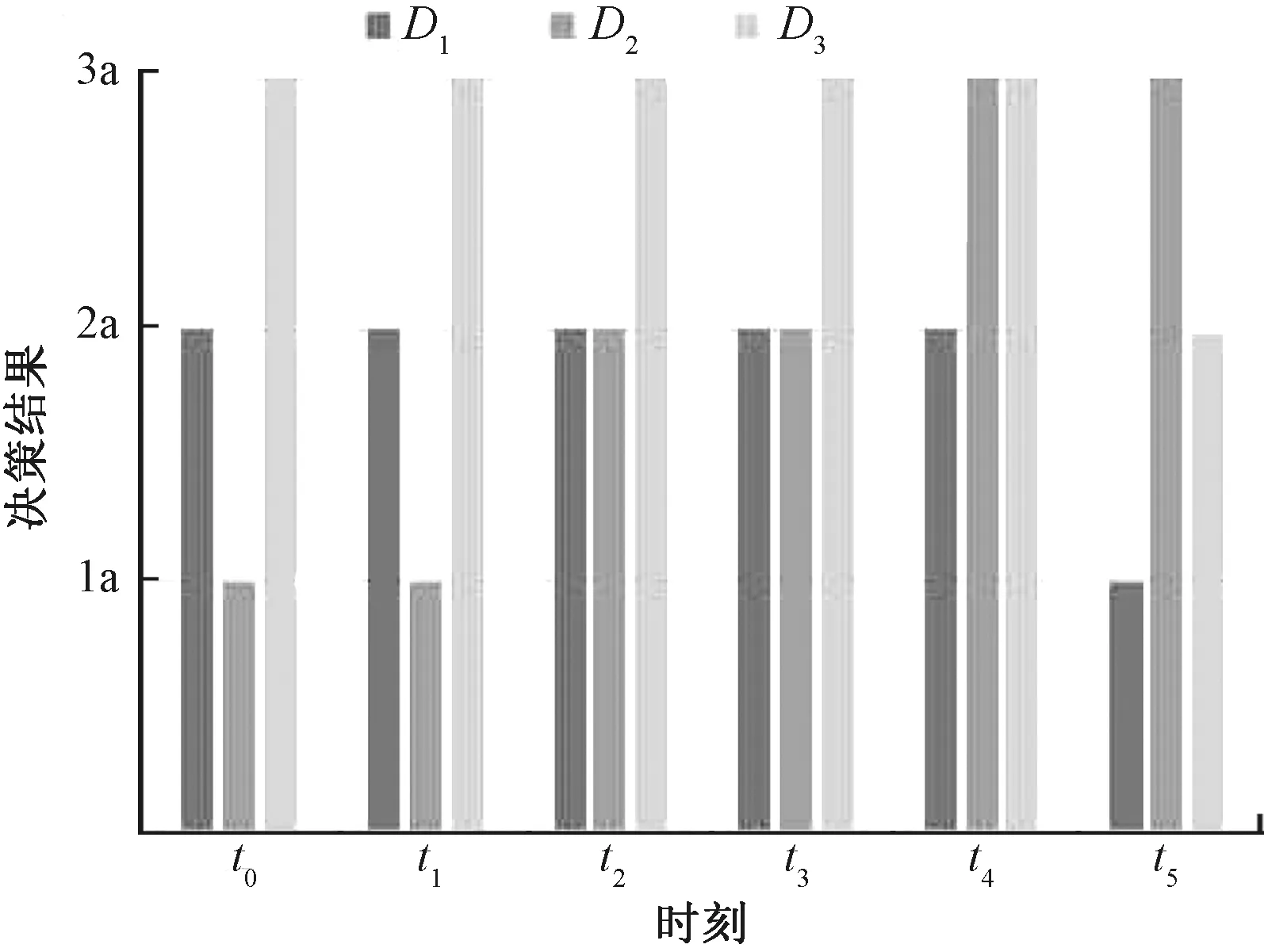
BND(α,β)(X*)=F-(X*)(α,β)-F-(X*)(α,β)={x|x∈U,β 设双向S-集合X*依参数(α,β)的概率PS-粗糙集的正域、负域、边界域分别为POS(α,β)(X*)、NEG(α,β)(X*)、BND(α,β)(X*),则有 正规则:Des(x)→接收,x∈X*,[x]R⊆POS(α,β)(X*), 负规则:Des(x)→拒绝,x∈X*,[x]R⊆NEG(α,β)(X*), 边界规则:Des(x)→既不接收也不拒绝,x∈X*,[x]R⊆BND(α,β)(X*). 在实际生活中,需要进行决策的对象往往是动态变化的,随时有新的对象迁入或迁出.动态三支决策的基本思想为:在给定决策信息数据集的条件下,可以根据决策属性进行决策分类,通过给出的确定子集和概率阈值,可以分别计算出条件概率,并与概率阈值进行比较,从而判断出对象属于正域、负域和边界域,根据概率PS-粗糙集上的三支规则做出接受、拒绝和既不接受也不拒绝的决策. 约定:S=(U,A,d)是一个决策信息数据集,其中U={x1,x2,…,xn}是所有对象的集合,A={a1,a2,…,am}是条件属性集合,{d}是决策属性.Xq是tq时刻的对象子集,设初始时刻为t0,子集为X0,按照决策属性划分的等价类为D1,D2,…,Dm,概率阈值为(α,β),每个等价类对应的条件概率分别为p1,p2,…,pm.下面分两种情况讨论动态三支决策的思想. (1) 仅有对象单向迁入或单向迁出子集 设ti时刻,或者有新对象加入到子集中,或者子集不变,或者有对象迁出子集,则每个时刻t1,t2,…,tn所对应的子集分别为X1,X2,…,Xn,迁入时子集之间的关系为X1⊆X2⊆…⊆Xn,迁出时子集之间的关系为X1⊇X2⊇…⊇Xn.设在ti时刻相对于Dj增加或减少的对象集为Δxj,i,且Δxj,i⊆Dj,则变化的对象集的条件概率表示为Pr(Δxj,i|Dj).由定理1和定理2知, 命题1设ti时刻新迁入或迁出的对象为x,x∉Dj,则对Dj中对象所做决策与ti-1时刻相同. 命题2设ti时刻新迁入的对象为x,x∈Dj,且迁入新对象后,有Xi∩Dj=Dj,那么对Dj中对象所做决策为接受;设ti时刻迁出的对象为x,x∈Dj,有Xi∩Dj=∅,那么对Dj中对象所做决策为拒绝. 命题3设ti时刻新迁入或迁出的对象为x,x∈Dj,迁入时,Xi∩Dj≠Dj,有X0∩Dj⊆Xi∩Dj,当Dj中对象在t0时刻所做决策为接受时,那么在ti时刻所做决策也为接受.迁出时,Xi∩Dj≠∅,有Xi∩Dj⊆X0∩Dj,当Dj中对象在t0时刻所做决策为拒绝时,那么在ti时刻所做决策也为拒绝. 命题4设ti时刻新迁入或迁出的对象为x,x∈Dj,迁入时,Xi∩Dj≠Dj,有X0∩Dj⊆Xi∩Dj,当Dj中对象在t0时刻所做决策为既不接受也不拒绝时,那么在ti时刻所做决策为:当Δp≥α-pj时,决策为接受;当Δp<α-pj时,决策为既不接受也不拒绝.迁出时,Xi∩Dj≠∅,有Xi∩Dj⊆X0∩Dj,当Dj中对象在t0时刻所做决策为既不接受也不拒绝时,那么在ti时刻所做决策为:当Δp′≥pj-β时,决策为拒绝;当Δp′ 命题5设ti时刻新迁入或迁出的对象为x,x∈Dj,迁入时,Xi∩Dj≠Dj,有X0∩Dj⊆Xi∩Dj,当Dj中对象在t0时刻所做决策为拒绝时,那么在ti时刻所做决策为:当Δp≥α-pj时,决策为接受;当β-pj<Δp<α-pj时,决策为既不接受也不拒绝;当Δp≤β-pj时,决策为拒绝.迁出时,Xi∩Dj≠∅,有Xi∩Dj⊆Xi-1∩Dj,当Dj中对象在t0时刻所做决策为接受时,那么在ti时刻所做决策为:当Δp′≤pj-α时,决策为接受;当pj-α<Δp′ (2) 同时有对象迁入/迁出子集 设ti时刻同时有元素迁入和迁出,设子集为Xi,若Xi-1∩Xi≠∅,设Xi-1∩Xi=Y,Xi相当于在子集Y中迁入了新的对象,计算出Y的条件概率,可以用情况(1)中的方法对Xi中的对象进行决策;若Xi-1∩Xi=∅,此时Xi中的对象为新迁入的全部对象,需要重新计算条件概率,并由决策规则进行决策. 算法基于PS-粗糙集的动态三支决策算法. 输入: 数据集U,子集X,等价类Dj(j=1,2,…),不同时刻迁入对象子集It(t=1,2,…)/不同时刻迁出对象子集Ot(t=1,2,…); 输出: 不同时刻的决策D={Dj|Dj∈POSITIVE}(j=1,2,…)或D={Dj|Dj∈BOUNDARY}(j=1,2,…)或D={Dj|Dj∈NEGATIVE}(j=1,2,…). Step1计算初始时刻X在每个等价类Dj下的条件概率pj,由决策规则做出初始时刻的决策. Step2当迁入新对象集It(t=1,2,…)时,判断新对象集It中的元素x是否属于Dj.若x∉Dj,则决策不变;若x∈Dj,判断Xi∩Dj是否等于Dj.若Xi∩Dj=Dj,则输出D={Dj|Dj∈POSITIVE},决策为接受.若Xi∩Dj≠Dj,初始时刻决策为接受,输出D={Dj|Dj∈POSITIVE},决策为接受.若Xi∩Dj≠Dj,初始时刻决策为既不接受也不拒绝,当Δp≥α-pj时,输出D={Dj|Dj∈POSITIVE},决策为接受;当Δp<α-pj时,输出D={Dj|Dj∈BOUNDARY},决策为既不接受也不拒绝.若Xi∩Dj≠Dj,初始时刻决策为拒绝,当Δp≥α-pj时,输出D={Dj|Dj∈POSITIVE},决策为接受;当β-pj<Δp<α-pj时,输出D={Dj|Dj∈BOUNDARY},决策为既不接受也不拒绝;当Δp≤β-pj时,输出D={Dj|Dj∈NEGATIVE},决策为拒绝. Step3当迁出对象集Ot(t=1,2,…)时,判断迁出对象集Ot中的元素x是否属于Dj.若x∉Dj,则决策不变;若x∈Dj,判断Xi∩Dj是否等于∅.若Xi∩Dj=∅,则输出D={Dj|Dj∈NEGATIVE},决策为拒绝.若Xi∩Dj≠∅,初始时刻决策为拒绝,输出D={Dj|Dj∈NEGATIVE},决策为拒绝.若Xi∩Dj≠∅,初始时刻为既不接受也不拒绝,当Δp′≥pj-β时,输出D={Dj|Dj∈NEGATIVE},决策为拒绝;当Δp′ Step4当有对象集迁入和迁出时,判断Xi-1∩Xi是否等于∅.若Xi-1∩Xi=∅,则计算Xi的条件概率,根据规则决策;若Xi-1∩Xi≠∅,记Xi-1∩Xi=Y,把Y当作初始时刻的子集,计算条件概率,Xi为Y迁入元素后的子集,按照迁入时的情况判断即可. Step5迁入/迁出对象子集是否为空,如果不为空,转到Step 2,否则结束. 选取了一组UCI数据集中用于活动识别的数据集作为实验数据,共有50 000个对象作为信息系统U,该数据集有三个条件属性和一个决策属性,根据决策属性将对象集分为三个等价类,分别为D1(由第1~20 000个对象组成)、D2(由第20 001~40 000个对象组成)和D3(由第40 001~50 000个对象组成).随机选取14 000、25 000和22 000个对象作为子集进行对象单向迁入、单向迁出和双向迁入/迁出实验.该实验在处理器为X64、RAM为4 GB的WIN10系统环境下用Java实现,通过选取子集Xi,对在Xi下三个等价类中的对象如何决策进行分析,并通过不断迁入/迁出对象到Xi,分析不同时刻等价类中对象的决策规律,决策结果中的1a、2a和3a分别表示拒绝、不承诺和接受决策. 随机选取14 000个对象作为实验子集X1,由1~4 000、20 001~25 000、40 001~45 000个对象构成,t1~t10时刻分别迁入新的子集,其中t1时刻的迁入子集I1={10 001~11 000,25 001~26 000,45 001~45 500},t2时刻的迁入子集I2={11 001~13 000,26 001~27 000,45 501~46 000},…,t10时刻的迁入子集I10={18 001~20 000}.设定概率阈值为(0.5,0.2),单向迁入实验结果如图1所示. 经过分析可知,t0时刻,由于子集中相对D1的对象个数较少,可以看出,D1、D2和D3分别属于负域、边界域和正域,根据决策规则,对三个等价类中的对象分别执行拒绝、既不接受也不拒绝和接受决策;在之后的每一个时刻,当有元素不断迁入到子集时,D3的决策在每一个时刻都为接受;t1时刻,有新的对象迁入到子集X1中,因为迁入对象属于D1等价类的相对较多,导致条件概率增加,对D1中对象做出的决策由拒绝变为既不接受也不拒绝,而子集对象相对D2的条件变化较小,因此决策不变;t2和t3时刻,虽然有新的对象迁入,条件概率相对增加但变化量不大,因此决策没有发生变化;t4时刻,D2的条件概率大于等于0.5,因此决策由不承诺变为接受;t5时刻,每个等价类的条件概率都满足决策为接受时的条件,因此对每个对象都做出接受决策.由结果可以看出,从t5时刻开始,三个等价类决策都为接受,当子集中不断地迁入新的对象时,决策都不会发生变化. 选取25 000个对象作为实验子集X2,由1~15 000、20 001~34 000、40 001~46 000个对象构成,t1~t10时刻分别从子集中迁出对象,其中t1时刻的迁出子集O1={1~1 000,20 001~21 000,40 001~41 000},t2时刻的迁出子集O2={1 001~2 000,21 001~23 000,41 001~42 000},…,t10时刻的迁出子集O10={14 001~15 000,33 001~34 000}.设定概率阈值为(0.7,0.3),单向迁出实验结果如图2所示. 图1 单向迁入实验结果Fig.1 The experiment result of one-way moving in 图2 单向迁出实验结果Fig.2 The experiment result of one-way moving out t0时刻,子集中属于D1和D2的对象相对较多,根据决策规则做出接受决策,而属于D3的对象相对较少,由概率阈值判断出D3属于边界域,因此做出既不接受也不拒绝决策;t1时刻,有对象从子集中迁出,概率阈值均减小,因为D2的条件概率减少得相对较多,所属区域变为边界域,因此决策需要进一步观察,而其他等价类的条件概率变化较小,决策不变;t2时刻,D1的条件概率减少到低于0.7,决策发生变化,此时三个等价类的决策都为不承诺;t3时刻,D3的条件概率减少,属于负域,因此,对D3的对象做出拒绝决策,在之后的每一个时刻,D3的条件概率都在下降或不变,而决策也不再变化,均为拒绝;t4和t5时刻,迁出对象后导致D1和D2的条件概率减少较多,因此对D1和D2做出不承诺决策;t6时刻,D2条件概率减少较多,变化较大,此时对D2做出拒绝决策;t7时刻,有对象的迁出,D1的条件概率减少到低于0.3,决策变为拒绝;t7时刻之后,D1、D2和D3均属于负域,对所有对象做出拒绝决策. 图3 双向迁入/迁出实验结果Fig.3 The experiment result of two-way moving in/out 选取22 000个对象作为实验子集X3,由1~10 000、20 001~25 000、40 01~47 000个对象构成,t1~t5时刻分别从子集中迁入/迁出对象.设定概率阈值为(0.6,0.3),双向迁入/迁出实验结果如图3所示. t0时刻,根据概率阈值及相应的决策规则可知,对D1中对象做出的决策为既不接受也不拒绝,对D2中对象做出的决策为拒绝,对D3中对象做出的决策为接受;t1时刻,相对于每个等价类的条件概率变化幅度较小,因此决策没有变化;t2和t3时刻,迁入了相对较多的D2中的对象,其他等价类下迁入和迁出的较少,因此只有D2的决策发生变化,由拒绝变为既不接受也不拒绝;t4时刻,子集中属于D3的对象没有变化,决策也没有变化,相对D2迁入了大量新的对象,只有少量的迁出,由此导致条件概率改变较大,做出的决策变为接受;t5时刻,子集中相对D1和D3迁出的对象多于迁入的对象,因此两个等价类下的决策均发生改变,而D2的条件概率变化值较小,决策没有变化. 三组数据子集以及迁入和迁出的对象集都是随机选取的,从图1~3中可以看出,算法给出的实验结果能清晰地判断决策类型,子集的不同、对象的迁入/迁出和概率阈值的设定都会影响决策结果的变化,同时也会影响决策的准确性.在后续的研究中,将继续讨论阈值设定对子集变化的影响. 本文提出了一个基于概率PS-粗糙集的三支决策动态算法,根据对象的迁入和迁出,讨论不同情况下的动态决策算法,进行了对象的单向迁入、单向迁出和双向迁入/迁出实验,通过实验验证了算法的有效性和高效性.该动态算法还涉及很多的问题有待进一步研究,例如概率阈值的优化、边界域对象的最优化处理方案和在具体决策中的应用等.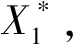
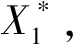
2 PS-粗糙集上的动态三支决策算法
2.1 动态三支决策的基本思想

2.2 算法描述
3 实验分析
3.1 实验环境
3.2 对象单向迁入实验与分析
3.3 对象单向迁出实验与分析

3.4 对象双向迁入/迁出实验与分析
4 结束语
