混沌理论和蝴蝶效应

张泽玲

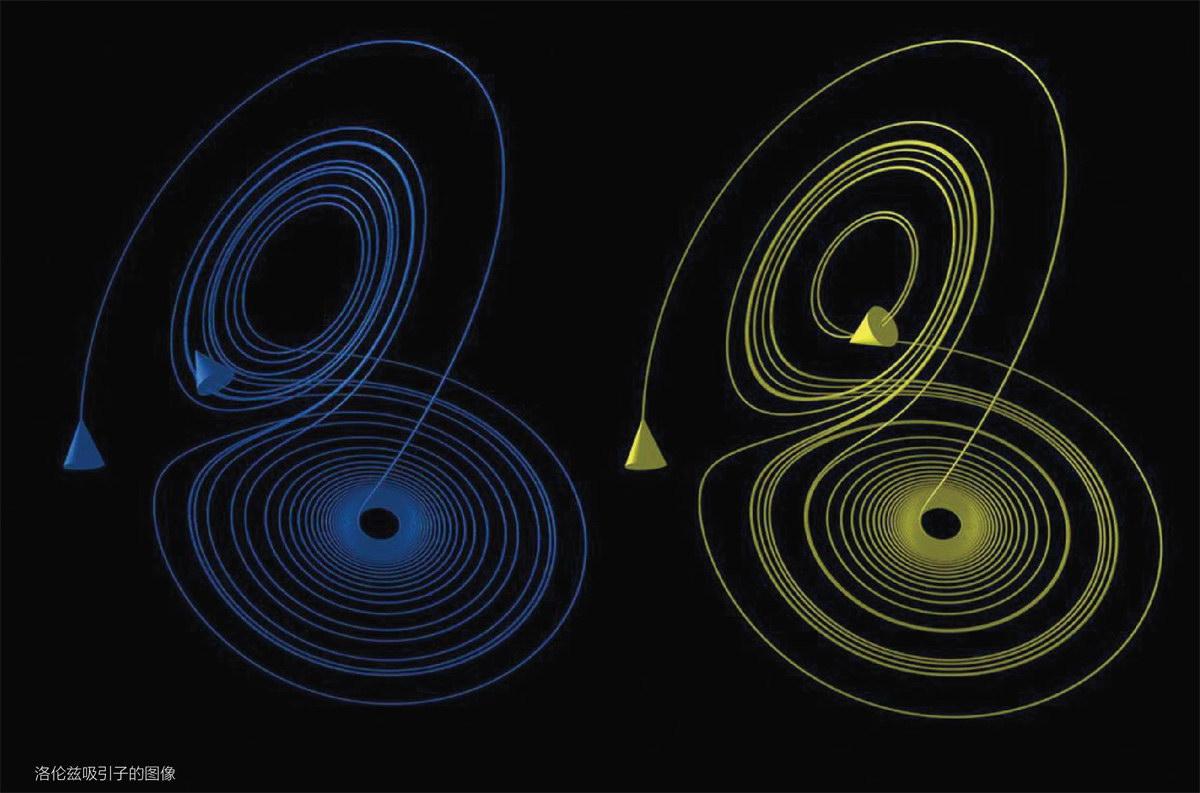
1961年冬天，气象学家爱德华·洛伦兹正在计算他所设计来模拟大气中空气流动的数学模型，可是他遇到了困难：不管怎样对数学模型进行修正，只要起始数据有一点点微小的差距，都会造成模拟结果的巨大差异。这种变化莫测的不确定性就被洛倫兹称为蝴蝶效应：巴西的蝴蝶扇一扇翅膀，可能会引起美国的一场龙卷风。巧合的是，在洛伦兹的这项工作中，计算大气方程中的对流方程时简化得到了一个方程轨迹的外形也像一只蝴蝶，这组方程的轨迹被称为“洛伦兹吸引子”。

具有“蝴蝶效应”这类现象的系统称为动力系统，研究动力系统行为的理论就称为混沌理论。混沌理论中运用了大量的数学工具，包括微分方程、拓扑学、微分几何、分形几何等。物理学中最难的分支之一——流体力学，就大量运用了混沌理论和偏微分方程来计算流体中的湍流。

混沌理论中还有一个更著名的例子：三体问题。混沌理论的起源，就是法国数学家庞加莱在研究三体问题时奠定了一系列理论。与《三体》小说中不一样的是，真实世界里的三体问题并不是完全不可解，只是从数学上证明没有唯一稳定解。历史上，数学和物理学家们算出了3组解。2013年，塞尔维亚物理学家米洛万·舒瓦科夫和迪米特拉·什诺维奇借助电脑，发现了新的13组特殊稳定解。

三体问题

就是指三个质量、初始位置和初始速度都是任意的可视为质点的天体，在相互之间万有引力的作用下的运动规律问题。