一类欧拉积分公式的计算方法及应用
2019-04-11邢家省杨义川王拥军
邢家省,杨义川,王拥军
(1.北京航空航天大学数学与系统科学学院,北京100191;2.数学、信息与行为教育部重点实验室,北京100191)
欧拉积分公式是数学分析中的重要经典成果[1-6]。文献[1,3]利用对含参变量积分的求导方法,给出了欧拉公式的证明,但证明过程较为繁琐,不易于被人掌握;文献[6-7]指出利用复围道积分方法也可得到欧拉积分公式,但所需知识较多,也不利于该法在数学分析中传播。正是这些文献中对欧拉积分公式证明的复杂性,限制了其传播和应用。
为了简化欧拉积分公式的证明方法,本文采用复数的欧拉公式表示,从而实现了对欧拉积分公式的简短证明,其中涉及的过程非常简单,利于人们对欧拉积分公式的理解和掌握。有几类重要的广义积分在以往的文献中是分别给予解决的,且解决办法相当复杂[7-20],而本研究发现利用欧拉积分公式可对这几类广义积分给出统一的处理。研究还利用积分交换次序定理[8-15]的结论给出了一类广义积分的计算结果,且在导出结果的过程中完全是利用数学分析已有的理论方法。研究以理论方法统一的形式传播来达到数学分析学中应有的概括高度,并形成了一套一般性的处理方法。
1 一类Euler积分公式的简便证明方法
定理1[1-6]
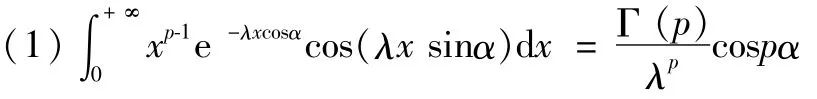

证明 记:
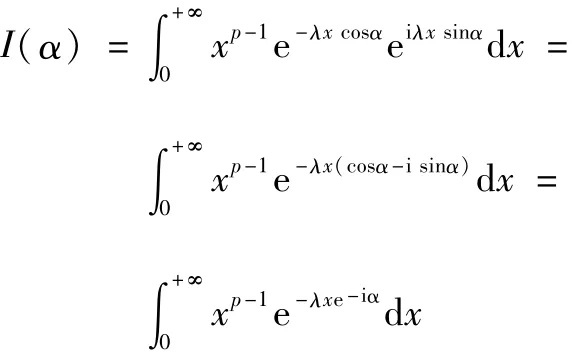

δ]是一致收敛的[1]。从而有:

于是I(α)=I(0)eipα,显然,两边分别取实部、虚部,就得定理1的结果。
文献[1,3]给出了定理1的证明,采用的是对实部和虚部分别求导的办法,证明过程较为繁琐。本文利用复数的欧拉公式表示,将其作为整体,采用对变量求导的办法给出了简短的证明过程,由此说明采用复数的欧拉公式表示可达到简化的结果。
此外,若取f(z)=zp-1e-λze-iα,在复平面上取特殊的围道,也可以给出用复积分的办法来计算定理1的结果[6-7]。对此不作详述。
定理2
式为:

证明
从而积分关于p在[0,1]上连续,且成立
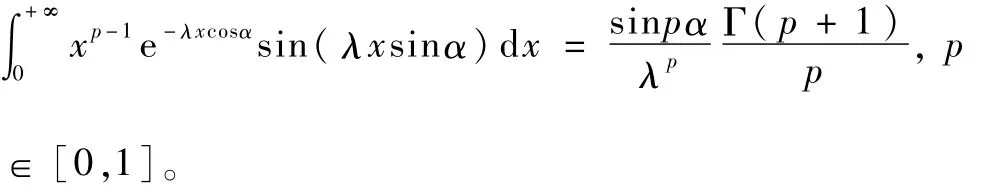
对-1<p<0,经过分部积分计算,并利用定理1的结果,可得:

定理2的结果得证。
定理3[1-2]

定理4[1-6]
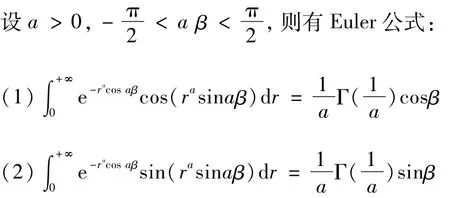
证明
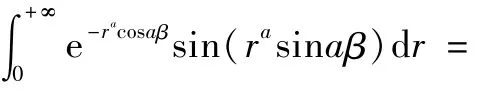
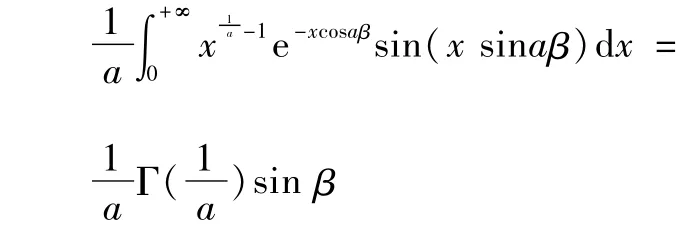
2 欧拉积分公式的直接应用
定理5[1-6]
设a,b>0,p>-1,则有:

证明

得到:

定理6[1-6]
设a,b>0,p>0,则有:

证明

得到:

记:


定理7[1-6]设a,b>0,p>0,则有:
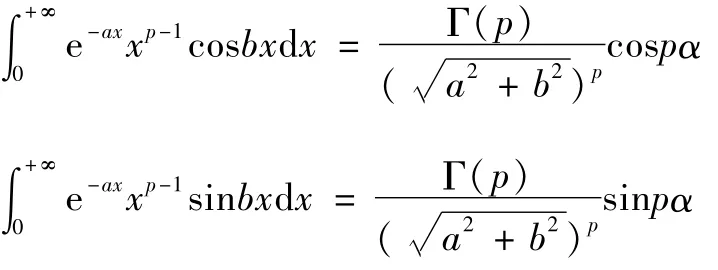
证明 记:

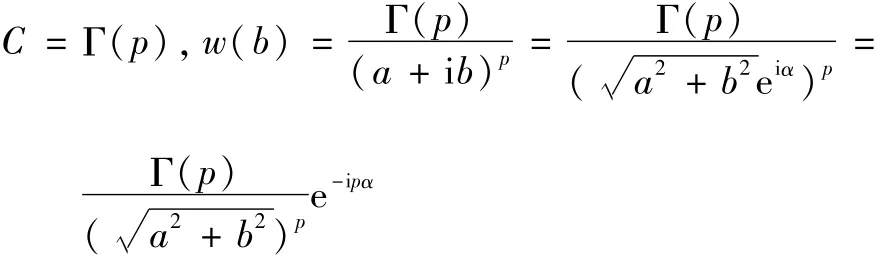
两端分别取实部和虚部,就可得到结果。
3 欧拉积分公式在广义菲涅尔积分计算中的应用
定理8[1-6]
设-1<p<1,则有:
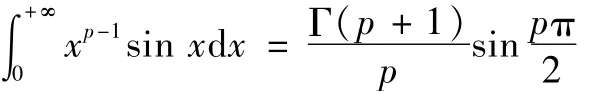
证明
定理9[1-6]
证明
4 欧拉积分公式在一些广义积分计算中的应用
定理10[1-6]
设k>0,-1<p<1,则有:

证明

利用积分交换次序的理论方法[8-15],可以证明有:

于是有:
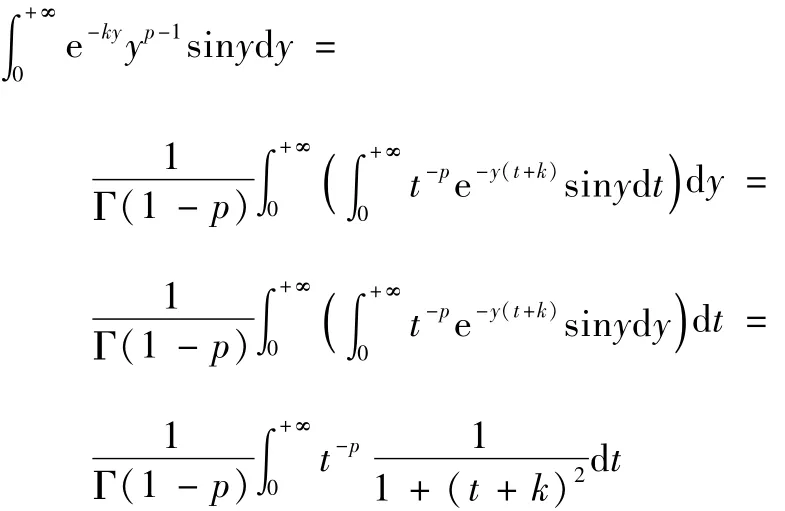
于是又有:
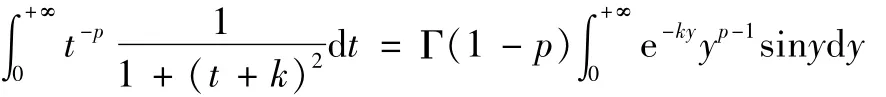
定理1的结果,得到:
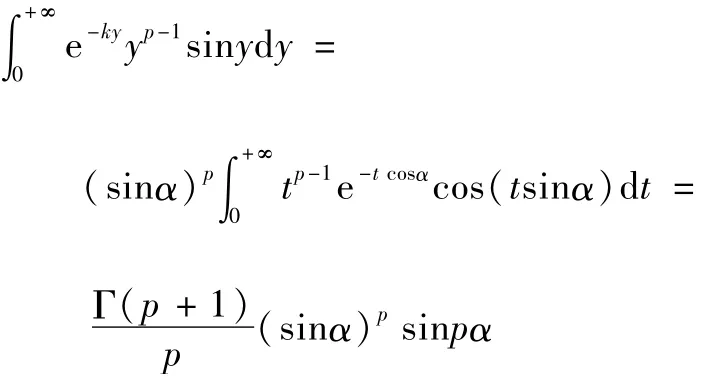

从而有:直接利用定理10的结果,可得下面定理11。
定理11[1-8]

定理12[1-8]
证明
对k>0,0<p<1,有:
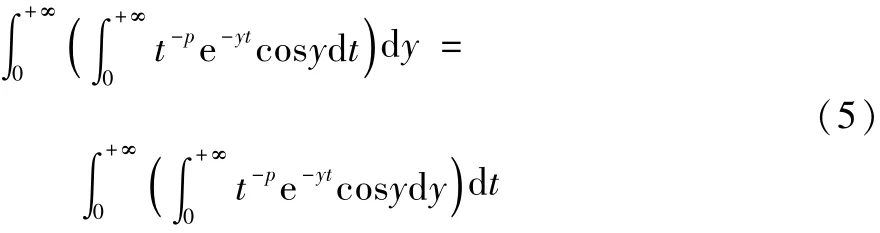
定理13[1-8]
设k>0,0<p<1,则有:
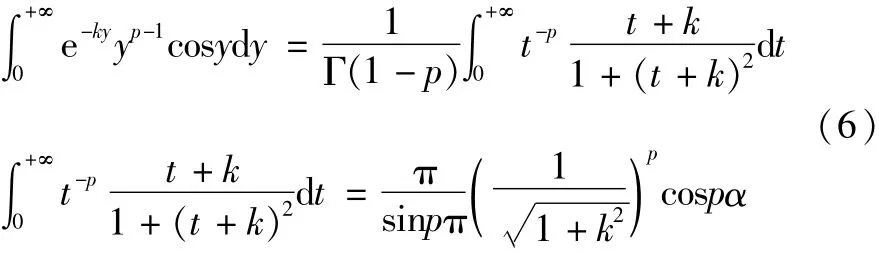
证明
),代入积分

利用(7)式,可得:

利用定理1的结果,得到:

于是:
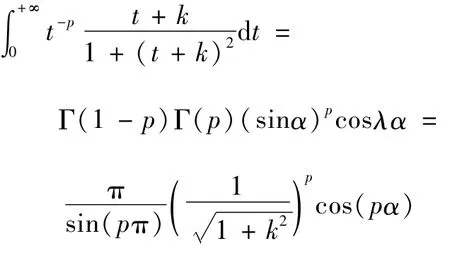
定理14[1-8]
设α≥0,则有:

证明
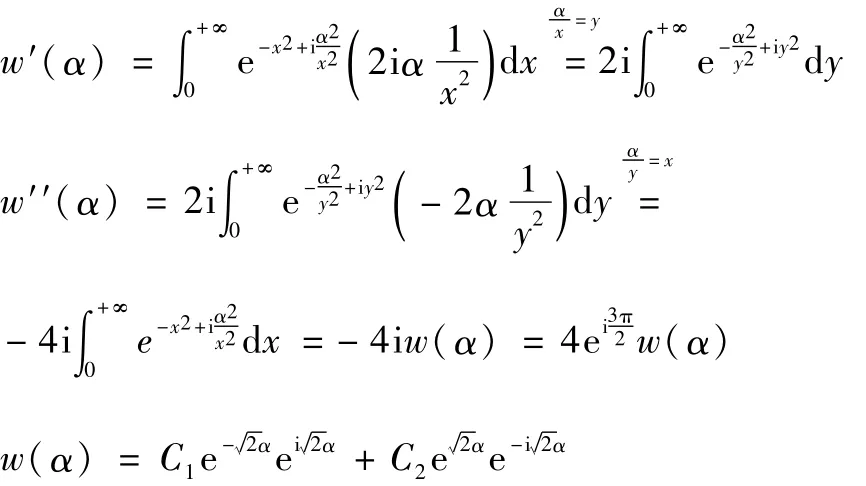
由于w(α)有界,所以

所以

于是有:

