考虑渗透力和Mohr－Coulomb准则时深埋球形洞室弹塑性解

2019-04-11谷新保蒋智明

四川轻化工大学学报(自然科学版) 2019年1期

黄华，谷新保，蒋智明

（四川轻化工大学土木工程学院，四川自贡643000）

引言

在隧道工程的稳定性研究中，圆形隧洞被很多人关注，是研究的重点，而球形洞室虽然也是一种受力合理的结构形式却较少受到关注，尤其是地下水对其的影响被忽略了。地下水是影响隧道稳定性的关键因素之一，尤其在围岩强度低、外水压力大的情况下，极易引起隧道围岩发生坍塌［1-2］。由于隧道开挖后形成的二次应力改变了原始地应力场分布及地下水渗流场分布，因此在研究饱和孔隙介质地层中隧道应力和位移分布时，必须要考虑渗透力的影响。

经典圆形隧洞是不需考虑渗透力的，但是对于水工隧洞来说，却是必须要考虑渗透力对其的影响。张黎明等［3］对虑渗透力下衬砌的圆形隧洞的弹塑性解进行了分析，把含水围岩简化为两相介质；黄阜等［4］利用原始的Hoek－Brown准则推导了地下水作用下圆形隧洞的解析解；文献［5－7］对渗流作用下井筒和巷道围岩的应力分布规律进行了研究。然而，这些研究都只针对圆形水工隧洞在地下水作用下的受力特征，却没有考虑球型隧洞的这种情况，更没有将两种不同形状受力进行对比分析。

鉴于此，本文在考虑渗透力的情况下，基于Mohr－Coulomb准则，推导出了球形洞室围岩应力与位移分布的解析解和塑性区半径，并将球形洞室与圆型洞室进行了对比分析，使球形隧洞的相关理论得到进一步发展，研究结果可为隧洞形状的选择和设计提供一定的理论指导。

1 模型假设

在深埋的岩体中开挖一球形洞室，其开挖半径为a，塑性区半径为ρ，弹性区半径为b＝βa，地应力为p0，渗流场静水压力为hf，开挖面支护力为p。计算模型如图1所示。

图1 计算模型

为了定性地研究渗透力对洞室围岩应力和位移分布的影响，做以下假设［8－10］：

（1）设渗流场静水压力沿径向均匀分布，在同一半径上大小相等，不考虑上覆土层自重应力；

（2）开挖支护力p沿开挖面径向均匀分布；

（3）围岩达到屈服后不会立即被破坏，而是保留一定的残余强度。

同时根据问题的特点采用球坐标，分别用r，θ，φ表示。边界条件为：σr／r＝a＝－p，σr／r＝βa＝－p0且忽略体力的影响；根据球对称可知：σθ＝σφ，εθ＝εφ；位移分量中仅有径向位移u，并且仅是r的函数，不随θ，φ变化，并以受拉为正。

2 渗流作用下球形洞室应力和位移场

2．1 渗流场

孔隙水压力η可由下式确定［11-12］：

式中：hf为渗流场静水压力。

地下水产生的径向渗透力Tr为［13-14］：

2．2 渗流场作用下球形洞室应力场弹性解

考虑渗透力作用下的平衡方程为：

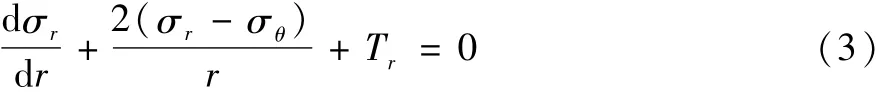
在球对称问题中，几何方程为：

式中，u为位移。

弹性本构方程为：

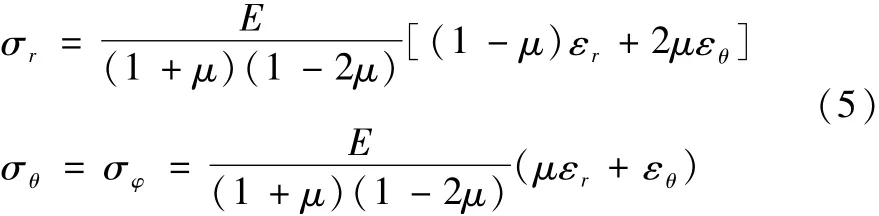
式中，E指材料的弹性模量。

联立式（3），式（4），式（5）得：

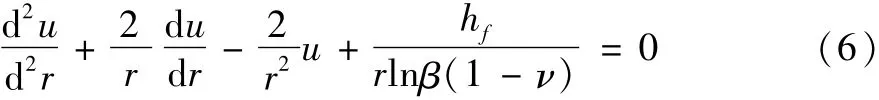
解方程得：

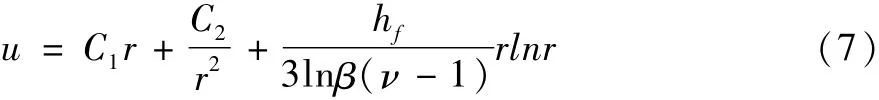
联立方程（5），（7）并带入边界条件σr／r＝a＝－p，σr／r＝βa＝－p0，得到弹性区的位移和应力场为［15］：式中为材料的泊松比。

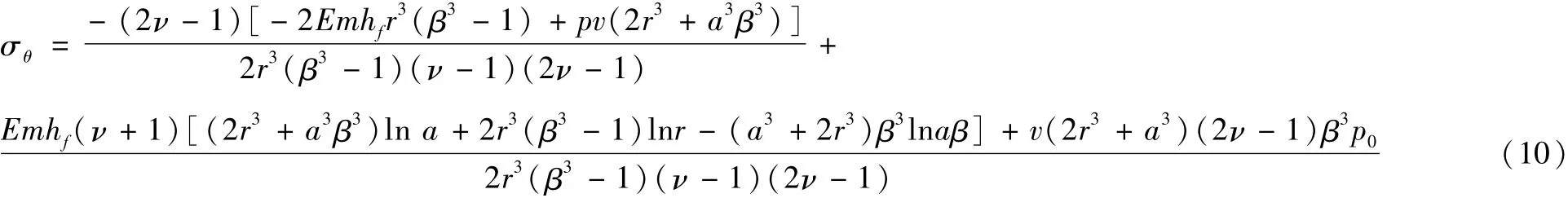
2．3 渗流场作用下球形洞室应力场和塑性区半径

开挖后，洞室周围产生应力重分布，当围岩应力场超出岩体的屈服应力时，将产生塑性区。假设塑性区应力符合Mohr－Coulomb屈服准则［16］，即：

式中，σ1，σ3分别为第一和第三主应力；c为粘聚力；φ为内摩擦角。当应力处于屈服的临界状态时有：

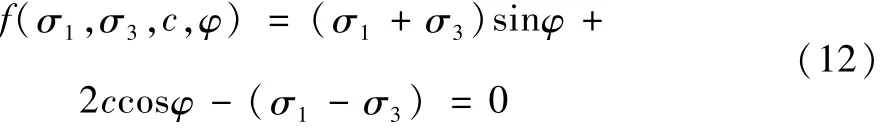
在球坐标下σr＝σ3，σθ＝σφ＝σ1，所以式（12）可以写成如下的形式：

把式（2），式（13）代入式（3）得微分方程：

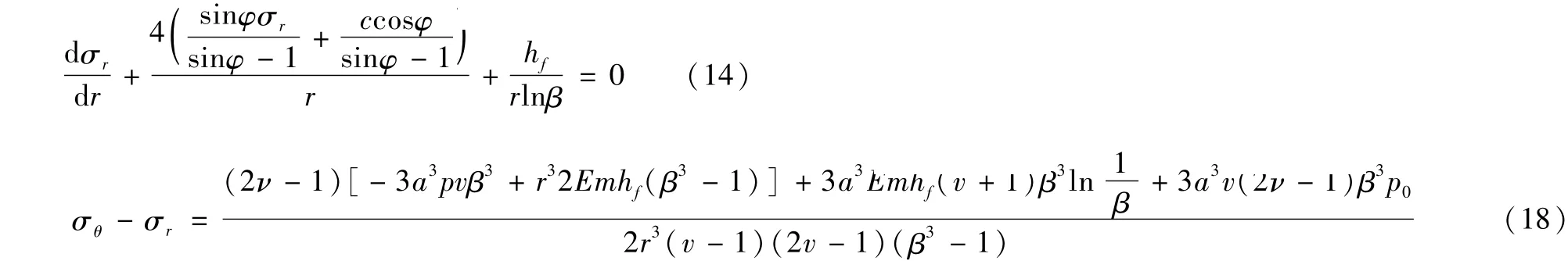
由式（14）可解得球形洞室塑性区围岩径向应力σr表达式为：

式中，A1为积分常数，由边界条件σr／r＝a＝－p确定，p为开挖面支护力。确定积分常数A1后，带入式（15）得到塑性区应力表达式：

将r＝ρ代入（15）得：

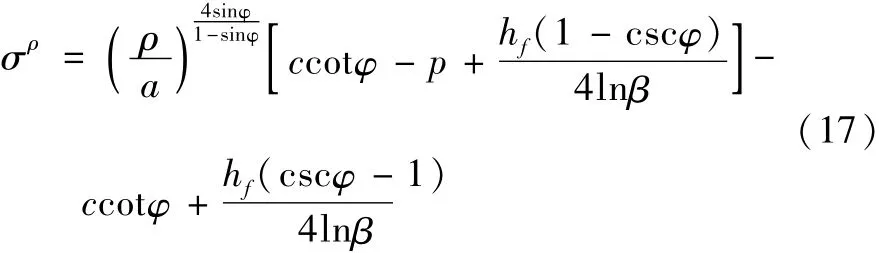
再由式（9）、式（10）得到：

由于弹性区和塑性区交界处的应力值相等，把r＝ρ和式（13）代入式（18），可得：

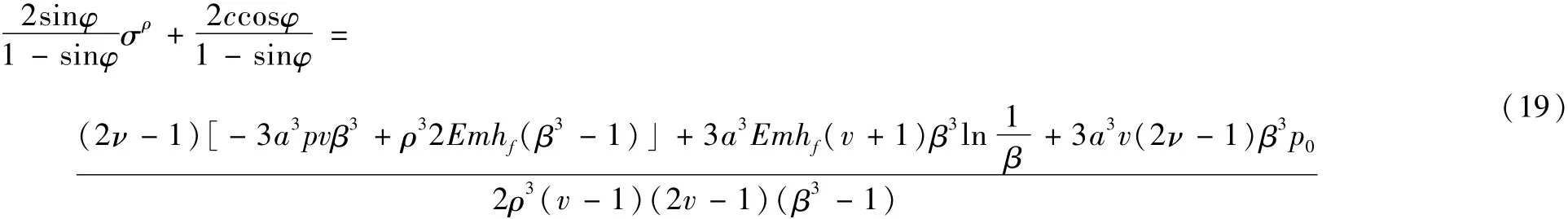
把式（17）代入（19）求得塑性半径ρ的计算公式为：

3 分析与讨论

3．1 渗流效应对围岩塑性区应力场的影响

取巷道半径a＝2 m，β＝20，E＝25×103MPa，φ＝30°，ν＝0.3，p0＝10 MPa，粘聚力c＝2.5 MPa，支护力p＝1 MPa。在不同渗透力下，考虑渗流力和不考虑时球形隧洞塑性区应力与半径的关系如图2所示。

从图2中可知，无论是否考虑渗流力，球形隧洞塑性区应力场都随其半径的增大而逐渐增大；当渗流力较小时，渗流效应对塑性区应力场的影响不大（图2（a）），但随着渗流力的增加，渗流效应对塑性区应力场的影响逐渐增加，考虑渗流力比不考虑时塑性区应力明显增大，且随着渗透力的增加径向和环向应力的增加幅度逐渐变大（图2（b）－图2（d）），因此当渗流力较大时必须考虑其对应力场的影响。

3．2 渗流效应对围岩塑性区半径的影响

取巷道半径a＝2 m，β＝20，E＝25×103MPa，φ＝30°，ν＝0.3，hf＝0.10 MPa，p0＝10 MPa，粘聚力c＝2.5 MPa，考虑渗流力和不考虑时球形隧洞塑性区半径随支护力的变化如图3所示。

图3 考虑渗流力和不考虑时球形隧洞塑性区半径随支护力的变化

从图3可知，对球形隧洞而言，当渗透力较时，在不考虑渗透力的情况下，随着支撑力的增大，塑性区半径先是缓慢增加，然后急速增加，到达某一最大值后，支撑力的继续增加对其不再产生影响；而在考虑渗透力的情况下，起初支撑力的增加对塑性区半径不产生影响，当其增加到某一值时，塑性区半径发生突变，达到最大，之后随着支撑力的增加，塑性区半径逐渐减少，至到平稳。由此说明，在考虑渗透力的情况下，支撑力的变化对塑性区半径变化产生了很大的影响，因此在富含地下水的地区开挖隧洞进行支护时必须考虑地下水的渗流效应。

3．3 渗流作用下不同洞室形状对围岩塑性区半径的影响

取巷道半径a＝2 m，β＝20，E＝25×103MPa，φ＝30°，ν＝0.3，hf＝0.10 MPa，p0＝10 MPa，粘聚力c＝2.5 MPa，r＝8 m。渗流力作用下不同洞室形状的塑性区半径与支护力关系如图4所示。

图4 渗流力作用下不同洞室形状的塑性区半径与支护力关系

从图4可知，在渗流作用下，圆形隧洞与球形隧洞的塑性区半径都随着支护力增加而逐渐减小，当支护力达到某一值时，塑性区半径都趋于稳定；不同的是圆形洞室塑性区半径一开始就很小，之后的变化极其缓慢，而球形洞室的塑性区半径一开始就比较大，之后急剧减少，因此球形隧洞的减小幅度远大于圆形洞室；此外，当支护力小于4 MPa时，球形洞室支护力对塑性区半径不产生影响，因此在考虑渗透力影响的情况下，当其他各项参数相同时，从洞室围岩稳定性角度考虑，采用球形洞室更有利。而当支护力大于4 MPa时，球形洞室塑性区半径大于圆形洞室，因此采用圆形洞室更有利。