基于深度强化学习的交通信号配时优化研究

2019-04-11张可新

沈阳理工大学学报 2019年1期

文峰,张可新

(沈阳理工大学信息科学与工程学院,沈阳 110159)

在交通拥堵状况日益严峻的当下,交通信号配时技术能解决交通配时问题,并且使得交通流得到控制、道路拥堵情况得到缓解、车辆碰撞频率得到降低。前人的研究表明,现实中交通信号配时问题是分布式的、混合的、复杂的[1-5];交叉口的交通状态是无规律的、难以直接预测的[6-9]。与传统的控制方法相比,基于Q学习的方法在交通信号控制上表现出了更高的性能[10],如:分布式多智能体Q学习、协同Q学习[11]。然而,传统Q学习中Q值表建立和搜索、目标Q值被高估、无法学习长期经验等问题在交通配时上不断显现,导致疏通环境交通拥堵的效果有限。深度学习具有较强的感知能力,而深度强化学习(DQN)是一种既具有感知能力,又具有决策能力的算法[12-14],较直接在交通信号配时上应用深度学习更具有决策能力。DQN应用于交通配时技术上,可以通过学习当前交叉口周围的交通状态和交通环境变化,对复杂的交通情况进行配时疏导,并从学习输入输出对的过程中寻找最优信号规划。然而,交通配时技术上的DQN模型大多采取将路口图像化,并利用卷积网络做预测配时[15-16],加剧了状态获取及反馈评价的复杂度。综合上述,本文提出采用双深度置信网络的DQN策略来对交叉口信号配时,以减少状态获取及反馈评价的复杂度,提高信号配时的有效性;此外,为保证训练目标的平稳性,避免其训练陷入目标值与预测值的反馈循环中震荡发散[17-18],采用DOUBLE DQN方法训练该DQN策略模型。

1 环境分析及策略模型

1.1 交通相位模型

路网由道路和交叉口组成,交通流的走向由交通相位决定。交通相位是指在一个周期内,交叉口上某一个或几个方向的道路上交通流具有通行的权利及绿灯时间,而另外一些方向上的交通流禁止通行。本文针对三岔口和四岔口分别定义两个相位模型,图1所示为三岔口相位模型;图2所示为四岔口相位模型;每个相位包括左转、右转、直行、调头[19]。

图1 三岔口相位模型图

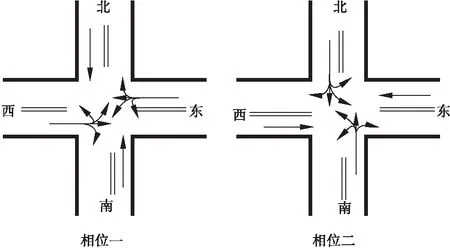
图2 四岔口交通相位模型图

1.2 DQN模型

DQN策略模型由四部分组成:预测网络、目标网络、环境和经验池。预测网络用来预测最优配时方案;目标网络用来辅助预测网络完成训练;环境是指交叉口周围的交通环境;经验池用来存储可供模型训练的样本数据。DQN策略模型的执行是由其四个组成部分不断交互完成,过程如图3所示。

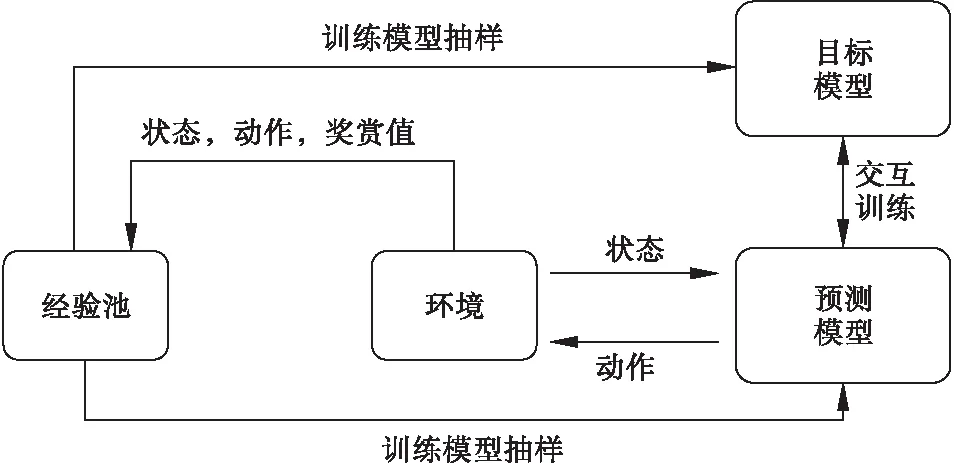
图3 DQN的基本模型

1.3 网络结构

为保证预测网络和目标网络交互的稳定性和准确性,两个网络采用同一深度网络结构。深度双网络结构如图4所示。

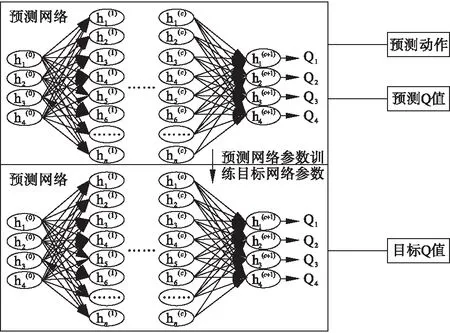
图4 深度双网络结构图

图4中:h为神经元;c为隐藏层;n为神经元个数。

其中预测网络用来生成当前环境状态下要执行的预测动作及模型训练所需的预测Q值;目标网络用来生成模型训练所需的目标Q值。目标网络与预测网络结合的训练方法即DOUBLE DQN。

2 DQN在交通配时中的应用

2.1 状态获取

根据DQN模型对输入状态信息的需求,把状态信息进行离散,如表1所示。

表1 状态信息离散

除表1状态信息外,把交叉口的坐标信息也加入到模型的输入状态中。为使路网中所有交叉口的状态信息都能运用同一网络模型来预测动作,统一输入状态信息的最终长度为最大交叉口状态空间的长度,如果部分状态长度不足则用零补齐。状态定义会影响动作选择的好坏和交通灯的控制性能,根据交叉口各周围车道的车辆拥挤度进行描述,对于有n个入边车道交叉口,其状态描述为s(x,y,d1,d2,…,dn)[19],其中,x、y分别为交叉口的横坐标和纵坐标;di表示第i个入边车道的车辆密度离散值。图1三岔口的状态值为s(x,y,d1,d2,d3,0);图2四岔口的状态值为s(x,y,d1,d2,d3,d4)。

2.2 动作选择

从图3中可知,策略模型学习过程的开始阶段,经验池中没有样本为双网提供参数训练,所以本文利用随机初始化的参数去执行预测网络的预测任务,并以上述模型为基础,把DQN的过程分为两部分:预决策过程和网络预测过程。预决策过程即用随机选择动作的形式对实验交叉口进行配时,该过程的目的是在不影响交通环境运行的同时收集多样化的经验样本,使策略模型具有更好的泛化能力。网络预测过程即用网络模型预测的Q值对交通信号进行配时,在该过程中为避免面临探索-利用困境,引入贪婪策略,即以ε概率随机选择动作进行配时,以1-ε概率网络预测动作进行配时。ε在每一次执行后都会衰减一定的步长Dropstep。Dropstep计算见公式(1),ε值计算见公式(2)和(3)。

Dropstep=(εstart-εend)/totalstep

(1)

εstep =εstartstep=0

(2)

εstep =εstep-1-Dropstepstep=0

(3)

式中:εstart为ε的开始值,其值为1;εend为ε的最终值,其值为0.1;totalstep为学习总步数。

2.3 经验存储

在DQN策略模型中,因为预测网络训练需要大量样本,所以引入经验池技术;其主要思想是存储过去的经验数据,避免预测网络只学习最新接触到的样本。本研究中,按DQN策略模型的训练要求组合当前状态、动作、下一时刻状态、奖赏值为一个有序列表,并作为经验样本信息存储进经验池。经验池样本数据运用Mini-Batch抽样参与DQN策略模型的网络训练。

2.4 模型训练

本文的DQN策略模型由预测网络和目标网络共同作用的DOUBLE DQN方法进行的模型训练。令st为交叉口的当前状态,at为st下该交叉口采取的配时动作,rt为at作用于交叉口后获得的奖励值,st+1为交叉口的下一个状态,at+1为st+1下该交叉口采取的配时动作。双网络训练中目标网络的作用是根据经验样本的状态值st+1预测产生该状态下的未来最大回报累计值qmax(st+1,at+1),从而参与公式(4)来计算st下的目标Q值q(st,at)。但目标网络直接产生st+1下的未来最大回报累计值,会使预测网络高估动作的预测Q值,这种高估可能导致预测值超出最优值[17];因此,用DOUBLE DQN技术来避免发生在交通配时上,即目标网络不再是完全生成st+1下的未来最大回报累计值,而是采用预测网络根据st+1预测产生的最优动作amax(qy(st+1,at+1))来选择目标网络对应的qtargety,作为st+1下的最大未来回报累计值,并参与st状态下的目标Q值qtarget的计算,计算公式见(5)。最后根据预测网络的预测Q值qy和DOUBLE DQN方法生成的目标Q值qtarget得到误差值loss,并根据误差值用随机梯度下降法来更新模型参数,误差计算见公式(6)。

q(st,at)=rt+γqmax(st+1,at+1)

(4)

qtarget=rt+γqtargety(st+1,amax(qy(st+1,at+1)))

(5)

(6)

式中:γ为衰减系数,其值为0.9;n为样本总数;i为样本索引。

3 仿真结果

3.1 仿真环境说明

实验采用sumo仿真器来模拟路网的运行环境。为验证研究的有效性,对传统Q学习的交通灯控制策略和DQN的交通灯控制策略,在相同路网环境配置下分别进行仿真实验。仿真时间步与时间秒相对应,总仿真时间步设为15000[20]。仿真路网环境配置信息如表2所示。

表2 路网信息

3.2 仿真结果分析

路网的总仿真时间分为前、中、后三个阶段,每个阶段的出车数量分别为少、较多、多。仿真实验得到两组测评数据:交通系统中的车辆数量、交叉口车道上车辆的平均行驶时间[20-21]。在传统Q学习和DQN两种策略下分析得出的两组测评数据,比较二者在配时过程的稳定性和有效性。

3.2.1 两种策略下阶段配时过程的稳定性分析

在两种策略下,用箱线图比较分析三个阶段路网中车辆数量和交叉口车道上车辆平均行驶时间的稳定性[20]。

图5为路网中不同阶段车辆数量分布对比图,图6为路网中不同阶段车辆平均行驶时间分布对比图。

图5 车辆数量分布对比图

图6 车辆平均行驶时间分布对比图

从图5图6中可以看出,基于DQN的交通配时策略模型在仿真前期出车数量较少时,能够把车辆数量及车辆平均行驶时间平稳的控制在一个较小的范围中;中期出车数量变多后,车辆数量及车辆平均行驶时间变化比传统Q学习稍微稳定;后期模型经过多次训练更新,其稳定性较传统Q学习强。由以上仿真结果得知,应用DOUBLE DQN方法来训练的DQN策略比传统Q学习策略更好的保证了配时过程中训练目标的平稳性。

3.2.2 两种策略下配时过程的有效性分析

在路网运行期间,每100s实时统计路网中车辆数量及交叉口车道上车辆的平均行驶时间,分别用柱状图和折线图作比较分析。

图7为每100s路网中的车辆数量对比图。