卧式滚筒内二元颗粒喷雾的数值模拟与分析
2019-04-11范元钢李世伟王正宏李建良
杨 玲,范元钢,李世伟,王正宏,李建良
(1.南京理工大学 理学院, 南京 210094; 2.辽宁庆阳特种化工有限公司, 辽宁 庆阳 111002)
颗粒喷雾造粒技术在农业、食品、兵器等工农业生产中有着广泛的应用[1-2],以含铝RDX炸药的生产来说,颗粒粘合剂包覆效果的好坏直接影响爆炸效率。对于实际的造粒过程中,准确的、实时的了解和掌握其在空间分布情况,将有助于提高产值。
尽管三维数值模拟能有效地、准确地模拟出颗粒的运动,但由于本文所要解决的是大质量颗粒喷雾造粒问题,三维模拟工作量巨大,由文献[11]知,若采用三维离散元EDEM模拟软件,对于由微米级颗粒组成的50 kg质量模拟,10 min混合时间需要计算机模拟几小时,模拟效率低,对于300 kg质量的模拟时间更长,在此初步考虑用二维模拟代替三维模拟。而在卧式滚筒中,颗粒在运动体系中左右对称,因此将三维体系化到二维体系是可行的。基于以上两点对卧式滚筒的颗粒喷雾造粒采用二维数值模拟的方法。
在实际的喷雾造粒过程中,一方面,各种力的作用使得颗粒运动,另一方面滚筒内颗粒被喷入粘合剂。现在已有的模型多半是基于干颗粒或含液量一定的湿颗粒的数值模拟[3-4],增加粘合剂浓度使颗粒生长速率增加等[5],对连续加入粘合剂过程的喷雾造粒的喷雾效果的模拟还没有相关研究。以离散元的力学理论为基础[6],通过追踪单个颗粒的运动模拟颗粒体的运动,研究喷嘴高度、喷雾流量喷雾效果,使每个颗粒周围尽可能的包裹有粘合剂涂层的综合最优参数,对模拟得出的结论给予理论解释。
1 颗粒运动与喷雾效果评估
1.1 颗粒运动
在颗粒运动的过程中,以离散元(DEM)为基础,交替使用牛顿第二定律和接触处的力-位移法则。牛顿的第二定律用于确定由接触力和作用于其上的力引起的每个粒子的平移和旋转运动,而力-位移定律用于更新每个粒子相对运动产生的接触力。本文用线性接触模型、滑移模型、并行接触模型的组合来表示颗粒之间的力[7-9],具体过程如下。
线性接触模型的切向接触力是通过切向接触力增量来定义,两颗的法向接触力Fcn和切向接触力增量ΔFcs、切向接触力Fcs分别为
(1)
(2)
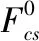
库伦滑移接触模型允许颗粒之间发生滑移,若切向接触力大于最大允许滑动接触力时,颗粒在下一步计算时发生滑移,即
Fcs=min|Fcs|,μ|Fcn|·signFcs
(3)
其中:μ为接触处的摩擦系数[10];sign(x)为符号函数。
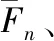
(4)
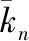
作用在并行约束外围的最大法向应力σmax和最大切向应力τmax计算为:
(5)
(6)
如果最大法向应力σmax超过法向约束强度σ或最大切向应力τmax超过切向约束强度τ时,并行约束断裂,此时平行接触模型从模型中移除,湿颗粒间接触或者颗粒间距离小于半径的10-6倍,形成平行接触模型[11]。
1.2 喷雾效果评估
喷雾效果的好坏用颗粒的质量平均增加量和受到喷雾的颗粒比例,即包裹合格率来评价,具体方法如下。
设数值模拟二元颗粒的质量为M,个数比为nA∶nB,质量为M的二元颗粒对应两种颗粒的个数分别为NA∶NB,则可得
(7)
即
(8)
注:若不作说明,则长度单位均为厘米,质量单位均为克,时间单位均为秒。
设喷雾流量为vl,喷雾时间为t,溶质均匀地包裹在颗粒表面,假设粘合剂均匀喷雾时每个颗粒的平均包裹量与颗粒的半径成正比,则
(9)
k为粘合剂均匀包裹在每个颗粒上时,每厘米粒径的质量增量。颗粒包裹量过小或过大包裹效果都不好,因此把颗粒的增量p分为6个标准,评判标准见表1。

表1 评判标准

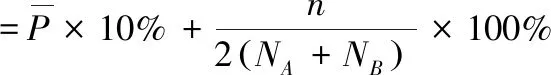
(10)
2 喷雾相关参数分析
2.1 喷嘴高度设置问题
首先推导喷嘴的高度。喷雾截面模拟图如图1,设滚筒的半径为R,滚筒长度为d,喷雾锥角为θ,设颗粒填充率为α时,滚筒截面圆心与颗粒表层的夹角为β,则
(11)
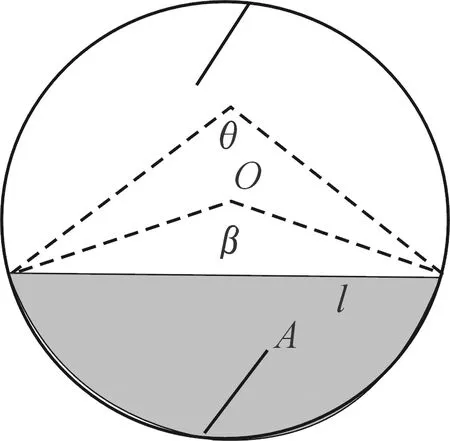
图1 喷雾截面模拟图
即
β-sinβ=2πα
(12)
为便于叙述,我们把式(12)写成
β=f(α)
(13)
即角β是关于填充率α的对应关系,则可得到滚筒内颗粒的表层长度l为
(14)
在喷雾时,喷洒面积越大,喷雾效果越好。当喷头的喷雾角为θ,粘合剂完全喷洒颗粒表层时,喷头距滚筒底部高度h为
(15)
在喷雾过程中,滚筒转动时喷嘴安装高度不能超过抄板板头A转动的区域。由式(15)知喷嘴的安装位置与颗粒的滚筒半径、填充量、喷雾锥角有关。
2.2 溶剂喷雾速度和模拟方法
喷雾过程中假定粘合剂完全包裹在颗粒表面时,溶剂恰好蒸发。假设实心锥喷嘴在喷雾区域喷雾均匀,二维模拟卧式滚筒内颗粒的喷雾轴向长度为l,因为二维模拟,所以结合由1.2节内容,数值模拟的时间t为
(16)
其中w为含液量。
设径向喷雾区长度为li,模拟中每0.2 s执行一次喷雾,更新一次径向喷雾区长度,并算出颗粒的增量。则二维模拟的颗粒进入喷雾区后喷雾长度随时间的分布为:
(17)
3 数值模拟与分析
3.1 喷嘴安装高度模拟分析
由2.1节可知,在喷嘴高度为h时理论上喷雾效果最好,为验证推导的正确性,在滚筒上加0.4R且与水平面夹角为60°的抄板,参数选取见文献[12-13],取颗粒质量分别为100 kg、200 kg、300 kg,填充率α为30%时,1个实心锥喷嘴,喷雾流量vl为40 g/s,喷雾锥角θ为90°。选喷嘴高度分别为h、h-0.1R、h-0.2R、h-0.3R这4组高度模拟颗粒喷雾合格率。具体模拟仿真所用的颗粒参数列于表2。为确保离散元数值模拟时颗粒接触检测的准确性和高效性,数值模拟仿真时选择时间步长为1.0×105s,每隔0.2 s执行一次喷雾,即计算一次颗粒质量增量,模拟的总时长由喷嘴高度等参数变化而变化。
模拟得到的喷雾合格率随喷嘴高度变化如表3所示。
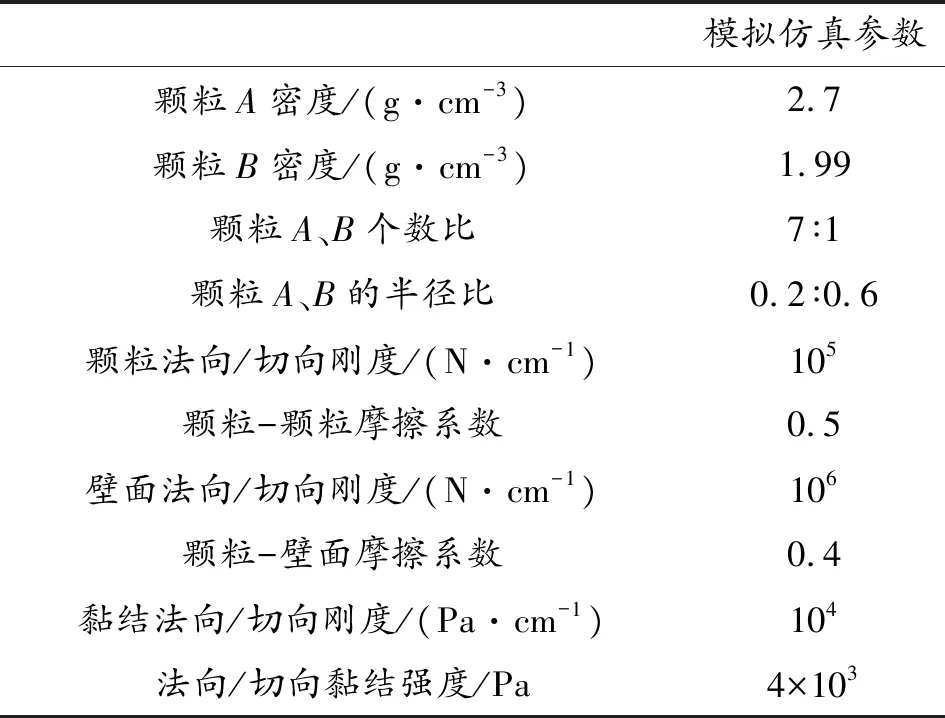
表2 模拟仿真参数
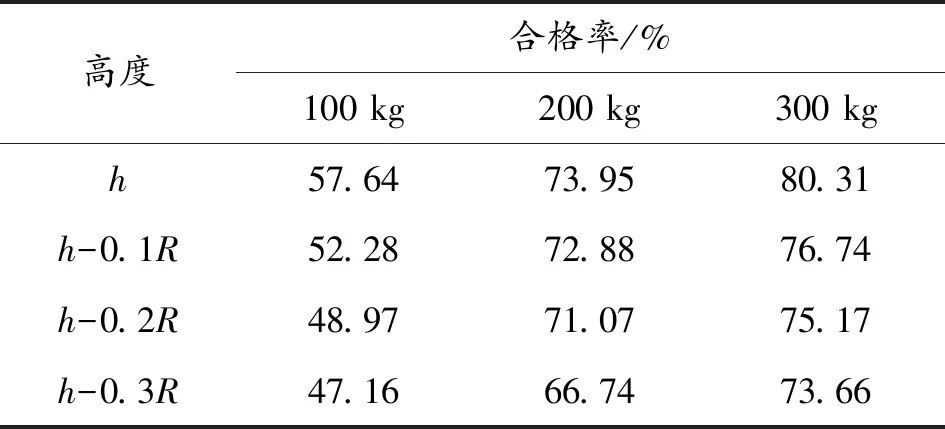
表3 喷嘴高度与合格率
合格率随喷嘴高度的变化如图2所示。
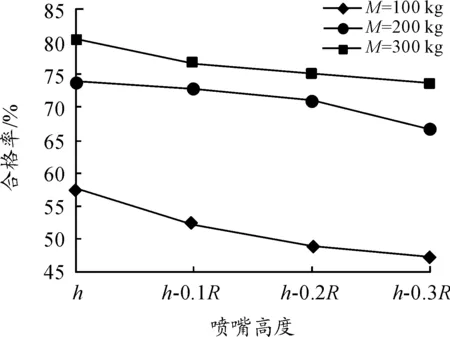
图2 合格率随喷嘴高度的变化
从表3的数据可知,在喷嘴高度为h时,喷雾效果最好。由图2可直观地看出,在其他条件相同时,随着颗粒质量的增加,喷雾合格率变大。
3.2 喷雾流量模拟分析
由3.1节可知喷嘴安装高度为h时喷雾效果最好。以喷嘴高度为h,研究喷雾流量对颗粒喷雾效果的影响,模拟参数如3.1节。模拟得出的喷雾合格率见表4。
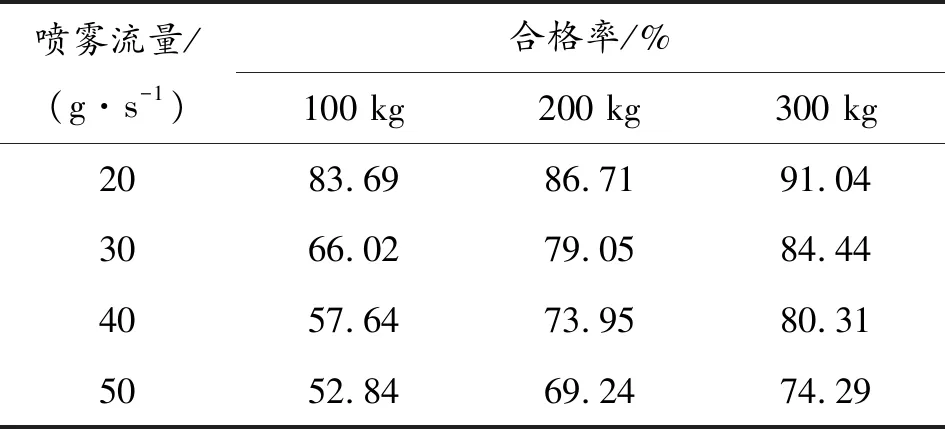
表4 喷雾流量与合格率数据
喷雾合格率随喷雾流量度的变化如图3所示。
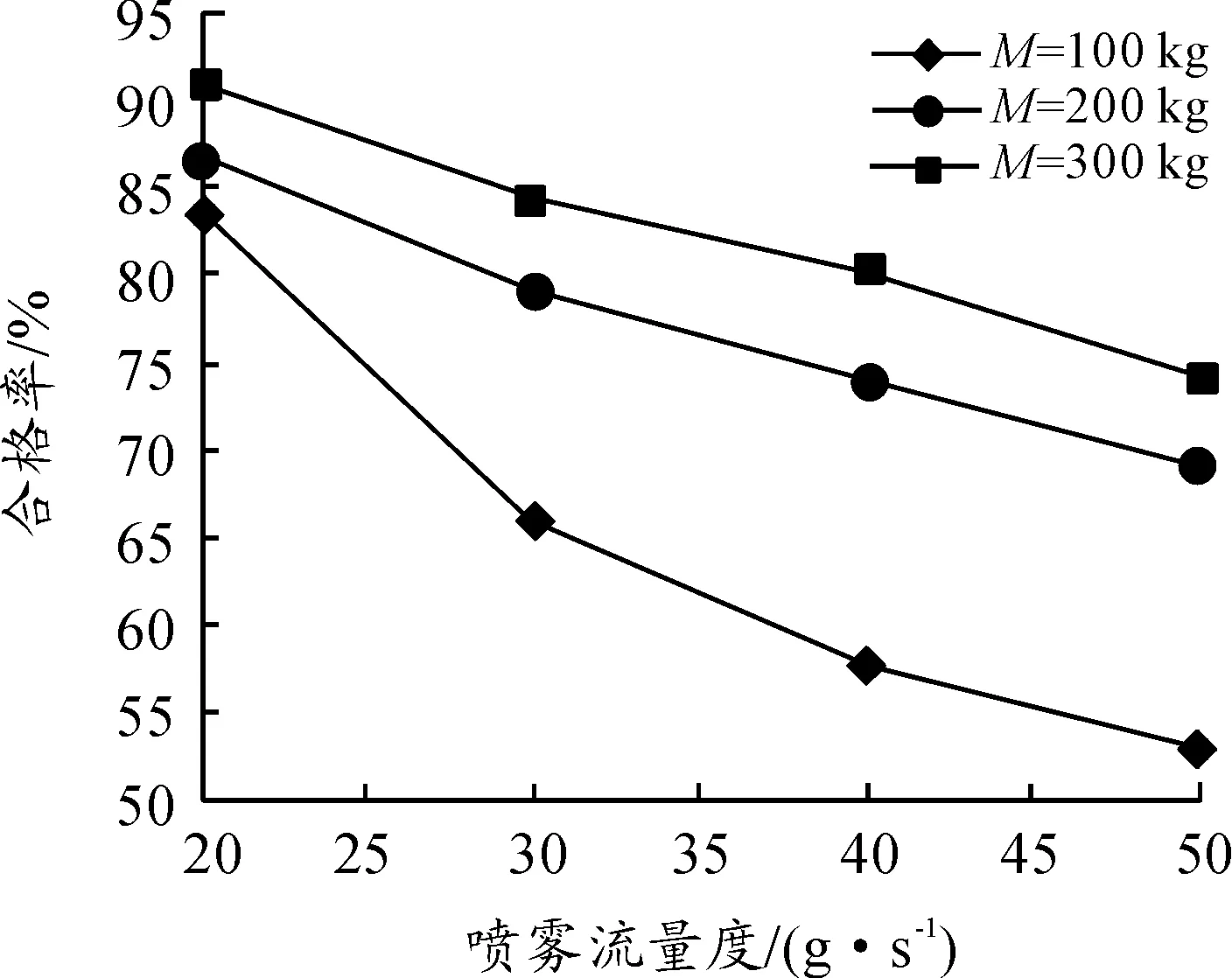
图3 喷雾合格率与喷雾流量度的变化
由图3可知随着喷雾流量的增大喷雾合格率减少,喷雾效果变差。喷雾流量较小时,喷雾合格率随颗粒质量的变化较小;当喷雾流速较大时,喷雾合格率随颗粒质量的变化较大。对比3.1节内容可知其他条件一定时,喷雾合格率随着颗粒质量的增加而增大。以颗粒质量为200 kg为例,不同的喷雾速度下喷雾合格率随时间的变化如图4所示。
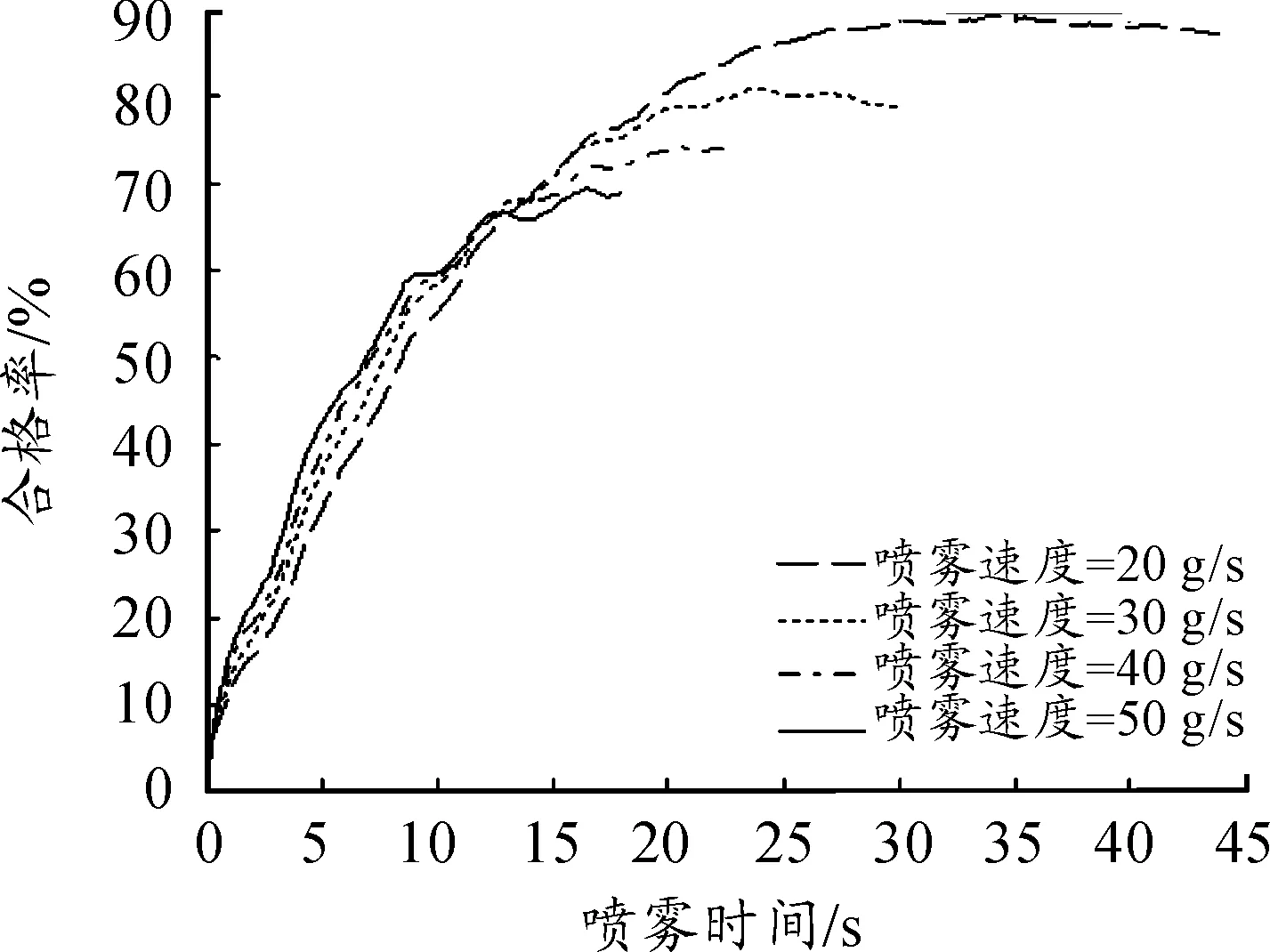
图4 喷雾合格率与喷雾时间的关系
由图4可知喷雾合格率在喷雾开始时迅速增加,在喷雾后期增加缓慢,且喷雾速度为20 g/s时,喷雾时间大于35 s,喷雾合格率稍稍下降;喷雾速度为30 g/s时,喷雾时间大于25 s,喷雾合格率也有下降的趋势。
4 结论
2) 虽然喷雾流量越小,喷雾效果越好,但喷雾完成所需要的总时间也越长,造粒效率变差,且喷雾流量较小时,喷雾后期喷雾合格率有变小的趋势。因此在生产中可适当增加喷雾流量提高生产率。100 kg质量的颗粒,喷嘴高度为h,喷雾流速为20 g/s时,喷雾合格率为83.69%;300 kg质量的颗粒,喷嘴高度为h,喷雾流速为30 g/s时,喷雾合格率为84.44%。因此100 kg到300 kg的颗粒达到84%的喷雾合格率时,喷雾流速提高,生产率提高。
