Accretive-dissipative矩阵的行列式不等式

薛建明

(昆明理工大学 津桥学院，云南 昆明 650106)

(1)

在 (1)式中，A11和A22分别是k和l阶的，并令m=min(k,l)。

2004年俄罗斯数学家Ikramov在文献[1]中证明了Accretive-dissipative矩阵的行列式不等式：若A∈Mn(C)是Accretive-dissipative矩阵且分块如 (1)，则

|detA|≤3m|detA11|·|detA22| 。

(2)

2013年Lin在文献[2]中得到了比 (2)式更好的结果：若A∈Mn(C)是Accretive-dissipative矩阵且分块如 (1)，则

(3)

最近几年，许多学者发表了关于Accretive-dissipative矩阵不等式的一些文章，详见文献[3-6]。在本文中，我们主要研究Accretive-dissipative矩阵的行列式不等式，并得到了比 (3)式更好的结果。

1 主要结果

为了得到主要结果，我们首先给出如下引理。

引理1[1]设A∈Mn(C)是Accretive-dissipative矩阵且分块如 (1)，则A-1=D-iE，其中D=(B+CB-1C)-1，E=(C+BC-1B)-1。

引理2[7]设B,C∈Mn(C)是Hermitian矩阵且B是正定的，则B+CB-1C≥2C。

引理3[2]设B,C∈Mn(C)是半正定矩阵，则|det(B+iC)|≤det(B+C)。

引理4 设A,B∈Mn(C)是正定矩阵，则

det(A+B)≤rn|det(A+iB)|，

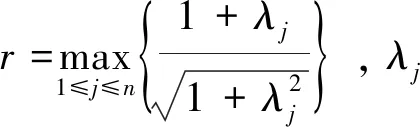
=rn|det(A+iB)|。

定理1 设A∈Mn(C)是Accretive-dissipative矩阵且分块如 (1)，则

|detA|≤2mrm|detA11|·|detA22|，

(4)

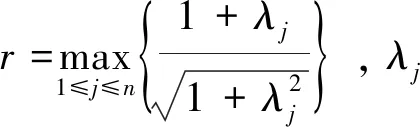
证明当m=l时，令

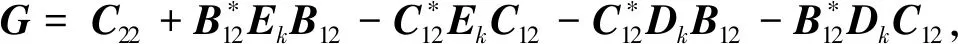
由引理1，引理2可知，

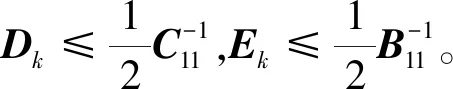
(5)

因为B,C是正定矩阵，所以

(6)

由(5)和(6)可知，

(7)

由引理3，(7)和引理4可得

|det(A/A11)|

= |det(F+iG)|

≤det(F+G)

≤det(2B22+2C22)

≤2mdet(B22+C22)

≤2mrm|det(B22+iC22)|

≤2mrm|detA22|。

当m=k时，类似可得

|det(A/A22)|=2mrm|detA11|。

由|detA|=|detAii|·|det(A/Aii)|(i=1,2)可得

|detA|≤2mrm|detA11|·|detA22|。