一个野代数的二维的不可分解表示
2019-04-10刘雨喆
刘雨喆,章 超
(贵州大学 数学与统计学院,贵州 贵阳 550025)
代数表示型问题是代数表示理论中的基本问题之一。所谓表示型问题,即研究有限维k-代数的不可分解模的分类问题。域k上的有限维代数自然地分为两类:表示有限的代数和表示无限的代数。这里,表示有(无)限代数是指模范畴中具有有(无)限多个不可分解对象。对于表示无限的代数,Donovan-Freislich猜想它们可以分为更细致的两类, 即驯(tame)表示型代数和野(wild)表示型代数[1]。 粗略地说,一个代数是驯表示型代数当且仅当它的不可分解表示可以由一个连续变量来量化,而野表示型代数具有由任意多变量量化的不可分解表示。后来Drozd利用矩阵方法证明了上述双分定理[2]。更细致地说,表示野代数的定义依赖于代数Γ=k〈x,y〉的表示范畴。通常来说,完全描述野代数的表示范畴是不可能的。代数Γ本身也是表示野代数。
由Gabriel图化理论,代数Γ同构于箭图Q=(Q0,Q1)对应的箭图代数kQ,其中点集Q0={1},箭向集Q1={α∶1→1;β∶1→1}。由文献[3]中表示理论可知,代数kQ的n维表示即为Y=(kn,A,B),其中A,B为n阶方阵。给定代数kQ的另外n维表示Y′=(kn,A′,B′),M≅M′当且仅当存在可逆矩阵P,使得P-1AP=A′,P-1BP=B′。因而计算该代数表示的同构类问题,等价于解线性矩阵问题:给定矩阵对(A,B),是否存在可逆矩阵P,使P-1AP,P-1BP同时为在某一确定意义下的标准形。对任意给定的矩阵对,Belitskii约化算法却是确定其相似标准形的一个有效算法[4-6]。Jordan标准形理论表明一定存在可逆矩阵P,使得P-1AP为Jordan形矩阵。Belitskii算法的基本思想是在保持J不变的情况下,继续约化M=P-1BP时,矩阵集合只能是Λ={S∈GLn(k)|SJ=JS},其中GLn(k)表示数域上的全体可逆n阶矩阵组成的一般线性群。Belitskii标准形的参数数,粗略地说,是代数群G={S∈Λ| det(S)≠0}作用在由这些矩阵M构成的代数簇上的一个量化参数,它的定义依赖于单个矩阵M在共轭作用下的G-轨道的维数与余维数[7]。本文中我们总假定k为代数闭域。本文主要计算代数Γ=k(x,y)所有二维表示的同构类,并利用Belitskii算法得到的标准形,计算了Belitskii标准形的参数数。
1 Belitskii约化算法
为了文章的完整性,本节将介绍约化矩阵对(A,B)的Belitskii算法,详见文献[4-6]。
令W为Jordan标准形或者Weyr标准形,Λ={X∈GLn(k)|XW=WX}。Λ由分块上三角阵X=(Xij)d×d组成,(Xij)d×d为与W相同分块的矩阵。
定义1.1设M,N是两个n阶方阵。如果存在矩阵P∈Λ,使得P-1MP=N,则称M是Λ-相似于N的,记作M~ΛN;我们称M的子块Mij是Λ-稳定的,如果对任意的X∈Λ,Mij在Λ-相似变换MaX-1MX下保持不变;对于分块矩阵M=(Mij)d×d,我们规定:Mi1j1 如果M所有的子块都是Λ-稳定的,那么M在相似变换MaX-1MX(X∈Λ)下保持不变,此时M本身就看作一种标准形。否则,设Mlr是M=(Mij)d×d的第一个在上面序下的非Λ-稳定子块。令X-1MX=M1,则MX=XM1的第l行第r列子块为 又由于所有满足Mij (1) 以下对可能存在的三种情形进行约化: 本节我们将应用上一节介绍的Belitskii约化算法计算二维表示的同构类,该结果将给出二阶矩阵对的相似分类。我们利用Belitskii标准形给出了参数数。 当矩阵对(A,B)中A,B均为二阶矩阵时,以矩阵B的Jordan矩阵标准形进行分类。 其中a11,a12,a22为参数。 则a22,a11,a12都Λ-稳定,所以 其中a11,a12,a22为参数。 其中a11,a22为参数。 其中a11,a12为参数。 则a11,a12都Λ-稳定,所以 其中a11,a12,a21为参数。 令(Ψ,Λ)为前面小节中的线性矩阵问题,其中Ψ为满足特定条件矩阵M构成的代数簇,代数群G={S∈Λ|det(S)≠0}共轭作用在这些矩阵M上,M的G-轨道ΟM即为M的Λ-相似类,M的稳定子群为 StabG(M)={S∈G|S-1MS=M}, 对于维数,我们有dimG=dimΟM+dimStabG(M)。 令ind(Ψ)为Ψ中的不可分解矩阵,这里,不可分解矩阵表示非对角矩阵,且inds(Ψ)={M∈ind(Ψ)| dimΟM=s}。 定义2.1[8]ind(Ψ)在群G的作用下的参数数定义为 下面的定理来自于文献[7]定理3.2,推论3.4。 定理2.2ind(Ψ)的参数数μ(ind(Ψ))即为(Ψ,Λ)中矩阵Belitskii标准形中所含参数的极大值,而且(Ψ,Λ)为驯表示型当且仅当μ(ind(Ψ))≤1。 将上述定理应用到二阶矩阵对的约化问题,结合上节计算的Belitskii标准型,我们可以得到下面命题。 命题2.3设(A,B)为二阶矩阵对,其中B=J为Jordan标准形,Ψ为所有二阶矩阵A构成的代数簇,Λ={X∈GLn(k)|XW=WX},则μ(ind(Ψ))=3,因而此线性矩阵问题(Ψ,Λ)为野表示型。
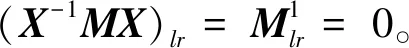
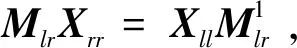
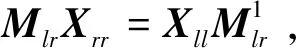
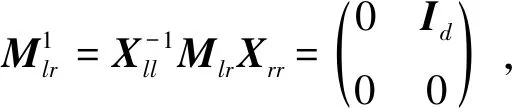
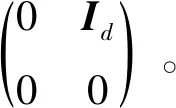

2 二维表示的同构类与参数数
2.1 表示同构类

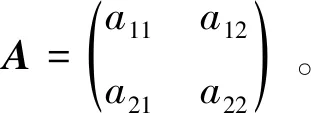
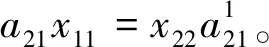
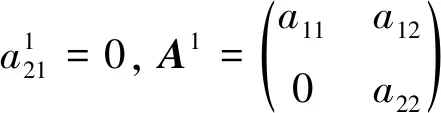
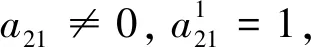
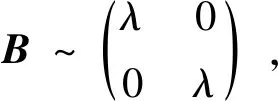
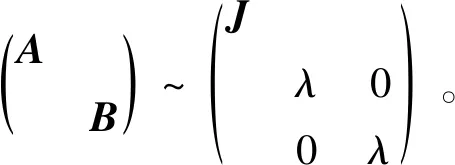
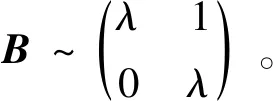


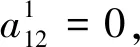


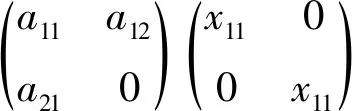
2.2 参数数
