湿空气与水直接接触冷凝CFD模拟研究

2019-04-10段兵兵王恒旭张学军郑幼明

制冷技术 2019年1期

段兵兵，王恒旭，张学军，郑幼明

（1-中国航发湖南动力机械研究所中小型航空发动机叶轮机械湖南省重点实验室，湖南株洲 412002； 2-浙江大学制冷与低温研究所，浙江杭州 310027；3-浙江省博物馆，浙江杭州 310027）

0 引言

空气与水直接接触传热传质是空调系统中的喷水室、化工生产中的换热塔、直接蒸发式的冷却器等设备的基本工作过程，由于其在工业应用中较为广泛而引起人们的重视，大量研究者对空气与水直接接触热质交换进行了研究[1-6]。章立新等[7]研究了用同一水环机组实现供热与制冷两种工作模式时，其终端设备换热塔的特殊工艺要求及传热传质机理。HAWLADER等[8]通过数学模型的数值解获得冷却塔内湿空气的速度、密度、压力以及水温和流量，分析了发生热质交换较为强烈的位置。SOBIN等[9]建立控制方程并结合经验公式研究了水薄层与湍流态的空气逆流进行热质交换的现象，给出了控制方程的近似解，得到了热质交换系数。FEDDAOUI等[10]采用数值模拟的方法对竖直平板通道内空气与水传热传质的现象进行了研究，分析了不同雷诺数和入口参数对热质交换机理的影响。孙银等[11]通过实验研究了新风旁通风量对机组冷凝除湿性能的影响。

尽管有关空气与水直接接触时热质交换的研究已较为深入，但研究点往往集中在空气的温降或者含湿量的增加及其影响因素，对湿空气与水面进行直接接触时发生冷凝除湿过程的研究还较少见。为此，本文将针对流动的空气与水直接接触发生冷凝的过程建立简化的二维数学模型，以分析空气流速、空气相对湿度、水面温度等对冷凝速率的影响。

1 计算模型

流动的空气与水直接接触进行传热传质时，涉及到能量方程、组分运输方程、动量方程和多相流方程，较难收敛，为了便于计算首先作如下假设：

1）水面按固定壁面处理，即忽略水面的波动；

2）湿空气为二元组分混合物，即干空气和水蒸气；

3）各组分为不可压缩理想气体，物性为常数。

1.1 物理模型

根据水槽的实际物理尺寸，将水槽简化为如图1所示的2D模型。方型通道高40 mm，长300 mm，两侧为湿空气进口和出口，底面为冷凝壁面，即实际情况中的水面，顶面为绝热面。

图1 物理模型

1.2 多相流模型

由于在本计算中存在较弱的相间作用，冷凝水极少，且较分散，空气与水的相界面不明显，因此宜采用混合物模型进行求解。在该模型中，用相体积分数来表征各相在控制体内所占的百分比，各相体积分数之和为1。混合物的各项性质和变量由式(1)和(2)计算得出：

式中：

φ——混合物的物理性质；

φi——某一相的物理性质；

αi——某一相的体积分数。

ρ——密度，kg/m3；

λ——导热系数，W/(m…K)；

μ——动力粘度，Pa…s；

cp——比热容，kJ/(kg…K)。

1.3 湍流模型

由于计算模型中的Re数不是很大，因此采用realizable κ-ε湍流模型[12]。近壁面处理选用适宜于低雷诺数和复杂流动的增强型壁面函数。

1.4 蒸发冷凝模型

FLUENT中的蒸发冷凝模型适用于多相流中的混合物模型和欧拉模型，但只能处理纯组分相间的质量传递过程，因此需要编写UDF对其中的参数进行修正，蒸发冷凝模型中的质传递方程：

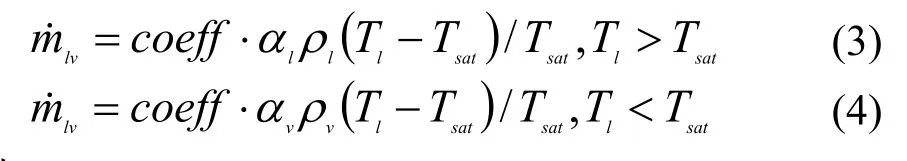
式中：

coeff——蒸发冷凝系数；

T——温度，K；

l、ν、 sat ——液体、气态、饱和态。

从式(3)和(4)可以看出，该系数对于质交换量及潜热交换都有着重要的影响。较大的coeff值会使模型不易收敛，而coeff较小则会导致空气极大的过饱和度，从而增大计算误差[13]。研究中一般根据工作流体的性质、接触面的几何结构及工作参数采用试算的方式来获得合适的coeff值[14-17]，这种方法工作量大，且不具备理论根据。

根据Hertz Knudsen等式，蒸发冷凝通量为：

式中：

F——蒸发冷凝通量，kg/(m2…s)；

β——适应系数；

M——摩尔质量，kg/mol。

R——普适气体常数，J/(mol…K)；

P——压力，Pa；

*——气、液相界面处。

由饱和状态下Clapeyron-Clausius方程可得：

式中：

ν——比体积，m3/kg；

L——相变潜热，J/kg。

上式沿饱和线积分可得：

由式(5)和(7)可得[18]：

由于在混合物和欧拉多相流模型中，流体区域是离散的。假定冷凝过程所有的液滴具有相同的直径dcell，那么气液界面的面积A*可由下式计算：

式中：

A*——气液界面的面积，m2；

Vcell——液滴的体积，m3；

dcell——液滴的直径，m。

因此，冷凝过程中的Hertz Knudsen等式可化为：

结合coeff的定义式可得：

对于湿空气而言，水蒸气与水的饱和温度Tsat为湿空气的露点温度，但由于湿空气的露点温度是由水蒸气的分压决定的，因此需要在UDF中计算实际湿空气的Tsat值，此时，M为水蒸气的摩尔质量。

2 控制方程

对于第i组分，其连续性方程如下：

混合物的动量方程：

混合物的能量方程：

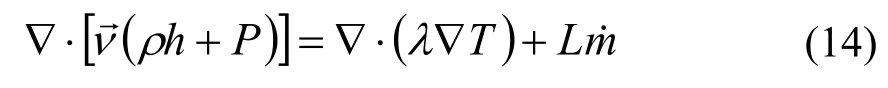
组分运输方程：

式中：

Yi——各组分的质量分数；

h——比焓，J/kg；

Di,m、Di,T——质扩散系数、热扩散系数，m2/s；其中，质扩散系数Di,m可采用动力学理论计算，由于忽略热量扩散作用，热扩散系数Di,T= 0。

3 求解方法

当计算中流体的密度、动量、能量等参数存在相互依赖关系时，宜采用耦合式求解法[19]。流动项采用高阶松弛，松弛因子为0.25，Courant数为200，松弛因子设置参考文献[20]。

4 结果及讨论

4.1 计算结果及验证

图2～图5所示均为单一工况的计算结果。该工况下进口处空气的温度为25 ℃，相对湿度为60%，流速为0.5 m/s，壁面温度为7 ℃。无量纲壁面距离y+为0.15，满足增强型壁面函数的κ-ε模型对y+的要求[21]。由图2知，速度处于入口段，在整个空气流向上并没有形成稳定的速度边界层，空气主流速度在流出前一直增大。从图3、图4可见，湿空气在流过一段距离后便已形成稳定的温度和浓度边界层，温度和水蒸气浓度在y方向上的分布不再随x变化，温度边界层较浓度边界层更厚。从图5中可以看出，空气的冷凝速率开始就很大，然后逐渐减小，稳定后的速率仅为最大值的20%。

图2 y方向上空气速度分布

图3 y方向上空气温度分布

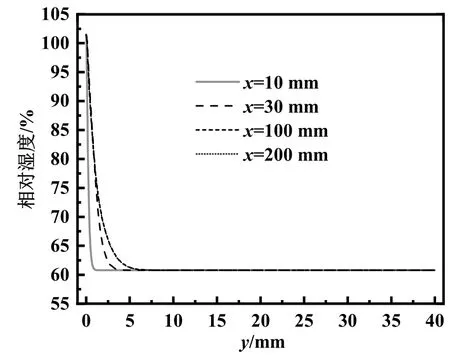
图4 y方向上湿空气相对湿度分布

图5 冷凝速率和传热系数在x方向上的变化趋势

达到稳定后，模拟得到的空气与水之间的对流换热系数及冷凝速率分别为24.58 W/(m2…K)、1.13×10-4kg/(m2…s)。采用文献[22]中的经验公式计算，当对流换热系数为24.58 W/(m2…K)时，冷凝速率为1.4×10-4kg/(m2…s)，误差为-21.4%；采用不同的进口空气流速进行验证，对比结果如图6所示。

可见其变化趋势完全一致，平均相对误差为-21.1%。由此可见，模型符合实际情况，但其精确度仍有待于提高。从蒸发冷凝模型中的冷凝系数的设置来看，造成计算结果较小的直接原因是冷凝系数选取仍然偏小，使得相同条件下的冷凝速率偏小。由于继续增大冷凝系数时计算不易收敛，因此，本文仍然采用原冷凝系数的设置进行后续计算。

图6 结果验证

4.2 进口空气参数的影响

本文分析了进口空气流速、相对湿度对冷凝速率的影响。图7和图8分别为空气流速在0.1 m/s～1.0 m/s下湿空气的冷凝速率、除湿量及每千克空气减少的含湿量Δd。从图7可以看出，随着空气流速增大，空气质量流量增大，由于对流换热系数增大，冷凝速率呈增长趋势，空气通过流道后的除湿量也随之增大。但是，从图8中也可看出，当流速小于0.3 m/s时，随着流速增大，Δd减小十分明显，当流速大于0.3 m/s时减小的趋势逐渐变缓。

图9所示为冷凝速率随进口空气相对湿度的变化趋势。由于空气中水蒸气的浓度更大，扩散到壁面附近的水分子数更多，因而冷凝速率越大，这一现象在空气流速增大时更为明显。因此，当某空间内要求的相对湿度较大时，为维持相对湿度的稳定性，应采用较小的风速，避免因除湿量过大而造成相对湿度在大范围波动。

图7 进口空气流速对冷凝速率的影响

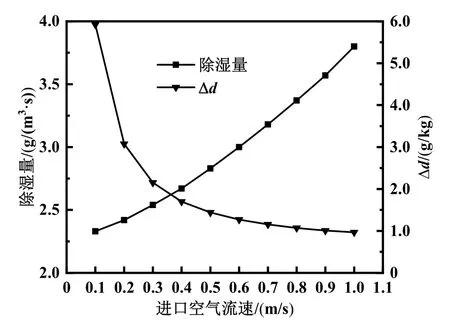
图8 进口空气流速对除湿效果的影响

图9 进口空气相对湿度对冷凝速率的影响

4.3 水面温度的影响

由于壁面温度即代表了水面的温度，因而其对冷凝速率的影响十分重大。图10所示为不同进口空气流速下冷凝速率随壁面温度的变化趋势。可以看出，当进口空气的参数一定时，壁面温度存在一个临界点，当壁面温度低于该临界点时，壁面温度继续降低对于冷凝速率的影响不大，而当壁面温度高于临界点，冷凝速率大大降低。微观上看，由于温度边界层比浓度边界层厚，因而壁面温度决定了浓度边界层内的温度分布，当壁面温度较高时浓度边界层上方空气未饱和，因而冷凝只发生在浓度边界层的下部分。但在流速变化范围不大时，临界温度变化不大。因此，对于一定状态的进口空气，采用临界温度的水进行冷凝除湿能够最大化除湿速率。

图11所示为不同相对湿度下壁面温度对冷凝速率的影响。可见，在不同的相对湿度下，临界温度也不同；当空气相对湿度较低时，临界温度较小。由于空气温度变化时，会影响相对湿度，因此分析温度的影响时，假定空气的含湿量不变，此时空气的露点温度相同。

图10 不同流速下壁面温度对冷凝速率的影响

图11 不同相对湿度下壁面温度对冷凝速率影响

不同入口空气温度时壁面温度对冷凝速率的影响如图12所示，当壁面温度较高时，空气温度变化基本不影响冷凝速率。当壁面温度低于当前温度下的临界温度时，冷凝速率达到最大值后基本不再变化；且温度越高，临界壁面温度越低。

图12 不同进口空气温度下壁面温度对冷凝速率影响

综合比较不同温度和相对湿度下壁面温度的影响，可以发现：临界壁面温度取决于空气温度边界层与水蒸气浓度边界层之间的关系。当空气温度一定时，温度边界层厚度一定，此时空气相对湿度越高，则在低于空气露点的温度范围以内水蒸气的浓度越大，自然冷凝速率就越大；当空气露点温度一定时，水蒸气的浓度边界层结构及分布是一定的。此时，冷凝速率取决于水蒸气浓度边界层内的温度分布。若水温较高，在浓度边界层范围内温度分布较为接近；当水温较低时，随着空气温度变高，温度梯度更大，浓度边界层内低于空气露点温度的区域变少，因而冷凝速率达到最大。