固空沉积的数值模拟
2019-04-10周伟煜梁文清钱华雷刚荀其宁
周伟煜,梁文清*,钱华,雷刚,荀其宁
(1-东南大学能源与环境学院,江苏南京 210096;2-航天低温推进剂技术国家重点实验室,北京 100028; 3-国防科技工业应用化学一级计量站,山东济南 250031)
0 引言
随着航天事业的发展,液氢作为一种高比冲特性的环境友好性推进剂组元,其应用水平和应用规模有了极大的提高。而在推进液氢工业化过程中,液氢系统安全性问题显得尤为重要。液氢系统在液氢加注、气氢排放、系统吹除置换中,都极易造成少量空气的渗入。氮、氧在液氢中溶解度低,液氢中固空的积累不可避免。而固空中氮氧比例分布是影响固空安全性的重要因素[1]。
国外开展的固空爆炸试验研究表明,当固空中氧体积分数大于空气中氧体积分数时,会有爆炸甚至爆轰危险[2]。国内刘海生等[3-4]开展固空理论和实验研究,通过掺杂-复温-气相色谱检测的方式得到固空颗粒表面富氧、内部贫氧的结论。在理论研究方面,通过对比微观下氮氧分子间吸引能得到与试验相一致的结论。这些研究仅能对固空中氧分布进行定性描述,而未给定量结果。由于实验研究难以对氮氧成分进行定量探究,故采用凝固模拟来解决固空沉积氮氧分布问题。
目前已有较多关于相变过程的模拟及实验研究。齐隽楠等[5]研究了疏水和亲水竖直圆柱面上的滴状冷凝特性以及膜状冷凝特性。郭亚等[6]建立三分螺旋折流板冷凝器模型,并模拟对比了单、双头变角度三分螺旋折流板与变间距弓形折流板立式冷凝器的凝结换热性能。胡海涛等[7]建立金属平片冷表面湿空气凝水过程热质传递特性的数值模型。黄飞等[8]提出了外科手术冷冻过程的动态模型。而凝固领域较常采用主要有相场(PF)模型[9-10]、元胞自动机(CA)模型[11-12]。邹阳等[13]采用相场法模拟制冷剂中冰晶的生长过程,结果与实验现象较为吻合。与相场模型相比,元胞模型计算效率更高,并在ZHU等[14]的改进下已具备定量模拟能力。对于流场部分,格子玻尔兹曼(LBM)因其效率高、并行能力强、易处理复杂边界的特点,更适用于介观尺度下的流场计算。康利云等[15]通过建立LBM传热模型,计算泡沫多孔材料有效导热系数,具有较高精度。
本文采用格子玻耳兹曼和元胞自动机相结合的模型,并结合氮氧凝固相图研究固空凝结过程中具体的氮氧体积分数分布,讨论过冷度、初始氧体积分数和自然对流对凝固的影响。
1 数学模型
实际情况下,空气进入液氢后转变为固空的过程可能有两种,一种是先冷凝后凝固,另一种是凝华。为简化分析,仅考虑氮氧混合液在一定过冷度或冷却速率下的凝固过程。凝固过程同时涉及溶质场、温度场的变化,氮氧混合液物理参数也会相应地变化。若全面考虑凝固对物理参数的影响,将极大地增加计算量,因此在模拟中对相关参数进行简化处理。
同时为保证流场计算的稳定和效率,作如下假设:1)液相为不可压牛顿流体;2)固液两相热扩散系数相等且为常数;3)忽略温度和体积分数变化对液相的影响;4)忽略晶体在液相中的移动。
1.1 LBM模型
本文采用基于LBGK近似的LBM模型用于计算流场,其演化方程为:
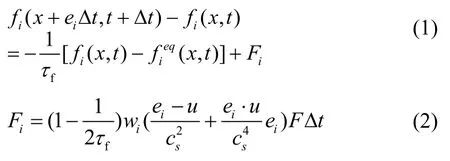
式中:
fi(x,t)——粒子分布函数;
Δt——时间步长,s;
ei——离散速度,m/s;
τf——无量纲松弛时间;
Fi——离散速度空间外力源项,N;
cs——格子声速,m/s,即
c——格子速度,其值为1 m/s;
F——外力项,N,在本研究中具体为因体积分数差及温差产生浮力作用。
根据Boussinesq近似,浮力项可表示为[16]:
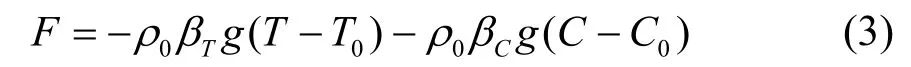
式中:
ρ0——初始密度,kg/m3;
βT——温度膨胀系数,K-1;
βC——体积分数膨胀系数,vol-1;
g——重力加速度,m/s2;
C0——初始体积分数;
T0——初始温度,K。
类似地,体积分数场及温度场计算方程也可以转换成对应的LBM演化方程,具体表达式为:
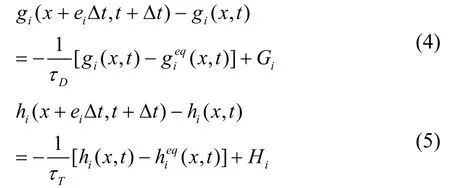
式中:
gi(x,t)——体积分数分布函数;
hi(x,t)——温度函数;
τD、τT——体积分数场及温度场的松弛时间;
Gi、Hi——凝固过程中一个时间步长释放的溶质和潜热后增加的体积分数及温度源项。
流场、体积分数场、温度场的松弛时间可分别由动力黏度ν、氧的扩散系数D1、热扩散系数α求得,即下式:

该模型的宏观密度ρ、速度u、体积分数Cl、温度T定义如下:
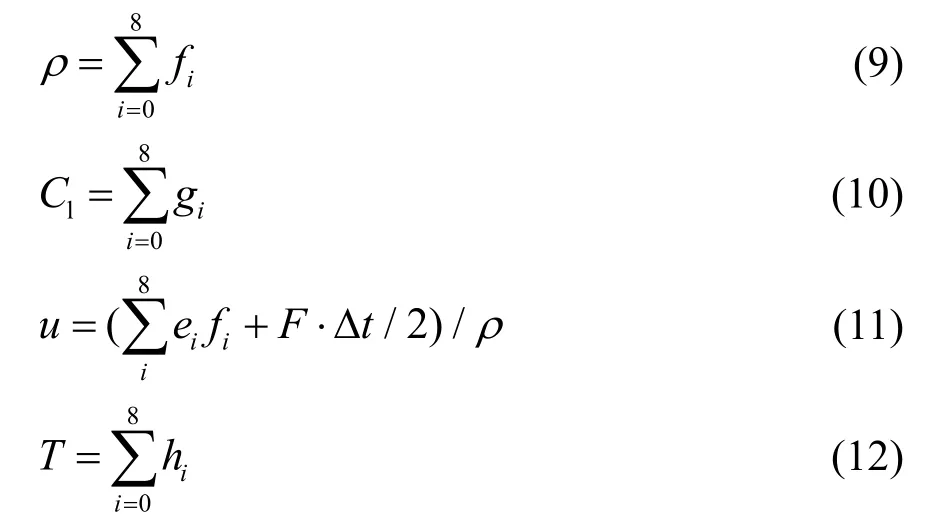
本文采用D2Q9离散速度模型,其速度配置为:
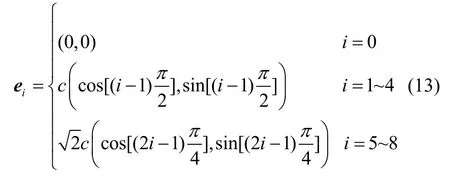
由此可确定粒子、体积分数及温度平衡态分布函数为:
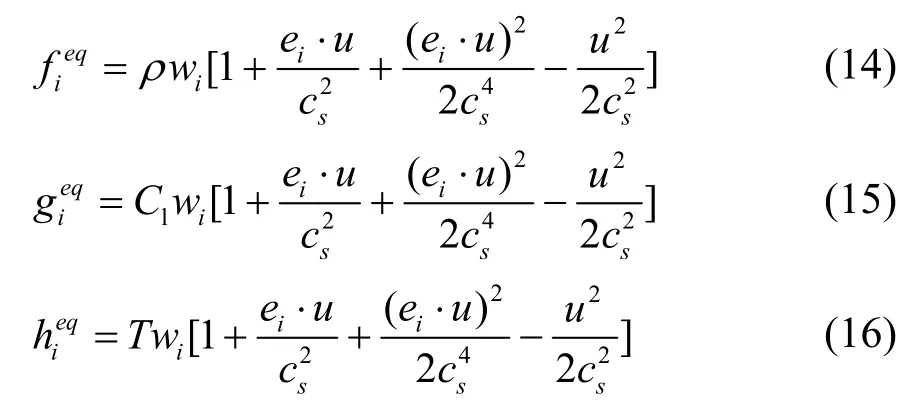
式中,wi为权系数,与离散速度方向相对应的值为w0=4/9,w1-4=1/9,w5-8=1/36。由上述(1)~(16)可耦合流场、体积分数场、温度场。而研究中采用被动标量法,通过速度场u的改变继而更新式(15)和式(16),从而体现流场对体积分数及温度场的影响。
1.2 CA模型
根据ZS模型[17],凝固生长的驱动力来源于界面处实际体积分数与平衡体积分数之差。在界面处过冷度由热过冷、成分过冷、曲率过冷组成,并满足热力学平衡,由此得到界面处平衡体积分数:
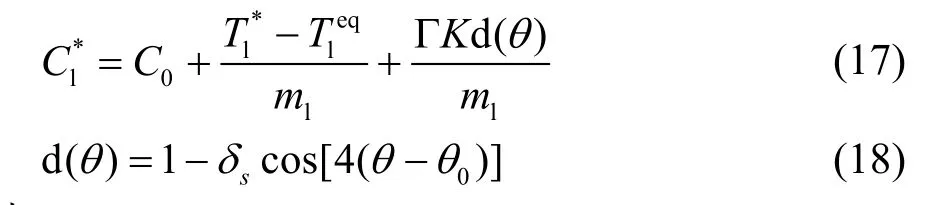
式中:
C1*——界面元胞平衡体积分数;
C0——初始氧体积分数;
T1*——界面元胞温度,K;
T1eq——初始氧体积分数所对应的液相线温度,K;
m1——液相线斜率;
Γ——Gibbs-Thomson系数,m…K;
d(θ)——界面能各向异性函数,此处考虑到氮氧晶体在低温下呈现立方晶体形状;
δs——表面能各向异性强度;
θ0——择优生长方向与x轴的夹角,°;
K——界面曲率,m-1,根据其物理意义表示为:
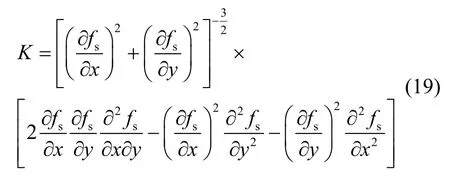
由式(19)可得到ZS模型中界面前沿新增固相分数,同时控制固相分数不大于1,得到单位时间新增固相分数sdf计算式(20)和式(21):


由此可以得到式(4)和式(5)中体积分数源项Gi及温度源项Hi:
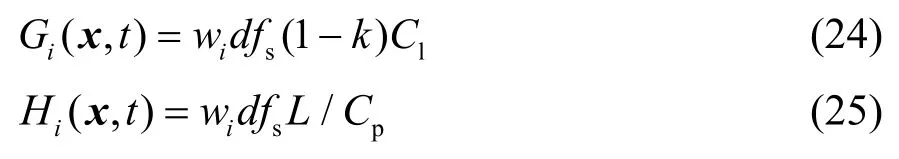
式中:
k——溶质再分配系数;
C1——氮氧混合液中氧份数;
L——氮氧混合液凝固潜热,kJ/kg;
Cp——氮氧混合液定压比热容,kJ/(kg…K)。
1.3 CA与LBM的耦合
在凝固初始阶段,在凝固场中放置一个氮氧晶粒,固相中氧体积分数为kC0,其余区域充满过冷度为ΔT0的过冷氮氧混合液。由于氧在液氮中扩散系数是其在固氮中扩散系数的103数量级,因此忽略氧在固态晶体中的扩散过程。随着凝固前沿不断推进,界面元胞析出溶质氧至前沿,同时释放潜热产生温度增量,造成体积分数和温度分布不均,最终导致凝固场密度不均。低密度液相上浮,高密度下降,产生自然对流。而对流对晶体生长的影响主要通过速度u改变体积分数、温度分布函数,进而影响晶体生长。具体物理参数的设置见表1,为简化计算,忽略温度等对相关物理量的影响而设为定值。
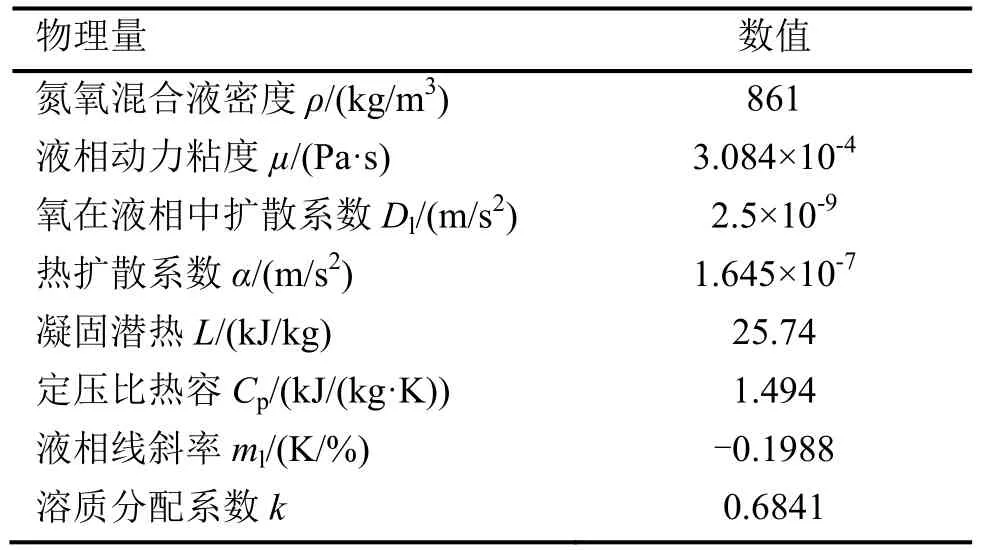
表1 模拟所用物性参数[18]
1.4 边界条件
氮氧凝固场边界条件见图1,四周为恒壁温边界,温度恒定为T0,采用非平衡态外推格式实现;体积分数设为无扩散边界,即流场设为无滑移边界条件,即ux=uy=0,也通过非平衡态外推格式计算。当晶体逐渐生长呈复杂形貌时,流场与晶体间的固液(S/L)界面设为无滑移边界,并用反弹格式处理。忽略氧在固相中的扩散作用,氧分子无法以扩散形式通过S/L界面,故同样采用反弹格式处理界面体积分数边界。
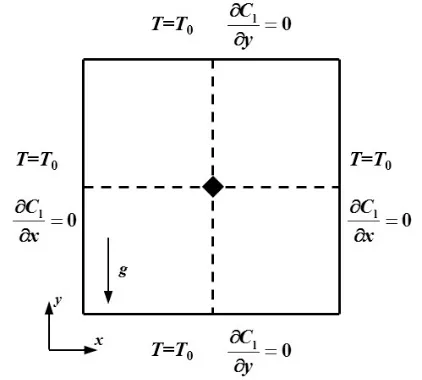
图1 凝固场边界示意图
2 结果与分析
2.1 纯扩散下氮氧晶粒的生长
为研究空气比例的氮氧混合物在凝固过程中体积分数分布,模拟时取氮氧混合液中初始氧体积分数为C0= 0.21,温度过冷度ΔT0= 0.8 K,界面能各向异性系数δs= 0.2,Gibbs-Thomson 系数Γ = 1.0×10-7m…K,Δx = 3×10-7m,整个凝固场划分300×300个均分网格。图2为固相率为0.04时氮氧晶体形貌及氧体积分数分布,可见氮氧晶体在形貌和体积分数分布上均呈现四方对称性。随着凝固的进行,界面处不断析出溶质,而氧在液相中的扩散系数较小,因而无法及时扩散,在外沿处形成一层氧的高体积分数区。由于研究中将界面体积分数与平衡体积分数差C1-C1eq作为凝固驱动势,凝固生长出的晶体臂阻碍中间区域氧的扩散,因而氧在根部富集形成“颈缩”现象[19]。相反地,晶体臂前端析出的氧更易与大空间低体积分数区接触,故生长较为迅速。
图3为不同凝固时刻下y=0.019 µm处氧体积分数分布图。图中所示的曲线图呈现中间低两边高的“凹”字形特征,即中间贫氧、外部富氧。分析可知两侧外侧氧体积分数恒定为0.21,此处为未发生凝固的液相。随着凝固时间延长,S/L界面推移,高体积分数所对应的位置向两侧移动,外侧恒定体积分数区域缩短。从外侧环境体积分数至体积分数峰值之间形成一定的体积分数梯度,由氧的有限扩散能力所致。当内侧经过高浓度界面处后,体积分数骤然下降,这是由于晶体界面厚度一般为纳米级,实际工程中可以忽略。采用的CA模型为尖锐界面模型,忽略界面厚度,故内侧低体积分数即为固态晶体中氧体积分数值。此外,y = 0.019 µm处氧体积分数最高为0.244,而在整个凝固场体积分数最高值为0.273,均已超过LITCHFIELD等[20]通过枪击试验所得到氧体积分数安全阈值0.24,存在爆炸风险。凝固前沿与低体积分数液相接触面积大,且体积分数势差较大、扩散快,因而凝固时间对于体积分数峰值及固相中氧体积分数影响均不大。
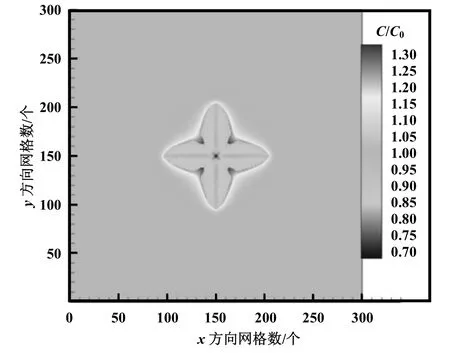
图2 氮氧晶体形貌及凝固场氧体积分数分布图
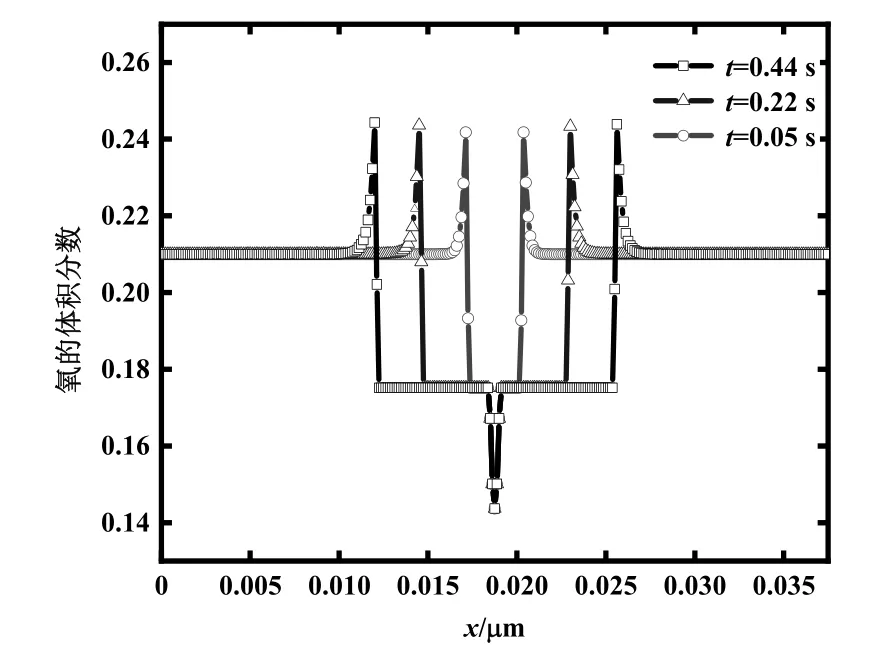
图3 不同时刻下y = 0.019 µm处氧体积分数曲线
2.2 初始氧体积分数的影响
为研究不同初始氧体积分数对于氮氧晶体形成的影响,模拟中选取3个不同初始体积分数C0分别为0.20、0.25和0.30,控制初始过冷度为ΔT0=0.8 K,并以凝固速率以及氮氧体积分数分布为研究对象。
由图4可见,固相率随时间以近似正比关系增长。固相率随时间增长斜率可视为凝固速率。C0=0.20、0.25、0.30下凝固速率对应为0.135 K/s、0.042 K/s、0.023 K/s。随着初始氧体积分数的增加,凝固速率却下降。当凝固时间为0.44 s时,C0=0.20对应的固相率为0.044,而此时C0=0.30所对应的固相率为0.011,两者相差3倍。这是由于凝固时析出的氧在晶体表面富集,初始体积分数越大意味着晶体界面附近体积分数值越高。在扩散系数一定的条件下,初始体积分数越高,生长越缓慢。由式(20)可知,固相率增量与初始体积分数值成反比关系,因而凝固至相同固相率,初始体积分数越大所需的时间越久。
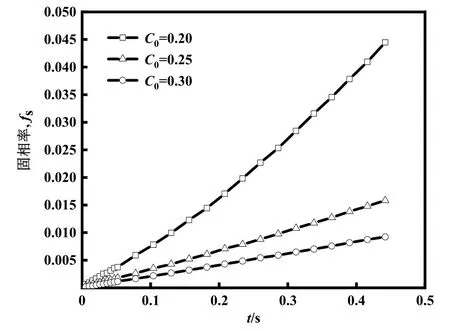
图4 不同初始氧体积分数下固相率随时间变化图
图5中,C0=0.20、0.25、0.30分别对应的体积分数峰值为0.23、0.28、0.34,固相体积分数为0.17、0.20、0.23。由此可见,初始体积分数对体积分数峰值及固相体积分数的影响程度几乎一致,同时可推测氧体积分数峰值Cmax正比于C0,若固空中氧体积分数安全阈值为0.40,则混入的氮氧混合物杂质中氧体积分数应小于0.34。
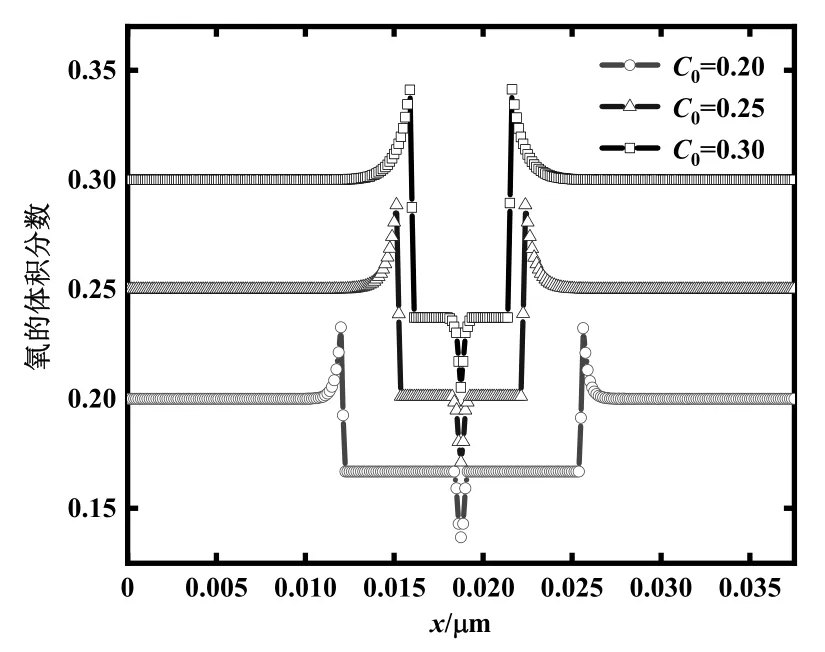
图5 不同初始氧体积分数下y = 0.019 µm处 氧体积分数分布变化图
2.3 初始过冷度的影响
为研究不同初始过冷度对于氮氧晶体形成的影响,模拟中选取3个不同过冷度ΔT0=0.5 K、0.7 K、0.8 K,控制初始氧体积分数为C0=0.20,并以凝固速率以及氮氧体积分数分布为研究对象。
由图6可见,随着初始过冷度的增加,凝固速率迅速上升。相同凝固时间为0.44 s,ΔT0=0.8 K时固相率为0.044,而ΔT0=0.5 K时固相率仅为0.006,两者相差约7倍。ΔT0=0.5 K、0.7 K、0.8 K凝固速率分别为0.017 K/s、0.054 K/s、0.135 K/s。由此可见,过冷度相比于初始体积分数对于凝固速率的影响大得多。从式(17)可以看出,温度对于凝固的影响体现在ΔT/ml,而体积分数影响主要体现在C1-C1eq上,而液相线斜率ml小于1,故数值上温度变化影响较初始体积分数更大些。
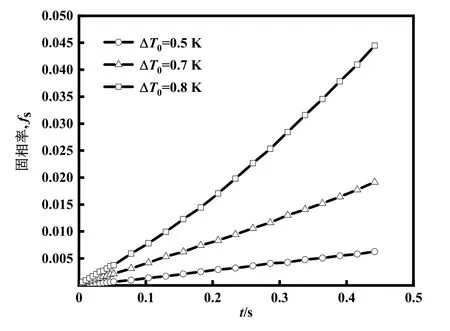
图6 不同过冷度下固相率随时间变化图
从图7可见,初始过冷度增加,凝固生成的固相中氧体积分数也增加,而对于凝固场体积分数峰值,ΔT0=0.5 K时峰值最小,ΔT0=0.7 K和ΔT0=0.8 K时峰值几乎一致。由此可以推测相同初始成分氮氧混合物,过冷度增加时,晶体外沿的氧体积分数增加,此时安全风险越大。
2.4 自然对流的影响
当将晶体凝固过程中引发的自然对流考虑在内时,从图8可见,晶体呈非对称性生长。凝固初期,计算域内体积分数和温度差异不大,因而自然对流强度较弱,区域内流速较小。从图8(a)中流线上看,左右侧分布有两个涡,流线相对称。此时氮氧晶体近似于纯扩散时生长,在4个方向上生长程度相近。经过一段时间后,明显下侧方向生长较上侧快,上侧几乎不生长。这是由于自然对流由密度差造成,而密度差的产生源于凝固过程中氧体积分数差及温度差。凝固中不断释放的热量和析出的溶质使界面温度和体积分数持续上升,促进了自然对流的增强。对流也影响体积分数和温度的分布,使高氧体积分数、高温度的流体上浮至流场上游,抑制晶体上端部分生长。而下游的氧体积分数较小温度较低,更利于晶体的生长。从图8(d)流线可看出,随着晶体左右两侧的生长,流场将在晶体臂的阻隔作用下由原来的2个涡转变为4个涡。因而自然对流对氮氧晶体凝固形态产生重要影响,也强化了溶质和热量的传输,导致竖直方向体积分数梯度较水平方向的梯度大得多。下面以x=0.019 µm处的体积分数分布研究自然对流对氧体积分数峰值及氮氧分布的影响。

图7 不同过冷度下y=0.019 µm处氧体积分数分布变化图
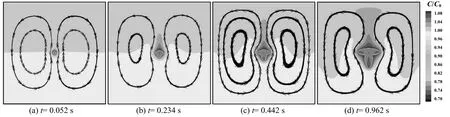
图8 不同时刻下自然对流凝固场氮氧晶体形貌氧体积分数分布图
从图9可以看出,自然对流下固相范围比纯扩散时小。这是因为晶体凝固生长驱动力主要来源于成分过冷和热过冷,而在氮氧凝固时热过冷相比于成分过冷,数值上更具主导性。在纯扩散中将计算区域温度视为恒定过冷度,而实际凝固时释放潜热产生温度增量,在冷却速率有限时,将引起全场平均温度升高,抑制晶体平均生长速率。因此尽管自然对流促进氧分子在液相中的扩散,界面体积分数下降,但成分过冷对生长促进程度不足以弥补温度升高而产生的抑制作用。另一方面,下游较上游固相区域更大,这与此前分析结果一致。在氧体积分数分布方面,自然对流降低界面氧体积分数梯度,促使整个计算液相中氧趋于一致。最高氧体积分数位于上游界面处,约为0.23,界面上下游峰值体积分数差约0.01。
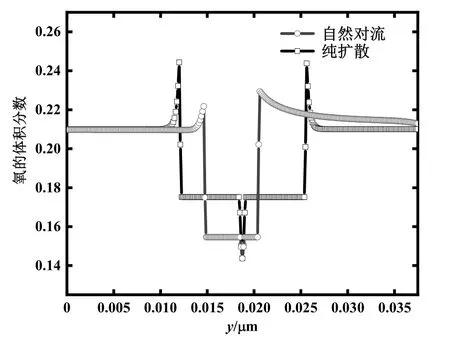
图9 纯扩散和自然对流下x=0.019 µm处氧体积分数对比图
3 结论
1)本文建立CA-LBM模型,模拟单个氮氧晶体在一定过冷度下生长过程,并研究晶体生长形貌以及凝固场氧体积分数分布情况。在氮氧混合液氧体积分数为空气中比例时,新生成的晶体呈内部贫氧、外部富氧,这与刘海生等[3]所得实验结果一致,而晶体界面处局部体积分数峰值已达0.244,存在一定安全风险。
2)模拟单个氮氧晶体在不同过冷度、不同初始氧体积分数条件下的生长,分析得到凝固速率及凝固场氧体积分数峰值随过冷度增大而增大;初始氧体积分数越大,凝固速率越小,氧体积分数峰值越大。
3)将自然对流考虑在凝固过程中,发现晶体呈非对称性生长,上游较下游生长缓慢。自然对流使晶体凝固速率下降,同时内部流场的存在使得整个凝固场的氧体积分数趋向均匀。一定过冷度下,与纯扩散相比,自然对流下晶体内部氧体积分数减小,界面处氧体积分数峰值也下降,但外部流场平均体积分数上升。
