微波连续变量极化纠缠*
2019-04-10罗均文吴德伟李响朱浩男魏天丽
罗均文 吴德伟 李响 朱浩男 魏天丽
(空军工程大学信息与导航学院,西安 710077)
(2018 年10 月26 日收到; 2018 年12 月4 日收到修改稿)
极化微波作为当前被广泛应用的信息载体,具有许多独特的优势. 随着超导技术的发展,量子微波技术逐渐兴起,将量子纠缠应用于极化微波将具有广阔的应用前景. 本文阐述了连续变量极化纠缠的原理,提出了极化纠缠微波方案并进行了仿真分析,利用归一化的不可分度I作为判据,分析了在整个约瑟夫森混合器100 MHz 工作带宽内斯托克斯参量的不可分度I (,) ,I (,) ,并进一步分析了I分别与压缩度r、振幅比值Q的关系,发现I (,) ,I (,) 分别对振幅比值Q、压缩度r的变化敏感,且在本文研究的条件下I (,)始终大于1,I (,)始终小于1,斯托克斯参量,构成不可分态,方案产生的两个微波信号和 存在二组分极化纠缠,最佳纠缠出现在70 MHz 附近,此时I (,) 取得最小值0.25.
1 引 言
近三十年来,量子信息技术发展迅猛,纠缠资源作为量子力学的核心,其性质得到了广泛的研究与应用[1,2]. 根据观测量的不同产生了不同的纠缠类型,如正交分量纠缠、极化纠缠等[3,4]. 极化是电磁波的一个重要性质,广泛应用于雷达、导航、通信等领域,且表征极化状态的斯托克斯参量探测时不需要本地振荡信号,相较正交分量纠缠的探测更为容易,因此极化纠缠的实现对于纠缠的应用具有重要的意义.
早期的极化纠缠是由光子对实现的,属于离散变量的极化纠缠[5]. Bowen 等[6]提出了连续变量光极化压缩及纠缠,将斯托克斯参量量子化,提出了相应的测量方案和纠缠判据,且进行了实验验证.Korolkova 等[7]使用超短脉冲源和克尔非线性效应实现了1550 nm 波段的连续变量极化纠缠.Guo 等[8]研究了连续变量轨道角动量的压缩和纠缠,同样分析了轨道角动量的斯托克斯参量,使用的分析方法借鉴自连续变量极化压缩与纠缠. 吴量等[9]在795 nm 波段进行了两组分极化纠缠光场的实验制备,并认为该极化纠缠光场可应用于未来的量子存储,实现量子通道和量子节点之间、两个量子节点之间的纠缠以及量子态的传输,之后该小组又基于极化分束网络实现了三组分的极化纠缠光场[10]. 周瑶瑶等[11]研究了镀膜参数差异对连续变量纠缠度的影响.
由于可见光波段的光子具有较高的能量,且对应探测器工作条件友好,因此目前有关的极化纠缠均通过可见光实现. 相较于可见光,微波波段会受到光子能量较低、器件工作条件苛刻等不利因素的影响[12],但同时具有更长的相干时间、与现有超导器件的良好兼容性以及信号可放大、可中继的强大优势[13],因此近年来成为了量子纠缠研究的一个热点[14−16].
本文从理论上分析了两组分极化纠缠的产生、探测原理,提出了一种微波连续变量极化纠缠的可能实现方案并进行了仿真,得到了极化纠缠的微波信号斯托克斯参量,与之间的不可分度,分析了压缩度r、极化分量振幅比值Q分别同不可分度I的关系,并探讨了正交分量纠缠与极化纠缠的转换关系.
2 基本原理
任意电磁波的极化状态可以由四个斯托克斯参量完全描述,分别记为S0,S1,S2和S3,而量子化的斯托克斯参量使用算符表示为,,和[17]. 在经典电磁波中,电磁波可以分解为水平极化分量EH和垂直极化分量EV[18],也就是

其中,EH和EV分别是水平极化分量和垂直极化分量的振幅,ϕH和ϕV表示对应的相位,则相位差ϕ可表示为
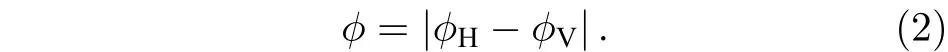
将电磁场量子化后,电磁波的水平极化分量用表示,垂直极化分量用表示,则可将斯托克斯算符展开为
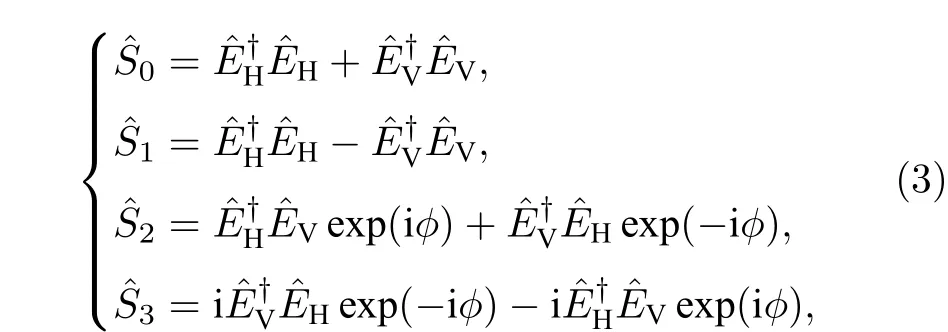
同时,四个参量满足对易关系:

当EV≫EH时,结合不确定性原理以及正交分量量子起伏,并认为,的量子起伏不相关,忽略干涉项,可以得到斯托克斯参量的均值和量子起伏为
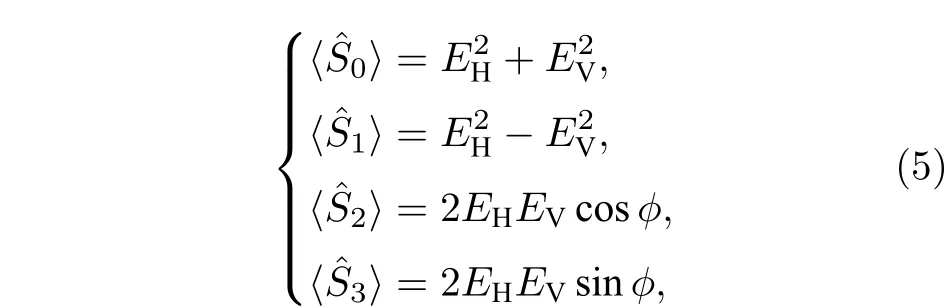

(6)式中,δ为水平(垂直)极化分量的正交振幅量子起伏,δ为水平(垂直)极化分量的正交相位量子起伏.
极化纠缠可以通过转换正交分量纠缠而得到,即将两路正交分量纠缠的信号与两路强相干态信号分别在不同的极化分束器件上耦合,所产生的两路输出表现为极化纠缠,其原理如图1 所示. 正交分量纠缠信号,作为水平极化分量,与强相干态信号,分别在极化分束器件上合成,得到两路极化纠缠信号,,其纠缠特性的具体观测量为,的斯托克斯参量. 在极化纠缠探测部分,直接使用两套相同的平衡零拍探测装置,通过对探测器输出电流作加减法得到两路信号的,参量. 由(3)式可知,两路信号,参量的测量必须进行极化偏转,同时引入额外相位,完成基变换,使得两参量能够对应物理可观测量,如电流,然后再使用平衡零拍探测装置进行测量.因此,测量时需要在极化分束器(PBS)前加入一个与水平方向成45°角的半波片,再经平衡零拍探测装置探测,而测量则需要在测量的基础上,在半波片后加上一个与水平方向成22.5°角的1/4 波片. 这样便可将所有斯托克斯参量测出,进而分析各斯托克斯参量的性质.
正交分量纠缠中使用段氏判据[19]验证两路信号纠缠与否,为了验证二组分极化纠缠,需要对段氏判据进行拓展,使之能够验证斯托克斯参量间的二组分纠缠. 以下标a,b区别观测量所在信号,则正交分量纠缠的段氏判据可表示为

为简单起见,本文均用形如 ∆2() 的式子表示 m in[∆2(+),∆2()] . 根据标准不确定性关系,对于任意一对可观测量M和N,可以将段氏判据拓展为(参阅附录A)


图1 两组分极化纠缠光场生成及探测原理图(OPA,光参量放大器; BS,分束器; PBS,极化分束器; D,探测器)Fig. 1. Scheme of preparation and measurement towards bipartite polarization entangled optical fields. OPA,optical parametric amplifier; BS,beam splitter; PBS,polarization beam splitter; D,detector.
为方便对数据进行讨论,可将判据归一化,从而得到二组分纠缠的不可分度(inseparability):
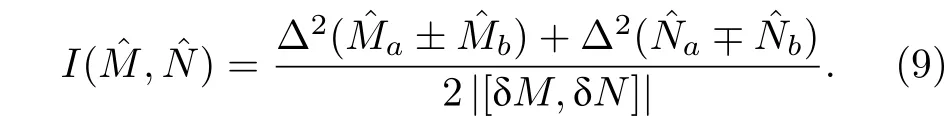
当I(,)<1 时,说明对应M和N这对观测量,量子态不可分,信号1 和信号2 纠缠. 因此,斯托克斯参量中除外,,和间的不可分度可表示为
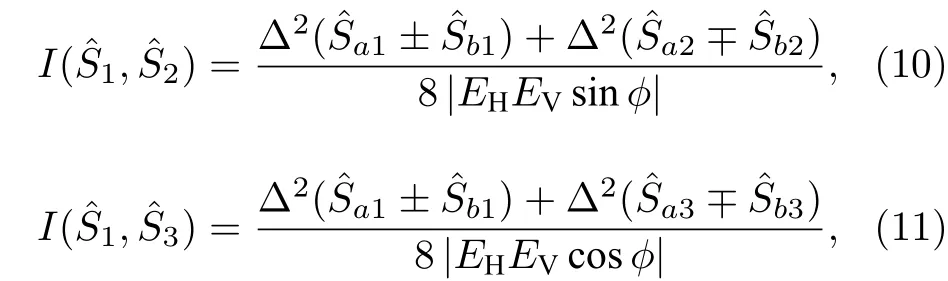
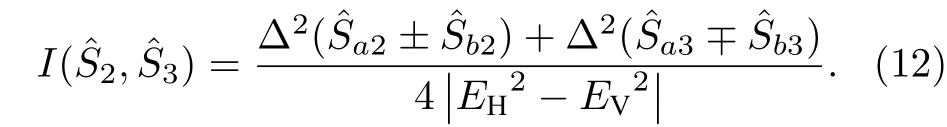
显然,从(10)—(12)式可以看出,在某些取值情况下,可能无法同时获得三个不可分度,因此不可分度只是一个充分不必要条件,这是由于标准不确定性关系中去除了关联项引起的.
3 方案设计与结果分析
借鉴可见光波段实现极化纠缠的方案,提出了一种微波波段极化纠缠方案,其原理如图2 所示.
如图2 所示,在极化纠缠生成部分,使用一个约瑟夫森混合器(Josephson mixer,JM)[20]对两输入信号,进行双模压缩,使得
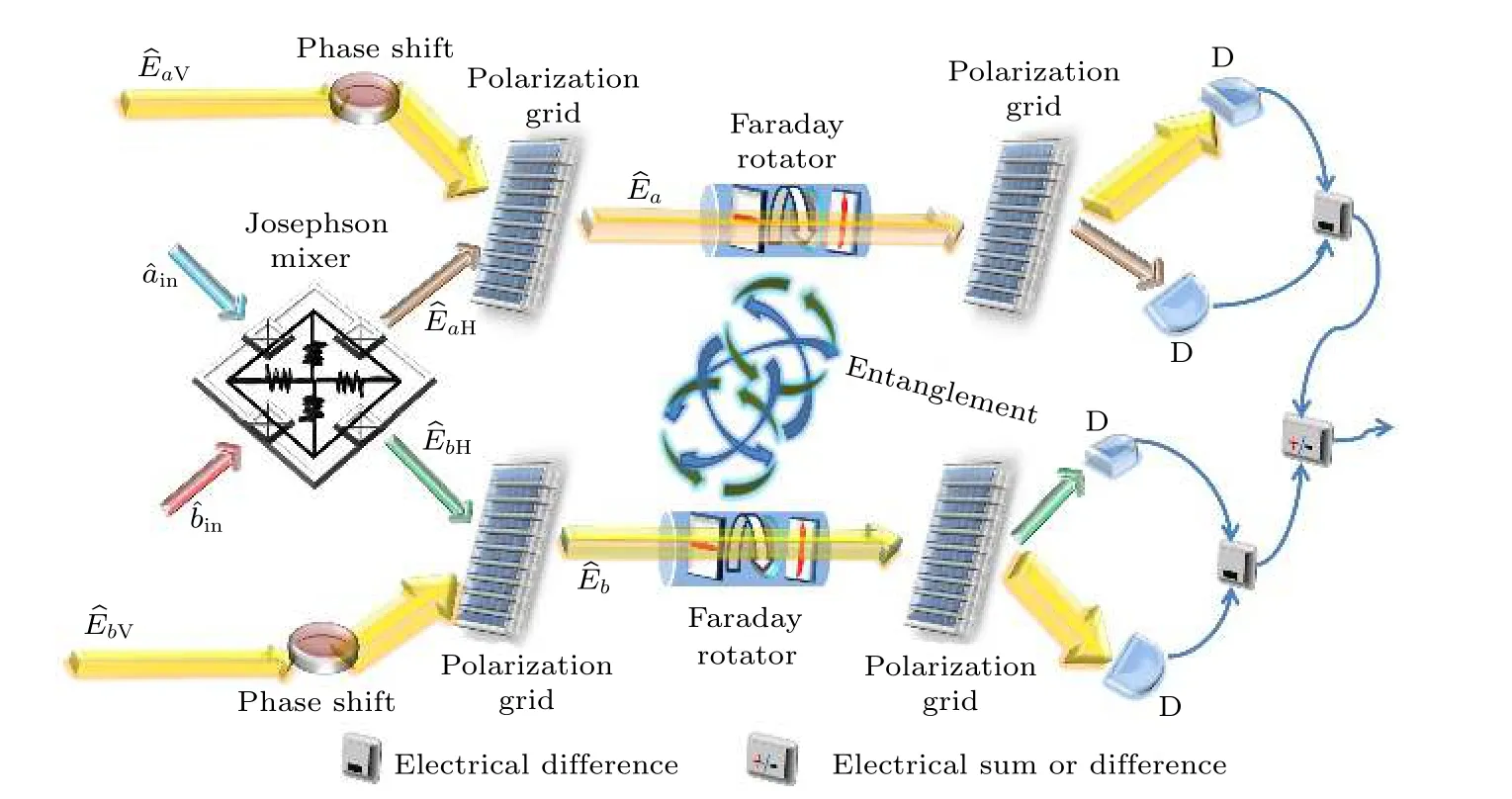
图2 二组分极化纠缠微波方案示意图(D,探测器; 方案整体工作温度为0.5 mK)Fig. 2. Schematic of bipartite polarization entangled microwave. D,detector. Overall operation temperature of the proposal is 0.5 mK.

此时输出信号是正交分量纠缠的,再将两输出作为水平极化分量,,分别在两个极化栅上与垂直极化的强相干态微波信号,耦合,形成极化纠缠信号,. 若令两极化分量的振幅比为Q,即Q则其中两个极化分量的振幅和相位满足关系:
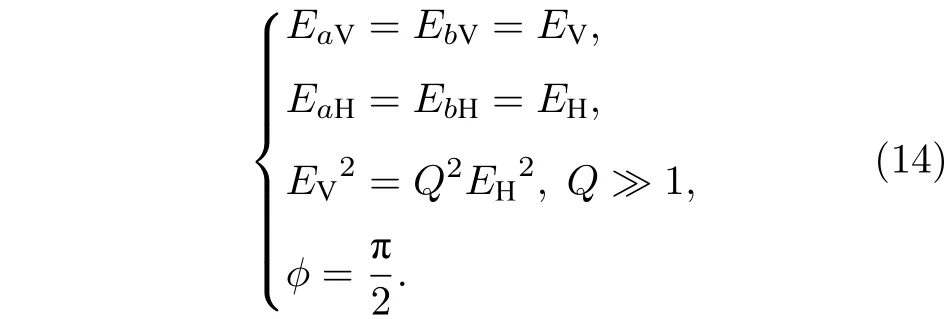
方案部分参数设定如表1 所列.
在表1 所列的条件下,,的正交分量间的时域关联如图3 所示. 可以看出,此时两信号的正交振幅正关联、正交相位反关联,且关联性强.
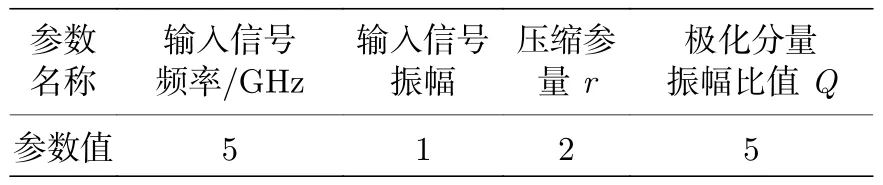
表1 方案部分参数Table 1. Part of the parameters in the scheme.
若不考虑量子起伏,合成信号Ea,Eb可经典地表示为其电场状态如图4 所示,显示为椭圆极化状态.
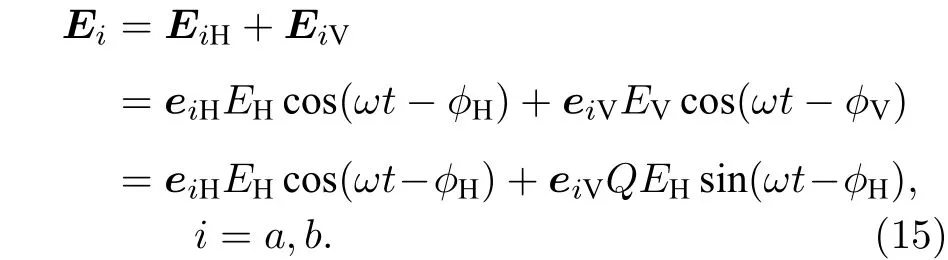
为验证极化纠缠,必须考虑量子起伏,需要使用(10)—(12)式进行判断. 对于与的测量直接使用平衡零差探测装置即可,而对于与则需要在极化栅(polarization grid)前加入法拉第旋转器(Faraday rotator)进行基变换,使得
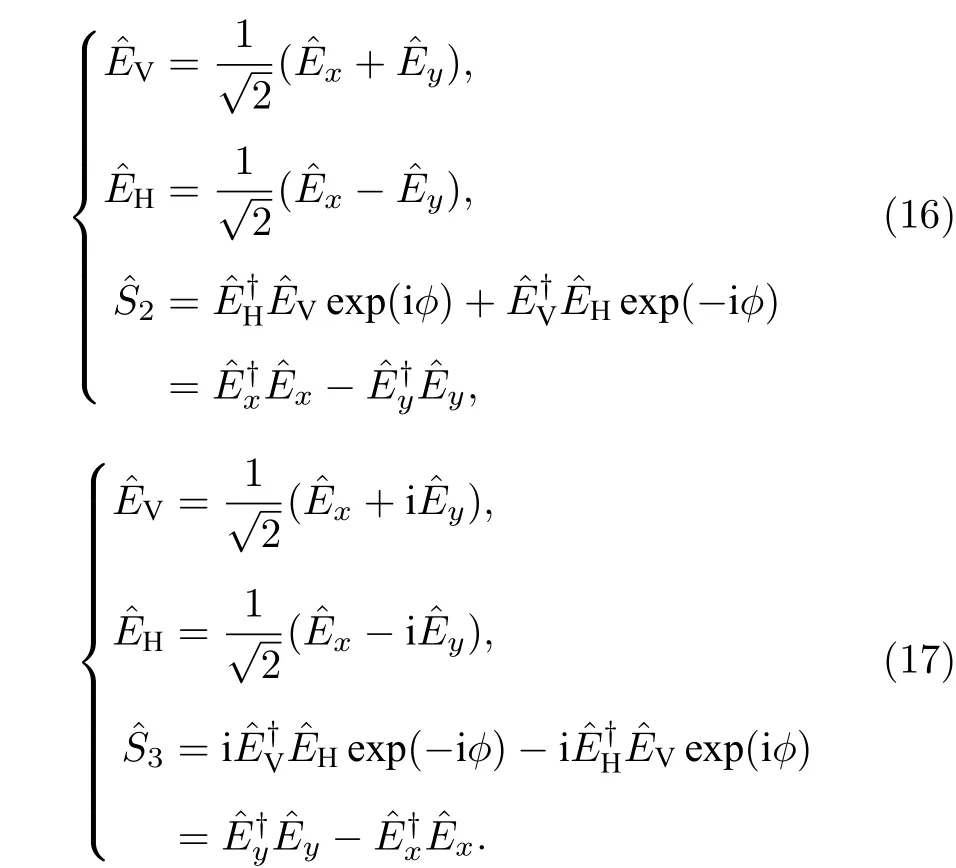
这样,,信号各自的所有斯托克斯参量便可全部测出. 将两套平衡零拍探测装置的输出电流再进行加减,就可以得到±(其中i=0,1,2,3 ).进一步地,利用频谱分析仪获取 ∆2() (其中i=1,2,3 ),得到相应的不可分度,从而判断二组分纠缠的存在与否. 由于(14)式所选择的条件,相位差使得(11)式无法判断,故只能判断与之间、与之间是否存在二组分纠缠.
根据表1 及(14)式,可得,间各斯托克斯参量的起伏如图5 所示.

图3 ,的正交分量间的时域关联 (a)振幅分量XH; (b)相位分量YHFig. 3. Quadrature components correlations ofandin time domain: (a) Amplitude componentXH; (b) phase componentYH.
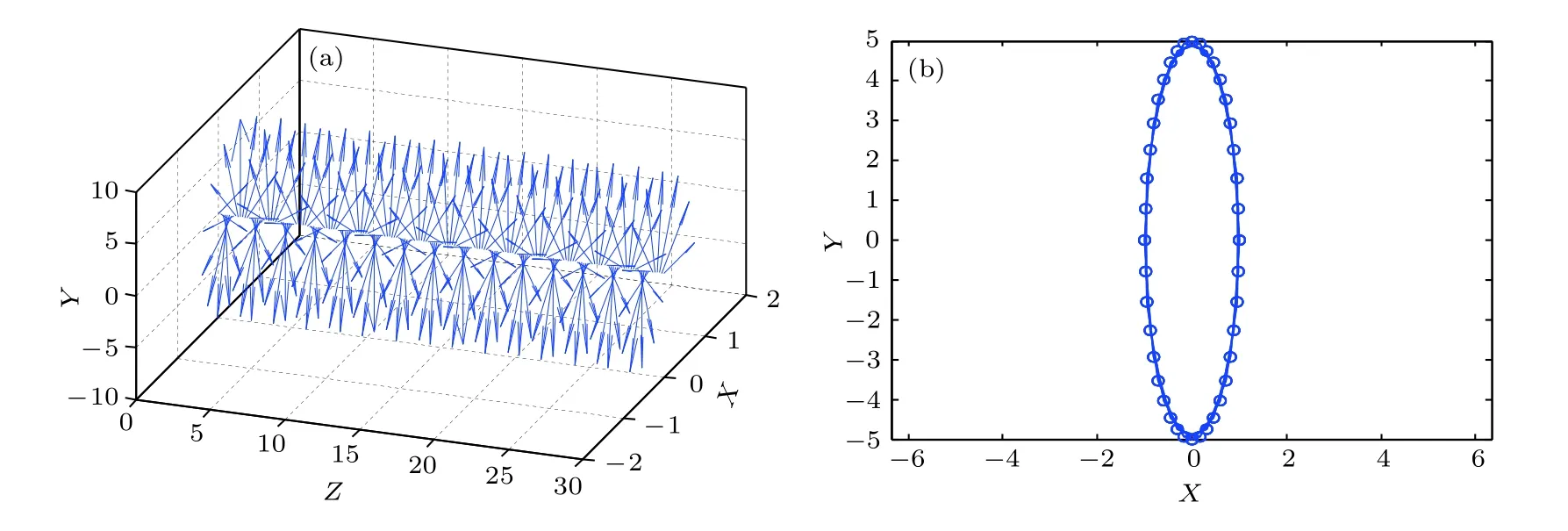
图4 合成信号传输过程电场状态(a)和矢端轨迹(b)Fig. 4. Electric field state (a) and vector end trajectory (b) of combined signal in transmission.

图5 ,对应斯托克斯参量的起伏关系Fig. 5. Fluctuations correlation of corresponding Stokes vectors betweenand.
从图5 可以看出,各分量在低频处均有较高噪声,这是由弛豫振荡噪声[21]引起的,而两信号中的和参量起伏基本一致,均在50 MHz 以上,趋于散粒噪声极限,和参量的起伏则在整个工作带宽范围内均高于散粒噪声极限. 事实上,在表1及(14)式所设条件下,(6)式可进一步化简为

进一步将(10)和(12)式展开分析:
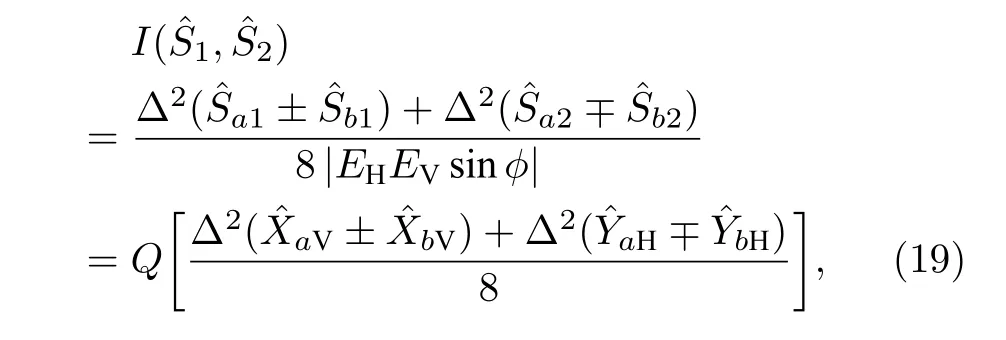
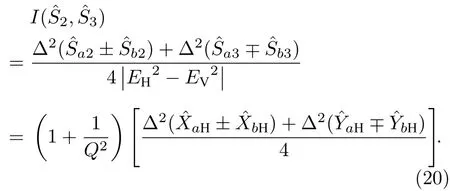
由图6 可知,随着r的增大,有略微减小,在整个工作带宽范围内均保持大于1,说明r的变化对影响不大,这是由于r只影响水平极化分量中的正交分量,而中占主导地位的分量是来自强相干态的垂直分量,因此来自水平极化分量的正交相位起伏对的影响有限. 对于其随着r的增大而减小,且变化幅度较大,在整个工作带宽范围内均小于1,说明受r影响较大. 同时可以发现,对于不同的曲线均在70 MHz 附近,趋于极小值0.25,说明该处的纠缠程度最佳.
另一方面,当r= 2 时,给出I与Q的关系,如图7 所示. 从图7 可以看出,Q越大的值越大,的值越小,且随Q变化幅度 较 大,随Q变 化 幅 度 很 小,这 可 由(20)式给出解释,即当Q值较大时将趋向一定值,从而几乎不再受Q的影响. 在整个JM 工作带宽内,始终大于1,而则始终小于1,且也在70 MHz 附近取得最小值0.25,该点处纠缠程度最佳.
参数Q体现的是垂直极化分量的强相干态信号对于最终输出的涨落的影响,参数r体现的是水平极化信号对于最终输出的涨落的影响,不可分度的大小取决于各信号涨落的大小对Q值变化敏感,而对r值变化敏感,这说明强相干态信号的涨落在纠缠转换中主要投影到了斯托克斯参量中的和上,而正交分量纠缠信号的涨落则主要投影到了斯托克斯参量中的和上,并相应地主导了的值.
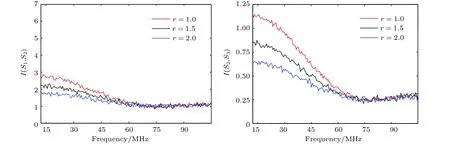
图6 不可分度I与压缩度r的关系Fig. 6. Relations of inseparabilityIand squeezing degree
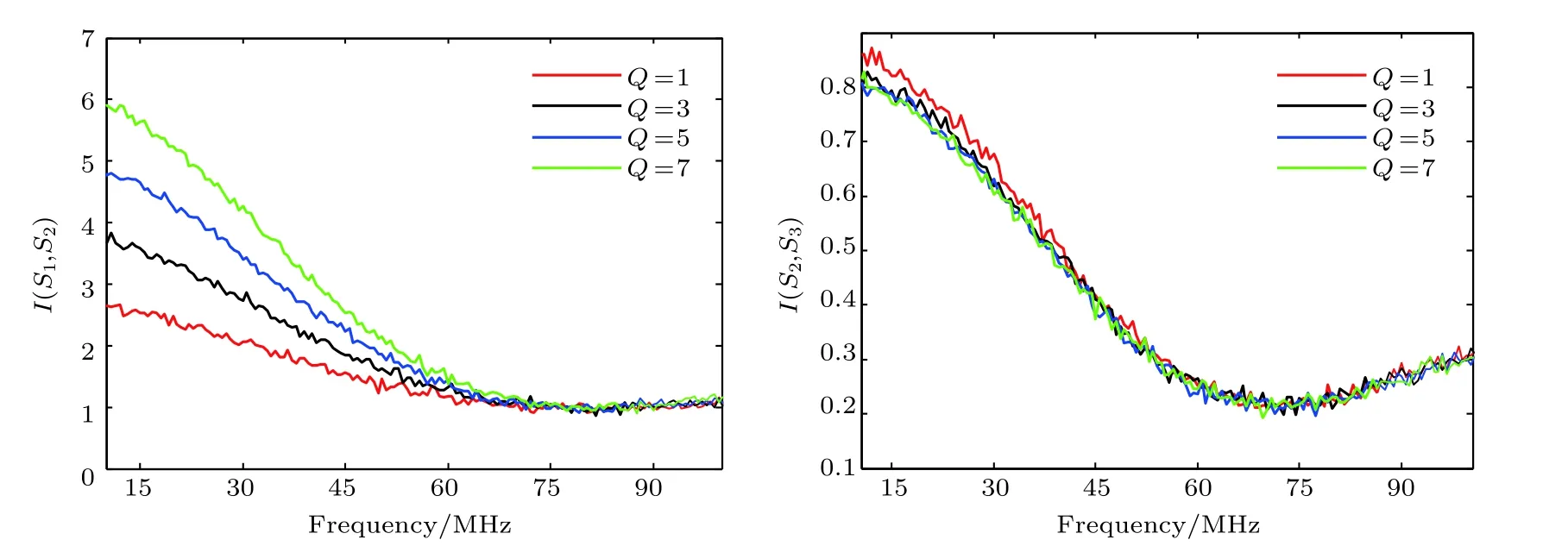
图7 不可分度I与振幅比值Q的关系Fig. 7. Relations of inseparabilityIand amplitude ratioQ:
4 结 论
对连续变量极化纠缠原理进行了阐述,提出了微波二组分极化纠缠的方案,着重对正交分量纠缠到极化纠缠的转换进行了分析,在设定的方案条件下,获得了水平极化分量的正交振幅、相位的时域关联,同时得出了在整个JM 工作带宽内的不可分度详细分析了不可分度I分别与压缩度r、振幅比值Q的关系,发现对Q值变化敏感,而对r值变化敏感,始终大于1、始终小于1,斯托克斯参量和构成不可分态,方案产生的两个微波信号和存在二组分极化纠缠.
附录A 段氏不可分判据的拓展
推导量子态可分条件,对其违反即为不可分,从而可得不可分判据. 最初的段氏判据是从信号的正交分量入手的.

推导,νˆ方差,以下使用 δO和 ∆2O分别代表任意物理观测量O的标准差和均方差:

根据平方和式可知

列出不确定性关系有

则根据不确定性关系可得
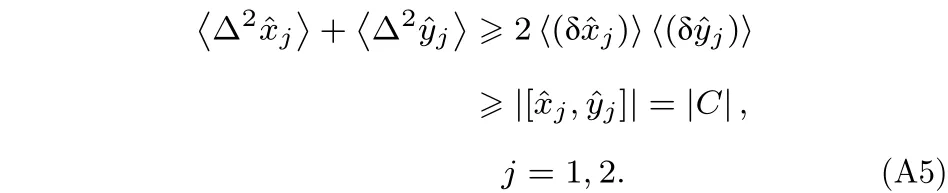
正交分量和满足对易关系:
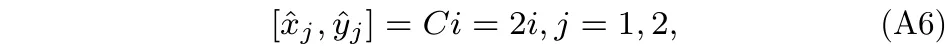
故(A2)式可化为
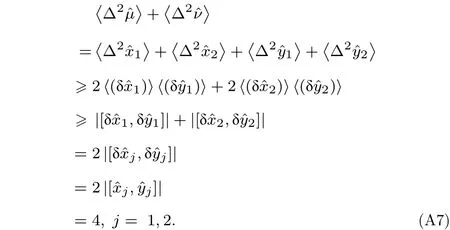
该情况下量子态可分,当(A7)式被违反时则不可分,故段氏不可分判据即为
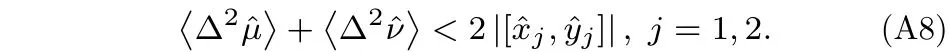
具体针对正交分量而言时,C的值为2,则可以得到

此即为正文中(7)式的推导过程,附录A 只对正交振幅和、正交相位差两观测量进行了举例推导,但该判据对于正交振幅差、正交相位和观测量同样成立.
根据(A7)和(A8)式可对段氏判据进行拓展,对于任意一对厄米量M和N,对于两信号和则有不可分判据如正文中(8)式所示:

以上即为段氏不可分判据的拓展.
