Kiselev 黑洞的热力学性质和物质吸积特性*
2019-04-10魏益焕
魏益焕
(渤海大学数理学院物理系,锦州 121000)
(2018 年11 月19 日收到; 2019 年1 月2 日收到修改稿)
本文考虑带有黑洞视界和宇宙视界的Kiselev 时空. 研究以黑洞视界和宇宙视界为边界的系统的热力学性质. 统一地给出了两个系统的热力学第一定律; 在黑洞视界半径远小于宇宙视界半径的情况下,近似地计算了通过宇宙视界和黑洞视界的热能. 然后,探讨Kiselev 时空的物质吸积特性. 在吸积能量密度正比于背景能量密度的条件下给出黑洞的吸积率,讨论了黑洞吸积率与暗能量态方程参数的关系.
1 引 言
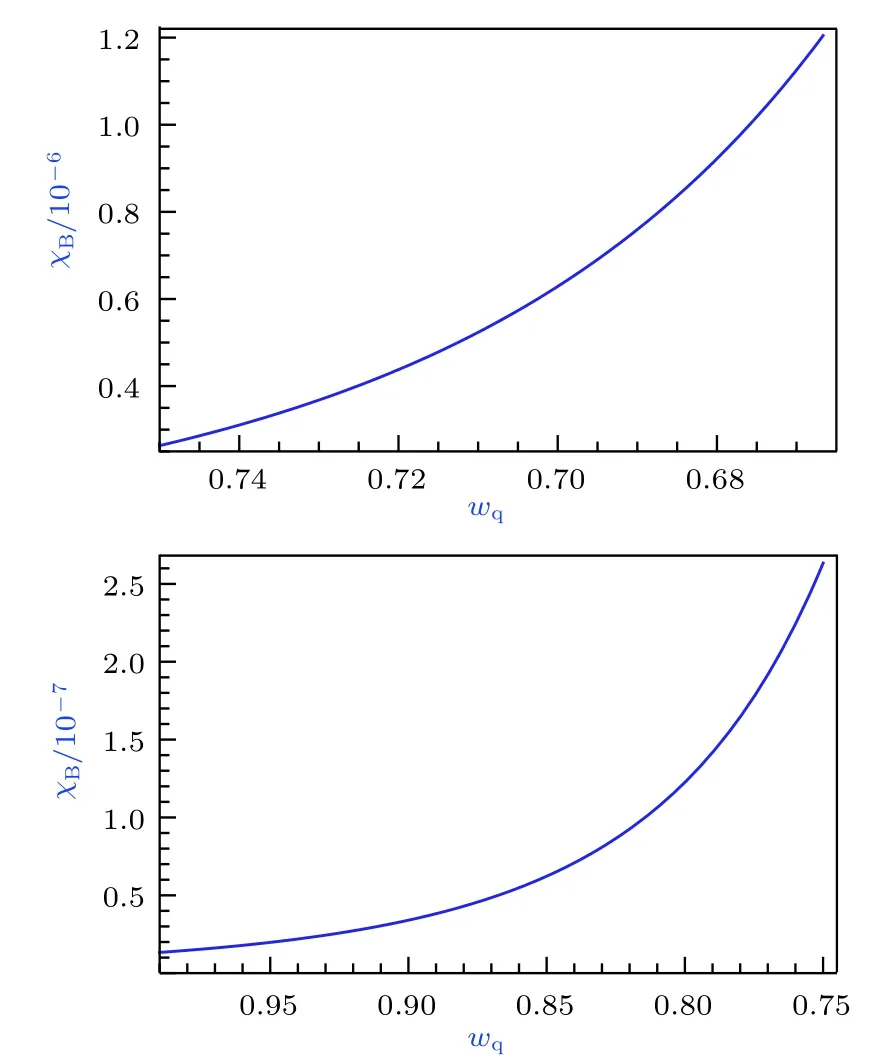
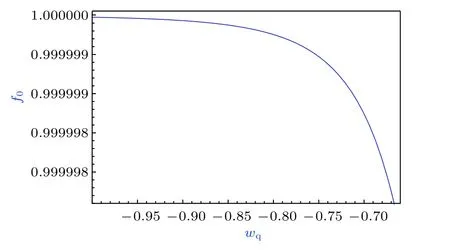
天文观测表明现在的宇宙正加速膨胀[1−3]. 在爱因斯坦引力中,宇宙的加速膨胀被解释为宇宙中暗能量的推动. 暗能量可能是Quintessence 能量(Q 暗能量),也可能是其他形式的能量,如真空能等. 所谓的Q 暗能量指宇宙中的正则标量场,它的态方程参数满足−1 粒子被引力场加速,最终会被天体捕获,此即所谓的天体吸积现象[7,8]. 对于史瓦西黑洞,其吸积性质类似于牛顿理论中孤立球对称天体的吸积性质[9]. 黑洞的稳态吸积问题已经得到了广泛的研究[10−23]. 在wq=−2/3 的情况下,文献[24]研究了Kiselev 黑洞吸积多方流体的问题. 结果显示,多方流体的吸积速率和吸积临界点都与Q 暗能量的能量标度有关. 在文献[24]中,Kiselev 黑洞被考虑为带有两个黑洞视界的黑洞. 对于黑洞周围存在暗能量的情况,Kiselev 时空存在宇宙视界. 本文研究Kiselev 时空中以黑洞视界和宇宙视界为边界的时空区域的热力学性质,探讨Kiselev 黑洞对无压流体物质的吸积特性. 对于时空中存在Q 暗能量的情况,Kiselev 时空度规取下面的形式[4]: 其中λ是具有宇宙尺度的参数,M≪ λ是黑洞的质量. 该时空有一个黑洞视界(半径rB)和宇宙视界(半径rC),其视界半径近似地为 在上面的计算中,已经使用了条件M≪λ. 恒星级质量的黑洞显然满足这个条件,即便是超大质量的星系级黑洞,这一条件也成立. 对于宇宙视界,(5)式右边的第一项是小量,宇宙视界温度近似为由度规函数f=0 ,得到Kiselev 时空(黑洞)的质量即 其中 (7)式中符号“+”和“–”分别对应到黑洞视界和宇宙视界的情况. 对(6)式两边微分得到微分形式的斯马尔关系 在Kiselev 黑洞斯马尔关系的表示中,既可采用定义在黑洞视界上的热力学量,也可采用定义在宇宙视界上的热力学量. (9)式给出了Kiselev时空的质量增加量与视界熵增加量和参量λ增加量的关系. 球对称时空(1)中半径为r的球面内的爱因斯坦准局域能为[25] 将度规函数(2)式代入(10)式给出Kiselev 时空中半径为r的球面内的能量 宇宙视界附近的能量密度大致正比于Q 能态方程参数的大小,因此具有相同的量级,但黑洞视界附近的能量密度却随wq增大而迅速增加(表1). 将r=rB,C代入(10)式得到黑洞视界和宇宙视界内的能量容易验证,由黑洞视界和宇宙视界包围的系统满足热力学第一定律 其中dQB和 dQC分别是流入黑洞和宇宙视界内的热量,dwB和dwC分别是时空中的流体对黑洞视界和宇宙视界的功,pB,C=pr(rB,C)和考虑到pB,C=−ρB,C,Kiselev 时空中流体对黑洞视界和宇宙视界的功可写为 在视界发生微小改变的过程中,时空中流体对视界的功等于视界所掠过时空区域的能量∆wB,C=ρB,C∆VB,C(图1). 表1 黑洞视界附近背景时空的能量密度Table 1. Energy density of spacetime near the horizon of black hole. 图1 (a)黑洞视界做功示意图; (b)宇宙视界做功示意图;其中BHH 和CH 分别表示黑洞视界和宇宙视界,∆ rB,C 表示黑洞视界和宇宙视界半径的微小变化,虚线表示变化后的黑洞视界和宇宙视界Fig. 1. (a) Doing work of black hole horizon; (b) doing work of cosmic horizon. BHH and CH stand for the black hole horizon and the cosmic horizon,respectively. ∆ rB,C denotes a small change of the radii of black hole horizon and cosmic horizon. The dotted lines represent the changed black hole horizon and the changed cosmic horizon. 在静态球对称时空中,沿径向运动的流体四维速度是利用归一化条件uµuµ=−1 ,得到流体四维速度的第0 分量其中xµ=(t,r,θ,φ) . 其中u=u1. 物质的四维流矢量定义为Jµ=nuµ,其中n是流体的粒子数密度. 四维流守恒律=0给出[24] 其中CJ̸=0 是常数. 对于流向引力中心的流体,有CJ <0. 理想流体的四维能量-动量张量取如下形式: 其中ρm和pm分别代表流体的能量密度和压强. 流体四维能量-动量张量守恒方程的零分量方程为 即 其中C1是常数. 对于pm>−ρm的情况,积分常数C1<0 . 方程uν=0 给出[12]对(21)式积分得到 这里C2<0 是积分常数. 若吸积流体是无压的物质,则(22)和(17)式是同一方程. 由(20)和(22)式得到 对(23)式求导给出 2uu′=−f′,其中f′=df/dr.对于u=0 ,u′=0指f′=0. 方程f′=0 给出Kiselev时空度规函数取极大值的位置r0(图2), 其中u0=u(r0) 为流体的最大速度. (25)式右边的f0是f在黑洞视界和宇宙视界间的最大取值 在r=r0附近,Kiselev 时空几乎是平直时空(图3).在r=r0处,粒子应该有极小速率 (|u0|≪1) . 在这一 假 设 下,有+f0≈f0≈1和C2≈C1=C.在接近黑洞视界处(f≈0 ),流体四维速度的径向分量uB近似地为−1 . 图2 在M=10−2 l.y.和λ=1.378×1010 l.y.条件下的r0-wq曲线Fig. 2. Ther 0-wq curve (M=10−2 l.y. andλ=1.378×1010 l.y.). Kiselev 黑洞对无压理想流体的吸积率为 C=ρmBuBmB=ρm(rB) 其中常数 ,能量密度 . 黑洞视界附近的流体四维速度uµ的径向分量近似为−1 ,常数C仅依赖黑洞视界半径和吸积流体的能量密度. 假定黑洞视界附近被吸积流体的能量密度与背景能量密度成正比ρmB=ηBρB,则黑洞的吸积率为 被吸积流体的能量密度对时空背景的影响是微小的,因此要求比例系数ηB≪1. 对应于wq=−2/3和wq=−1 ,分别有最大吸积率χmax≈1.2×10−6ηB和最小吸积率χmin≈1.2×10−8ηB(图4). 上面的讨论是在假定参数ηB不依赖wq的情况下进行的.假定ηB随wq足够缓慢地改变,则黑洞的吸积率会随wq的增大而增大. 图3 在M=10−2 l.y.和λ=1.378×1010 l.y.条 件下的f0-wq 曲线,对 于和− 1 ,分 别 有f 0 ≈0.999998 和0.99999998Fig. 3. Thef 0-wq curve (M=10−2 l.y. andλ=1.378×1010l.y.). For and− 1 ,the metric functionf0 ≈0.999998 and 0.99999998,respectively. 在M≪ λ的情况下,Kiselev 时空中的流体对宇宙视界所做的功和流入宇宙视界的热量近似地为和在−1 图4 黑洞吸积率χ B (单位η B)与w q的关系图(M=1 0−2 l.y.和λ=1.378×1010 l.y.)Fig. 4. Relationship between black hole accretion rateχB(unitηB) andw q(M=10−2 l.y.andλ=1.378×1010 l.y.). 现在宇宙中约 1 /3 和 2 /3 的部分为物质和暗能量. 宇宙加速膨胀要求宇宙有效态方程参数weff<−1/3. 对于由无压的物质和Q 能构成的宇宙,它指暗能量态方程参数的取值被限制在范围wq<−2/3之内. Kiselev 时空的能量分布明显地依赖它的态方程参数wq. 对于wq=−2/3和wq=−1这两种情况,黑洞视界附近的Q 能密度相差11 个量级. 另一方面,随 Q 能的态方程参数减小,r0的取值增大. 在rB⩽r 2 Kiselev 时空的热力学性质


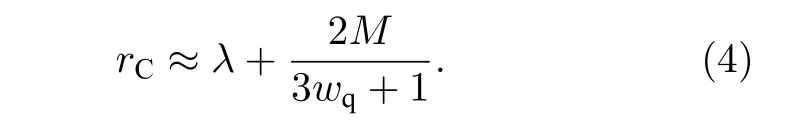
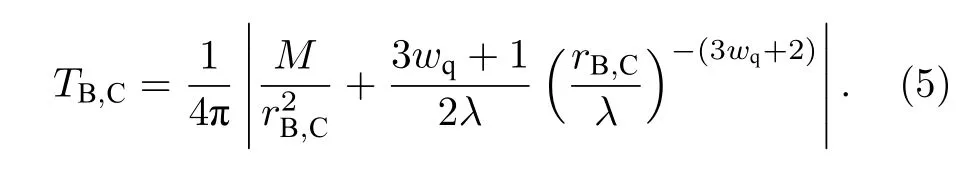

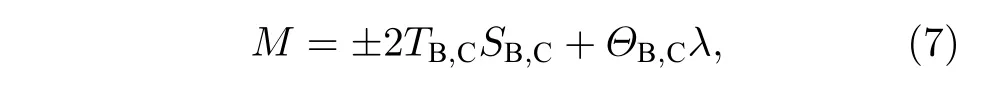

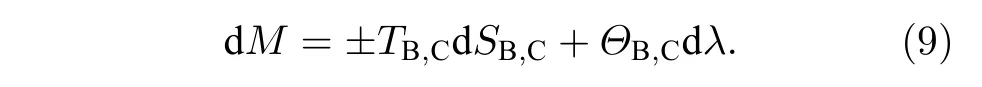


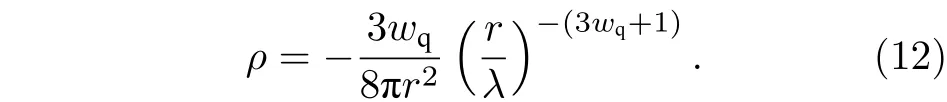
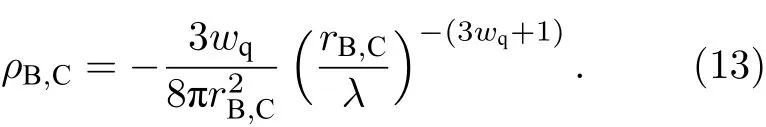




3 Kiselev 时空的物质吸积特性

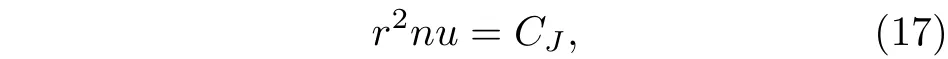


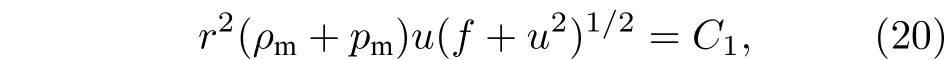
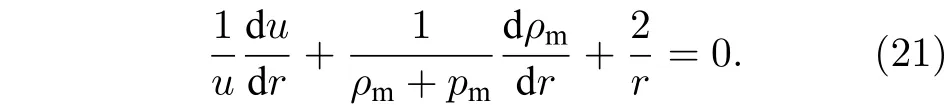
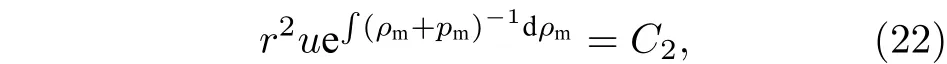

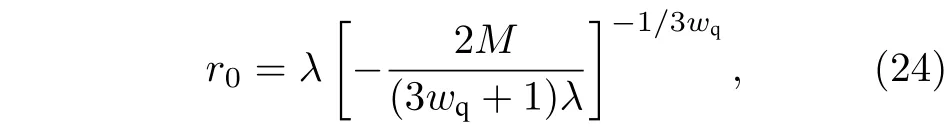

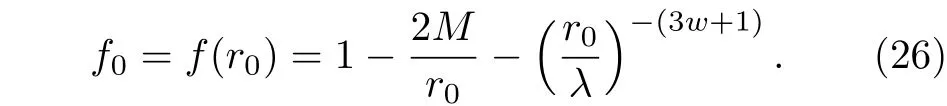


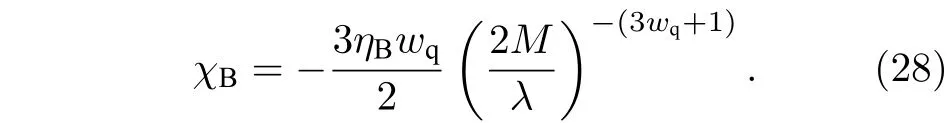
4 结论与讨论