激光冷却SH–阴离子的理论研究*
2019-04-10万明杰李松金成国罗华锋
万明杰 李松 金成国 罗华锋
1) (宜宾学院计算物理四川省高等学校重点实验室,宜宾 644007)
2) (长江大学物理与光电工程学院,荆州 434023)
3) (宜宾学院化学与工程学院,宜宾 644007)
(2018 年11 月16 日收到; 2019 年1 月2 日收到修改稿)
本文采用多组态相互作用及Davidson 修正方法和全电子基组计算了SH–阴离子的 X1Σ+ ,a3Π和A1Π态的势能曲线、电偶极矩和跃迁偶极矩. 计算的光谱常数与实验值及已有的理论值符合得很好. 在计算中考虑了自旋-轨道耦合效应. 计算得到跃迁具有高对角分布的弗兰克-康登因子,分别为0.9990 和0.9999; 计算得到 a3Π1和 A1Π1 态的自发辐射寿命分别为1.472 和0.188 ms.跃迁存在中间态 a3Π0+和 a3Π1 ,但中间态对激光冷却SH–阴离子的影响可以忽略. 分别利用跃迁构建了准闭合的能级系统,冷却所需的激光波长分别为492.27 和478.57 nm. 最后预测了激光冷却SH–阴离子能达到的多普勒温度和反冲温度. 这些结果为进一步实验提供了理论参数.
1 引 言
由于双原子分子结构的复杂性,其激光冷却的研究具有很大的挑战性,近年来一直是原子分子物理和光学等领域的研究热点. 实验上[1−3]和理论上[4−9]针对激光冷却分子或分子阳离子都有大量研究.
然而阴离子的激光冷却研究较少. 研究表明一些氢化物阴离子是激光冷却的候选离子. 杨传路课题组提出了激光冷却NH–[10]和BH–[11]阴离子的方案. 在设计激光冷却方案时,两种阴离子都构建了12Σ+↔12Π 准闭合能级系统. 计算得到了NH–和BH–阴离子的弗兰克-康登因子分别为0.999 和0.942,以及 12Σ+态的自发辐射寿命分别50.4 和91.8 ns. 最近本课题组[12]在考虑自旋-轨道耦合(SOC) 效应时对激光冷却OH–阴离子的可能性进行了研究. 分别利用跃迁构建了准闭合能级,并给出了冷却OH–阴离子的方案. SH–和OH–具有类似的结构,本文研究激光冷却SH–阴离子的可能性.
实验上,Steiner[13]于1968 年首次报道了SH–阴离子基态 X1Σ+的光谱常数. 1981 年,Breyer 等[14]观测到了一系列阴离子的高分辨率光电子能谱. 得到了OH–,SH–和SD–阴离子的光谱常数,其中转动常数为B0(OH–) =(18.75±0.15) cm–1,B0(SH–) =(9.39±0.30) cm–1,B0(SD–) =(4.87±0.20) cm–1.同年,Janousek 和Brauman[15]在SH–阴离子的光致分离频谱中观测到了转动结构,并得到了SH 分子的亲合能为(2.314±0.003) eV. 理论上,1967 年,Cade[16]通过求解Hartree-Fock-Roothaan 矩阵方程研究了 SH–阴离子的势能曲线. 1978 年,Rosmus和Meyer[17]采用赝势轨道组态相互作用和耦合电子对近似(CEPA)方法计算了第一行和第二行双原子氢化物阴离子基态的势能曲线,并拟合得到了光谱常数. 1985 年,Senekowitsch 等[18]采用 CEPA方法计算了SH–阴离子的势能曲线和偶极矩函数,在平衡核间距Re处的偶极矩为0.27 Debye (D).2016 年,Vamhindi 和 Nsangou[19]采用包含 Davidson 修正的多参考组态相互作用(MRCI+Q)方法[20−22]计算了 SH–阴离子 X1Σ+,a3Π和A1Π 态的势能函数. 拟合得到了其光谱常数Re( X1Σ+) =1.344 Å,Re( a3Π) =1.3746 Å,Re( A1Π ) =1.3432 Å,但他们没有计算激发态到基态跃迁的弗兰克-康登因子和自发辐射速率以及激发态的自发辐射寿命.
本文在考虑SOC 效应下分析SH–阴离子的光谱常数和跃迁性质,构建准闭合的能级系统进行激光冷却SH–阴离子,给出冷却途径.
2 计算方法
采用MRCI+Q方法计算SH–阴离子 X1Σ+,a3Π ,A1Π ,13Σ+和 21Σ+态的电子结构. 以完全活性空间自洽场方法(CASSCF)[23,24]所产生的波函数为基础构造了CI 波函数,进行MRCI+Q的计算. 同时在计算中通过三阶Douglas-Kroll 哈密顿量 (DKH3)[25,26]考虑了标量相对论修正,通过Breit-Pauli 算符[27]考虑了 SOC 效应. 所有计算都是由 MOLPRO 2010 程序[28]得到.
在CASSCF 计算中,选取6 个分子轨道作为活性轨道,包含 H 的 1s 和 S 的 3s3p4s 轨道,8 个电子占据 (4,1,1,0)活性空间,可以写为 CAS(8,6),而 S 的 1s2s2p 轨道为双占据的闭壳层轨道;在MRCI+Q计算中考虑了核-价电子(CV)关联效应,S 的 1s2s2p 轨道参与 CV 关联计算. 在 Λ -S 和 Ω 的计算中,对 S 原子选取了 ACV5Z-DK 全电子基组[29],对H 原子选取了AV5Z-DK 全电子基组[30].
本文采用Murrell-Sorbie 解析势能函数[31]来拟合 SH–阴离子 Λ-S 和 Ω 态的光谱常数. 同时使用均方根值 (RMS)来评估拟合效果. 弗兰克-康登因子(fν′ν′′) 、自发辐射速率(Aν′ν′′)和自发辐射寿命(τ)均采用LEVEL8.0 程序[32]计算.
3 结果与讨论
3.1 势能曲线与光谱常数
本文在MRCI+Q水平下计算了SH–阴离子的
X1Σ+,a3Π ,A1Π ,13Σ+和 21Σ+电子态的势能曲线,结果如图1 所示. 从图1 可以看出,在计算的5 个态中 21Σ+态为最高态,说明 21Σ+态在激光冷却SH–阴离子过程中不是中间态. 13Σ+态为排斥态. X1Σ+,a3Π ,A1Π和 13Σ+态对应于最低离解通道 S–(2Pu) + H(2Sg),21Σ+态则对应于第三离解通道 S(1Dg) + H–(1Sg). 计算的两通道之间的能量差为 19825.64 cm–1. H 和 S 原子的亲和能的实验值分别为 6082.99 cm–1[33]和 16752.83 cm–1[34],而S 原子基态3Pg与第一激发态1Dg的能量差为9239.0 cm–1[35],可以计算出两通道之间的能量差的实验值为 19908.84 cm–1. 本文的计算值与实验值符合得很好,仅有0.42%的误差.
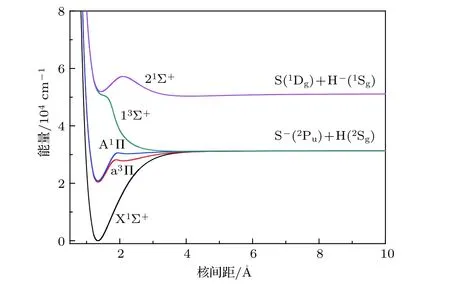
图1 SH–阴离子的 X1Σ+,a3Π ,A1Π ,13Σ+ 和 21Σ+ 态的势能曲线Fig. 1. Potential energy curves for the X1Σ+ ,a3Π ,A1Π ,and 21Σ+ states of SH– anion.
计算所得 X1Σ+,a3Π和 A1Π 态的光谱常数如表1所列 . SH–基 态 X1Σ+的平衡核间距Re为1.3435 Å,与实验值[13]相差 0.0035 Å,误差仅为0.26%; 谐振频率ωe和转动常数Be分别为2622.04和 9.5590 cm–1,与最新实验值[14]的误差分别为0.98%和1.80%. 基态的非谐振频率ωeχe和势阱深度De的结果与Rosmus 和Meyer[17]报道的理论结果更接近. 可以看出基态的计算结果与实验值及其他理论值符合得很好. 和以往的研究结果不同,a3Π 和 A1Π 态具有双势阱结构,两个态分别在约1.89 和1.95 Å发生预解离. a3Π和 A1Π 态第一势阱的平衡核间距Re与Vamhindi 和Nsangou[19]报道的理论值符合很好,误差分别为2.04%和0.07%. 本文得到了 a3Π和 A1Π 态的两个势阱的谐振频率ωe、非谐振频率ωeχe和势阱深度De,结果列于表1 中.
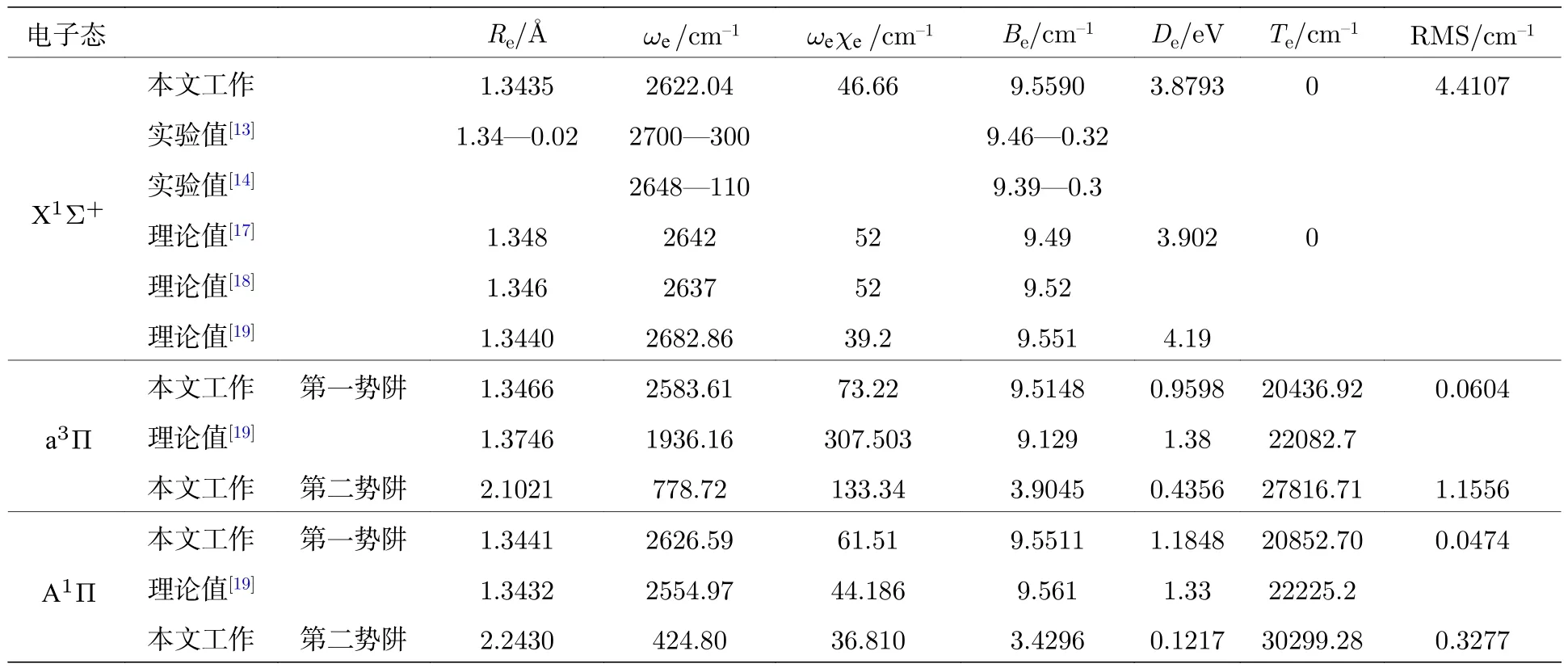
表1 SH–阴离子的Λ-S 态的光谱常数Table 1. Spectroscopic parameters for the Λ -S states of SH– anion.
考虑SOC 效 应 后,a3Π态 分 裂 成4 个 Ω 态( a3Π2,a3Π1,a3Π0−,a3Π0+),S(2P)原子态分裂为S(2P3/2)和S(2P1/2). 其 Ω 态的势能曲线如图2 所示. X1Σ+0+,a3Π2,a3Π1,a3Π0−和 A1Π1态具有相同的离解极限S–(2P3/2) + H(2S1/2); a3Π0+,b3和态具有另一个离解极限S–(2P1/2) + H(2S1/2).预测出S–负离子2P 原子态的分裂值为505.79 cm–1.

图2 SH–阴离子的 Ω 态的势能曲线Fig. 2. Potential energy curves for the Ω states of SH– anion.
本文首次报道了SH–阴离子 Ω 态的光谱常数,如表2 所列. 可以看出SOC 效应对不分裂的X1Σ+和 A1Π 态的光谱常数影响很小. 此结果和OH–阴离子[12]类似. 也得到了 a3Π 态的分裂常数ASO:ASO( a3Π1–a3Π2) =116.06 cm–1,ASO( a3Π0−–a3Π1) =261.24 cm–1以及ASO( a3Π0+–a3Π0−) =0.13 cm–1. 而OH–阴离子[12]:ASO( a3Π1–a3Π2) =58.41 cm–1和ASO( a3Π0–a3Π1) =78.21 cm–1. 对比两个离子 a3Π 态的分裂值可以看出,SOC 效应对SH–阴离子的影响要更大.
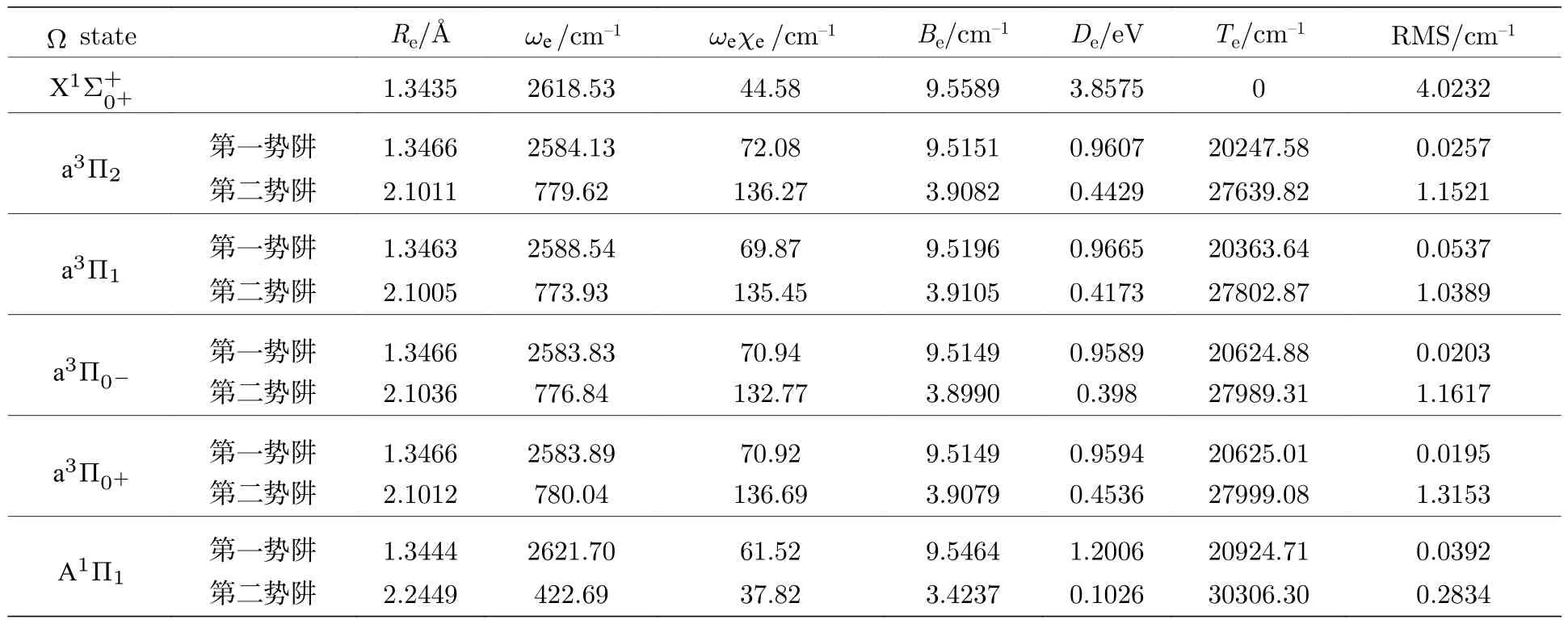
表2 SH–阴离子的 Ω 态的光谱常数Table 2. Spectroscopic parameters for the Ω states of SH– anion.
为了评估 Λ -S 和Ω 态的势能曲线的拟合质量,本文给出RMS 值,列在表1 和表2 中. 最大RMS 值仅为4.4107 cm–1. 可以看出本文的计算结果是可靠的.
3.2 跃迁偶极矩
当考虑SOC 效应后,根据跃迁选择定则可知,a3Π2↔X1和 a3Π0− ↔X1跃迁不被允许. 本文计算了 A1Π1↔X1,a3Π0+↔X1,a3Π1↔X1Σ+0+,A1Π1↔a3Π0+和 A1Π1↔a3Π1跃迁的跃迁偶极矩,结果如图3 所示.
计算的5 种跃迁中 A1Π1↔X1跃迁的强度最大,在平衡核间距处的跃迁偶极矩为–1.3636 D.值得注意的是 a3Π1↔X1跃迁在平衡核间距处的跃迁偶极矩为0.5269 D,比之前得到的OH–阴离子的值[12]更大. 另一方面SH–阴离子 a3Π1的垂直跃迁能为20363.64 cm–1,比OH–阴离子 a3Π1的垂直跃迁能18664.98 cm–1[12]大. 由此说明SH–阴离子 a3Π1↔X1跃迁的爱因斯坦辐射速率比OH–阴离子大. 在构建激光冷却SH–阴离子的方案时必须考虑 a3Π1↔X1跃迁. 值得注意的是a3Π0+↔X1,A1Π1↔a3Π0+和 A1Π1↔a3Π1跃迁的跃迁偶极矩在平衡核间距处接近零,说明这3 种跃迁的强度很低.
3.3 SH–阴离子的激光冷却
分子离子的辐射速率(Aν′ν′′)、弗兰克-康登因子(fν′ν′′)和辐射寿命(τ)决定了此体系是否适合激光冷却. 根据跃迁规则可知,考虑SOC 效应后只有 a3Π1↔X1和 a3Π0+↔X1跃迁被允许.本文采用LEVEL8.0 程序计算 A1Π1↔X1,a3Π0+↔X1,a3Π1↔X1跃 迁 的Aν′ν′′和fν′ν′′,并得到了 a3Π1,A1Π1和 a3Π0+态的辐射寿命,所有数据如表3 所列.
3.3.1 自旋阻禁跃迁的激光冷却
首先讨论构建 a3Π1↔X1准闭合能级进行激光冷却SH–阴离子的可能性. 从表3 可以看出,a3Π1↔X1跃迁具有高对角分布的fν′ν′′,即f00=0.9990. 且f00,f01,f02之和基本等于1,可以保证此循环的准闭合. 除了具有高对角分布的fν′ν′′,激光冷却离子还需要具备很强的循环速率(105—108s–1)和短的自发辐射寿命,从表3 可以看到a3Π1↔X1跃迁的总自发辐射速率A0=6.79 ×105s–1,即自发辐射寿命为1.472 μs . 此结果约为OH–阴离子 a3Π1↔X1跃迁的总自发辐射速率的7 倍[12]. 相比于OH–阴离子,激光冷却SH–阴离子所需的时间更短. 和GaF 分子类似[8],由于其f00足够大,只需要一束主激光来驱动a3Π1↔X1跃迁,所需的激光波长λ00=492.27 nm. 由此构建了 a3Π1↔X1自旋阻禁跃迁对SH–阴离子进行激光冷却,冷却方案如图4 所示.
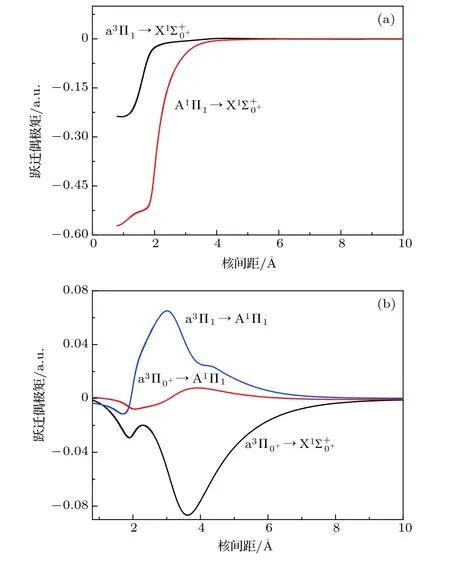
图3 SH–阴离子的跃迁偶极矩 (a) A1Π1 ↔X1和a3Π1 ↔X1跃迁; (b) a3Π0+ ↔X1 ,A1Π1 ↔a3Π0+和 A1Π1 ↔a3Π1 跃迁Fig. 3. Transition dipole moments of SH– anion: (a) The A1Π1 ↔X1and a3Π1 ↔X1Σ+0+ transitions; (b) the a3Π0+ ↔X1 ,A1Π1 ↔a3Π0+ andA1Π1 ↔a3Π1 transitions.
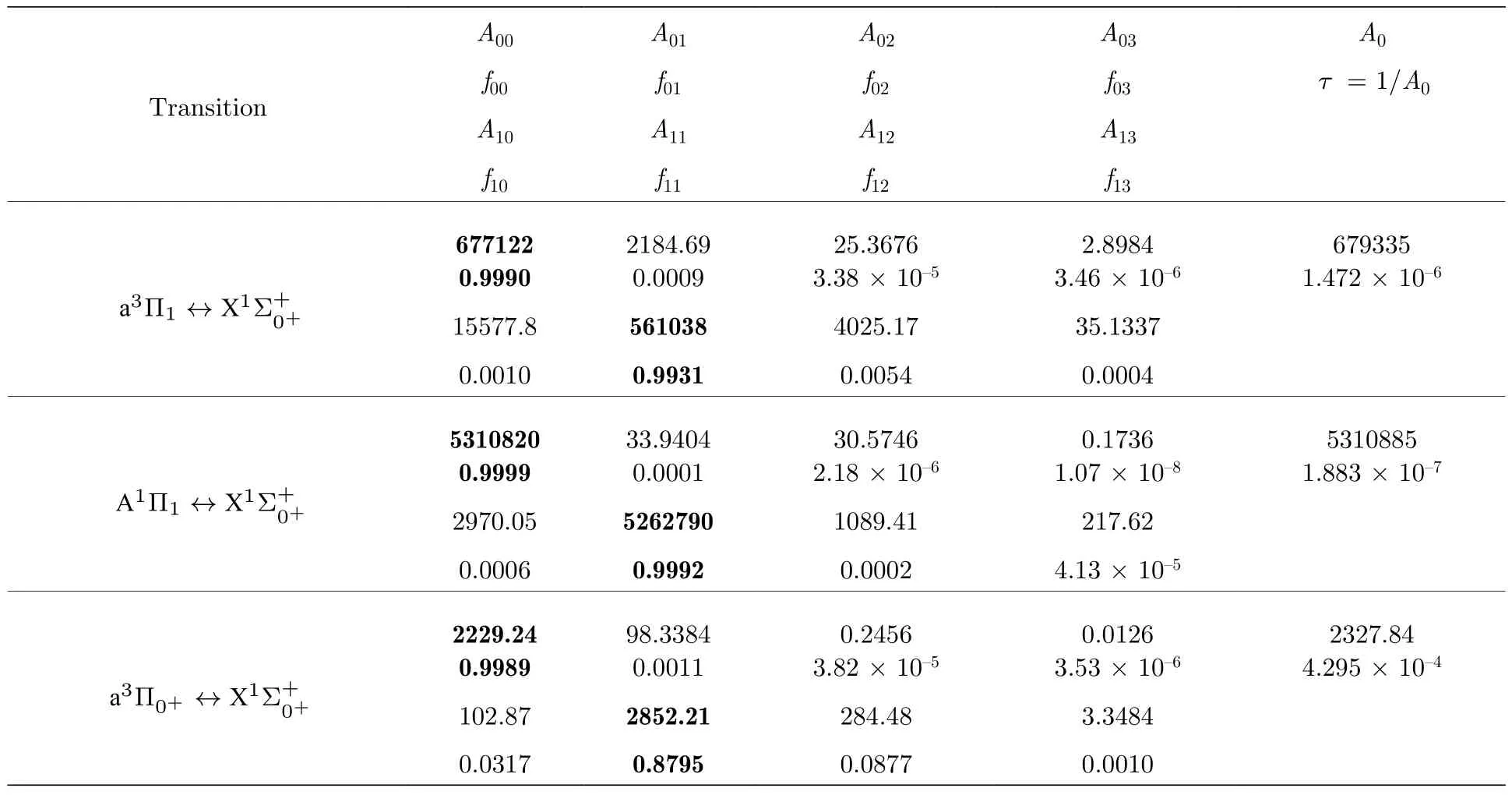
表3 SH–阴离子的辐射速率(单位为s–1)、弗兰克-康登因子和自发辐射寿命(单位为s)Table 3. Emission ratesA ν′ν′′(unit of s–1),Franck-Condon factorsf ν′ν′′and spontaneous radiative lifetimesτ(unit of s)of SH– anion.
对于 a3Π0+↔X1跃迁,虽然具有非常高的对角分布弗兰克-康登因子(f00=0.9989),能满足跃迁循环的准闭合,但总自发辐射速率A0太小,只有2229.24 s–1,不满足激光冷却分子离子对循环速率的要求.

图4 采用 a3Π1↔X1 跃迁进行激光冷却SH–阴离子的方案,实线为所需激光,虚线为自发辐射的弗兰克-康登因子Fig. 4. Proposed laser cooling scheme for thea3Π1↔X1Σtransition (solid line) and spontaneous decay.
3.3.2 三电子能级的激光冷却
从表3 中可以看出,相比于 a3Π1↔X1跃迁,A1Π1↔X1跃迁具有更高对角分布的弗兰克-康登因子(f00=0.9999)和更大的自发辐射速率(A0=5.31 × 106s–1),A1Π1态的自发辐射寿命τ(ν′=0)=0.188 μs.
在满足前两个条件的同时必须要考虑中间态a3Π1和 a3Π0+的存在对 A1Π1↔X1能级准闭合性的影响,可以通过振动分支损失比来分析其影响. 振动分支损失比可以表示为:η1=γ1/γΣ或η2=γ2/γΣ,其中γ1,γ2和γΣ分别表示 A1Π1↔a3Π1,A1Π1↔a3Π0+和 A1Π1↔X1跃迁的总自发辐射速率. A1Π1↔a3Π1和 A1Π1↔a3Π0+在弗兰克-康登区域的跃迁偶极矩接近零. 计算得到这两种跃迁的总自发辐射速率分别只有1.85 × 10–2和7.24 ×10–3s–1. 而 A1Π1↔X1跃迁的总自发辐射速率为5.31 × 106s–1. 得 到η1<5×10−9和η2<2×10−9.η值远小于YO 分子的实验值(4.0 × 10–3)[3],说明中间态 a3Π1和 a3Π0+的存在对激光冷却的影响可以忽略不计.
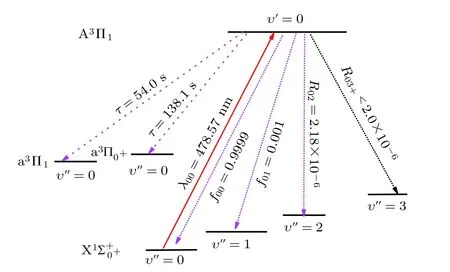
图5 采用 A1Π1 ↔X1 跃迁进行激光冷却SH–阴离子的方案,其中实线为所需激光,虚线为自发辐射的弗兰克-康登因子Fig. 5. Proposed laser cooling scheme for theA1Π1 ↔X1 transition (solid line) and spontaneous decay.
由于f00足够大,只需要一束主激光来驱动A1Π1↔X1跃 迁,其 波 长λ00=478.57 nm.由此构建了三电子能级跃迁对SH–阴离子进行激光冷却,冷却方案如图5 所示.
3.3.3 多普勒温度和反冲温度
多普勒温度的计算公式为TDoppler=h/4kBπτ[36],其中h为普朗克常数,kB为玻尔兹曼常数,τ为激发态的自发辐射寿命. 经计算,采用a3Π1↔X1和 A1Π1↔X1跃迁进行激光冷却SH–阴离子的多普勒温度分别为2.6 和20.28 μ K .
而反冲温度计算公式为Trecoil=h2/mkBλ2[37],其中λ为激光冷却离子的主激光波长. 采用a3Π1↔X1和 A1Π1↔X1跃迁进行激光冷却SH–阴离子的反冲温度分别为2.43 和2.56 μ K .
由于考虑了单光子反冲,可以看出理论上通过两种方案激光冷却SH–阴离子所能达到的反冲温度都低于多普勒温度.
4 结 论
采用MRCI+Q计算了SH–阴离子 X1Σ+,a3Π和 A1Π 态的电子结构,在计算过程中考虑了DKH3 标量相对论修正和CV 关联效应. 在MRCI+Q水平下考虑SOC 效应计算了 Ω 态的势能曲线和跃迁偶极矩. 得到的光谱常数与已有实验值和理论值符合得很好. 本文第一次报道了 Ω 态的光谱常数和跃迁性质. 计算发现 a3Π1↔X1跃迁的跃迁偶极矩很大,在平衡核间距处为0.5269 D.
使用LEVEL8.0 程序计算了SH–阴离子a3Π1↔X1和 A1Π1↔X1跃迁的弗兰克-康登因子、辐射速率和辐射寿命. 计算结果表明,a3Π1↔X1和 A1Π1↔X1跃迁都具有非常高的对角分布弗兰克-康登因子,分别为0.9990 和0.9999,同时具有大的自发辐射速率,分别为6.79 ×105和5.31 × 106s–1. 对于 A1Π1↔X1跃迁存在中间态 a3Π1和 a3Π0+,但其振动分支损失比非常小,可以忽略中间态的存在对循环跃迁的影响,说明可以通过两种跃迁方式来对SH–阴离子进行激光冷却. 本文分别制定了自旋阻禁跃迁和三电子能级跃迁进行激光冷却SH–阴离子的方案,最后预测了两种方案进行激光冷却SH–阴离子的多普勒温度和反冲温度.
