系统风险不同预期下的存款保险费率测算
2019-04-09吕筱宁
吕筱宁
(东北财经大学 金融学院,辽宁 大连 116024)
0 引言
经国务院第67次常务会议通过,自2015年5月1日起,在我国境内设立的商业银行、农村合作银行等吸收存款的银行业金融机构(以下统称银行),应当依照《存款保险条例》投保存款保险。自此,酝酿多年的存款保险制度在我国开始施行。费率的厘定机制是存款保险制度的核心,当前我国存款保险费率由基准费率和风险差别费率构成[1]。基准费率标准依据经济金融发展状况、存款保险基金的累积水平等因素制定,而差别费率水平主要反映各银行存款面临的不同风险状况。
从费率构成来看,我国存款保险费率机制在兼顾经济发展形势和基金充足性问题的基础上,采用了差别费率制。目前越来越多的国家和地区实施风险差别费率的存款保险制度,但多数差别费率定价方法仅关注单个银行的破产风险,忽略了银行业作为一个整体面临的系统性风险问题,因此相应的费率厘定方法可能存在费率低估现象[2]。Pennacchi[3]研究表明,与其他保险不同,仅根据单个银行风险水平确定的存款保险费率不足以补偿银行面临的系统性风险,因此公平的存款保险费率在考虑单个银行违约成本的基础上应有所加成。Acharya等[4]指出合理的存款保险费率应涵盖多种成本,包括银行破产成本[5]以及应对极端事件的风险准备金成本。部分学者在关注费率低估现象的基础上,给出了改进的费率厘定方法。Hwang等[6]从银行破产外部效应的角度进行了费率加成,利用期权定价模型计算了存款保险费率的封闭解。Staum[7]考虑了银行资产流动性对其他银行破产损失的影响,进而给出了考虑资产流动性影响的存款保险定价模型。但现有费率加成模型的关注点,与我国存款保险制度运行初期的风险因素并不十分契合。
目前存款保险制度在我国刚刚推行,系统的稳定性及应对极端事件的抗压能力应给予高度关注。陈磊[8]的研究表明,各银行存款保险费率对资本充足率表现出了较高的敏感性,而各银行资本充足率受系统风险影响显著,从而存款保险费率应与系统风险水平具有较高的相关性。刘鸿伟[9]认为存款保险的目的是防范系统性风险,存款保险费率定价机制作为存款保险制度的重要部分,也应将目标聚焦于防范系统性风险。进一步,当经济形势恶化,整个银行业系统风险骤升[10],存款保险基金的充足性将受到极大挑战[11],如美国在2008年金融危机期间,联邦存款保险公司将银行5年间的破产成本预估上调了一倍。因此,在系统风险水平不同预期情况下测算各银行期望损失的变化,进而制定针对不同经济形势的存款保险风险费率,具有积极意义。
本文在风险中性测度下,将影响银行资产价值的风险因素分解为系统风险因素和银行特定风险因素,进而在不同系统风险因素点估计和区间估计条件下,推算各银行考虑系统风险因素的存款保险费率。
1 考虑系统风险因素的存款保险费率模型
1.1 基本假设
①资产价值:假设银行系统共有m家银行,在风险中性测度Q下,t时刻银行i的资产价值Vi(t)服从几何布朗运动,即有
dVi(t)=rVi(t)d+σi,vVi(t)dwi,v(t),i=1,2,…,m
(1)
其中,r为无风险利率,σi,v为银行i资产价值的即时波动率,wi,v(t)遵循维纳过程,dwi,v(t)表征了银行i资产的风险来源,相应风险大小由σi,v度量。 将银行i资产风险做如下分解
(2)
其中,dwY(t)表示影响银行i资产价值的系统性风险来源或宏观风险因素;dwi,ε(t)为银行i的特质风险来源,表示非系统性风险因素或银行特定风险因素;ρi(-1≤ρi≤1)表示银行i资产风险对系统性风险的敏感性;wY(t)和wi,ε(t)均服从维纳过程,且wY(t)与wi,ε(t)相互独立。
②投保存款价值:假设银行负债全部来源于存款,t时刻银行i的负债价值为Di(t),银行i为其部分存款购买存款保险,投保存款价值为Bi(t),且有Di(t)=βiBi(t),(βi≥1),即总负债价值是已投保存款价值的βi倍。Bi(t)为无风险资本,在风险中性测度Q下满足
dBi(t)=rBi(t)dt
(3)
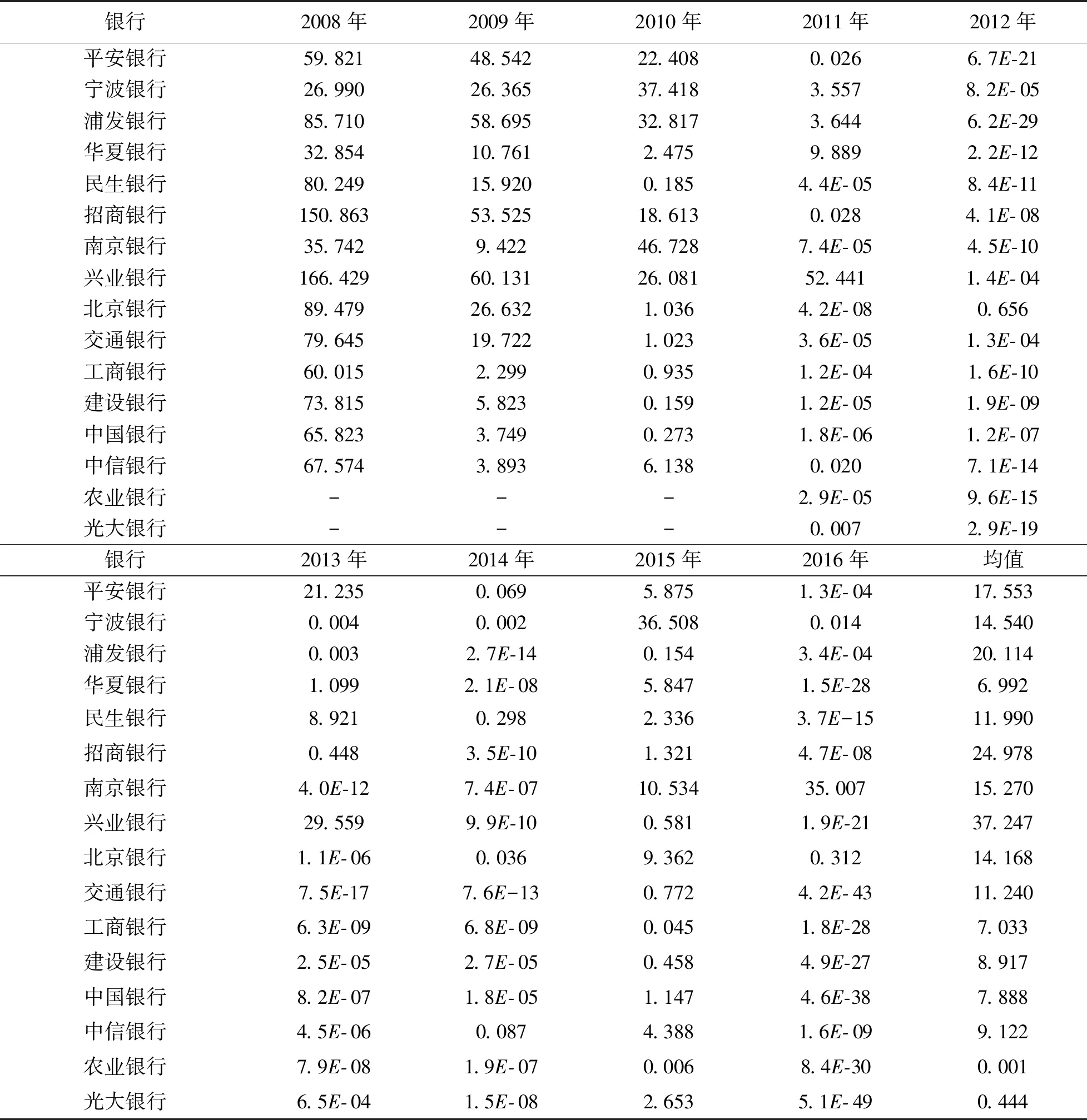
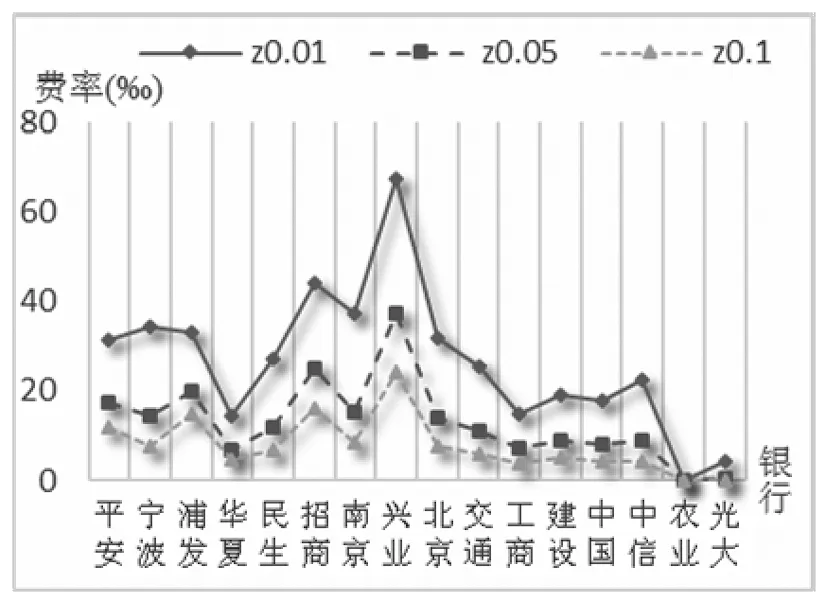
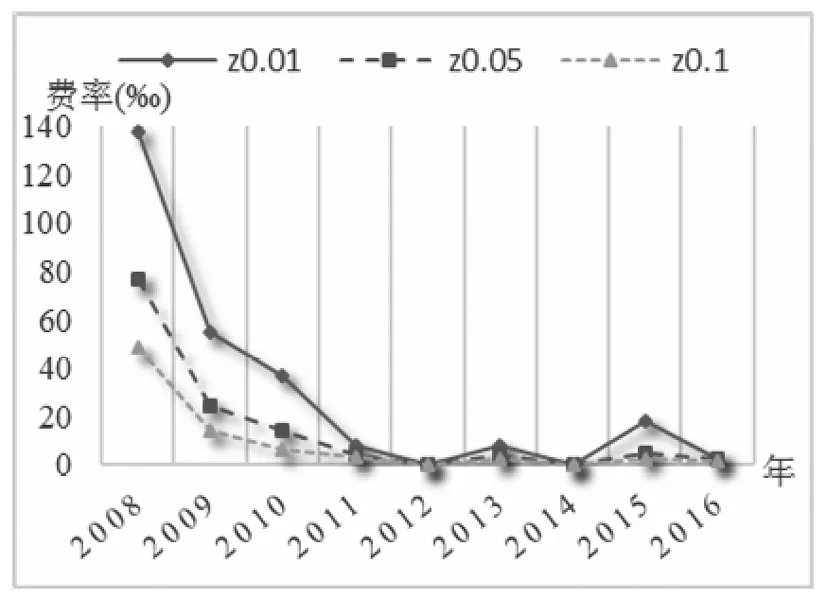
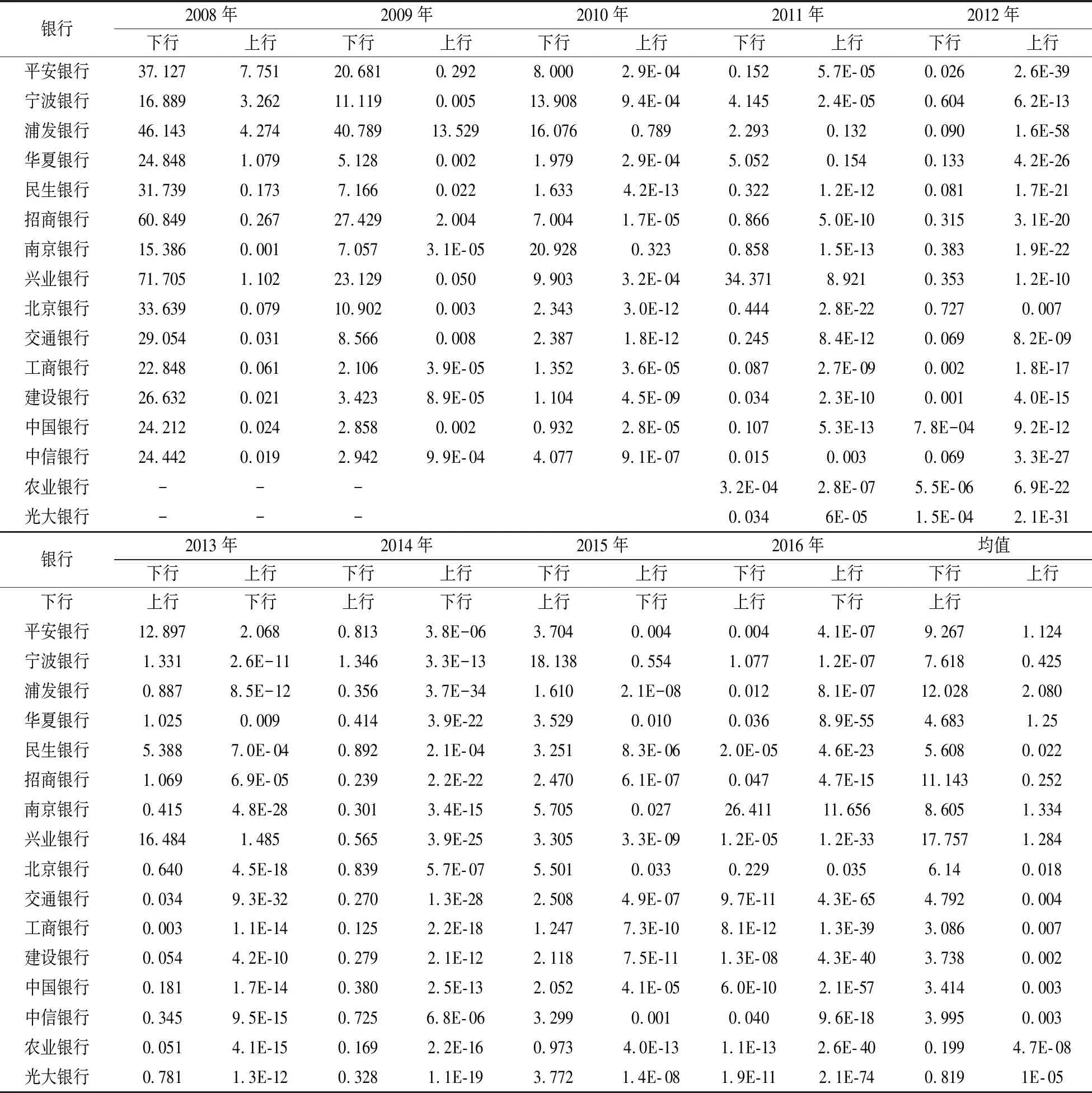
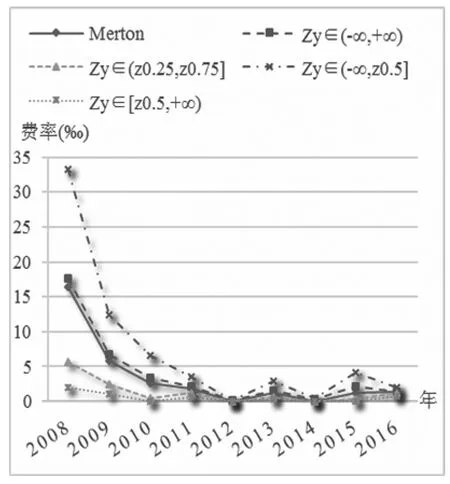
③存款保险:假设银行i在存款保险期末T时刻接受审查,若T时刻Vi(T)≥Di(T),则银行i经营状况良好,若Vi(T) (4) 式(4)给出了银行i存款保险的赔付责任,进一步整理得到 Li(T)=[Di(T)-Vi(T)]·{I[Vi(T) =[Di(T)-Vi(T)]·I[Vi(T) =max[Di(T)-Vi(T),0]-max[Di(T)-Vi(T)-Bi(T),0] 其中,I[.]为示性函数,当方括号内条件成立时,I[.]=1,否则I[.]=0。由风险中性定价原理知,基于上述赔付责任,期初0时刻银行i的存款保险总保费为 TPi=e-rT·EQ[Li(T)]=e-rT·EQ{max[Di(T)-Vi(T),0]}-e-rT·EQ{max[Di(T)-Vi(T)-Bi(T),0]} =e-rT·EQ{max[βiBi(T)-Vi(T),0]}-e-rT·EQ{max[(βi-1)Bi(T)-Vi(T),0]} (5) 其中,EQ[.]表示风险中性测度下的期望算子。 由伊藤定理,式(1)和式(3)可分别改写为如下形式 (6) dlnBi(t)=rdt (7) 式(6)与式(7)相减得到 (8) 在区间[0,T]内对式(8)两边积分得到 整理得到 (9) 将式(2)代入式(9),得到 (10) 进一步,当ZY=zy时,即系统风险因素在某一特定取值情况下,式(10)可表示为 (11) =EQ{max[βi-eXi(zy),0]} (12) =EQ{max[(βi-1)-eXi(zy),0]} (13) (14) 式(14)反映银行存款保险总保费与系统风险因素之间的相关关系,当银行系统风险敏感系数ρi=0时,式(14)退化为TPi=Bi(0)·[βiN(d1)-(βi-1)N(d3)]-Vi(0)[N(d2)-N(d4)],即为传统Merton存款保险期权定价公式。因此,实际上Merton存款保险定价方法是本文定价模型的特例。式(14)两边同除以投保存款总价值Bi(0),得到系统风险因素ZY=zy时,银行i单位存款的存款保险费率 (15) 应用式(15)确定各银行的实际存款保险费率,需要较准确的预测某年度的系统风险因素。然而,对系统风险因素的预测,很难精确到具体取值。更合理可行的定价方式是估计某年度系统风险因素可能的取值区间,进而在该特定区间内,计算各银行存款保险费率的条件期望值,以此作为特定系统风险区间估值条件下,银行存款保险的费率。给定系统风险因素的取值区间zy1≤ZY≤zy2,其中zy1和zy2为标准正态分布的分位数,且有N-1(zy1)=yl(l=1,2)。在此区间内银行存款保险费率的条件期望值表示为 EQ[PPi(ZY)|zy1≤ZY≤zy2] (16) (17) 最后,将系统风险因素离散化,当h取值足够大时有 (18) 将式(18)代入式(16),得到系统风险区间估计条件下,银行i存款保险费率 PPi(ZY∈[zy1,zy2]) =E[PPi(ZY)|zy1≤ZY≤zy2] (19) 由第1节推算方法知,估算银行存款保险费率需确定三方面参数:各银行资产波动率σi,V、各银行对系统风险因素的敏感系数ρi、以及各银行比例系数βi。其中,比例系数βi取各银行负债价值与总存款价值的比例,其余参数包括:银行资产波动率σi,V和系统风险敏感系数ρi。本节对以上两个参数进行估计,选取了十六家上市银行作为研究样本(见表1), 研究期间为2008~2016年度(由于农业、光大两家银行上市时间分别为2010年7月和2010年8月,因此这两家银行的研究期间为2011~2016年),计算数据取自国泰安CSMAR数据库。 由于各银行资产波动率的确定方法相同,故本节省略区分不同银行的字母i。假设银行在一年内具有同样的资产波动率,将一年期限分为N段,VI(I=1,2,…,N)代表第I个时段末银行的资产价值,H代表单个时段时长,一般以年为单位。由于每个时段末银行的资产价值VI不可观测,需根据可观测的上市银行股权价值进行估计[13]。设每时段末银行股权价值为SI,一年内银行股权价值的波动率为σS,SI可看作是一份标的资产为VI,执行价格为DN的欧式看涨期权的价值[14],DN为第N个时段末(即年末)银行的负债价值,SI与VI满足 SI=VIN(d1,I)-DNe-r[(N-I)H]N(d2,I) (20) (21) 式(21)给出了银行资产波动率σV与银行股权波动率σS之间的关系。在σS可估计的情况下,联合式(20)和式(21)即可估计出每个时段末银行的资产价值VI及资产波动率σV[11]。 以上估计方法仍需3方面数据:银行每个交易日的股权价值、每年年末的负债价值和每年的无风险利率。其中,银行每个交易日的股权价值等于银行总股本与其股票当日收盘价的乘积;负债价值取各银行每年年末总负债的账面价值;无风险利率取各银行一年期存款利率的均值。具体测算结果见表1。 表1 2008~2016年度各银行资产波动率 本节参考文献[12]、文献[15]的方法,根据银行间资产相关系数估计各银行对系统性风险因素的敏感系数。将式(2)代入式(1),且将式(1)中无风险利率替换成实际的银行资产收益率,即得到真实测度下各银行的资产价值过程 dVi(t)=μi,VVi(t)dt+ (22) 其中,μi,V为真实测度下银行i的资产收益率。 首先,构造统计量 (23) 由式(22)知,Ki,I服从标准正态分布,且有 (24) (25) (26) s.t. -1≤ρi≤1 (27) 表2 各银行系统风险敏感系数 本节分为三个层次:首先,在系统风险因素点估计条件下模拟各银行的条件费率结果;其次,在系统风险因素特定区间预期下测算银行面临的存款保险费率情况,研究经济形势不同情境下费率的变化趋势;最后,将传统的Merton期权费率与本文测算得到的费率结果进行比较分析,并在极端经济形势下进行压力测试。 取系统风险因素95%置信度下的分位数点z0.05=N-1(0.05),即有Pr(ZY>z0.05)=95%。将zy=z0.05代入式(15),其他参数取值见表1、表2,得到系统风险因素95%置信度下,16家上市银行2008~2016年度的存款保险费率,具体测算结果见表3。从结果看,各银行各年度内费率水平具有较大差别,同一年度内各银行存款保险费率的差别主要反映了各银行特定风险因素的不同,而同一银行不同年度内费率的差别则是银行特定风险因素和系统风险因素共同作用的结果。表3的费率结果可看作置信度为95%的费率水平,即有95%的概率实际发生损失不会超过测算的保费水平。 表3 系统风险95%分位数点取值下各银行存款保险费率(‰) 进一步,取系统风险因素90%(即zy=z0.1)和99%(即zy=z0.01)置信度下的分位数点计算各银行各年度的费率水平,并与95%置信度下得到的费率进行比较,具体结果见图1和图2。具体来看,图1表示三种不同置信度下,各银行九年间的平均费率水平,由于三种置信度均反映极端风险情况,因此图1实际上比较了各银行对不同极端系统风险的费率敏感程度。整体来看:①在三种置信度下,16家银行中兴业银行的平均费率均为最高,而农业银行的平均费率最低;②各银行费率对系统风险因素均表现出了负相关关系,即系统风险因素取值越低(对应风险水平越高),银行费率水平越高,体现了存款保险费率随系统风险增大而提高的趋势;③各银行费率对系统风险因素的敏感程度不同,其中华夏银行费率的敏感性相对较低,表现为不同置信度下费率水平差距相对较小,而宁波、交通和中信银行在系统风险因素较高时,费率有更大程度的增加。当宏观经济形势有下行趋势时,费率系统风险敏感度高的银行应当缴纳更高的费率。 图2显示了三种不同置信度下,各年度内16家银行的平均费率变化情况。结果显示:①在三种置信度下,2008年银行业的平均费率最高,2011年以后相对较低;②从平均费率来看,银行业在不同年度内对系统风险因素的敏感度不完全相同,其中2010年和2015年来看,银行业对高系统风险更加敏感,表现为较高系统风险下更高的平均费率水平。 综合来看,尽管费率水平对系统风险因素的敏感程度有差别,但不同银行、不同年度内存款保险的费率水平均对系统风险水平表现出了正相关关系。这一结果与现有研究跨期存款保险定价方法的相关文献结论一致。文献[8]和文献[16]的研究均显示,基于风险的存款保险费率在经济衰退期与经济平稳期具有相当显著的差别,即存款保险费率与表征经济形势的系统风险具有相当高的正相关关系。而由于银行系统内各银行的关联状况在不同年份内不尽相同,故银行存款保险费率对系统风险因素的敏感程度在不同年度内也会有所变化。 图1 不同置信度下各银行平均费率 图2 不同置信度下各年度平均费率 以系统风险因素均值(即zy=z0.5=0)为界,将系统风险因素可能的取值区间(-∞,0]分为两部分,当系统风险因素在区间取值时,表征经济形势下行的预期,相反,系统风险因素取值区间为[0,+∞)时,代表经济形势上行的预期。将相关参数代入式(19),得到系统风险区间估计条件下,16家上市银行2008~2016年度存款保险的费率,具体测算结果见表4。在不同经济形势预期下,各银行各年度内存款保险费率具有较大差别,经济下行预期下各银行的存款保险费率显著高于经济上行预期下的费率水平。对宏观经济形势的准确预期难度较大,“上行/下行”的基本划分虽比较模糊,但在此基础上计算的存款保险费率水平,能够在粗略估计经济形势前提下判断实际费率水平的充足性。当对下一年度经济形势有下行预期时,各银行实际缴纳的存款保险费率与表4列示的下行费率之间的差距,即为存款保险在经济形势下行期可能面临的费率缺口,这在存款保险制度建立初期的中国具有比较重要的意义。相反,当经济形势有显著上行预期时,银行实际面临的存款保险费率高于表4中上行费率的部分,相对流动性要求较低,可考虑差异性投资项目。 表4 系统风险不同区间估值下各银行存款保险费率(‰) 进一步,对系统风险因素进行不同的区间划分,可测算出银行不同经济形势下的平均费率水平。当系统风险因素取值区间为(-∞,+∞)时,得到无特定预期下各银行的存款保险费率(对应表5第2列),以此作为其他区间估计费率的比较基准,并在下一节与传统Merton期权定价方法下的费率进行比较。当系统风险因素在区间[z0.25,z0.75]取值时(对应表5第3列),得到经济形势平稳预期下的费率水平。当预期银行系统整体稳定,系统风险因素可能的取值集中在均值附近时,各银行的平均费率比无预期情况下的费率有明显下降,表现出系统风险尾部极端分布对费率影响的非对称性,即风险极高区间对费率的贡献远远大于风险极低区间,从而扣除两段尾部区间后,平稳区间内测算的费率水平有明显下降。 表5 系统风险因素不同区间预期下各年度银行业平均费率水平 更直观的结果见表5第4至第7列,将系统风险因素取值区间做更细致的划分,得到四个区间:(-∞,z0.25]、(z0.25,z0.5]、(z0.5,z0.75]和(z0.75,+∞],进而测算出经济形势强下行、弱下行、弱上行和强上行预期下银行的平均费率水平。与无预期基准费率比较,不仅经济形势上行两种情况下的费率水平显著较低,即使在经济弱下行预期下,测算得到的费率水平也远低于基准费率,而经济强下行预期下的费率水平远高于基准费率。 上述结果表明,极端经济形势对费率的影响具有非对称性特点,即风险极高区间对平均费率的贡献远远高于风险极低区间。文献[11]以美国1993年至2011年存款保险相关数据进行测算,发现当经济形势出现恶化时,以期望损失水平为基础确定的存款保险费率可能使基金存在很大缺口,即经济平稳期积累的基金难以支撑危机期资金的需求,这一结果与本文的结果具有一致性。这一结果至少具有以下启示:①为保证经济形势强下行情况下存款保险基金充足,需在经济平稳期和上行期做足够多的保费积累,因此在存款保险制度建立初期(无法满足积累期足够多),相关部门应作其他资金储备,以应对经济突发事件可能引致的存款保险基金充足性问题;②当经济形势平稳上行情况下,存款保险基金流动性要求相对较低,在保证基本流动性的基础上,应主动运用基金投资增值,以加快基金积累速度,以应对经济下行期基金的高额需求。 当式(15)中银行系统风险敏感系数ρi=0时,费率公式退化为不考虑系统风险因素的传统Merton存款保险期权定价公式。图3和图4给出了系统风险因素区间估计条件下银行存款保险费率与传统Merton费率的比较结果,其中,图3显示了9年间银行系统平均费率的比较情况,而图4以银行的角度出发,比较了16家银行9年平均费率的情况。从比较结果看:①不同系统风险因素区间估计下得到的费率结果与传统Merton期权定价法下的费率结果相比,无论从年均费率还是行均费率的角度看,都具有一致的趋势,表明该方法与Merton定价方法类似,能够在一定程度上反映各银行各年度的风险程度;②Merton定价法不考虑系统风险因素不同预期的影响,实际上相当于是在系统风险因素全概率的视角下,计算单个银行的风险费率,因此当系统风险因素取值区间为(-∞,+∞)时(对应3.2节无预期费率结果),本文方法估算出的费率结果与传统Merton定价法得到的费率结果具有高度一致性;③总体来看,考虑系统风险因素全概率区间的费率估算结果略高于Merton定价法下的费率,表明从银行受系统风险影响程度的角度计算费率,能够在一定程度上补偿银行间关联性引致的违约额外成本;④当系统风险因素有特定预期时,Merton定价法下确定的费率水平可能与各银行各年度实际面临的风险成本有较大差距。 传统Meton定价法费率的偏估问题,很多文献都有涉及。文献[17]以Meton费率为基础,在不确定环境下构建银行存款保险定价模型,研究结果显示随着不确定参数的增大,各银行保险费率区间长度都有增大的趋势,即不考虑不确定性的费率水平可能与真实风险情况相差很远。文献[8]基于宏观审慎监管框架构建存款保险定价模型,测算结果显示考虑各银行系统风险贡献情况下确定的费率水平,显著高于传统方法的费率水平。文献[5]和文献[6]的研究结果均显示,银行破产存在负外部效应,仅以单个银行破产损失为基础的Meton定价方法,忽略了破产的额外成本,因此费率可能存在低估。 图3 不同定价法下年度平均费率比较 图4 不同定价法下银行平均费率比较 最后,模拟经济形势极端情况下各银行年均费率的变化情况。取3.1节系统风险因素90%和95%置信度下的费率计算结果,度量极端风险情况下银行可能面临的风险成本。进一步,当经济形势有强下行预期时,取3.2节系统风险因素(-∞,Z0.25]区间估值情况下的费率结果,并与传统Merton期权定价法下的费率结果进行比较,具体结果见图5。结果表明:①当经济形势出现极端情况时,Merton费率与实际风险成本可能存在较大差距,经济形势越差,差距越明显;②在系统风险强下行预期下,运用系统风险区间估计下测算的费率与实际风险成本的契合度相对较好;③各银行对极端系统风险的敏感程度不同,进而传统定价法下费率低估程度也不同,其中华夏、农业和光大银行低估程度较低,而兴业和招商银行的低估程度最高。 图5 极端风险预期下Merton定价法、系统风险点估计定价法与系统风险区间估计定价法的比较 本文相关结论包括两部分: (1)银行存款保险费率与系统风险因素的关系,具体结论包括:①各银行风险费率对系统风险因素均表现出了负相关关系,但各银行费率对系统风险因素的敏感程度不同,其中华夏银行费率的敏感性相对较低,而宁波、交通和中信银行费率对系统风险因素更为敏感;②银行在不同年度内对系统风险因素的敏感度不完全相同,其中2010年和2015年总体来看,银行业对高系统风险因素更加敏感,表现为高系统风险因素下更高的平均费率水平;③经济形势尾部极端分布对费率的影响具有非对称性特点,即风险极高区间对平均费率的贡献远远高于风险极低区间的影响。 (2)系统风险因素不同预期下的费率与Merton费率的比较结果,具体结论包括:①系统风险因素全概率区间下测算的费率水平与Merton费率相比,处于略高且非常接近的趋势,较高的费率能够适度补偿银行间关联性导致的违约额外成本;②当经济形势有较明朗预期时,Merton定价法下确定的费率水平可能与各银行各年度实际面临的风险成本有较大差距,当经济形势出现极端情况时,系统风险区间估计下测算的费率与实际风险成本的契合度相对较好;③各银行对极端系统风险的敏感程度不同,进而Merton定价法下费率低估程度也不同,其中华夏、农业和光大银行低估程度较低,而兴业和招商银行的低估程度最高。 上述结论至少在两个方面具有启示作用:①传统的Merton费率较接近于不对系统风险因素进行任何预期下确定的费率水平,因此在存款保险制度推行的初期,一旦出现极端经济形势,存款保险基金的充足性将受到挑战;②由于不同年度不同银行对系统风险因素的敏感程度不同,不考虑系统风险因素的定价方法难以准确反映银行违约风险随经济形势波动的变化情况,系统风险因素不同预期下确定的费率有助于提升费率的针对性和公平性。 另外,本文提出的存款保险费率测算方法存在一定的局限性:首先,由于我国上市银行数量有限,且相关数据在2008年以后才相对完整,故本文参数估计能获取的数据相对偏少,且非上市银行的推广方法仍需进一步研究;其次,各年度银行系统风险因素如何确定,仍缺少实证研究相作证。随着我国存款保险制度的运行及相关数据的进一步完善,本文提出的费率测算方法可作进一步调整和完善。1.2 系统风险点估计条件下存款保险费率的推导

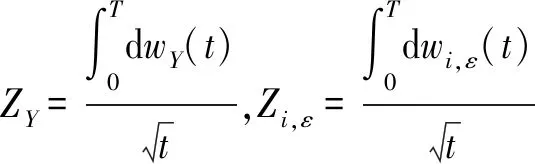

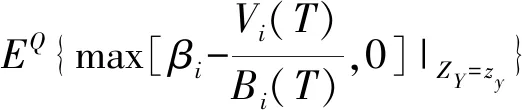
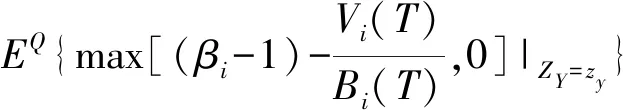


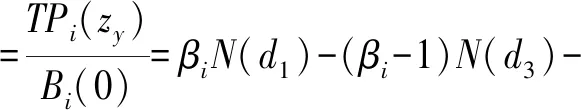
1.3 系统风险区间估计条件下存款保险费率的推导
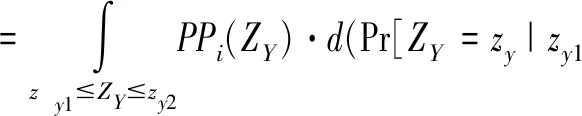
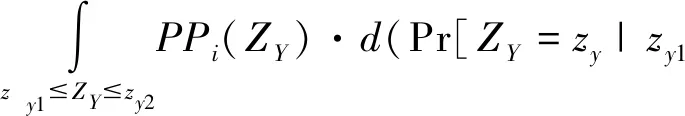
2 参数的确定
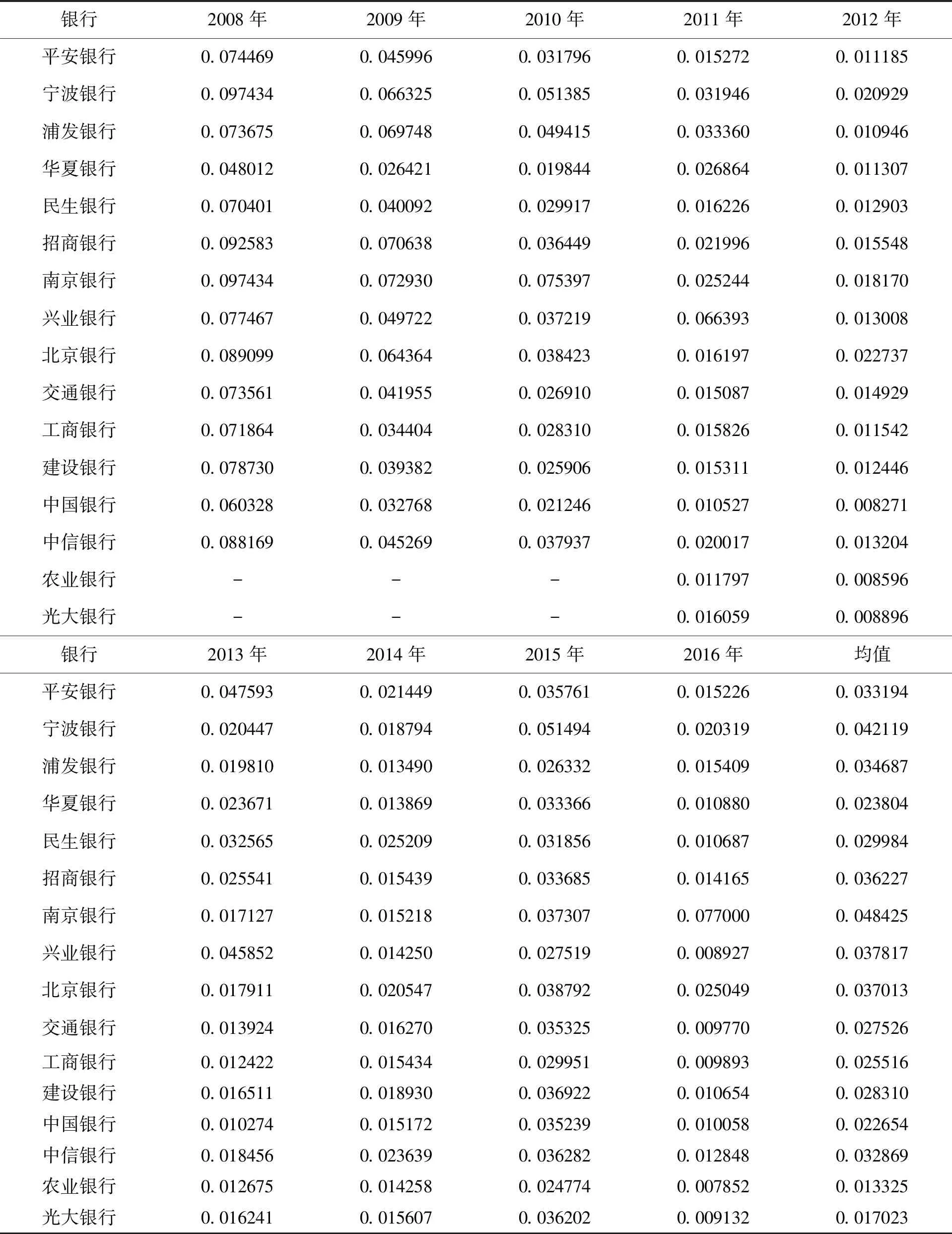
2.1 银行资产波动率的估计方法
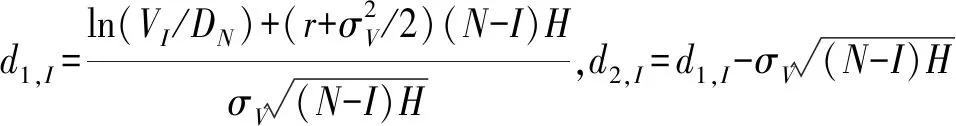
2.2 系统风险敏感系数的确定
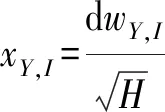

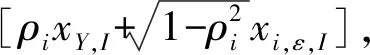


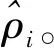

3 模拟分析结果
3.1 系统风险点估计条件下的费率测算结果
3.2 系统风险区间估计条件下的费率测算结果

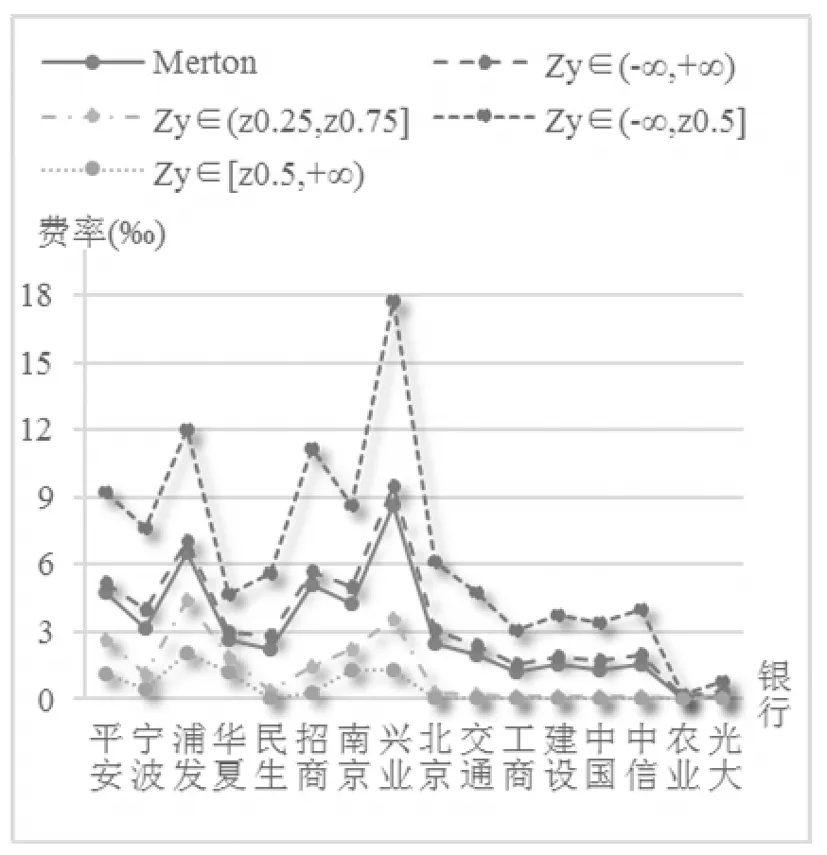
3.3 系统风险不同预期下的费率与传统Merton费率的比较

4 结论
