基于犹豫倾向聚类的物流中心选址方法
2019-04-09段冠华崔春生
段冠华, 林 健, 崔春生
(1.福建农林大学 计算机与信息学院,福建 福州 350002; 2.北京物资学院 北京市智能物流系统协同创新中心,北京 101149)
0 引言
Zadeh在模糊集[1]一文中,引入模糊集的隶属函数和非隶属函数概念。考虑到现实生活当中不总是非此即彼,还存在介于两者之间的犹豫、模糊情形。因此,保加利亚学者Atannssov[2]对模糊集进行了推广,同时考虑隶属度、非隶属度和犹豫度这三个方面。由于现实生活问题变得越来越复杂,直觉模糊集非常适合于在复杂的情况下表示模糊信息和不确定环境。由此引发国内外学者广泛研究,并成功在诸多领域[3~8]中得到了应用。然而,关于直觉模糊聚类研究方法的还较少。
作为直觉模糊集核心理论之一的相似性度量,许多学者从不同的方面进行了深入的研究。针对Chen[9]的相似度量方法在某些情况下不适用,Hong[10]等人提出改进方法;李凡[11]等人指出Hong和Chen在测量相似度时所存在的缺陷并给出一种新的相似度量方法;Li[12],Mitchell[13]和Li Dengfeng[14]等人进一步完善了直觉模糊集间相似度量的公理化定义。文献[9~14]在某些情况下存在直觉指数所表征的中立证据中支持与反对的程度呈均衡或之差呈均衡状态无法表述的问题。此外,Gao[15]和Hwangad[16]等人分别从Vague集和Sugeno积分讨论了相似度量,Iancu[17]则基于T范数提出了一些相似度量公式。然而在文献[9~16]中都忽视犹豫度的倾向性问题,从而易导致信息的扭曲与失真,丢失部分信息,公式缺乏灵活性。
本文首先提出了考虑带倾向性相似度的直觉模糊相似度量公式,构建具有倾向性的相似矩阵。利用平方法求等价相似矩阵,通过对等价相似矩阵的λ-截取进行聚类的新颖方法。并应用于物流中心选址,使得从备选地址中选取的地址为最佳。
1 预备知识
为了引入后续讨论,下面介绍一些关于直觉模糊集的基本概念。
1965年, Zadeh首次提出模糊集理论来处理不确定信息。
定义1[1]设X是一个非空集合,则称
F={
(1)
为模糊集,其中μF:X→[0,1]是元素x关于模糊集F的隶属度函数。
考虑到现在生活中的犹豫与不确定性,Atannssov对模糊集理论进行了扩展。
定义2[2]设X是一个非空集合,则
A={
(2)
为直觉模糊集,其中μA:X→[0,1],vA:X→[0,1]分别为X中元素x关于A的隶属度和非隶属度。且满足
0≤μA(x)+vA(x)≤1,x∈X
(3)
X中元素x关于A的犹豫度
πA(x)=1-μA(x)-vA(x),x∈X
(4)
X上所有直觉模糊集的集合记为:IFS(X)。
定义3[18]设α=(μα,vα)是一个直觉模糊数,其得分函数为:
s(α)=μα-vα
(5)
其中0≤μα-vα≤1,μα,vα≥0。
2 具有倾向性的直觉模糊相似度量
许多学者对相似度概念有不同的理解,因此在文献[19]中结合模糊相似度量的定义方法,给出直觉模糊相似度量的公理化定义。考虑到倾向性对犹豫度的影响,提出具有倾向性的直觉模糊相似度量公式,并扩展到连续的空间。
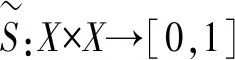
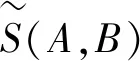
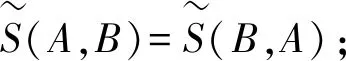
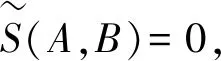
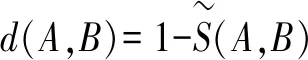
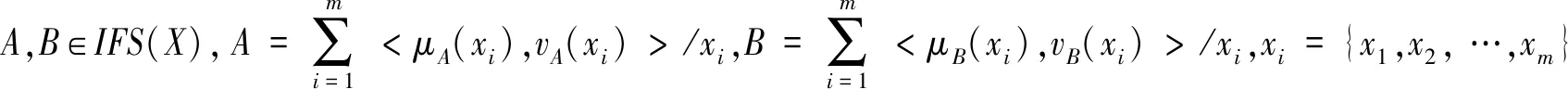
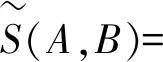
|vA(xi)-vB(xi)|)-
α|sA(xi)-sB(xi)|-
(6)

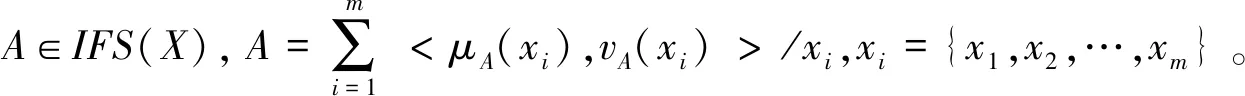
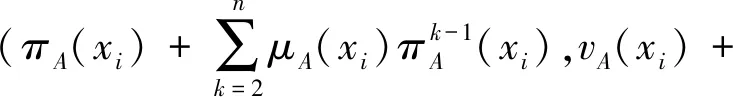
(6)
因此,我们提出了具有迭代倾向性的直觉模糊相似度量公式:
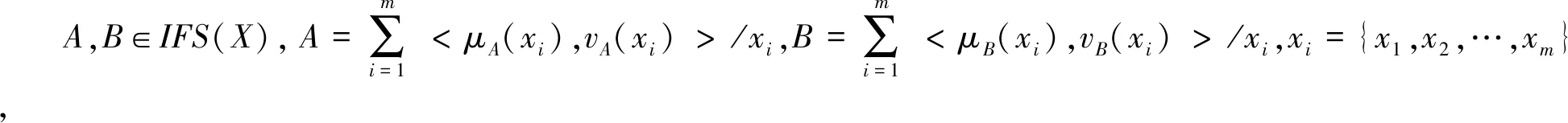
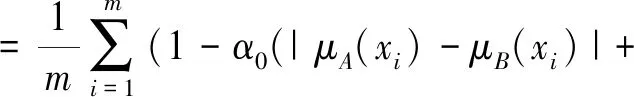
(8)
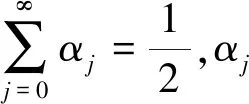
定理2∀A,B∈IFS(X),S(A,B)是直觉模糊集A,B之间的相似度。
证明(1)∀xi∈X,有μA(xi),vB(xi)∈[0,1],|μA(xi)-vB(xi)|∈[0.1],同理|vA(xi)-vB(xi)|∈[0,1],易知0≤|μA(xi)-μB(xi)|+|vB(xi)-vB(xi)|≤2,即|μA(xi)-μB(xi)|+|vA(xi)-vB(xi)|∈[0,2]。知s(A)∈[-1,1],s(B)∈[-1,1],当πA(xi)≠1时,

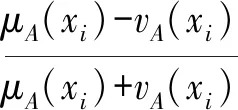
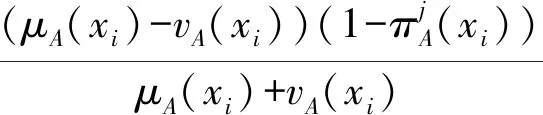

(2)由公式可知,显然S(A,B)=S(B,A)。
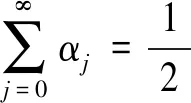
(4)设d(A,B)=1-S(A,B),即
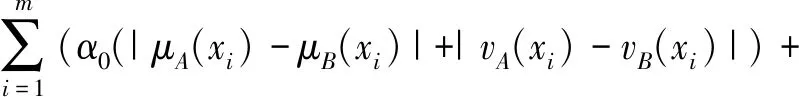
∀C∈IFS(X),有
d(A,C)+d(B,C)
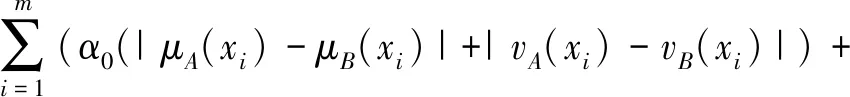
=d(A,B)
考虑到现实生活中迭代次数的有限,迭代次数越多,犹豫度对整体的影响越来越弱,我们给出了有限迭代的公式如下:
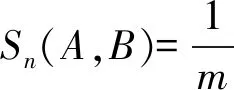
(9)
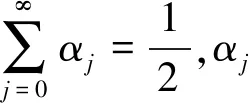
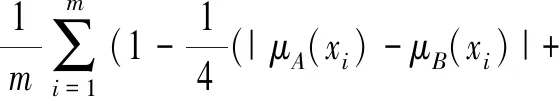
(10)
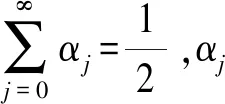
现实生活中不总是离散的,我们把离散空间的具有倾向性的直觉模糊相似度量延伸到连续空间具有倾向性的直觉模糊相似度量。
定义6∀A,B∈IFS([a,b]),A={
(11)
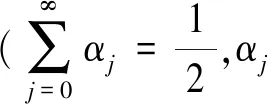

(12)
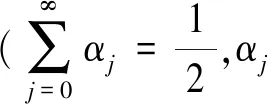
同样的,根据定理2的证明过程对定理3进行类似证明,这里不再赘述。
3 考虑带倾向性相似度的直觉模糊聚类方法
模糊聚类是依据事物间的属性、亲疏程度、相似性和距离,通过建立模糊相似关系对客观事物进行分类的方法。然而模糊聚类不能够更加细腻地描述和刻画客观世界的模糊性本质[20],直觉模糊聚类能够对信息进行有效的集成和处理。
3.1 等价相似矩阵与λ-截矩阵
定理4根据具有倾向性的直觉模糊相似度量式建立矩阵C=(cij)n×n,其中
cij=Sn(Ai,Aj),(i,j=1,2,…,n)
(13)
则矩阵C为相似矩阵。
证明1)自反性。∀i=1,2,…,n,由公式可知Sn(Ai,Ai)=1,即cii=1。2)对称性。由定义4可知Sn(Ai,Aj)=Sn(Aj,Ai),即cij=cji。
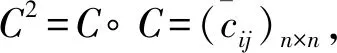
(14)
经过有限次合成:C→C2→C4→…→C2k→…,必定存在一个正整数k,使得C2k=C2k+1,且C2k为等价相似矩阵。
定义7[21]设C=(cij)n×n为等价相似矩阵,则称Cλ=(λcij)n×n为的λ-截矩阵,其中
(15)
且λ为置信水平,λ∈[0,1]。
3.2 方法步骤
在n个对象中,考虑m个特征信息,其特征信息用直觉模糊集表示,如表1。

表1 对象特征信息
对应特征信息直觉模糊矩阵为:
通过公式计算得到相似矩阵,经过有限次合成得到等价相似矩阵,在不同的置信水平下进行聚类,得到不同的类别 。下面给出具有相似度的直觉模糊集聚类方法具体步骤:
输入:对象特征信息直觉模糊矩阵A及λ值;
输出:对应λ值的聚类。
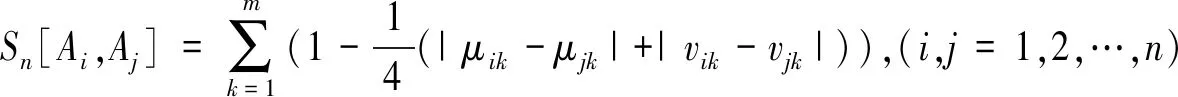
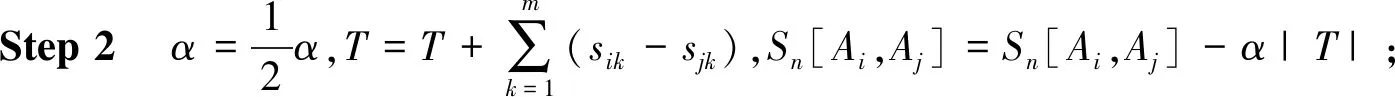
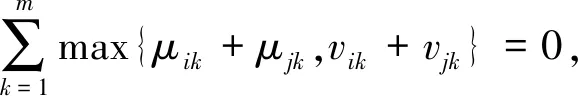
Step4更新数值,μik=μik+μikπik,vik=vik+vikπik,μjk=μjk+μjkπjk,vjk=vjk+vjkπjk,sik=μik-vik,sjk=μjk-vjk;
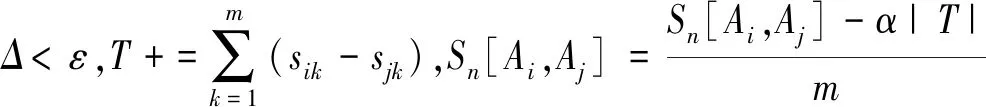
Step7如果Sn[i,j]不等于C[i,j],(i,j=1,2,…,n),则Sn[i,j]=C[i,j],(i,j=1,2,…,n),跳到Step6;
Step8利用公式(15)构造C的λ-截矩阵Cλ=(λcij)n×n;
Step9若Cλ中第i行(列)中所有元素与第j行(列)中对应的元素均相同,则直觉模糊集Ai和Aj是同一类。
4 物流中心选址应用
随着互联网技术的发展,电商服务越来越广泛,物流运输随之增多。而物流中心选址更是物流网络中心的重中之重。选址是否合理直接影响到物流系统的顺畅性、经济效益和运营效率。合理的选择物流中心能够对优化运输线路、降低物流成本、促进区域发展等方面起到重要的作用。
设某物流企业拟在福建建立一个对台大型物流中心,根据相关专家分析并结合企业决策者的建议,选取指标有自然条件、交通便利性、经济性、环境协调性和外部关联性。备选地址有A(福州)、B(泉州)、C(厦门)、D(漳州)、E(莆田)、F(宁德)六个城市。结合各地址的指标契合度和专家评价,得出各备选地址指标数值如表2:

表2 各备选地址指标
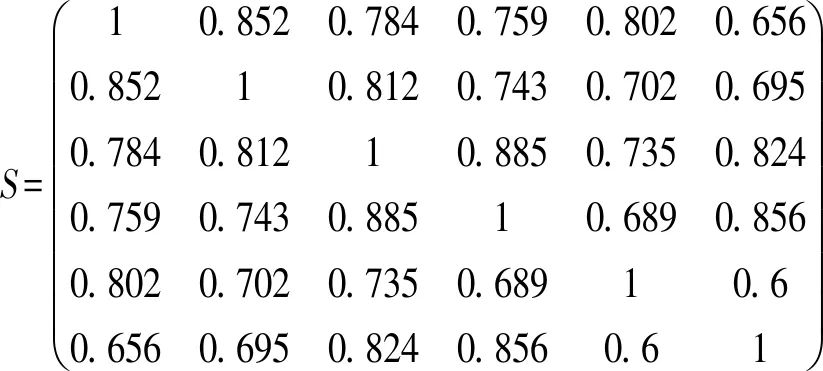
(i)通过公式计算得到相似矩阵S:
(ii)利用公式经过合成得到等价相似矩阵:
(iii)根据λ值不同对等价相似矩阵进行截取
a)0≤λ≤0.802时,备选地址为一类:{A,B,C,D,E,F};
b)0.802<λ<0.812时,备选地址分为二类:{A,B,C,D,F},{E};
c)0.812<λ≤0.852时,备选地址分为三类:{A,B},{C,D,F},{E};
d)0.852<λ≤0.856时,备选地址分为四类:{A},{B},{C,D,F},{E};
e)0.856<λ≤0.885时,备选地址分为五类:{A},{B},{C,D},{F},{E};
f)0.885<λ≤1时,备选地址分为六类:{A},{B},{C},{D},{E},{F}。
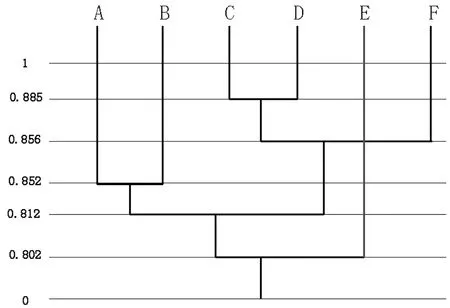
图1 直觉模糊聚类图
由聚类结果可知,当λ取值不同区间范围时,备选地址分类结果也不同。其中在b),c) ,d),e),f)中(即λ>0.802),E(泉州)选址为一类,则说明备选地址E(泉州)是该地区建设物流中心的最佳选址。通过对表2并结合实际情况分析,发现备选地址E(泉州)自然条件、交通便利性和环境协调性较好,经济性和外部关联性最好,是建设物流中心的最佳选址。备选物流中心E(泉州)符合战略性原则、经济性原则、实用性原则、协调性原则和可持续发展原则。
5 结论
本文针对某些情况下直觉指数所表征的中立证据中支持与反对的程度呈均衡或之差呈均衡状态无法表述的问题,并结合犹豫度的倾向性问题,提出了新颖的具有倾向性的直觉模糊相似度量公式,使其表示的信息更加全面,对事物分析更精确;根据实际问题可取不同的值,使公式灵活性和适应性增强。利用平方法求相似矩阵传递闭包收敛速度快的特点,使得基于倾向直觉模糊聚类在大数据环境下也能够快速得到分类结果。根据不同的值,可对物流中心选址范围进行粗细不同的划分,从而选出最佳的物流中心地址。
