有效因子综合偏好强度与CVaR整合优化模型

黄东宾， 周丹丹， 汪 涌

(重庆邮电大学 经济管理学院，重庆 400065)

0 引言

随着中国经济的开放与发展，中国股市体量的世界领先地位、投融资理性日趋成熟，是可以期待的未来。任何模型用于管理的资产规模有限，有效性也会衰减[1]，投资者对股市投资分析模型的需求也因此持续多样。市场中运用模型分析的投资者多了，投资者的金融知识、投资理性和市场效率也会相应增加[2,3]。因而，发展投资模型在中国股市的可用性，与期待投资者的投资理性，逻辑上应是一致的。

理性投资者的“事前”投资功效，是投资决策时对可获取数据及偏好等信息的综合描述，而投资功效的“事后”检验指标一般是收益率。“事前”投资理性应该充分包含与收益率相关的变量或因子[4]，通常涉及价值、动量、成长、规模、和分析师预测等多类别因子。与价值因子相关，持有低市盈率以期望高收益率，几乎是投资共识；市净率、市现率、市销率和账面市值比等其它价值因子也有效地用于股票价值投资策略构建[5]；在价值因子之外，股票收益率动量效应和反转效应，也普遍而不同程度地存在于全球股票市场[6]，但关于动量效应的有效期、驱动原因，文献解释不尽相同[7～12]。从多因子分析的角度，Asness等[13]则揭示了价值与动量的混合策略投资组合，相较于单一价值策略或动量策略，具有更显著的盈利水平。

对于规模因子，市值较小公司的股票平均收益率一般高于市值较大的公司[14]；Cakaci等[15～17]将规模因子与价值和动量因子综合分析，发现规模因子在发达资本市场和中国股市有效，但在其它新兴市场无效。另外，盈利能力、流动性、营业效率等成长类因子的有效性也得到检验[18～20]。

随着金融大数据分析技术的发展，分析师预测变量，尽管一定程度上会受分析师本人利益动机与偏见的影响[21]，也经常作为股票特征因子应用于资产配置决策分析中。研究显示综合采用上市公司基本面、动量变量、以及分析师预测变量是一个有效的长期投资策略[22]。

由于单一或单类因子仅限于股票局部特征描述，多因子投资分析应成为增强投资建议稳健性的有效途径之一。如何在现实市场数据中选择并融合有效多因子数据，整合形成多因子投资组合优化模型，是本文的研究问题。

关于多因子数据融合方法，量化投资中常采用因子打分法，即股票在不同因子上分别按偏好方向或优劣排序、按序计分，线性加权计算任一股票的多因子复合评分[18]。因子打分法最重要的缺陷是，以按序评分度量股票优劣，导致各因子实际数值的信息丢失；指标较多时，也会因权重不确定而缺乏稳健性。

其它多属性决策分析方法，如ELECTRE-TRI多指标综合分类方法、PROMETHEE多指标综合偏好排序方法，在股票选择和投资组合分析中虽有成功应用[23,24]，但前者在每个指标上都涉及多个类别阈值，及相关隶属程度等参数设定，后者则在每个指标上都涉及偏好隶属函数等多个参数设置，因而两者在指标较多情形下，因涉及过多参数而不具可操作性；数据包络分析(DEA)的交叉效率评价方法也被应用于融合多因子信息进行投资组合优选[25～27]，但是DEA方法按照类似投入产出逻辑，需要明确界定输入和输出变量，从而具有变量选择性，不利于变量因子的灵活处理。

本文规避上述参数过多和变量选择性的缺陷，从股票多维特征因子中选择部分因子，综合形成有效因子综合偏好强度(Integrated Preference Strength, 缩写为IPS)，并构建最大化IPS的附加理性，构建并验证IPS-均值-CVaR投资组合优化模型。

1 方法与模型构建

1.1 有效因子及其检验步骤

为说明有效因子检验方法，参照Fama和French[28]的因子分析方法，定义如下概念：

定义1单因子组合 令股票个数n的样本空间，按投资组合调整周期，依照所有股票任一因子t-1周期的因子值，从小到大排序，按序等位均分m组，记为G1,…,Gm(n>>m)，每组含n/m只左右股票 (若组届附近两个以上股票排序相同，则等概率随机划分至相邻组别)，各组按等权重构建投资组合，构成m个投资组合P1,…,Pm，称单因子等权重组合，简称单因子组合。

定义2单因子优势组合 根据t-1时期任一因子值构建的m组单因子组合中，比较两端组合P1，Pm在t时期的平均收益率，即μP1-μPm，若为正，P1为单因子优势组合；反之，Pm为单因子优势组合；若为零，则当期无优势组合。

在单因子组合两端P1，Pm中选择优势组合是基于有效因子偏好单调假设，即任何因子的优化或偏好方向是单调递增或递减，或可以转化为单调递增或递减。例如，若存在因子x的偏好准则是越接近x0越好，则可将因子转化为x′=|x-x0|单调递减的优化或偏好方向。

定义3有效因子 同时符合以下标准的股票特征因子为有效因子：(1) 单因子优势组合超额收益率在95%置信水平显著为正；(2) 单因子优势组合取得超额收益率的频率不低于60%；(3) 单因子分组序数与相应分组的年化收益率为强相关，正相关则相关系数大于0.6，负相关则小于-0.6。

有效因子检验步骤如下：

(1)分组计算单因子组合月收益率；

(2)确定单因子优势组合；

(3)月超额收益率显著性检验：各组单因子优势组合与市场基准做配对样本t检验， 置信水平设定为95%；

(4)超额收益率的频率检验：统计因子优势组合取得超额收益率的频率；

(5)相关性检验：计算每月五组因子组合序数与因子回报排名的相关系数并判断强弱。

以(3)、(4)、(5)步骤结果，按前述定义标准，判断有效因子。

1.2 有效因子综合偏好强度

有效因子是从候选因子中筛选出来，具有更优信息价值和预测能力的股票收益率影响因子。有效因子信息的融合，我们运用熵权-TOPSIS方法计算有效因子综合偏好强度，用于股票优选和投资组合优化模型的构建。TOPSIS方法通过在备选集中构建正理想点与负理想点作为双基点，对集合中n个决策单元在m维度上按如下原理综合计算排序。

备选集合中所有有效因子最优值构成(虚拟)正理想点，所有最劣值构成负理想点。计算备选单元与正、负理想点的加权欧式几何距离，定义多因子选择偏好强度(定义4)，离负理想点越远、正理想点越近为最大偏好强度，反之为最小偏好强度。各因子权重应用熵权法根据数据本身所含信息进行客观计算。熵权法是一种客观赋权法，能够充分的利用系统内的信息，减少人为主观性。将两者结合构建熵权TOPSIS模型进行多因子综合评价，具体步骤参照Hwang等[29]和黄东宾等[30]。

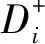
1.3 IPS-均值-CVaR投资组合优化模型

假设最大化期望收益(μ)、最小化条件风险值(CVaR)、和最大化综合IPS值(V)为投资理性，则用于求解投资组合资产配置向量(x)的优化模型构建如下：

(1)

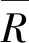
(2)

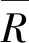
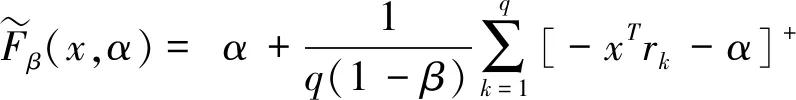
通过理论推导、软件仿真及实验分析，研究了泄漏对于液压系统流量、速度的影响；推导出了泄漏对于速度的影响表达式，为今后系统的研究提供了更好的参考；基于AMESim建立了调速阀进油节流调速回路仿真模型，仿真研究了外加负载对液压缸泄漏以及泄漏量对活塞速度的影响，得出了负载-流量、负载-速度、流量-速度曲线。

(3)

2 沪深300有效因子的选择

2.1 样本及候选因子

以沪深300成分股为样本，依前述有效因子检验方法，对于所有候选因子，将300个成份股分成5组单因子组合，由于沪深300成分股会定期按规则调整，会有剔除或新的编入，因此在收集数据时应依据历史实际情况对样本总体作一致对应。数据收集时段为2006年初至2015年末(数据来源WINDTM资讯)；在此期间沪深A股经历了几轮波动周期，既有牛、熊市交替，也有相对平稳期，有利于检验在多种市场动态环境下的因子与模型效果。令投资组合调整周期为月，月终交易日收盘后分析构建下一期组合。基于前述文献综述，选取包含规模、价值、成长、动量以及分析师预测等五类因子的15个变量作为候选因子，如表1第1、2列所示，各指标变量的说明可参见文献[33]。

2.2 因子有效性检验结果

按上述有效因子检验步骤对所列15个候选因子依次检验，结果如表1所示。

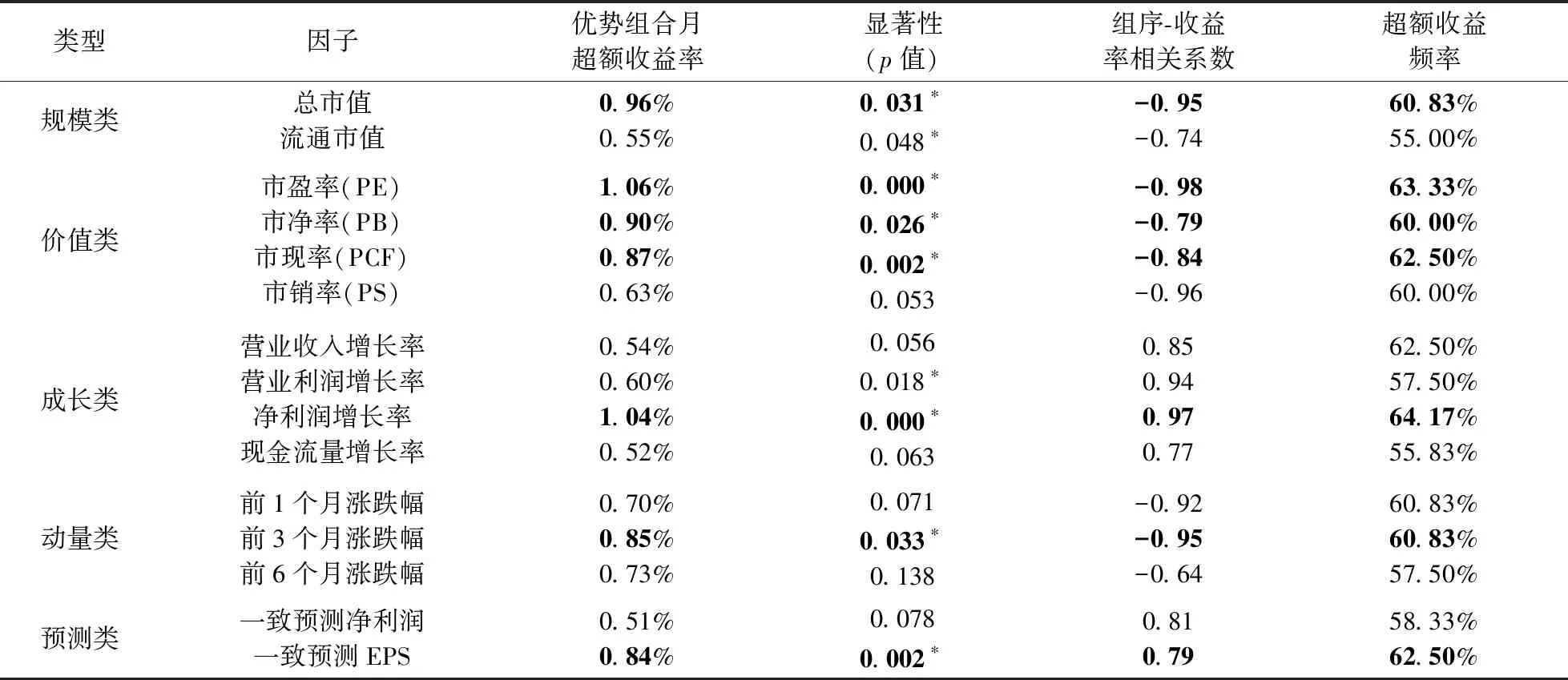
表1 候选因子及其有效性t检验统计结果

注：标*的数据表示95%置信水平下显著；粗体所示为通过有效因子检验。

检验结果显示，总市值和流通市值低的资产组合表现更优的盈利能力，其优势组合月超额收益显著为正，组序与收益率负相关；超额收益发生频率上，总市值因子通过检验，而流通市值因子未通过检验。 四个价值类因子均与收益率负相关，其中市盈率、市净率和市现率优势因子的月超额收益率显著为正，但市销率因子优势组合的月超额收益率未通过显著性检验。成长类因子与收益率呈正相关，营业利润增长率、和净利润增长率因子的优势组合，其月超额收益率通过了显著性检验，只有净利润增长率符合所有三项有效因子检验条件。三个动量类因子与收益率负相关，表明市场的确具有一定的动量反转效应。其中，三个月动量因子符合有效因子检验条件。预测类因子中，预测净利润因子未通过显著性和基准超越频率的检验，一致预测EPS因子通过有效因子检验。

综上所述，根据表1粗显所示结果，选择出7个有效因子，用于计算有效因子综合偏好强度IPS。

3 模型应用结果与讨论

在有效因子选择基础上，以下验证：1)IPS投资组合，是否比任何有效因子单因子组合表现更好？2)IPS方法是否优于常用的因子打分法？3)有效因子综合偏好强度最大化，作为附加理性融入风险收益优化模型，是否具有更好的投资组合表现？

3.1 IPS投资组合比单因子组合表现优越

IPS投资组合构建：依定义4，应用熵权-TOPSIS方法，每个调整期开始(月初)计算备选样本7个有效因子的综合偏好强度(IPS)，自大到小选取排序前30的股票，等权重构成当期IPS投资组合；

有效因子单因子投资组合构建：同样，将7个有效因子，分别按偏好或优化方向从大到小排序。根据表1结果显示，总市值、市盈率、市净率、市现率、三个月动量因子在资产选择背景下，其优化方向为最小化，宜从低到高排列；而净利润增长率、一致预测EPS因子，其优化方向为最大化，宜从高到低排列；分别选取排名前30的股票，等权重组成对应的单因子投资组合。

对比以上类别投资组合的绩效指标，结果如表2所示。

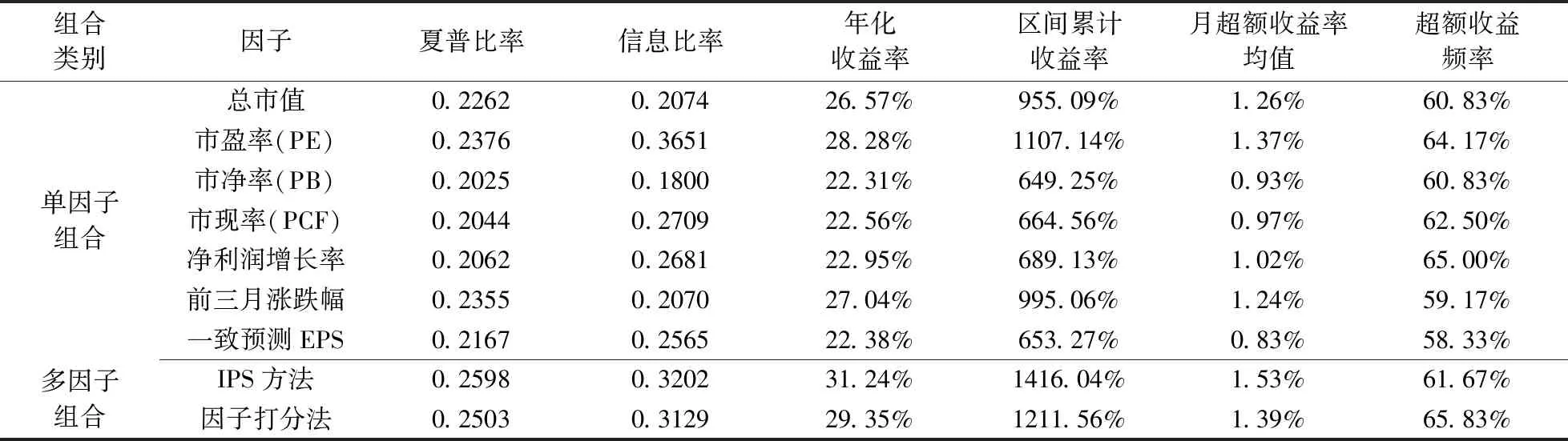
表2 不同因子组合的绩效对比

注：数据跨度2006年1月至2015年12月，样本空间为沪深300成份股，投资组合调整周期为月

从盈利性角度看，IPS投资组合在累计收益率、年化收益率、月收益率均值以及月超额收益均值均超越所有7个有效因子单因子组合，累计收益率优势最为显著(图1)；从风险收益比角度看，IPS投资组合与其它单因子投资组合相比，夏普比率和信息比率均显示优势；表明IPS投资组合显著优越于单因子投资组合。

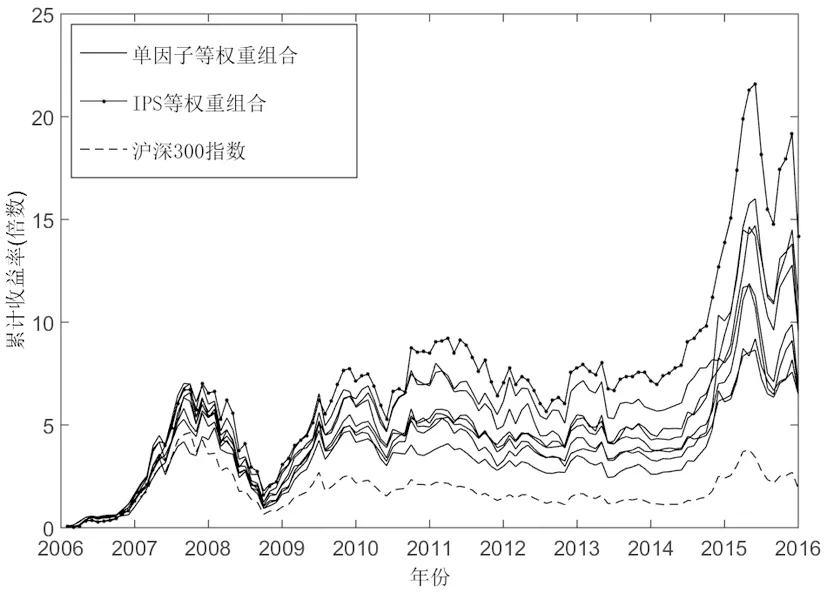
图1 IPS投资组合与单因子投资组合累计收益比较

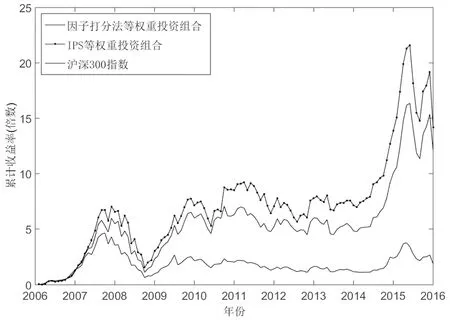
图2 IPS方法与因子打分法产生的等权重投资组合累计收益比较

3.2 IPS方法相对于因子打分法的优越性

多因子投资组合常用因子打分法计算复合得分(composite score)[18]，即是将因子数值按偏好方向从大到小排列计分，排名1，得分记为1，排名n，得分记为n，备选股票所有因子得分的均值为此股票的复合得分；得分越低，偏好排名越靠前。选择排名前30的股票组成当月的打分法多因子投资组合，与基于熵权-TOPSIS方法计算的有效因子综合偏好强度多IPS投资组合进行对比。两类投资组合的绩效对比(参见表2)显示，IPS投资组合在盈利性和风险收益率上均优于因子打分法投资组合，在跑赢市场基准频率上略输后者，两种方法产生的投资组合累计收益走势如图2所示，IPS方法对比常用的因子打分法总体表现更优越。

3.3 IPS-均值-CVaR模型的优越性

以上IPS等权重投资组合，缺乏风险度量及风险-收益优化，不能支持针对不同风险偏好的投资组合选择，反映的投资理性也是局限的。以下检验IPS-均值-CVaR投资组合优化模型的优越性。

针对前述模型(2)、(3)，设定多组权重(λ1,λ2)，分别表示目标函数中CVaR的权重，和投资组合IPS综合值V(x)的权重，如表3第1列；设定任意投资组合股票数量下限SL为15，上限SU为30，投资权重下限WL为0.01，权重上限WU为0.1。投资组合调整周期为每月一次，每期计算CVaR和投资组合有效前沿采用股票前两年日收益率，在有效前沿取夏普比率最大的投资组合，作为调整时的投资决策，并用样本外数据即调整后一个月(持有期)的数据，逐月追踪每一期投资组合的持有期收益率(注：样本内数据为每期投资组合调整时的“历史”数据，而假设此后一个月，即调整后的投资组合的持有期数据未知；所以用于检验投资组合调整效果的“后一个月”数据为样本外数据，如此逐期类推)；对比从2006年1月至2015年12月，多种权重组合情景的IPS-mean-CVaR模型优化投资组合、IPS等权重投资组合，以及未采用IPS优选的mean-CVaR基准模型的表现(取夏普比率最大的投资组合)，结果如表3所示。

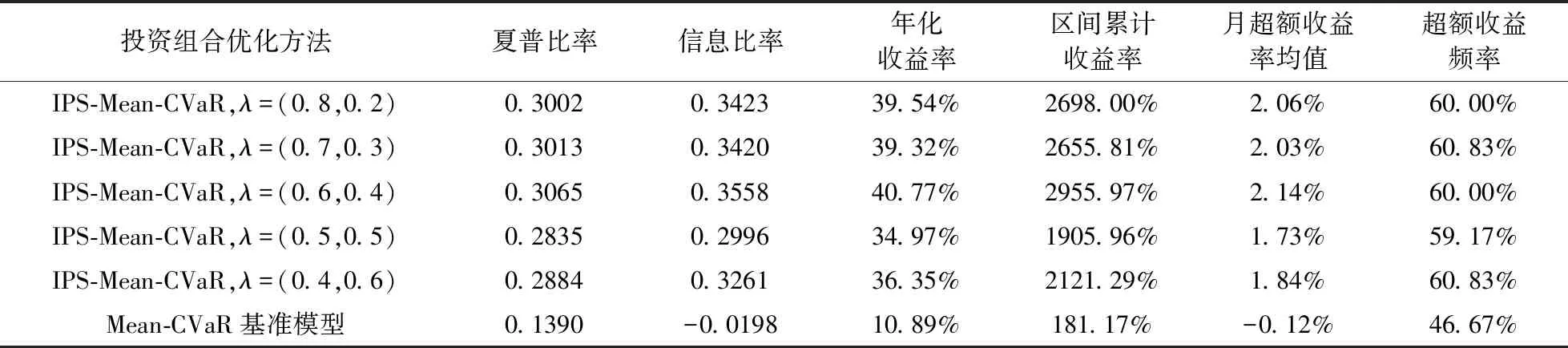
表3 IPS-均值-CVaR与CVaR基准模型的投资绩效对比

结果显示，IPS-均值-CVaR模型相对于CVaR基准模型，其优化投资组合在盈利性、风险收益比，以及跑赢市场基准概率上都得到了提高，各组投资组合累计收益走势如图3所示，前者表现出更加有效的资产配置优化能力和灵活性，因为可以适用于不同风险偏好的投资组合选择。值得注意的是，以上权重与投资组合表现在样本时间跨度上并未显示单调变化趋势。

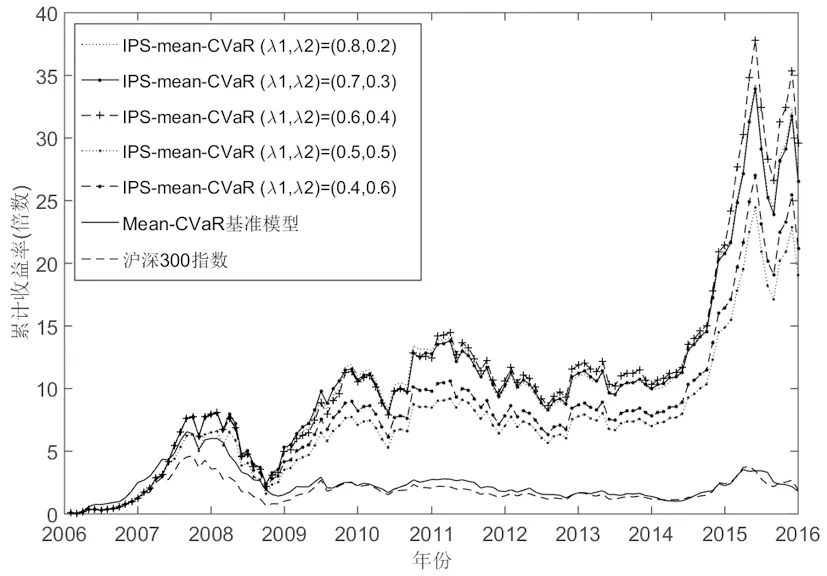
图3 IPS-均值-CVaR模型相对于均值-CVaR基准模型的优势

4 结论

本文基于投资理性应充分包含与收益率相关因子的假设，提出了有效因子选择、综合偏好强度(IPS)计算步骤，及IPS-Mean-CVaR投资组合选择模型。其创新与理论价值在于，在价值、动量、成长、规模、和分析师预测等多类别因子中，应用有效因子选择标准，选择对收益率表现显著影响的有效因子，融合形成风险-收益优化的附加理性，构建具有多因子是数据分析能力的投资组合选择模型。

通过沪深300成分股2006～2015年10年数据检验发现：

(1) 总市值、市盈率、市净率、市现率、净利润增长率、三个月动量以及一致预测EPS等七个因子，在沪深300成份股中表现为对收益率有显著影响的有效因子；其中，市盈率因子表现最突出，三个月动量(反转)因子表现次之，存在显著价值效益与中短期反转效应；

(2) 有效因子综合偏好强度构成的IPS投资组合，表现出比所有单因子投资组合的显著优势；和因子打分法对比，IPS方法也表现出更高的组合盈利和风险收益比，优于因子打分法；

(3) 有效因子IPS最大化作为附加目标，与基于风险-收益优化的均值-CVaR模型整合，在风险中性的有效投资组合上，收益率和风险收益比均优于IPS优选等权重组合；表明有效因子IPS最大化作为附加理性的IPS-Mean-CVaR模型具有信息增值作用。

投资分析模型的作用，在于将不断产生的数据转化为可用信息，提升投资理性和市场效率。就这个目的来说，投资者和市场对于模型的需求是没有止境的，沪深A股市场或许会有其阶段性特色，但不是例外。