基于双层博弈模型的民用航空产业链研究

王 博， 肖 刚， 肖 潇

(1.上海社会科学院 应用经济研究所,上海 200020; 2.上海交通大学 航空航天学院,上海 200240)

0 引言

由于大型客机的研发成本高、风险大，盈利周期长，大型客机制造业具有极高的进入壁垒，长期以来形成了波音公司与空中客车公司的双寡头市场格局。中国商飞自主开发的C919大型客机在浦东机场实现首飞，ARJ21成功获得量产证，都标志着我国大飞机研发和生产能力达到一个新的高度，未来我国民机产业对市场格局的影响也将会逐步显现。本文旨在利用经济学理论中的双层博弈模型，研究未来民机产业链格局的变化，预测商飞在定价、市场份额及关键零部件供应等环节对于双寡头垄断程度的影响；同时应用双层博弈均衡的概念，分析民机市场均衡对于潜在制造商的敏感度。

以往学者对民用客机制造业的研究主要聚焦于供应链：王彧和王季云认为民用航空制造业属于无分销环节的订单拉动式供应链，需要进行标准化来提高效率，并提出了标准化平台的设想[1]；李政则以波音787为实例，提出了波音公司这种主集成制造商与模块供应商的多层供应链的形成，并研究全球供应链的风险和对策，指出全球供应链模式能够利用全球资源分担风险，并可以提高反应效率，获得外包的市场，但同时也增加了总装风险、管理难度和协同失误可能性[2]。

文献中面对大型民用飞机制造商竞争的研究主要以双寡头垄断模型为主。其中Irwin和Pavcnik使用线性回归的方法估计出宽体客机市场需求份额和价格的关系，并在Bertrand和Cournot这两种竞争模型下估计出飞机制造公司的均衡利润[3]。Maria等学者则针对空客和波音两家公司在宽体远程客机市场上的竞争，通过对技术因素的分析，讨论了在不同博弈中(Bertrand和Cournot)的策略联盟和转移支付等行为[4]。Garcia的研究建立在简单纳什—古诺(Nash-Cournot)双寡头竞争模型的假设下，波音作为R&D的领导者，空客作为R&D的跟随者，通过向后归纳法得出各种影响对R&D项目补贴的激励因素[5]。这些学者的研究均重点关注飞机制造市场均衡和市场内企业竞争，但没有考虑飞机制造市场对供应商的影响。

和与以上文献不同，本文将从供应链角度出发，对民机制造市场的上下游企业以及潜在制造商的市场行为进行研究，同时将寡头博弈模型和供应链理论结合，采用Zhang和Lin[6]提出的分布式迭代算法，对于我国民机产业发展对市场结构的影响进行分析性预测。

其中本文将通过算例讨论，我国民机产业量化生产能力实现后，原有双寡头垄断市场的变化，各个企业的价格策略及对应的市场份额变化，并研究其对上游供应商的影响。

1 假设和模型描述

1.1 符号说明

α：飞机的基本市场价格；β：飞机制造商对飞机价格的敏感系数的倒数；i=1,2,…,n：飞机制造商索引；j=1,2,…,m：发动机制造商索引；αij：飞机发动机的基本市场价格；βij：飞机制造商i对发动机制造商j所生产的发动机的敏感系数的倒数；Qi：第i个飞机制造商的产量；P：飞机的市场价格；dij：飞机制造商i决定向发动机制造商j的发动机采购量；pij：飞机制造商i对发动机制造商j的发动机采购价格；qij：发动机制造商j决定给飞机制造商i的供应量；φij：发动机制造商j对飞机制造商i的供应量与其采购量不符的惩罚因子；Mi：飞机除采购发动机以外的基本采购及制造成本；Ni：飞机制造商对采购及制造飞机的敏感系数的倒数；cij：发动机制造商j为飞机制造商i制造发动机的成本；mij：发动机的基本市场成本；nij：发动机制造商j为飞机制造商i生产发动机的学习能力；capj：发动机制造商j的最大产能；σ：飞机制造商之间的价格比。

1.2 模型假设

考虑市场上存在i个飞机制造商，各自决定其产量Q，为简化模型，假设任意制造商i只生产一种机型且不同制造商的产品是完全替代的，飞机的市场价格由以下需求价格函数决定：

(1)

飞机发动机市场上存在j个制造商，假设任意发动机制造商j均有能力为任意飞机机型生产发动机，但是不同机型的发动机之间是不可替代的，此外不同发动机制造商为同一机型飞机所生产的发动机之间也是不同质的。

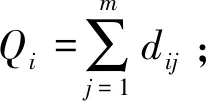
pij(dij)=αij-βij×dij
(i=1,2,…,n;j=1,2,…,m)

(2)

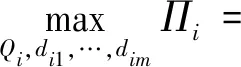
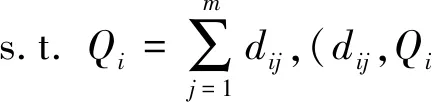
(3)

其中，目标函数中Mi-Ni×Qi表示除发动机采购以外的飞机制造成本。

假设发动机制造商j具有产能约束，且为飞机制造商i制造发动机的成本为：

cij(qij)=mij-nij×qij,
(i=1,2,…,n;j=1,2,…,m)

(4)

发动机制造商j的决策问题为：

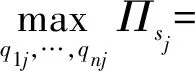
(5)

2 模型求解

根据斯塔克尔伯格(Stackelberg)博弈推导法，在飞机制造商主导的条件下，首先分析博弈下层发动机制造商确定对飞机制造商的供应量最大化自身利润；然后分析飞机制造商的最优产量和采购量，由此可得定理1～2。

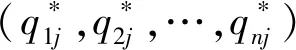
证明由式(5)已知发动机制造商的目标利润函数，将其利润最大化问题转换为KKT条件，为产能约束引入约束系数。

对于发动机制造商j，定义拉格朗日函数Lj(q1j,…,qnj,μj)，表达式如下：

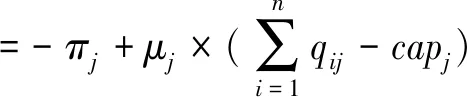
(6)

则发动机制造商j对飞机制造商的最优供应量应满足KKT条件，对拉格朗日函数Lj(q1j,…,qnj,μj)求一阶偏导数有：

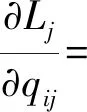
+mij+μj=0,(i=1,2,…,n)

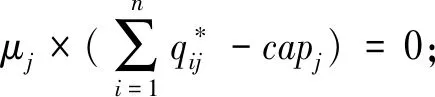
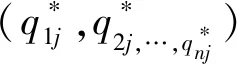
定理2在分散决策的情况下，飞机制造商的利润最大化问题可以转化成如下问题：

(Mi-Ni×Qi)×Qi

于是下层发动机制造商利润最大化问题的条件可以转化成上层飞机制造商利润最大化决策的约束，证毕。

该问题的算法如下：

Step 0设置初始的Xi(i=1,2,…,n),ε。Step 1将X-i(i=1,2,…,n)分别带入定理2的条件中,可对应求解得出X∗i。Step 2比较X∗i与Xi(i=1,2,…,n),如果∀i,有|X∗i-Xi|⩽ε,算法终止;否则令Xi=X∗i(i=1,2,…,n),返回Step 1。

3 结果分析

首先考虑目前波音、空客的双寡头竞争格局，即飞机制造商的数量为2且发动机制造商也有2家时的情况，借此来验证模型的合理性，在此基础上考虑C919量产后博弈均衡的变化情况，最后分析新进入的飞机制造商在不同市场行为下对自身决策的影响。

3.1 双寡头竞争模型

选取目前市场中的主流机型空客A320、波音737- 800作为研究对象，试验参数根据波音和空客的2016年度公司财务报表和生产交易数据及发动机供应商CFM、IAE的财务报告整理得出，时间段选取为一个季度。参数的具体数据见表1，程序运行结果为表2。

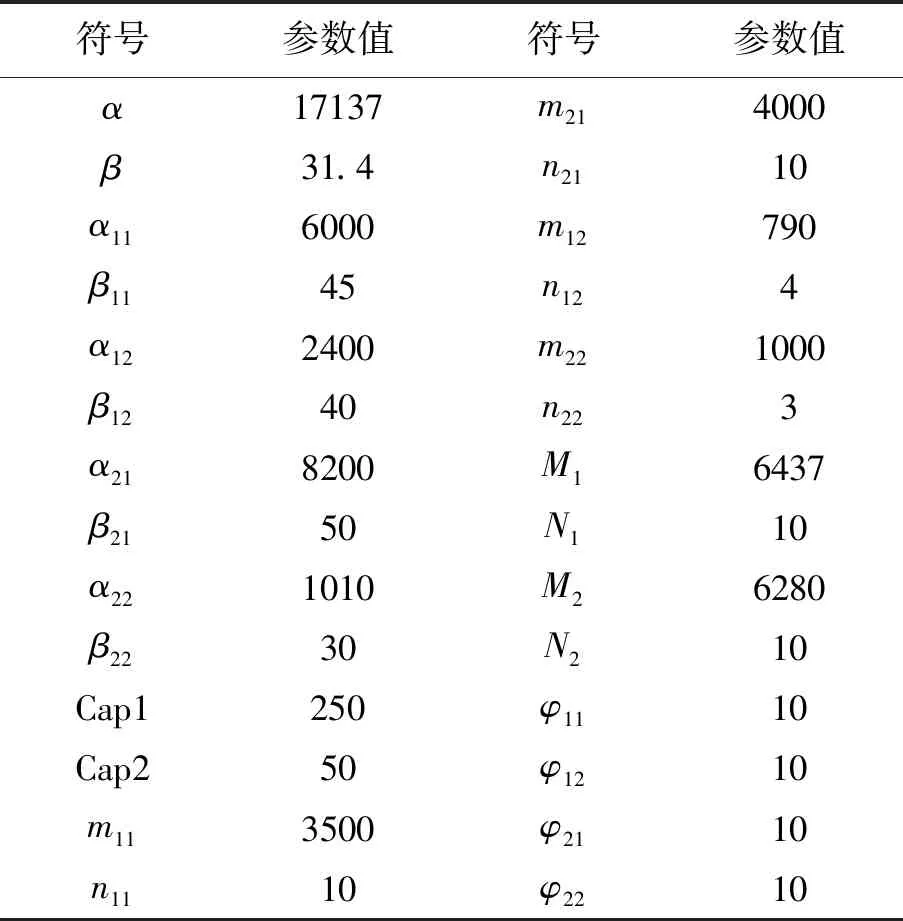
表1 双寡头竞争模型算例分析的参数表

(价格的单位为万美元，飞机的数量单位为一架，发动机的数量单位为一套。第一家飞机制造商为空客，第二家飞机制造商为波音，第一家发动机制造商为CFM公司，第二家发动机制造商为IAE公司。)

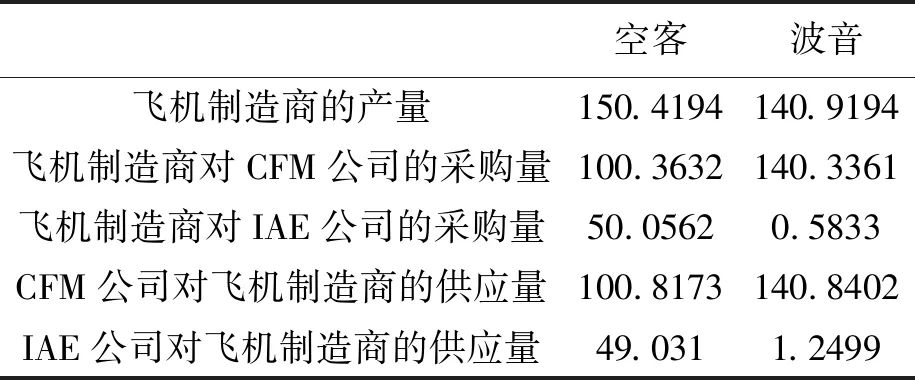
表2 双寡头竞争模型算例分析的结果表

计算结果显示：两家飞机制造商产量(150.4194，141.9194)与实际情况(150，140)基本相符，而发动机制造商对飞机制造商的供应量为(100.8173，49.0310)和(140.8402，1.2499)与实际情况(100,50)和(140,0)基本相符，说明模型的合理性。

3.2 三寡头竞争模型

选取目前市场中的主流机型空客A320、波音737-800以及中国商飞的C919作为研究对象，试验参数根据波音和空客的2016年度公司财务报表和生产交易数据，商飞已有的交易数据和C919有关的参数及发动机供应商CFM、IAE的财务报告整理得出，时间段选取为一个季度。参数的具体数据见表3，程序运行结果为表4。

由程序结果可以看出，C919正式进入市场以后，波音和空客的产量均有所下降。中国商飞每季度的产量约为62架，对CFM公司的采购量为62架，而对IAE公司的采购量为0架。CFM公司对商飞的供应量也达到了60架，与采购量相差不大，但是IAE公司对商飞的供应量约为17架，都是来自于原本IAE对空客的供应量，对此可能的解释是IAE预留出了对C919的产能。而对于波音和空客来说，除了产量的下降，另外的变化在于采购量和供应量之间的差额变大了，原因可能在于C919的出现抢占了发动机制造商的供应份额。

表3 三寡头竞争模型算例分析的参数表

(价格的单位为万美元，飞机的数量单位为一架，发动机的数量单位为一套。第一家飞机制造商为空客，第二家飞机制造商为波音，第三家飞机制造商为商飞，第一家发动机制造商为CFM公司，第二家发动机制造商为IAE公司。)

表4 三寡头竞争模型算例分析的结果表

在进行三寡头竞争模型的分析时，由于中国商飞的C919尚未进行量产化，算例分析中采用的也是商飞已有的交易数据而非商飞真正作为寡头出现的情况。因此我们对三寡头竞争模型作进一步的讨论。

研究对象仍是空客A320、波音737-800以及中国商飞的C919。由于前面的分析中并不是商飞真正作为寡头出现的情况，那么商飞对发动机制造商所生产的发动机的敏感系数会降低，倒数会增高，同时发动机制造商为商飞生产发动机的学习能力会降低，而波音和空客也会发生相应的改变。不妨将关于波音和空客的参数不变，对商飞的参数进行调整，同时将发动机制造商的产能扩大，时间段选取仍为一个季度。参数的具体数据见表5，程序运行结果为表6。

表5 三寡头竞争模型进一步讨论的参数表

(价格的单位为万美元，飞机的数量单位为一架，发动机的数量单位为一套。第一家飞机制造商为空客，第二家飞机制造商为波音，第三家飞机制造商为商飞，第一家发动机制造商为CFM公司，第二家发动机制造商为IAE公司。)

与之前的三寡头竞争模型的结果对比上来说，中国商飞真正作为寡头出现以后，空客的交易数据并没有受到影响，而波音的产量则会上涨，其采购量和供应量也随之上涨，而商飞的产量、采购量和供应量都大幅上涨。对此，可能的解释在于，与商飞一样都是CFM公司供应发动机的波音公司会受到商飞的影响，而其产量上涨的部分是来自发动机制造商产能的扩大，但大部分扩大的产能是提供给了中国商飞。同时可以看到，当对参数进行调整后，新的寡头中国商飞的市场份额会上升，而另外两个竞争对手波音和空客的份额则会相对下降。

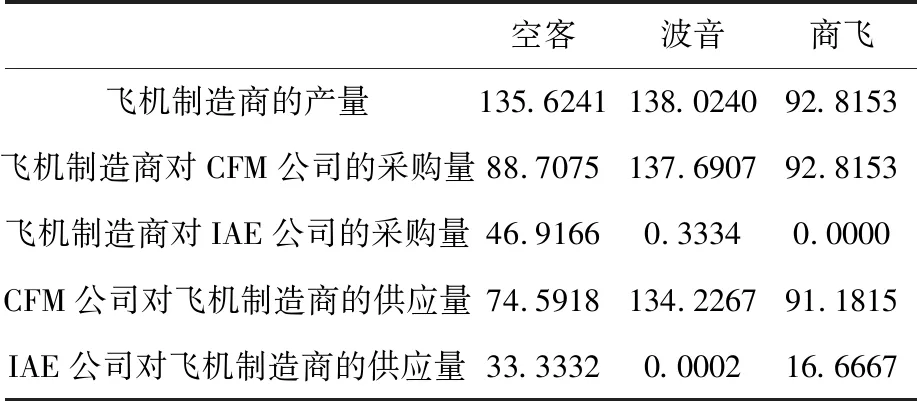
表6 关于三寡头竞争模型进一步讨论的结果表

3.3 C919的定价模型

根据上节结果，模型预计中国商飞每季度产量约为62架，所占市场份额约为19%，此时大飞机市场上价格为6838万美元，这个价格是偏低的。接下来考虑，如果C919的定价和737-800以及A320是不一样的，那最后它所份额会是怎样。假设C919作为新进入市场的大飞机，其定价与竞争产品相比会较低，其他假设不改变，则空客和波音所生产的飞机的市场价格为:

P(Q1,Q2,Q3)=α-β×(Q1+Q2+σ×Q3)

(7)

其中Q1，Q2，Q3分别为空客，波音和商飞的产量，而σ为C919与竞争产品的价格比，则C919的市场价格为：

P′(Q1,Q2,Q3)=σ×P(Q1,Q2,Q3)

σ×(α-β×(Q1+Q2+σ×Q3))

(8)

根据(7)、(8)式，来分析当三寡头竞争模型达到均衡时，C919的价格对产量和市场份额的影响。程序与上节一致，通过调整价格比，得到结果如图1所示。

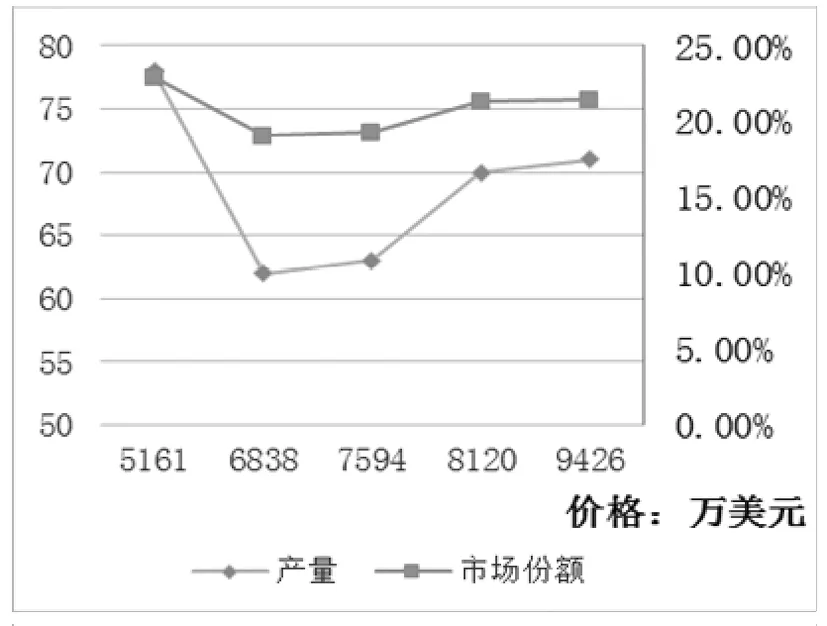
图1 C919的价格对产量和市场份额的影响

当价格比σ为0.8时，C919实际定价为5161万美元，每季度产量为78，市场份额最高，可达到22.94%。可以看到此时的定价是低于当σ=1时的6838万美元的，但是市场份额却是最高，可能得到的启示是C919刚进入市场时可以采取低定价的策略，来抢占市场份额，随后则可以将定价维持在较高的水平，而市场份额也会有约20%。但是这里的分析都只是静态的，其他寡头的定价策略也会改变，对产量和市场份额的影响也会不同，因此动态的定价过程将是进一步要研究的工作。

4 结论

本文在大飞机寡头市场中，利用双层博弈模型，研究了飞机制造商与发动机制造商的决策问题，并讨论了飞机制造商由双寡头变成三寡头时对整个双层博弈的影响以及新进入的飞机制造商的市场行为对其市场份额的影响。本文主要的工作在于首先建立了一个双层博弈的模型，下层博弈得出的条件可以作为上层的约束，在此基础上讨论了飞机制造商与发动机制造商之间的最优决策。然后本文对此模型设计算法，建立程序，得到关于模型的可行解，并对其进行分析和讨论。最后本文讨论了C919的定价问题，在价格为5161万美元时，市场份额最高约为23%。

本文虽然讨论了飞机制造商与发动机制造商之间的博弈决策问题，但还存在一些不足和有待进一步研究的方向。首先本文假设飞机是完全可替代的，市场价格是一致的，没有考虑到产品替代率的问题。其次本文假设的价格函数和成本函数都为线性函数，可能存在与实际不符的情况。此外动态的定价模型也可以是后面继续研究的方向。